基于小波脊的自适应傅里叶变换包裹相位滤波技术

张伟，王红霞，任爱华，孙国兴

（湖北汽车工业学院 机械工程学院，湖北 十堰 442002）

基于小波脊的自适应傅里叶变换包裹相位滤波技术

张伟，王红霞，任爱华，孙国兴

（湖北汽车工业学院 机械工程学院，湖北 十堰 442002）

应用小波变换法提取变形条纹小波脊的相位信息并获得全场包裹相位，并采用窗口傅立叶变换对包裹相位图进行滤波。在滤波过程中，通过调节小波脊参数来调整滤波窗口的大小，使窗口大小与变形条纹频率相匹配，从而提高包裹相位图滤波的效率和质量，获得较高质量的包裹相位图。实验结果表明：本方法有效提高了条纹图解包质量和效率，获得了较高的测量精度。

滤波；小波变换；窗口傅立叶变换

Abstract:The wrapped phase map was extracted from a fringe pattern by using wavelet transform and filtered by Window Fourier Transform(WFT).In the processing of filtering the wrapped phase map,the size of the filtering-window used to match the deformed fringe,s local frequency,was adjusted by the wavelet ridge parameters.The time of filtering wrapped phase map was reduced and the quality of the wrapped phase map was improved.The result shows that the proposed method has a higher quality and efficiency of unwrapping wrapped phase maps,and a higher accuracy of measurement.

Key words:filtering;wavelet analysis;Windowed Fourier Transform

光栅投影三维非接触光学测量广泛应用于工业测量、形貌检测、逆向工程、微电子封装检测等领域［1-3］。在光栅投影测量中，物体表面形状导致投射到物体表面上的正弦光栅被调制变形，利用CCD获得物体表面的变形光栅条纹图像，通过特定算法提取出包含物体表面形状信息的相位，进而获得被测量物体表面三维形状信息［4-6］。目前，较为常用的相位提取方法有需要多幅变形条纹图的相移法和只需要单幅变形条纹图的傅立叶变换法、小波变换法等［7-10］。其中小波变化法具有多分辨率分析的特性，通过小波变化处理既能够得到信号整体特征，又能够对局部信号的细节进行分析，具有较好的时间/空间局部性［11-12］。实践中采用小波变换求解条纹图像的相位，解决了傅里叶变换中的频谱混叠问题，进而可获得更高的测量精度。

利用小波变换分析变形条纹图，提取出小波脊处的相位信息，最终得到全场条纹图的相位分布信息，即包裹相位图。由于得到的是2π截断相位，需要进行相位展开，最终获得完整的三维形状信息［13］。包裹相位图的质量决定着相位展开过程中的误差传递以及最终的测量精度，因此在实际测量中，从变形条纹图提取包裹相位图及对包裹相位图进行相位展开往往采用图像滤波来提高图像质量。

文中采用小波变换方法从变形条纹图中提取相位信息，并进一步应用小波脊参数调节变换窗口的宽度来适应条纹局部的变化，采用窗口傅立叶变换对包裹相位图滤波以改善图像质量，提高测量效率和测量精度。

1 条纹图相位提取

一般获取的变形条纹图像I(x,y)可以表示为

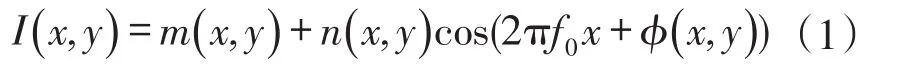
式中：m(x,y)为背景光强；n(x,y)为物面反射率；f0为光栅频率；ϕ(x,y)为物面高度调制的相位。I(x,y)条纹图任一行为f(x)，设母小波函数为

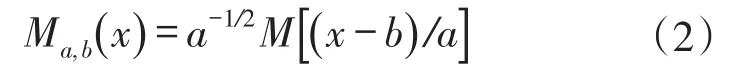
式中：a为尺度因子，a＞0；b为平移因子，b∈R。a可对母小波函数M(x)做伸缩，a愈大M(x/a)愈宽，反之亦然。即当a较大时空域分辨率较低，频域分辨率较高；当a较小时空域分辨率较高，频域分辨率较低。经过不同尺度因子a伸缩和平移因子b平移后的函数Ma,b(x)的复共轭函数可以表示为。则对f(x)作一维连续小波变换，其中一维连续小波变换为

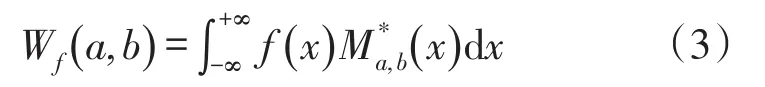
则小波系数的幅值A(a,b)与相位ϕ(a,b)为

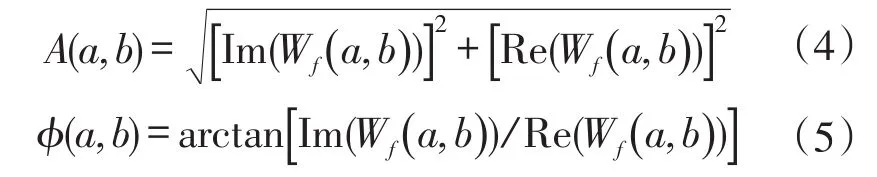
该函数f(x)连续小波变换，由式（2）描述了该函数与小波序列的内积关系，以（a，b）为参数的幅值及相位反映了该函数与小波序列函数的相似程度。当该函数的局部频率与相应尺度的小波函数振荡频率相同或者相近时，其小波变换系数幅值相应较大。其中，在各个位置沿尺度轴方向上，小波变换系数幅值最大值的位置连线定义为小波变换脊（wavalet ridge）［14］，进而提取小波脊处所对应的相位值，得到含有物体高度信息的调制相位，即相对相位分布在[0,2π]的包裹相位。

式中：arb为平移因子b对应的小波脊处尺度因子。最终获得条纹图f(x)的包裹相位图ϕ(x)。

2 包裹相位图滤波

实际测量中，受到噪声、阴影、不连续等影响，条纹图及对应包裹相位图也会受到噪声等影响。一般采用速度较快的均值滤波和中值滤波处理，但滤波效果一般，会降低相位图空间分辨率，模糊条纹边缘。对于包裹相位图的滤波去噪，目前较为典型的滤波处理是采用正余弦滤波、窗口傅立叶滤波［15］。其中窗口傅立叶变换滤波处理过程中，具有较好的局部属性，能够有效降低区域强噪声，同时降低非有效数据的误差传播，但是计算时间较慢。

窗口傅立叶滤波基本原理是将包裹相位主值的反正切函数分解为sin(ϕ(x))和cos(ϕ(x))两部分，避免直接对截断相位滤波处理，则对包裹相位图像函数任一行fw(x)进行指数化处理，将包裹相位主值映射到复平面，则

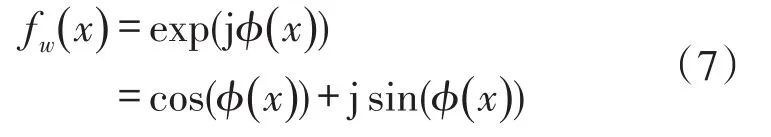
对包裹相位图像进行窗口傅立叶变换为

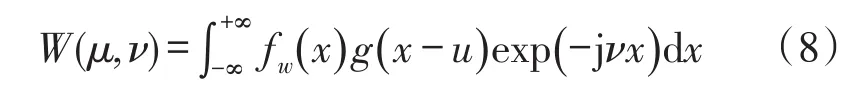
式中：g(x)为高斯窗口函数，g(x)=exp(-x2/2δ2)；参数δ控制高斯窗口的大小。通过变换式（8）为

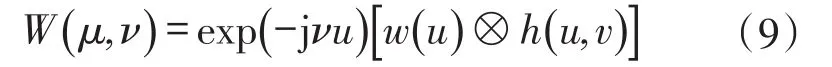
式中：h(u,v)=g(u)exp(jvu)，⊗为卷积。对W(μ,ν)滤波处理，thr为滤波阀值，则

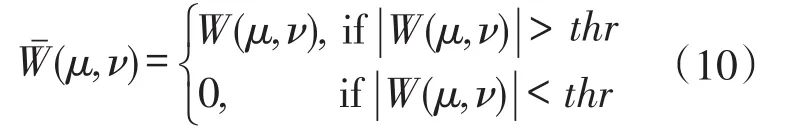
被测表面形状对条纹调制结果是：形状变换较大的位置对应的变形条纹密集，反之变形条纹分布稀疏。根据前述变形条纹图小波变换分析，小波系数幅值反映了变形条纹图局部频率，即小波系数幅值对应了变形条纹密集系数分布情况。同时包裹相位图中相位跳变频率与条纹图条纹频率是一致的，因此条纹图小波脊参数也反映了包裹相位图相位跳变频率。

采用在空域和频域都具有很好局部化性能的Morlet复小波函数作为母小波，对变形条纹图进行处理，获得包裹相位图。Morlet复小波函数为

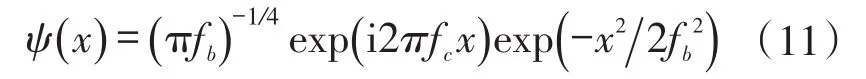
式中：fb为小波函数带宽；fc为小波中心频率与变形条纹图中条纹基频一致。

根据前述小波脊参数与包裹相位图相位跳变频率的关系，尺度轴方向上小波脊所对应的伸缩因子a即能够适应不同频率最佳匹配窗口宽度，则窗函数通过伸缩平移得到窗函数族：

该窗口函数中心为以b为中心，窗口随b移动，窗口随着a值由小变大变化而由窄变宽。从而得到一个可调的空间——频率窗：

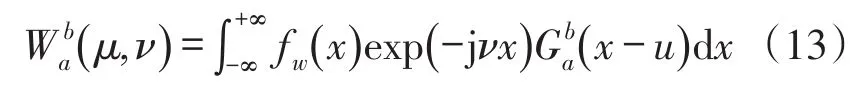
由高斯函数性质：

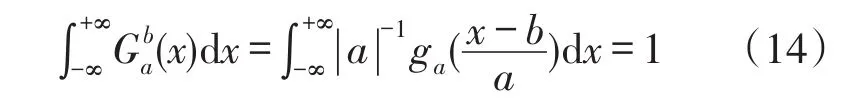
窗口可调傅里叶变换得到的频谱叠加起来与傅里叶变换的频谱是一致的。

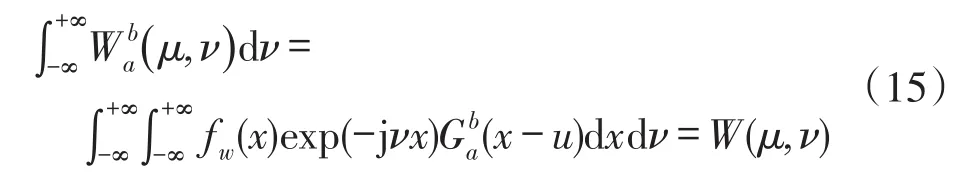
3 包裹相位实验分析

为验证基于小波脊参数控制的傅立叶变换窗口对包裹相位图的滤波质量和效率，对模拟物体（图1）进行滤波分析，模拟物体对应函数为式（16），其变形条纹图为图2，分析并加入噪声得到图3及其对应的带有噪声的变形光栅条纹（图4）。

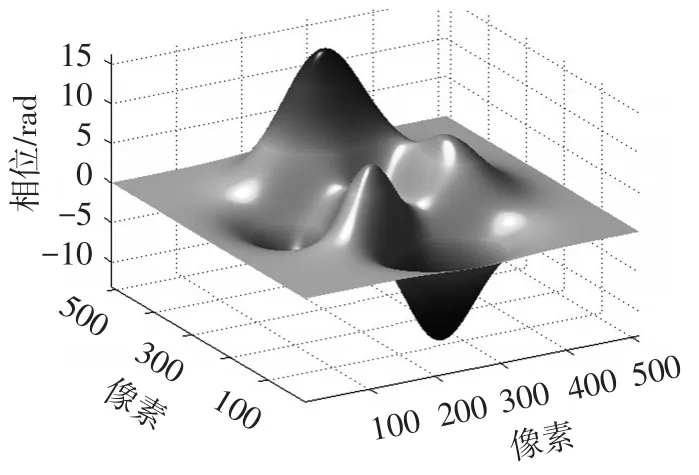
图1 模拟物体

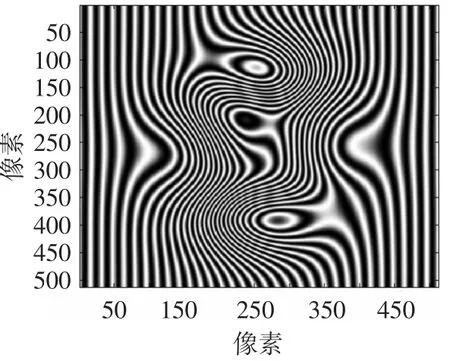
图2 模拟物体图1的变形条纹图

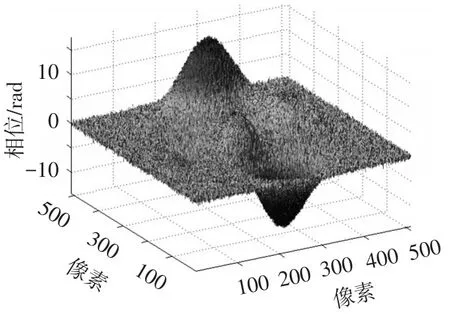
图3 对图1加入随机噪声

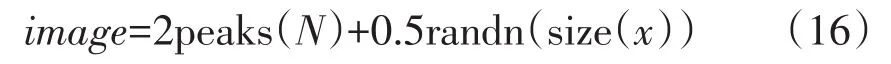
式中：image为模拟物体加入标准差为0.5的高斯噪声。

为了降低相位信息的丢失率，没有对光栅条纹图进行滤波预处理，而是通过小波变换获得包裹相位图（图5）。作为对比，给出了没有噪声影响的包裹相位图（图6）。采用Itoh解包算法对噪声污染的包裹相位图进行解包，结果如图7所示出现局部解包错误，并且解包结果噪声较大。

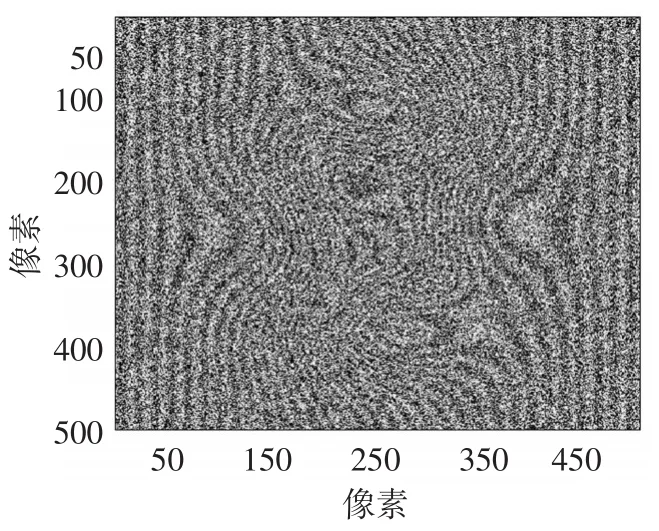
图4 加入噪声后图3的变形条纹图

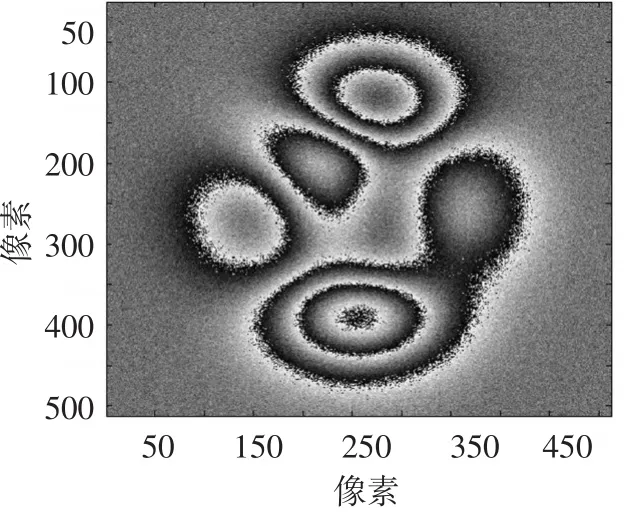
图5 对应图3的包裹相位图

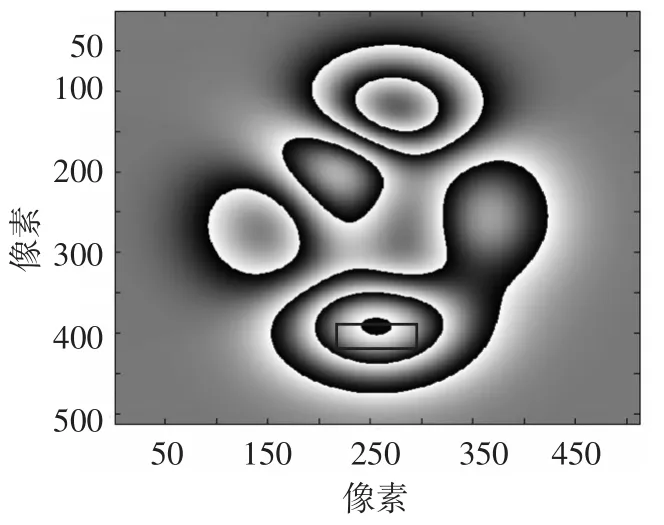
图6 对应图2的包裹相位图

采用窗口傅立叶变换滤波对噪声包裹相位图（图5）进行滤波处理，滤波后的结果如图8所示，对比图6，发现在图中红色线框处窗口傅立叶变换滤波处理导致相位跳变发生丢失，而采用自适应窗口傅立叶变换滤波获得滤波包裹相位图如图9所示，其与图6几乎是一致，没有出现包裹相位图滤波后相位跳变丢失情况，可见自适应窗口具有更好的局部频率适应性。对图9进行解包恢复物体三维高度（图10），结果较为平滑，没有出现解包错误或者解包不能。与原始物体高度图1对比，得到图11所示的高度误差结果，其最大误差为0.05 rad，结果表明自适应窗口傅立叶变换滤波能够有效提高测量精度。同时，在相同的计算平台（Matlab）下，自适应窗口傅立叶变换滤波时间为23 s，窗口傅立叶变换滤波处理计算时间为66 s。对比表明自适应窗口傅立叶变换对包裹相位具有更高的滤波效率。

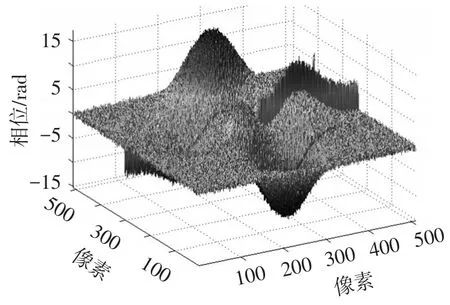
图7 用Itoh算法解包图6的错误结果

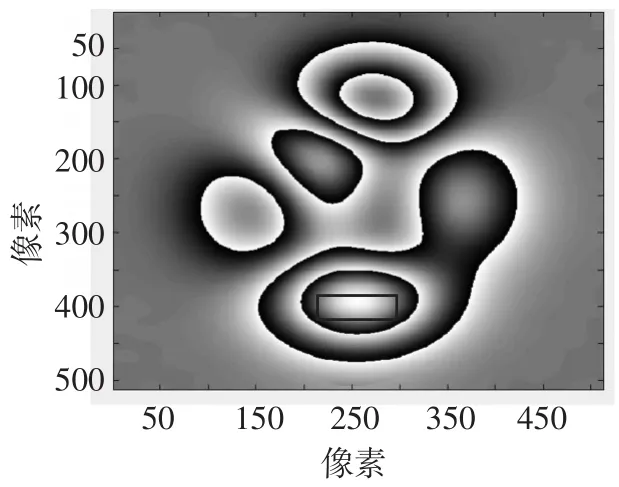
图8 窗口傅立叶变换滤波

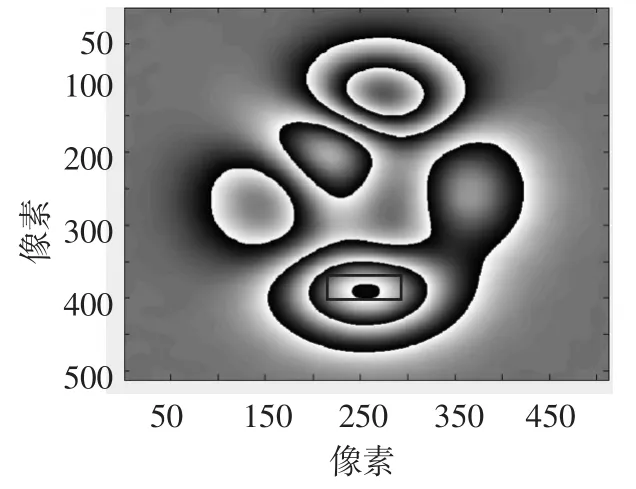
图9 自适应窗口傅立叶变换滤波

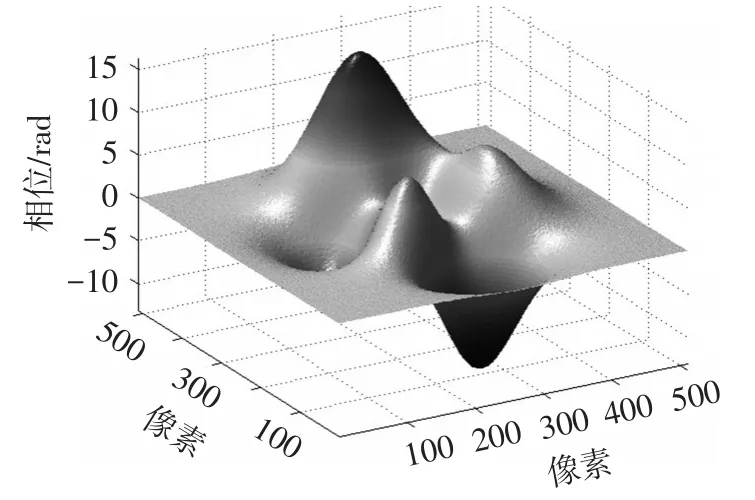
图10 对图9解包得到物体三维高度结果

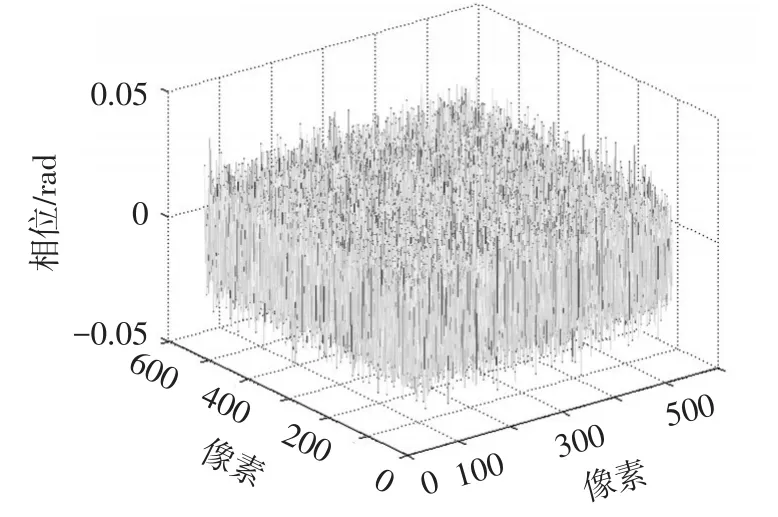
图11 物体高度与图10之间高度误差

4 结论

在小波变换提取包裹相位图基础上，充分应用小波脊参数控制窗口傅立叶变换滤波的滤波窗口，以适应包裹相位图中不同相位跳变密度，有效地提高了对包裹相位图噪声滤波质量和滤波速度。在同样的计算平台下，基于小波脊参数控制的自适应傅立叶变换窗口的滤波效率和质量明显高于传统的窗口傅立叶变换对包裹相位图的滤波。

［1］Li D,J Kofman.Adaptive Fringe-pattern Projection for Image Saturation Avoidance in 3D Surface-shape Mea⁃surement［J］.Optics Express，2014,22（8）：9887.

［2］Chen K，Xi J，Yu Y，et al.Three-dimensional Measure⁃ment of Object Surfaces with Complex Shape and Color Distribution Based on Projection of Color Fringe Patterns［J］.Appl Opt，2013,52（30）：7360-6.

［3］戴士杰，邵猛，王志平，等.钛合金叶片三维测量中背景去除的两步法研究［J］.光电子-激光，2014（08）：1540-1547.

［4］肖志勇.基于数字投影的三维形貌测量系统的实现［J］.通信技术，2011（2）：112-114.

［5］丁明君，牛萍娟，李寅涛.光栅投影三维形貌测量方法及发展趋势研究［J］.光机电信息，2008（9）：31-36.

［6］Quan C，Tay C J,Huang Y H.3-D Deformation Measure⁃ment Using Fringe Projection and Digital Image Correla⁃tion［J］.Optik，2004,115（4）：164-168.

［7］黄柏圣，许家栋.基于短时傅里叶变换的干涉相位解缠方法［J］.现代雷达，2009（9）：55-58.

［8］杨锋涛，罗江龙，刘志强，等.相位展开的6种算法比较［J］.激光技术，2008（3）：323-326.

［9］Zhou S,Fu Y,Tang X,et al.Fourier-based Analysis of Moire Fringe Patterns of Superposed Gratings in Align⁃ment of Nanolithography［J］.Opt Express，2008,16（11）：7869-7880.

［10］Mutoh K,Takeda M.Fourier Transform Profilometry for The Automatic Measurement of 3-D Object Shapes［J］.Appl Opt,1983,22（24）：3977.

［11］Da F,Huang H.A fast,Accurate Phase Unwrapping Method for Wavelet-transform Profilometry［J］.Optics Communications,2012,285（4）：421-432.

［12］Cui S L，Li D H，Li Q G.Phase Retrieval from Fringe Pattern with 1-D Discrete Wavelet Transform［J］.Op⁃tics&Lasers in Engineering,2012，50（2）：268-279.

［13］Watkins L R.Review of Fringe Pattern Phase Recovery Using The 1-D and 2-D Continuous Wavelet Transforms［J］.Optics&Lasers in Engineering,2012,50（8）：1015-1022.

［14］李思坤，陈文静，苏显渝.小波变换轮廓术中用小波脊系数幅值引导相位展开的研究［J］.光学学报，2008（4）：715-721.

［15］Kemao Q，Wang H，Gao W.Windowed Fourier Trans⁃form for Fringe Pattern Analysis：Theoretical Analyses［J］.Applied Optics，2008，47（29）：5408.

Filtering Wrapped Phase Map with Adaptive Window Fourier Transform Based on Wavelet Ridge

Zhang Wei,Wang Hongxia,Ren Aihua,Sun Guoxing
（School of Mechanical Engineering,Hubei University of Automotive Technology,Shiyan 442002,China）

TN247；TP391.41

A

1008-5483（2017）03-0038-04

10.3969/j.issn.1008-5483.2017.03.010

2017-03-30

湖北省自然基金（2014CFB624）；湖北汽车工业学院博士科研启动基金项目（BK201602）

张伟（1977-），男，安徽蒙城人，副教授，博士，从事精密机械、精密测量方面的研究。E-mail：zhangwei7766@163.com