巴拿赫空间中斜演化半流的多项式三分性的2个刻画

岳田

（湖北汽车工业学院 理学院，湖北 十堰 442002）

巴拿赫空间中斜演化半流的多项式三分性的2个刻画

岳田

（湖北汽车工业学院 理学院，湖北 十堰 442002）

分别利用2个和4个投影族给出了巴拿赫空间中斜演化半流的多项式三分性的2个刻画。

巴拿赫空间；斜演化半流；多项式三分性

Abstract:Two characterizations for the polynomial trichotomy of skew-evolution semiflows in Banach spaces were given by means of two projection families and four projection families respectively.

Key words:Banach space;skew-evolution semiflows;polynomial trichotomy

近年来关于有限或无限维Banach空间中演化方程解的渐近行为（稳定性、膨胀性、二分性、三分性）研究取得了突破性的进展，获得了非常丰富的成果［1-10］。作为二分性的推广，三分性成了动力系统最为复杂的渐近性质之一，尤其在解决分歧理论中起着重要作用。关于三分性的概念首先由Sack⁃er和Sell引入［1］，接着Elaydi与Hajek给出了微分系统指数三分的概念［2-3］，随后关于三分性的研究获得了极大关注。如文献［4］研究了Banach空间中演化算子一致指数三分的充要条件；文献［5］给出了Banach空间中演化算子一致指数三分的等价定义；文献［6］利用斜积流对相应的动力系统的指数三分性及容许性进行了刻画。

由于斜演化半流在刻画动力系统的渐近行为方面比强连续算子半群、演化算子、斜积流更为合适，进而近年来对其研究较多［7-10］。因为指数型渐近行为的条件要求比较苛刻，对其适当弱化，则导致了多项式渐近行为的相关概念产生，如文献［10］对Banach空间中斜演化半流的一致多项式稳定性及一致多项式不稳定性的性质进行了研究。文中在上述文献的基础上，给出Banach空间中斜演化半流的多项式三分性的2个刻画。

1 预备知识

设(X,d)为一度量空间，V为一实或复的Ban⁃ach空间，B(V)为V上所有有界线性算子全体构成的集合。记I为V上的恒等算子，

定义1［7-8］映射φ:T×X→X称为X上的演化半流，如果满足

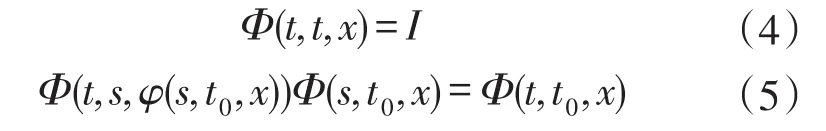
式中：∀t≥0，∀(t,s)，(s,t0)∈Δ；∀x∈X。

定义2［7-8］映射Φ:T×X→B(X)称为演化半流φ上的演化上循环，如果满足

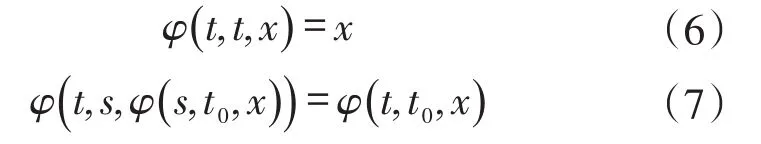
式中：∀(t,s),(s,t0)∈Δ，∀(t,x)∈R+×X，∀x∈X。

定义3［7-8］映射C:T×Y→Y，

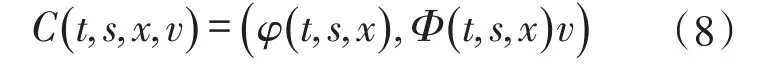
称为Y上的斜演化半流，其中Φ为演化半流φ上的演化上循环。

定义4［9］称映射P:X→B(V)为V上的投影族，如果满足P2(x)=P(x),∀x∈X。

定义5 称三投影族{Pi}i∈{1,2,3}与斜演化半流C=(φ,Φ)相容，如果满足

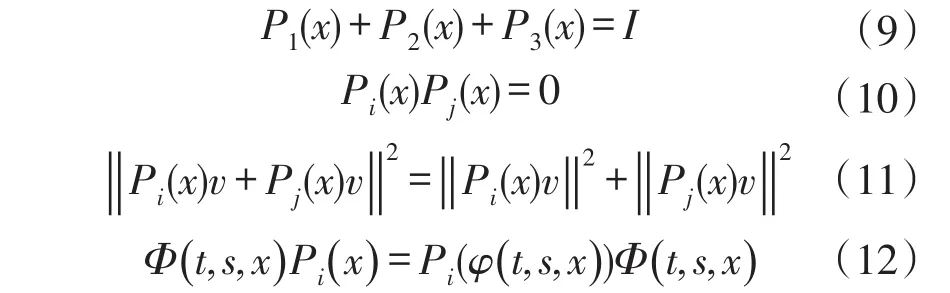
式中：∀x∈X，∀x∈X，∀i,j∈{1,2,3}，i≠j，∀(t,s,x)∈Δ×X，∀(x,v)∈Y。

定义6 称斜演化半流C=(φ,Φ)为多项式三分，如果存在常数α1,α2＞1，非减函数N:R+→[1,+∞)及3个与C相容的投影族{Pi}i∈{1,2,3}使得

对∀(t,s,r,x,v)∈Θ×Y成立。

2 主要结论

众所周知，多项式二分性是利用2个投影族来进行刻画，多项式三分性作为其推广。利用2个投影族来刻画斜演化半流的多项式三分性。

定义7 称投影族{Ri}i∈{1,2}与斜演化半流C=(φ,Φ)相容，如果满足

式中：∀x∈X,∀(x,v)∈Y,∀(t,s,x)∈Δ×X,∀i∈{1,2}。

定理1 斜演化半流C=(φ,Φ)是多项式三分的，当且仅当存在常数α1,α2＞1，非减函数N:R+→[1,+∞)及2个与C相容的投影族{Ri}i∈{1,2}使得

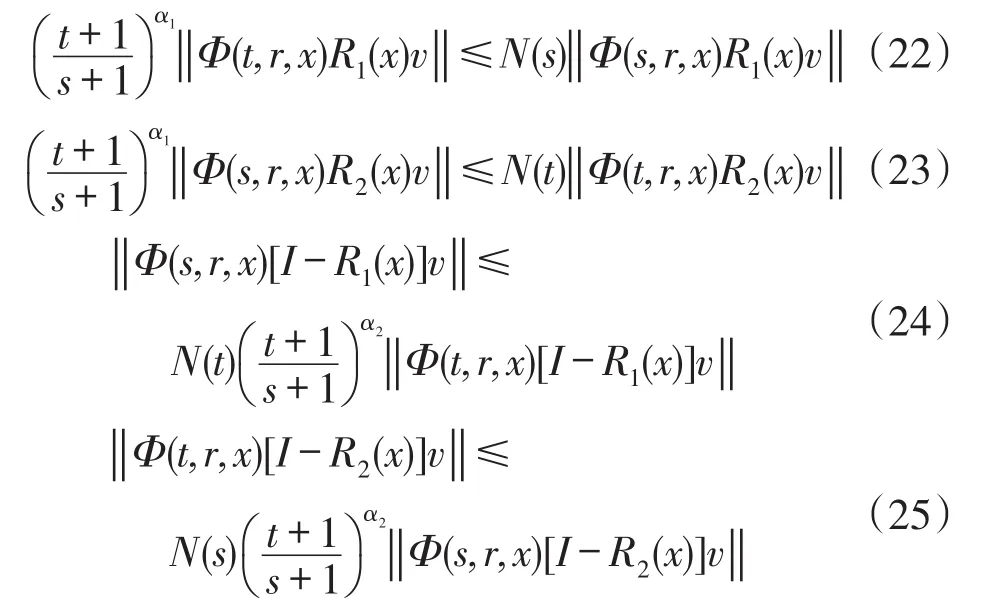
对∀(t,s,r,x,v)∈Θ×Y成立。

证明：必要性。令R1=P1，R2=P2。则由定义5中式（10）～（12）可知定义7中式（17）～（18）和式（21）成立。利用式（9）和式（11）可得

对∀(x,v)∈Y成立，即式（19）成立，类似可得式（20）成立。投影族R1,R2与斜演化半流C相容。

显然由定义6中式（13）～（14）可得式（22）～（23）。由式（11）～（12）和式（14）～（15）可得

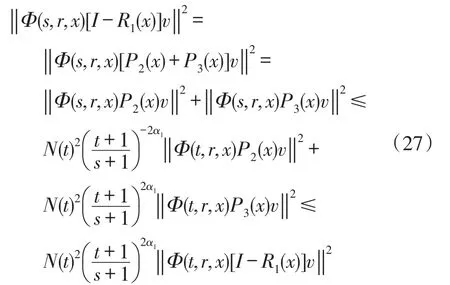
对∀(t,s,r,x,v)∈Θ×Y成立，即式（24）成立，类似可得式（25）。

充分性。令P1=R1,P2=R2,P3=I-R1-R2。则由式（17）～（21）可得式（9）～（12）成立。而且有（22）⇔（13），（23）⇔（14），下证式（15）。

由于P3=(I-R1)(I-R2)，利用式（24）得

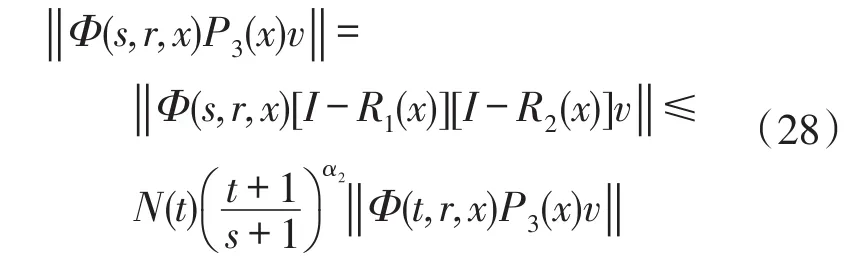
对∀(t,s,r,x,v)∈Θ×Y成立，即式（15）成立，类似可证式（16）。从而斜演化半流C是多项式三分的。

为了利用4个投影族来刻画斜演化半流的多项式三分性质，先给出定义8。

定义8 称投影族{Ti}i∈{1,2,3,4}与斜演化半流C=(φ,Φ)相容，如果满足如下条件：

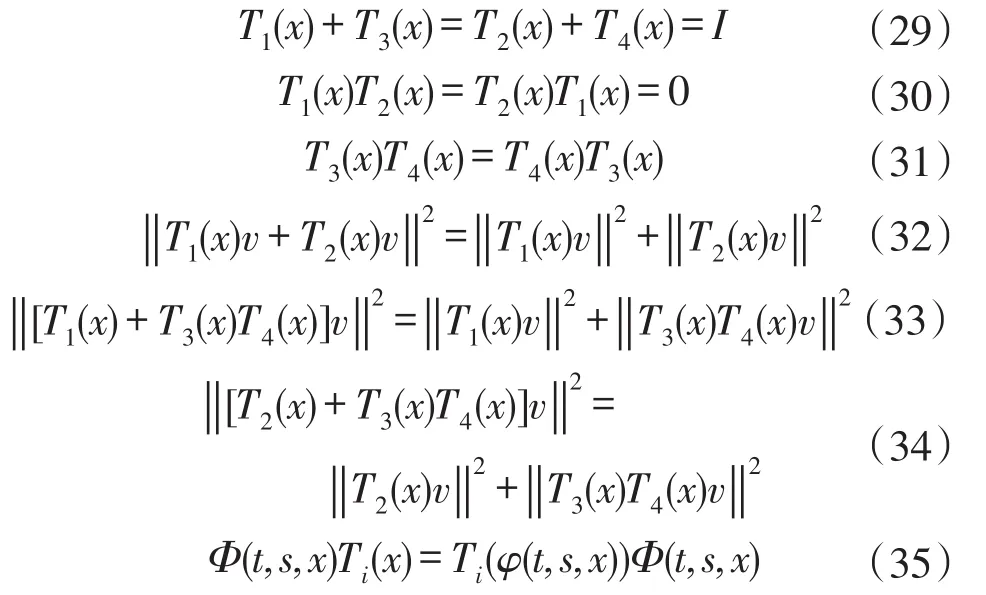
式中：∀(t,s,x)∈Δ×X，∀(x,v)∈Y，∀i∈{1,2,3,4}，∀x∈X。

定理2 斜演化半流C=(φ,Φ)是多项式三分的当且仅当存在常数α1,α2＞1，非减函数N:R+→[1,+∞)以及4个与C相容的投影族{Ti}i∈{1,2,3,4}使得

对∀(t,s,r,x,v)∈Θ×Y成立。

证明：类似定理1，此处略。

［1］Sacker R J，Sell G R.Existence of Dichotomies and In⁃variant Splittings for Linear Differential Systems,III［J］.Journal of Differential Equations，1976，22（2）：497-522.

［2］Elaydi S，Hajek O.Exponential Trichotomy of Differential Systems［J］.Journal of Mathematical Analysis&Applica⁃tions，1988，129（2）：362-374.

［3］Elaydi S，Hajek O.Exponential Dichotomy and Trichoto⁃my of Nonlinear Differential Equations［J］.Differential&Integral Equations，1990，3（6）：1201-1224.

［4］Megan M，Stoica C.On Uniform Exponential Trichotomy of Evolution Operators in Banach Spaces［J］.Integral Equations&Operator Theory，2008，64（4）：499-506.

［5］Megan M，Stoica C.Equivalent Definitions for Uniform Exponential Trichotomy of Evolution Operators in Banach Spaces［J］.Hot Topics Oper.Th.，2008，9（1），151-158.

［6］Sasu A L，Sasu B.Admissibility and Exponential Trichoto⁃my of Dynamical Systems Described by Skew-product Flows［J］.Journal of Differential Equations，2016，260（2）：1656-1689.

［7］Megan M，Stoica C.Exponential Instability of Skew-evo⁃lution Semiflows in Banach Spaces［J］.Stud.Univ.“Babes-Bolyai”Math.，2008，53（1）：17-24.

［8］Stoica C，Megan M.On Uniform Exponential Stability for Skew-evolution Semiflows on Banach Spaces［J］.Nolin⁃ear Analysis，2010，72（3）：1305-1313.

［9］Stoica C.Trichotomy for Dynamical Systems in Banach Spaces［J］.The Scientific World Journal，2013：Article ID 793813，1-8.

［10］岳田，雷国梁，宋晓秋.线性斜演化半流一致指数膨胀性的若干刻画［J］.数学进展，2016（3）：433-442.

Two Characterizations for the Polynomial Trichotomy of Skew-evolution Semiflows in Banach Spaces

Yue Tian
（SchoolofScience,HubeiUniversity ofAutomotive Technology,Shiyan 442002,China）

O177.2

A

1008-5483（2017）03-0059-03

10.3969/j.issn.1008-5483.2017.03.015

2017-02-28

湖北省自然科学基金（2014CFB629）；湖北汽车工业学院校预研基金（2014XY06）；湖北汽车工业学院本科教学建设与改革项目（JX201766）

岳田（1988-），男，四川南江人，助教，硕士，从事微分系统定性理论的研究。E-mail：ytcumt@163.com