一种点目标探测系统能量集中度计算方法
杨天远 周峰 行麦玲
一种点目标探测系统能量集中度计算方法
杨天远 周峰 行麦玲
(北京空间机电研究所,北京100094)
在点目标探测系统中,光学系统的能量集中度决定了单个像元收集到点目标能量的水平,直接影响点目标探测系统的图像信噪比。在相机设计完成后,需要对相机的能量集中度进行测试,评价相机的性能。传统方法对点目标探测系统的能量集中度计算采用“中心像元法”,由于相机探测器中心位置偏移和靶标尺寸的影响,计算结果存在很大误差。文章通过建立点源靶标成像模型,分析出靶标尺寸和探测器位置对点目标像斑的影响,提出了求解点目标能量集中度的一般过程,并设计出了一种容易实现的计算方法。通过对点目标像斑进行高斯拟合,然后通过两次反卷积去除探测器位置和靶标尺寸的影响,实现了对能量集中度的求解。计算结果表明,文中提出的方法比传统方法更接近实际情况,具有工程应用价值。
能量集中度 高斯拟合 反卷积 点目标探测 空间相机
0 引言
点目标的图像信噪比是评价点目标图像的主要参数。获得高而且稳定的图像信噪比是对点目标进行准确、高效、连续、稳定检出的必要条件[1-2]。在对点目标探测系统进行设计时,一般需要系统能够达到较高的能量集中度水平,从而使单个像元可以收集到大部分的目标能量[3-5]。对于同样的目标,能量集中度高的探测系统点目标像斑能量更高,可以获得更高的图像信噪比,系统对点目标的探测能力更强。
因此在点目标探测系统设计完成时,一般要对系统的能量集中度进行测试和计算,作为评价系统性能的依据。传统的计算方法从点目标像斑出发,以像斑中心像元的灰度值除以该像元与周围8邻域像元灰度值的总和来计算能量集中度,称之为“中心像元法”。由于在测试时使用的点源靶标有一定的尺寸,会影响计算结果,造成计算结果偏小;加之实际测量时无法做到中央像元的中心与点目标弥散斑完全重合,质心偏移导致计算结果偏小[6-9]。本文方法通过消除中心偏移和靶标尺寸的影响,降低了计算误差,相比于传统方法较为准确。
1 点源靶标成像建模
1.1 能量集中度定义
在很多情况下,为了方便计算,可以通过将光学系统的点扩散函数假设为高斯型来近似像差的总体效果,此时高斯型的点扩散函数对应的传递函数为高斯传递函数[10-11]

式中表示空间频率;为光学响应指数。
相应的点扩散函数(,)表达式为[12]

式中 (,)表示像面上一点的坐标。
本文中,能量集中度定义为点扩散函数弥散斑在一个像元中所包含的能量与总能量的比。对于像元尺寸为1×2的系统,能量集中度可以表示为[13]

可以看出,能量集中度为光学响应指数与像元尺寸的函数。
1.2 点源靶标像斑分布
在进行测试时,选用的孔型靶标由于有一定的尺寸,在像面上的理想辐射分布(,)为

式中T为目标辐照度;0为入瞳面积;0为相机焦距;、为靶标在方向和方向的尺寸;为靶标与相机间的距离。
实际弥散情况下靶标的能量分布(,)为理想辐射分布与点扩散函数的卷积

实际得到的靶标像斑为像元感光区域对靶标弥散斑能量积分结果,数学上表示为对矩形窗口(与感光面积对应)与靶标的能量分布的卷积结果进行离散采样,具体为
(6)
式中0,0为能量积分时探测器距原点最近单元的中心位置;(,)为像斑“源函数”,没有物理意义,表达式为

式中3、4为探测器像元感光区域在、方向的尺寸。
从点扩散函数到靶标像斑的数学建模过程如图1所示。

图1 靶标像斑建模过程
2 能量集中度求解方法
求解能量集中度的过程就是通过靶标像斑求得系统点扩散函数,然后对点扩散函数积分求解的过程。因此,需要将图1的过程逆过来,通过靶标像斑分布的离散像素拟合出靶标像斑的源函数,再通过两次反卷积求得点扩散函数。
在靶标尺寸较小时靶标像斑源函数分布与高斯分布相似。因此,在对靶标像斑进行拟合时,选用高斯函数[14],其表达式为

式中A、B、C、D、E都是拟合时需要确定的参数;是高斯基函数的个数。
采用高斯拟合后可以寻得靶标像斑源函数的峰值,从而消除了探测器相对位置的影响。
已知(,)通过式(7)求解(,)的过程为反卷积[15-19]。本文利用高斯函数和矩形窗口的特点,设计出一种容易实现的反卷积算法,以一维的情况进行说明。当矩形函数的长度为时,设()为需要通过反卷积求解的函数,()为()与矩形窗口的卷积,则()表达式为

在轴上任取两点1、2,当1、2间隔比较小时:
(10)
式中 Δ=2–1。
式(10)的表达式如图2所示。
从而得到

在计算中选择比较小的Δ值,即可得到比较高的精度。等式右侧是可以求得的,等式左侧可以看做数列(x+/2)中有一定间隔的两项的差。若求得数列的前/Δ项,利用叠加法便可以求得所有的(x+/2)。即求得了()的一系列离散值。那么如何求得数列前/Δ项呢?卷积结果在距原点较远时,能量非常小,可以将原点以左某一处的值近似为0,从这个点开始,每隔Δ取一个()的值,然后将这个值除以Δ,连续取/Δ项,就得到了数列的全部起始项。
图2 式(10)算法示意
Fig.2 Schematic diagram of formula(10)algorithm
实际情况是两维的,在两个方向上做两次这样的运算即可。完成两次反卷积后即可得到系统点扩散函数的分布情况,从而计算能量集中度的值。
3 试验验证
3.1 试验条件
试验设备如图3所示,在低温黑体前设置了孔型靶标模拟点源,通过平行光管和相机成像在焦平面上。相机探测波段为8~12μm,能量集中度设计值为0.5。相机探测器为面阵器件,单元尺寸为30μm×30μm,感光面积为24μm×24μm。平行光管焦距为3 210mm,相机焦距为450mm,靶标尺寸为90μm×90μm。测试时的靶标温度为110K,冷板温度为80K,探测器积分时间为120μs。

图3 点源靶标成像设备
可以按照下式计算得出靶标像方尺寸
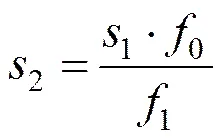
式中2为靶标像方尺寸;1为靶标尺寸;1为平行光管焦距。
计算得出靶标像方尺寸为12.6μm,靶标像方尺寸为探测器单元尺寸的42%,与理想点源存在差距,会给能量集中度的测试带来误差。
3.2 能量集中度计算
图4(a)、图4(b)为靶标的像斑原图和去除冷板背景后的图像。可以看出,靶标像斑能量分布不对称,说明靶标弥散斑中心与中央像元中心未对准,若按常规方法计算,会带来比较大的误差。

(a)靶标像斑原图
(a)Original image of the point source

(b)靶标像斑去除背景后图像
(1)常规方法
像斑能量分布矩阵(DN值)为

中心像元法计算能量集中度为
(13)
式中(,)表示中心像元的能量值。
计算得到的能量集中度为0.360 3,与相机的能量集中度设计值存在很大差距。
(2)本文方法
将像斑能量矩阵周围增加零元素,扩充为7×7的矩阵,并向最大值进行了归一化,在MATLAB环境下对像斑能量矩阵进行高斯拟合。在拟合中发现,选用一个高斯基函数即可得到比较高的精度。得到的式(8)的拟合系数为=1.058,==1.092,=0.225 1,=0.047 89,中央5×5部分拟合的均方根误差(RMSE)为0.031 97。拟合结果如图5所示。对图5进行分析可知,像斑源函数能量最大值不在中央,在距中央(–6.0μm,–3.3μm)处。也就是说点源靶标的弥散斑中心与像元中心没有对准,通过拟合并采用拟合结果能量最大值的位置为中心进行能量集中度的计算,可以消除没有对准的影响。得到拟合结果之后,就可以通过两次反卷积求得系统的点扩散函数了。

图5 点源靶标像斑源函数高斯拟合结果
反卷积的结果见图6。每一次反卷积得到的结果在两个方向上都向前平移了矩形窗口长度的一半,进行计算时应平移回原位置。图6(a)是第一次反卷积得到的结果,反映了点源靶标弥散斑分布情况。图6(b)为第二次反卷积的结果,反映了光学系统点扩散函数的分布情况。比较图5和图6(a)、图6(b)可以发现,每一次反卷积都是将函数形状“变瘦”的过程,也就是去除矩形窗口的积分效应的过程。若按照图6(b)计算系统的能量集中度,结果为0.420 1,相比于常规方法计算值有所提高,有效去除了测试时中心偏移以及靶标尺寸对测试结果造成的影响。

(a)第一次反卷积结果
(a)The first deconvoluntion result

(b)第二次反卷积结果
4 结束语
本文提出了一种依据点源靶标像斑推算点目标探测系统能量集中度的方法。相比于传统方法,本文方法能够有效消除测试时像元中心与靶标弥散斑中心未对准的影响,并能够去除靶标尺寸对计算结果的影响,从而获得更精确的能量集中度测试值。在具体操作中,可以通过改变像元与靶标的空间相对位置,获得更多靶标像斑源函数的离散值,提高拟合精度,减小计算误差。本文提出的方法在工程测试中具有参考价值。
(References)
[1] 龙亮, 王世涛, 周峰, 等. 空间红外点目标遥感探测系统在轨辐射定标[J]. 航天返回与遥感, 2012, 33(2): 73-80. LONG Liang, WANG Shitao, ZHOU Feng, et al. In-orbit Radiometric Calibration Methods for Remote Sensing System to Detect Space Infrared Point Target[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(2): 73-80. (in Chinese)
[2] 张伟, 孟祥龙, 丛明煜, 等. 天基红外扫描图像点目标检测算法[J]. 红外与激光工程, 2009, 38(5): 921-925. ZHANG Wei, MENG Xianglong, CONG Mingyu, et a1. Algorithm of Space Point Target Detection for IR Scan Images[J]. Infrared and Laser Engineering, 2009, 38(5): 921-925. (in Chinese)
[3] CASEY E J, KAFESJIAN S L. Infrared Sensor Modeling for Improved System Design[C]. Infrared Imaging Systems: Design, Analysis, Modeling, and Testing VII. Orlando, FL, United States: International Society for Optics and Photonics, 1996.
[4] 张科科, 傅丹鹰, 周峰, 等. 空间目标可见光相机探测能力理论计算方法研究[J]. 航天返回与遥感, 2006, 27(4): 22-26. ZHANG Keke, FU Danyan, ZHOU Feng, et al. The Study on Detect Ability Calculation Method of Space Object Visible Camera[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(4): 22-26. (in Chinese)
[5] COTA S A, KALMAN L S, KELLER R A. Advanced Sensor-simulation Capability[C]. Signal and Image Processing Systems Performance Evaluation. Orlando, FL, United States: International Society for Optics and Photonics, 1990.
[6] 黄继鹏, 王延杰, 孙宏海, 等. 激光光斑位置精确测量系统[J]. 光学精密工程, 2013, 21(4): 841-848. HUANG Jipeng, WANG Yanjie, SUN Honghai, et al. Precise Position Measuring System for Laser Spots[J]. Optics and Precision Engineering, 2013, 21(4): 841-848. (in Chinese)
[7] 曹世康, 李东坚, 许瑞华, 等. 基于最优弧的激光光斑中心检测算法[J]. 红外与激光工程, 2014, 43(10): 3492-3496. CAO Shikang, LI Dongjian, XU Ruihua, et al. Algorithm of Laser Spot Detection Based on Optimal Arc[J]. Infrared and Laser Engineering, 2014, 43(10): 3492-3496. (in Chinese)
[8] 金占雷. CCD光斑质心算法的误差分析[J]. 航天返回与遥感, 2011, 32(1): 38-44. JIN Zhanlei. Error Analysis of Centroid Algorithm Based on CCD[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(1): 38-44. (in Chinese)
[9] 李妥妥, 苏云, 兰丽艳. 低温红外镜头星点检测数据处理方法研究[J]. 航天返回与遥感, 2008, 29(4): 24-29. LI Tuotuo, SU Yun, LAN Liyan. Study on a Method of Data Processing for Star Test of Cryogenic Infrared Lens[J]. Spacecraft Recovery & Remote Sensing, 29(4): 24-29. (in Chinese)
[10] BLACKMAN S, POPOLI R. Design and Analysis of Modern Tracking Systems[M]. Boston, MA: Artech House, 1999: 99-100.
[11] POROPAT G V. Effect of System Point Spread Function, Apparent Size, and Detector Instantaneous Field of View on the Infrared Image Contrast of Small Objects[J]. Optical Engineering, 1993, 32(10): 2598-2607.
[12] 薛峰, 操乐林, 张伟. 点扩散函数对点目标探测性能的影响分析[J]. 红外与激光工程, 2007(2): 177-181. XUE Feng, CAO Yuelin, ZHANG Wei. Research on Effect of PSF on Point Target Detection Performance[J]. Infrared and Laser Engineering, 2007(2): 177-181. (in Chinese)
[13] 杨天远, 周峰, 行麦玲. 空间扫描相机点目标采样系统设计[J]. 航天返回与遥感, 2016, 37(2): 82-92. YANG Tianyuan, ZHOU Feng, XING Mailing. Design of Point Target Sampling System of Space Scanning Camera[J]. Spacecraft Recovery and Remote Sensing, 2016, 37(2): 82-92. (in Chinese)
[14] 李翠萍, 韩九强, 黄启斌, 等. 基于小波变换和高斯拟合的在线谱图综合处理方法[J]. 光谱学与光谱分析, 2011, 31(11): 3050-3054. LI Cuiping, HAN Jiuqiang, HUANG Qibin, et al. An Integrated On-line Processing Method for Spectrometric Data Basedon Wavelet Transform and Gaussian Fitting[J]. Spectroscopy and Spectral Analysis, 2011, 31(11): 3050-3054. (in Chinese)
[15] CHEN Z, CHEN H. New Deconvolution Method for Microscopic Images Based on the Continuous Gaussian Radial Basis Function Interpolation Model[J]. Journal of Biomedical Optics, 2014, 19(7): 687-693.
[16] ARCHER G E, BOS J P, ROGGEMANN M C. Comparison of Bispectrum, Multiframe Blind Deconvolution and Hybrid Bispectrum-multiframe Blind Deconvolution Image Reconstruction Techniques for Anisoplanatic, Long Horizontal-path Imaging[J]. Optical Engineering, 2014, 53(4): 373-373.
[17] 杨怀栋, 徐立, 陈科新, 等. 盲目反卷积光谱图超分辨复原算法[J]. 光谱学与光谱分析, 2007, 27(7): 1249-1253. YANG Huaidong, XU Li, CHEN Kexin, et al. Blind Deconvolution Algorithm for Spectrogram Super-resolution Restoration[J]. Spectroscopy and Spectral Analysis, 2007, 27(7): 1249-1253. (in Chinese)
[18] HUANG H, YANG H, MA S. Gradient-based Image Deconvolution[J]. Journal of Electronic Imaging, 2013, 22(1): 4049-4068.
[19] JANSSON P A, RICHARDSON M. Deconvolution of Images and Spectra[J]. Optical Engineering, 1997, 36(11): 3224-3225.
(编辑:王丽霞)
A Method for Calculating the Energy Concentration Degree of Point Target Detection System
YANG Tianyuan ZHOU Feng XING Mailing
(Beijing Institute of Space Mechanics & Electricity, Beijing 10094, China)
In point target detection system, the energy collected by a single pixel is determined by the energy concentration degree of the optical system, which directly affect the detection signal to noise ratio. It is necessary to test the energy concentration degree after the completion of the camera design to evaluate the performance of the detection system. Traditionally, the energy concentration degree is calculated by dividing the sum of the point image energy by the center pixel energy. But the influence of the center pixel position offset and the size of the point target will lead to a big error. Through the establishment of a point source target imaging model, the influence of the center pixel position offset and the size of the point target is analyzed. The general process is offered for solving the point target energy concentration degree. And an easily achievable calculation method is designed. After the Gaussian fitting of the sampling result, the deconvolution is applied twice to eliminate the influence of the center pixel position offset and the size of the point target, and then the high precision solution of energy concentration degree is obtained. The calculation results show that this method is more close to actual situation than the traditional method, which has engineering application value.
energy concentration degree; Gaussian fit; deconvolution; point target detection; space camera
TP391.41
A
1009-8518(2017)02-0041-07
10.3969/j.issn.1009-8518.2017.02.006
2016-05-11
杨天远,男,1990年生,2016年获中国空间技术研究院飞行器设计专业硕士学位,研究方向为红外系统技术。E-mail: yangtianyuan@163.com。

