盘缝带伞细化结构的仿真影响研究
方世兴 黄伟 荣伟
盘缝带伞细化结构的仿真影响研究
方世兴 黄伟 荣伟
(北京空间机电研究所,北京100094)
在火星探测任务中,盘缝带伞对航天器在低密度大气条件下的减速起到了重要作用。文章采用ProE软件进行几何建模;利用Hyperwork软件进行伞衣有限元建模及前处理;利用LS-DYNA软件的任意拉格朗日–欧拉方法着重研究了径向加强带细化结构对于盘缝带伞无限质量下,流固耦合仿真结果的影响。通过仿真研究发现,在考虑径向加强带细化结构后,缩比的盘缝带伞的阻力系数值与实际试验结果相近,伞衣外形、伞衣摆角与实际试验结果更为接近。此外,考虑径向加强带后,伞衣应力的仿真结果也与真实物理现象更为贴近。文章的建模方法及仿真结果对盘缝带伞的设计与仿真验证具有一定的参考价值。
盘缝带伞 细化结构 流固耦合 有限元方法 回收着陆
0 引言
降落伞在飞船返回着陆、火箭助推器回收、返回式卫星回收以及火星探测器进入着陆等方面,都发挥着重要的作用[1]。深空探测任务已经作为新世纪的探究热点,而火星探测则是目前世界各国深空探测领域的研究重点。火星表面具有稀薄的大气,探测器登陆火星时常采用气动外形与降落伞相结合的减速方案[2]。目前,成功的火星探测任务,大部分采用的降落伞是盘缝带(Disk-Gap-Band,DGB)伞。特殊的火星环境与超声速的开伞条件,使得DGB伞的工作状态更为复杂,难以在地球上直接进行模拟试验[2]。目前国内外主要通过风洞试验、空投试验、高空开伞试验来验证DGB伞的气动性能[3]。但这些试验往往费用较高,又无法涵盖所有的试验工况。因此,基于计算机技术的数值仿真方法就成为关注的热点。
目前有许多适用于降落伞气动性能仿真的数值方法,LS-DYNA软件的任意拉格朗日–欧拉方法(Arbitrary Lagrange Euler,ALE)能有效模拟出低速状态下,降落伞在风洞试验、空投试验中的流固耦合现象,其对应的无限质量[4-5]和有限质量[6]的仿真计算结果也与试验结果相近,验证了ALE方法的有效性。在真实情况下,降落伞的加强带、伞绳及吊带等结构,都是降落伞设计时需要重点关注的对象,也是保证降落伞强度的重要部分[7];而以往国内外的降落伞流固耦合仿真研究中,都对降落伞伞绳、加强带及吊带等结构进行了一定程度的简化[8-10]。在实际的风洞试验中,由于缩比降落伞模型的尺寸较小,这些结构的占比不可忽略,但对试验和仿真结果造成的影响目前尚不明确。国外的Tutt和Lingard团队利用LS-DYNA软件,针对DGB伞模型进行超声速条件下的流固耦合仿真研究,并得到其不同马赫数值条件下的气动特性,但都简化了DGB伞的伞绳及加强带结构[11-13]。文献[14]曾利用浸入式边界法,研究了超声速条件下,柔性及刚性降落伞的气动特性。文献[15]研究了伞绳在超声速条件下刚体化降落伞气动仿真结果的影响,发现伞绳引起的激波与前体及降落伞本身的激波发生耦合。
针对DGB伞的伞绳及加强带结构对DGB伞的流固耦合仿真结果影响,目前国内外的学者还未有过多的研究。因此,本文着重探究DGB伞细化结构对于流固耦合仿真结果的影响。
本文采用ProE软件进行DGB伞缩比模型几何建模,而后利用Hyperwork软件对其进行有限元建模及前处理,并给出了径向加强带细化结构的建模方法;采用LS-DYNA软件的ALE方法,对缩比的普通伞模型(后文称“普通伞”)和含细化结构的细化伞模型(后文称“细化伞”)进行无限质量下的流固耦合仿真研究。文章对比了仿真计算与试验的阻力系数,并在此基础上,对DGB伞径向加强带细化结构带来的影响进行了研究,考察了充气过程伞衣外形、伞衣摆角及伞衣应力的变化情况,结果可为DGB伞的设计与仿真提供参考。
1 DGB伞的流固耦合计算机理
本文所采用的数值仿真软件为LS-DYNA,利用ALE方法[16-18]对DGB伞充气过程进行流固耦合仿真计算。
1.1 结构动力学模型
降落伞伞衣是柔性大变形体,具有典型的非线性动力学特性,而且还是具有透气量的多孔渗透性薄膜结构,则结构边界的动力学模型为[16]:
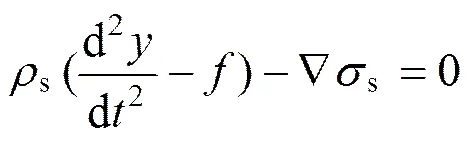
式中为位移矢量;s为材料密度;为作用在结构上的体积力;s为结构的Cauchy应力张量;为积分时间;下标s表示结构。
1.2 流体动力学模型
在ALE方法中,涉及流体的Navier-Stokes控制方程可用质量守恒方程、动量守恒方程和能量守恒方程来表示[16]。
质量守恒方程为:
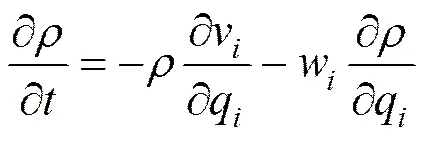
式中代表流体的密度;v代表相对空间域的流体速度;w表示相对参考域的流体速度;q表示流体的欧拉坐标;=,,,表示节点的方向。
动量守恒方程为:
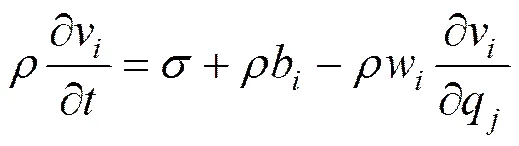
式中为流体的应力张量;b代表流体的体积力;,,表示的,,分量。
的具体形式可表述为:
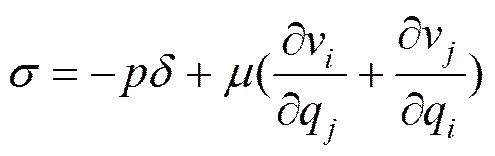
式中为Kronecker函数;为流体的压力;表示流体动力粘性系数。
能量守恒方程为:
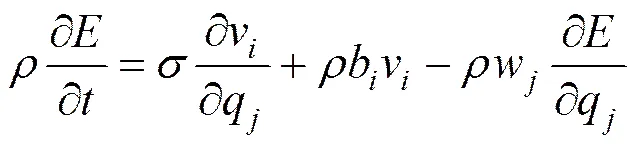
式中表示流体的内能。
1.3 流固耦合算法
本文的数值算法是ALE方法,其主要特点是在建立几何模型和进行有限元网格划分时,固体与流体的几何外形以及对应的网格可以重叠在一起,如图1所示。计算中则通过罚函数约束方法将固体域与流体域耦合在一起,以实现力学参量的传递。
本文的研究对象是DGB伞,其常用的约束方法是罚函数法。罚函数耦合方法是通过数值计算追踪结构的从节点和流体的主物质之间的相对距离,如图2所示。检查每一个从节点对主物质表面的贯穿,如果从节点不出现贯穿,就不进行任何操作;如果发生从节点对主物质表面的贯穿,则界面接触耦合力F就会分布到流体的节点上,界面接触耦合力的大小与发生贯穿的数量呈正比,即:
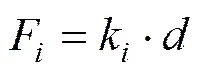
式中k表示基于主从节点质量模型特性的刚度系数,该值与实际的相对距离有关。
图1 流体与固体的网格示意
Fig.1 Mesh of fluid and structure
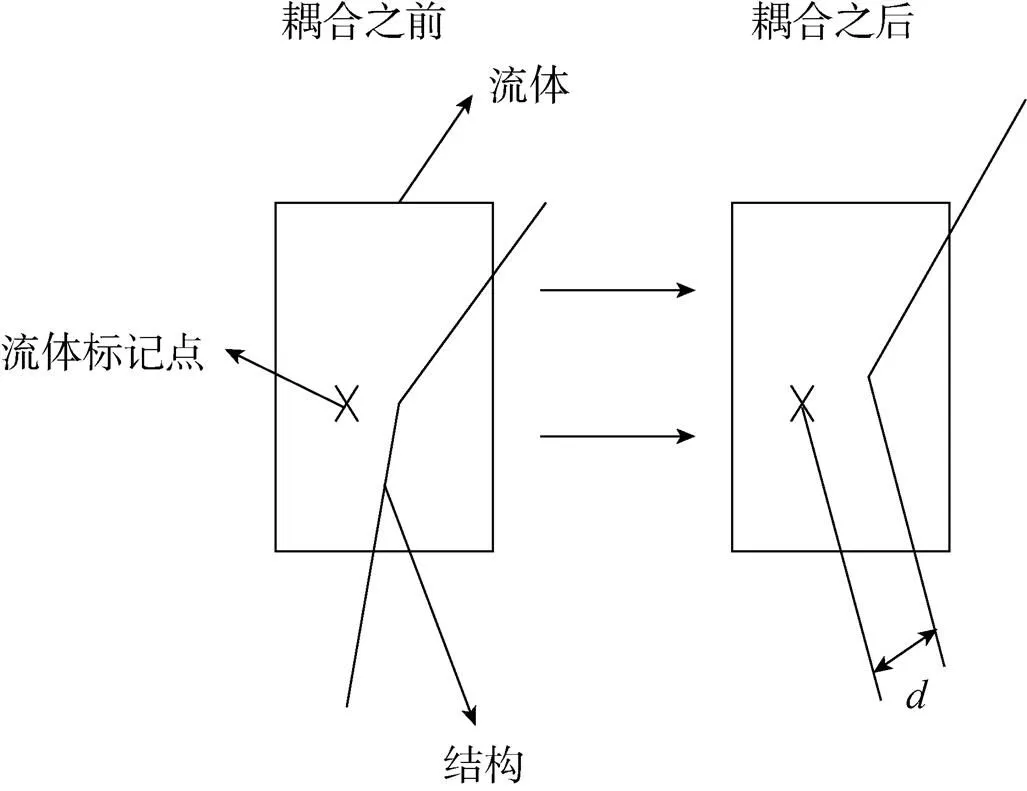
图2 罚函数耦合算法示意
2 仿真模型
本文仿真所采用的DGB伞参考“海盗号”(Viking)降落伞,其伞型参数比例见表1所示[19]。但考虑到计算成本的需要,本文根据某地面风洞试验参数,对DGB伞的模型进行了缩比,见后文所述。
表1 “海盗号”型DGB伞参数比例关系

Tab.1 The parameter relationship of the Viking type DGB parachute
2.1 DGB伞缩比模型参数
DGB伞缩比模型的结构参数如表2所示,其中细化伞在几何建模的时候仅考虑径向加强带,其余细化结构均在有限元建模中予以展示。本文普通伞模型和细化伞模型的伞衣几何建模结果如图3所示。
表2 仿真DGB伞结构参数

Tab.2 The structural parameter of the simulation parachute
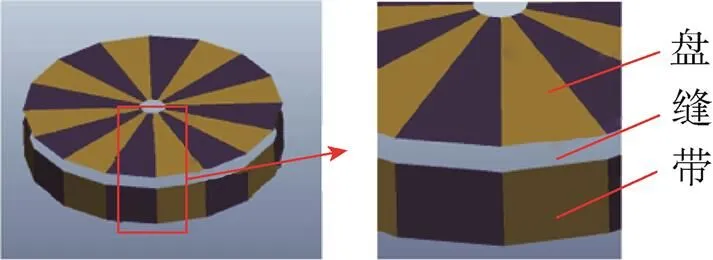
(a)普通伞
(a)Normal parachute

(b)细化伞
通过图3可以得知,细化伞模型与普通伞模型最大的区别,在于细化伞模型具有从伞顶孔到带底部的径向加强带。径向加强带的宽度为3mm,且径向加强带与伞衣完全缝合。
为了提供后续有限元计算的输入条件,本文利用Hyperwork软件对两种DGB伞模型进行网格划分及前处理。单幅伞衣的顶孔边划分为1个单元;盘底边划分为7个单元,伞衣盘部分沿轴向划分为16个单元;伞衣带部分底边划分为7个单元,沿轴向划分为6个单元;为尽快获得稳态数据,仿真模型的伞绳划分为1个单元。
为了探究径向加强带对于DGB伞流固耦合仿真结果的影响,针对LS-DYNA软件流固耦合仿真的要求,本文对普通伞模型的加强带采用1D绳索单元划分,而对细化伞模型的径向加强带则采用2D壳单元划分。经过网格划分后,DGB伞的网格信息如表3所示。
表3 DGB伞网格参数

Tab.3 Mesh parameters of the DGB parachute
2.2 流场模型参数
LS-DYNA软件在进行流固耦合仿真时,其计算总时长与流场网格大小、网格总量有关。为了缩减计算总时长,流场网格设置时仅在伞衣附近区域进行加密,其余区域按线性变化进行设置。为了尽可能模拟出风洞条件,流场域选定为长方体,其中分为流场入口、流场出口、风洞壁面和中心试验段四部分,流场的几何和网格参数见表4所示。为了进一步模拟出无限质量的试验条件,流场入口条件为恒定速度入口条件,流场出口设定为无反射出流条件,风洞壁面设定为无滑移边界条件,中心试验部分设定为满足理想气体状态方程条件。
表4 流场域参数

Tab.4 The parameter of the fluid domain
2.3 仿真工况参数
在火星探测任务中,DGB伞是在超声速条件下进行充气展开的。而在地球环境中,则可以通过风洞试验来测试DGB伞的阻力特性,其测试涵盖低速、亚声速、跨声速和超声速范围[3]。考虑到LS-DYNA软件在低速情况下的仿真结果是具有较高的可信度。因此,为了研究细化结构对于降落伞流固耦合仿真结果的影响,本文选取地球大气条件下的某低速风洞试验参数作为仿真输入条件,并将仿真结果与实际试验值进行对比。仿真对应的风洞试验参数如表5所示,仿真过程中仅考虑伞衣织物透气性,不考虑细化伞径向加强带的透气性。
表5 DGB伞低速风洞试验参数

Tab.5 Low-speed wind tunnel test parameters of DGB parachute
3 仿真结果与分析
3.1 阻力系数的变化分析
仿真所用的DGB伞模型的名义直径为500mm,其名义面积为0.182m2,通过仿真得到的伞衣阻力可以求得阻力系数随着时间的变化,如图4所示。由图4可知,两种DGB伞从仿真初始状态到充满状态的充气时间都相对较短,细化伞在0.2s左右就达到了稳定状态,而普通伞的稳定时间比细化伞更长一些,接近0.35s。细化伞的呼吸频率比普通伞的要大一些,细化伞的阻力系数值比普通伞的要偏大,这与实际的物理建模是符合的。由于径向加强带为2D单元,实际上是增加了伞衣的阻力面积,导致伞衣的阻力增大。经过计算求得,细化伞阻力系数是0.687,与试验结果的误差值为+8.36%,这说明本文细化结构的建模方法和计算结果是可信的。

图4 DGB伞阻力系数与时间的关系曲线
3.2 伞衣外形的变化分析
为了更好地得到细化结构对于DGB伞流固耦合仿真结果的影响,给出了3个任意时刻的伞衣变形图,如图5所示。图中为仿真充气时间。通过对比分析两种不同DGB伞的变形情况,可以发现,在降落伞从初始外形到充气张满的过程中,由于径向加强带刚度较大,细化伞的变形量没有普通伞的大,故外形变化并不剧烈。此外,随着充气时间的推移,细化伞的外形更为饱满,但呼吸频率略比普通伞要大一些。

图5 DGB伞变形示意
图6中显示的是考虑径向加强带细化结构后,DGB伞稳定状态下的变形对比图。通过仿真结果图片可以看出,在未考虑细化结构时,DGB伞的盘与带之间间隙较大,这也说明了加强带对降落伞充气展开的外形会有一定的影响。根据测量的结果显示,考虑细化结构的情况下,细化伞的盘直径为317mm,普通伞的盘直径为315mm;细化伞的实际盘直径较大一些,导致伞衣的阻力面积增大,因此也对仿真结果也造成一定的影响。

(a)普通伞
(a)Normal parachute

(b)细化伞
本文所建立的DGB伞模型尺寸较小,而径向加强带细化结构,除了在尺寸上会对建模结果产生一定的影响,也从材料刚度上对DGB伞产生较大的影响。从理论上来说,当考虑了降落伞加强带后,一定程度上是减小了结构的透气量,而径向加强带刚度较大,变形时会进一步约束细化伞的外形,导致进一步增加了DGB伞的阻力面积。而如上文所述,展开后考虑加强带的降落伞阻力面积更大。但是通过对比实际试验外形结果和仿真结果的外形,如图7所示,细化伞更接近于实际结果;这也说明了在仿真时,需要考虑细化结构带来的影响。
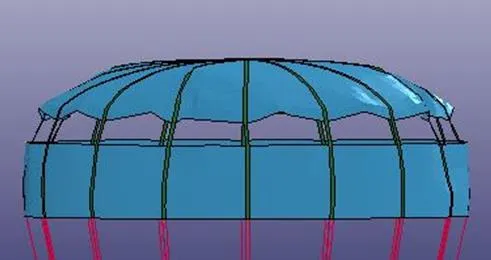
(a)仿真结果
(a)Simulation result

(b)试验结果
3.3 伞衣摆角的变化分析
通过进一步分析仿真计算得到的结果,可以获得DGB伞两种伞模型对应的侧向力系数C(=,),如图8所示。通过图8可以看出,普通伞的侧向力系数明显要比细化伞的大很多,且其值出现类似周期性的变化,这也说明普通伞的摆动较为剧烈。通过图8可以得知,普通伞的向侧向力系数较大,对降落伞的稳定性造成较大的影响。
本文通过分析计算伞顶孔中心位置到伞绳汇交点的向量与DGB伞初始状态轴向向量的夹角,进一步探究细化结构对于仿真结果的影响。伞衣的摆角随着时间变化的曲线如图9所示。风洞试验结果显示,DGB伞在低速情况下的摆角为2°~5°。通过图9可以看出,普通伞的摆角是属于正弦周期的摆动,且摆角在12°~25°之间,摆角较大,与实际的试验值相差较大。而细化伞的摆角则在稳定后基本不变,其摆角在2°~3°之间,与实际的试验值相符。通过对比可以发现,考虑了径向加强带的仿真结果,在降落伞的伞衣摆角上与实际结果更为相近,细化结构在流固耦合仿真时应该予以考虑。
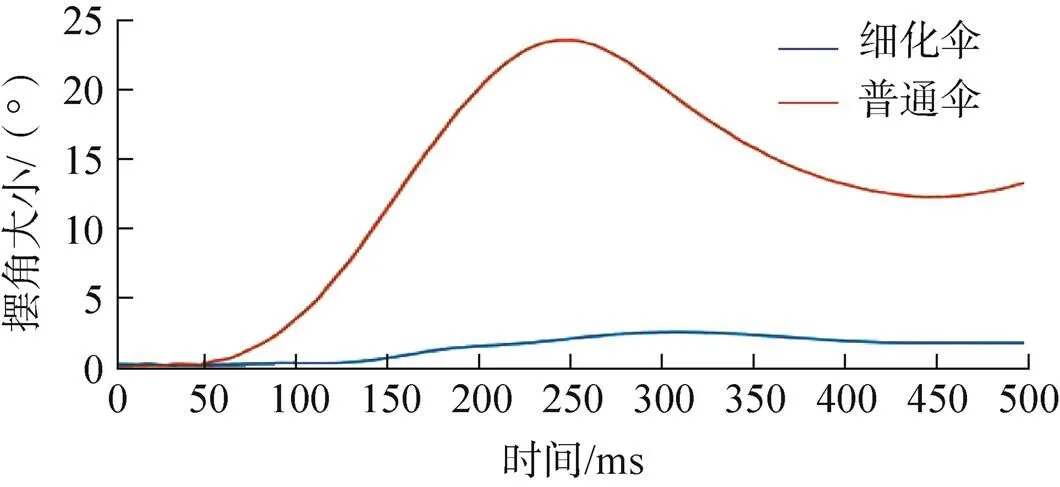
图9 伞衣摆角与时间的关系
3.4 伞衣应力的变化分析
图10是普通伞和细化伞在伞衣应力分布的变化情况。通过对比结果可以发现,细化伞的应力集中分布区域与普通伞的应力集中分布区域有较大的区别。

图10 伞衣应力分布
普通伞的应力集中区域主要是在伞衣盘部分的中间部分和底边部分;而细化伞的应力集中区域则主要在伞顶孔附近的加强带及伞衣径向加强带的邻近部分。通过对比两者可以看出,细化伞的应力集中区域与实际实验中应力集中区域更接近;而实际风洞试验中降落伞在遭受破坏时,也主要是在加强带附近出现撕裂或破坏的情况[7]。此外,细化伞的应力计算值比普通伞更大,能够为降落伞强度设计提供更高的阈值,从而保证降落伞在实际试验中不易遭受破坏。因此,在降落伞的流固耦合仿真中,径向加强带应着重予以考虑,不应忽略。
4 结束语
本文采用软件(ProE和Hyperwork)进行伞衣结构建模,利用ALE方法,着重研究了径向加强带细化结构对于盘缝带伞无限质量下流固耦合仿真结果的影响,并得出以下结论:
1)径向加强带的简化结构和细化结构对降落伞的阻力系数影响不大,细化伞模型的仿真结果在误差允许范围内,说明本文的建模方法与仿真计算方法可信。
2)考虑径向加强带细化结构后,伞衣的变形量较小;细化伞衣外形的仿真结果与实际风洞试验结果更相近,仿真时应考虑细化结构。
3)径向加强带的简化结构对降落伞的摆角产生较大的影响。在考虑细化结构后,盘缝带伞的侧向力系数更小,伞衣摆角更小。因此,在研究降落伞摆动性能时,应考虑径向加强带。
4)考虑细化结构后,盘缝带伞的应力集中主要在径向加强带的细化结构上;对降落伞结构应力的模拟结果更加真实,能够更有效地指导降落伞强度设计工作。
本文仅针对盘缝带伞的风洞试验缩比模型进行了研究,全尺寸条件下细化结构的影响是未来进一步研究的重点。此外,本文研究内容仅考虑了径向加强带细化结构对降落伞仿真结果的影响,未来也可进一步研究伞绳等对仿真结果的影响。在未来的工作中,还可在不同速度条件下,开展更多的降落伞细化结构的流固耦合仿真影响研究,以明确定量的规律。
(References)
[1] 王海涛. 大型降落伞抽打现象及运动稳定性研究[D]. 长沙: 国防科学技术大学, 2011. WANG Haitao. Research on Bull Whipping and Dynamic Stability of Large Parachute System[D]. Changsha: National University of Defense Technology, 2011. (in Chinese)
[2] 荣伟. 火星探测器减速着陆技术研究[D]. 北京: 中国空间技术研究院, 2008. RONG Wei. Mars Exploration Deceleration Landing Technology Research[D]. Beijing: China Academy of Science and Technology, 2008. (in Chinese)
[3] GILLIS G. The Viking Decelerator System an Overview[C]. 4th Aerodynamic Deceleration Systems Conference, Palm Springs, CA, USA, AIAA 1973-442, 1973.
[4] TUTT B, TAYLOR A. The Use of LS-DYNA to Simulate the Inflation of a Parachute Canopy[C]//AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich, Germany, AIAA 2005-1608, 2005.
[5] 高兴龙, 高庆玉, 张青斌, 等. 基于ALE方法的开缝降落伞充气过程研究[J]. 航天返回与遥感, 2013, 34(1): 13-20. GAO Xinglong, GAO Qingyu, ZHANG Qingbin, et al. A Study on the Slots-parachute Inflation Based on ALE Method[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(1): 13-20. (in Chinese)
[6] 程涵, 余莉, 杨雪松, 等. 有限质量情况下降落伞开伞过程数值仿真研究[J]. 空气动力学学报, 2014, 32(2): 259-263. CHEN Han, YU Li, YANG Xuesong, et al. Numerical Simulation of Parachute Opening Process in Finite Mass Situation[J]. Acta Aerodynamica Sinca, 2014, 32(2): 259-263. (in Chinese)
[7] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997. WANG Lirong. Parachute Theory and Application[M]. Beijing: Aerospace Press, 1997. (in Chinese)
[8] 薛晓鹏, 温志涌. 超音速降落伞系统的气动干扰数值模拟研究[J]. 航天返回与遥感, 2016, 37(3): 9-18. XUE Xiaopeng, WEN Chihyung. Numerical Simulation of Aerodynamic Interaction of a Supersonic Parachute System[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(3): 9-18. (in Chinese)
[9] 王中阳. 降落伞充气过程动力学数值模拟[D]. 南京: 南京航空航天大学, 2013. WANG Zhongyang. The Dynamic Numerical Simulation of the Parachute Inflation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese)
[10] 贾贺, 荣伟, 陈国良. 基于LS-DYNA软件的降落伞充气过程仿真研究[J]. 航天器环境工程, 2010, 27(3): 367-373. JIA He, RONG Wei, CHEN Guoliang. The Simulation Research of Parachute Inflation Process Based on LS-DYNA Software[J]. Spacecraft Environment Engineer, 2010, 27(3): 367-373. (in Chinese)
[11] LINGARD J, DARLEY M. Simulation of Parachute Fluid Structure Interaction in Supersonic Flow[R]. AIAA 2005-1607, 2005.
[12] LINGARD J, DARLEY M, UNDERWOOD J. Simulation of Mars Supersonic Parachute Performance and Dynamics[R]. AIAA 2007-2507, 2007.
[13] STEPHEN J L, UNDERWOOD J. Supersonic Tests of the Double Gap Disk-gap Band Parachute and Fluid Structure Interaction Simulation[R]. AIAA 2015-2109, 2015.
[14] XUE Xiaopeng, HIROTO K, YOSHIAKI N. Numerical Simulation on Supersonic Aerodynamic Interference for Rigid and Flexible Parachutes [C]. 42nd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, New Orleans, Louisiana, USA, AIAA 2012-3269, 2012.
[15] XUE Xiaopeng, HIROTO K, YOSHIAKI N, et al. Effects of Suspension Line on Flow Field Around a Supersonic Parachute [J]. Aerospace Science and Technology, 2015, 43: 63-77.
[16] 李裕春, 时党勇, 赵远. ANSYS 11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008. LI Yuchun, SHI Dangyong, ZHAO Yuan. ANSYS 11.0/LS-DYNA Basic Theory and Engineering Application[M]. Beijing: China Waterpower press, 2008. (in Chinese)
[17] 白金泽. LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005. BAI Jinze. LS-DYNA 3D Basic Theory and Application analysis[M]. Beijing: Science Press, 2005. (in Chinese)
[18] 赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003. ZHAO Haiou. LS-DYNA Dynamic Analysis Manual[M]. Beijing : Ordnance Industry Press, 2003.(in Chinese)
[19] 荣伟, 陈旭. 火星探测用降落伞研制试验简介[J]. 航天返回与遥感, 2007, 28(1): 12-17. RONG Wei, CHEN Xu. Introduction of MARS Exploration Parachute Research and Test[J]. Spacecraft Recovery & Romote Sensing, 2007, 28(1): 12-17. (in Chinese)
[20] STELZNERA, CRUZJ, BRUNOR, et al. Opportunities and Limitations in Low-earth Subsonic Testing and Qualification of Extraterrestrial Supersonic Parachute Designs [R].Lanley: NASA Jet Propulsion Laboratory, AIAA2003-2135.
(编辑:陈艳霞)
Study on the Detailed Structure of Disk-Gap-Band Parachute Simulation
FANG Shixing HUANG Wei RONG Wei
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
In the Mars exploration mission, Disk-Gap-Band (DGB) parachute plays an important role in decreasing spacecraft's speed under low density atmosphere conditions. In this paper, ProE software is used to model the geometry of the canopy while Hyperwork software is used for its finite element modeling and pre-processing, and the effect of the radial reinforcement detailed structure of the DGB parachute on the wind tunnel simulation is analyzed by Arbitrary Lagrange Euler (ALE) method of the LS-DYNA software. The simulation results show that when considering the radial reinforcement detailed structure, drag coefficient of the scale canopy is closed to the experiment result, and the shape and swing angle also meet the experiment data. Furthermore, the stress of canopy are also analyzed according to the simulation results after considering the reinforcement detailed structure, which is more closed to actual physical phenomenons. The modeling method and the simulation results in this paper have certain reference value for the design and simulation verification of the DGB parachute.
Disk-Gap-Band parachute; detailed structure; fluid-structure interaction; finite element method; recovery and landing
V445
A
1009-8518(2017)02-0017-10
10.3969/j.issn.1009-8518.2017.02.003
2017-01-10
方世兴,男,1992年生,2014年获北京航空航天大学飞行器设计与工程(航天)专业学士学位,现在中国空间技术研究院飞行器设计专业攻读硕士学位。研究方向为航天器返回与着陆技术。E-mail:fs_xing@163.com。

