高分辨率相机对安装底板微振动幅值的要求分析

刘涌 王巧霞 孙欣 高征



高分辨率相机对安装底板微振动幅值的要求分析

刘涌 王巧霞 孙欣 高征

（北京空间机电研究所，北京 100094）

相机安装底板作为卫星和相机的接口，其微振动量级对卫星、相机都很重要。总体设计经常把相机视为刚体，忽略了相机弹性和扰振频谱的耦合，使得计算出现误差。文章将相机视为弹性体，利用有限元软件和CODEV建立了结构、光学模型，分析了安装底板1μm平动位移以及0.1″转动位移对相机像移的全谱段影响，并反推得到了相机对安装底板微振动的频域要求。结果显示，以像移不超过0.35个像元（像元大小7μm）为指标，某分辨率1m的相机的安装底板在敏感频率处的平动位移幅值不应超过0.01μm，角位移幅值不应超过0.003″，该分析可以为总体设计初期提供参考。

微振动 安装底板 位移要求 空间相机

0 引言

星上活动部件在正常工作时会产生微小的扰振力和扰振力矩，并经由安装底板传递到相机，最终影响成像品质[1-2]。随着遥感技术的发展，分辨率越来越高，相机的焦距也越来越长，相机对卫星上的微振动越来越敏感[3]；另外随着卫星和相机的一体化程度越来越高，微振动振源到相机的传递路径在变短：这两方面的原因使得微振动对相机的影响越来越大。多篇文献均认为微振动对相机成像的影响已经成为不可忽视的因素[4-6]，需要在设计初期就给予重视。而安装底板作为卫星和相机的接口，全频段的微振动量级要求在设计初期对卫星、相机更为重要，例如詹姆斯韦伯天文望远镜（JWST）对望远镜底座的激励要求为不超过0.04μn[7]。

通常反推相机安装底板幅值时将相机角运动等效视为光轴的运动，这种方法首先无法对底板的平动幅值做出衡量，另外也忽视了相机模态频率区间的振动放大效应。本文将相机视为弹性体，计算了底板单位位移传递到相机光学元件的响应以及对成像的影响，根据像移不超过0.35像元反推出相机对底板的微振动振幅要求。

1 刚体相机振幅要求的计算方法

微振动对光学系统的影响主要可以分为以下两部分[8]：

1）光学系统光轴的晃动，各光学元件相互之间无运动，不影响装调关系。主要表现为相机整体微振动造成的像移引起图像拖影及模糊。文献[9]使用视线（line of sight，LOS)变化这一指标进行描述。

2）光路中各镜面之间发生相对运动，偏离各自理想装调位置，主要造成光学系统像差等，使光学系统调制传递函数（MTF）下降。国内对该方面涉及较少，一般将相机视为刚体来评估光轴（或视轴）的运动对像移的影响。

当相机作为刚体时，大量文献均证明平动位移对相机影响很小[10-13]，只考虑平台的角位移，文献[14]给出了相机作为刚体时光轴运动对像移的影响max

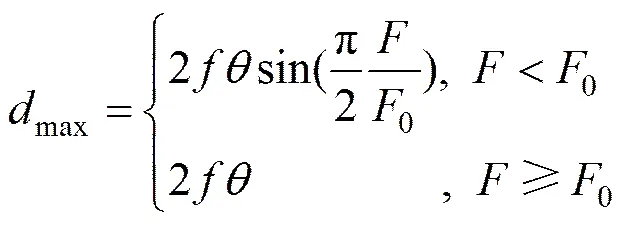
式中为焦距；为不同频率处的相机角位移幅值；为扰振频率；0为转折频率，即以积分时间的2倍对应的振动频率。

一般来说，积分时间内的像移不得超过0.35个像元（根据像移与MTF关系[15-16]，此时造成的相机MTF下降5%）。这里相机参数假设全色相机TDICCD单级0.15ms，级数取最大80级，总的积分时间为0.012s，对应转折频率41.01Hz。根据相关理论，若相机为刚体，安装底部的角位移等于相机角位移，得到刚体相机安装底板在频域内角位移振幅要求可根据式（1）反推，结果见图1。

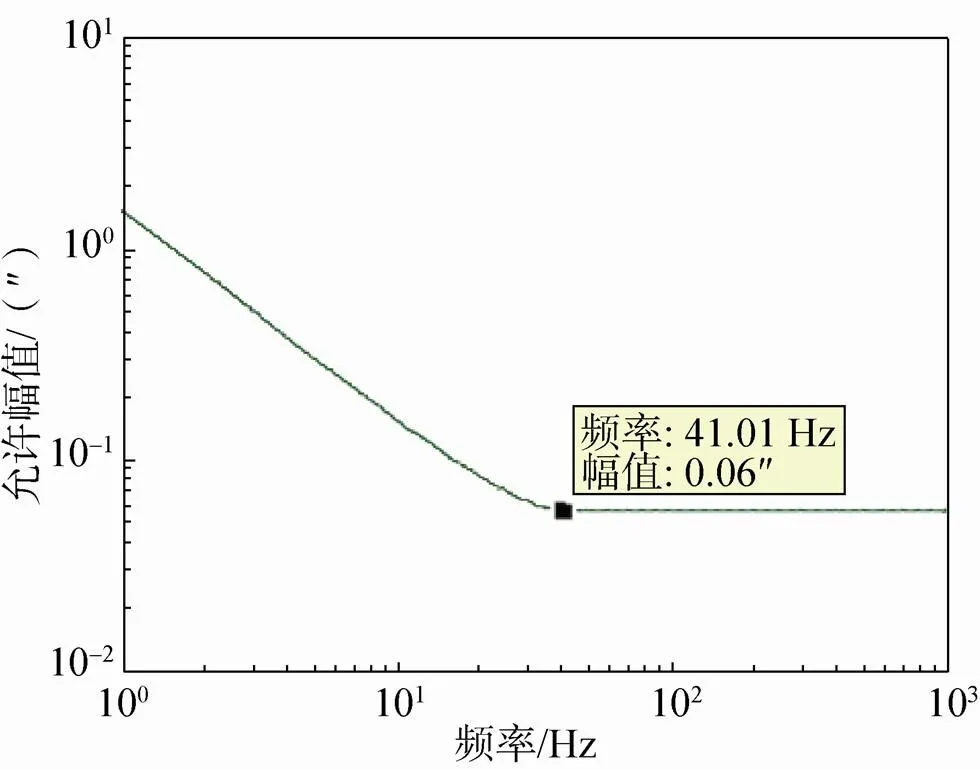
图1 刚体相机对安装底部的角位移频域振幅要求

2 相机作为弹性体的影响

实际上，刚体只是对相机的一种简化，当相机作为弹性体时，相机内部的光学元件和相机安装底部的运动不再保持一致[17]。本文以某分辨率1m的相机（像元大小7μm）为例进行分析。表1为相机单机有限元模态表，有限元分析基频为107Hz。

表1 相机单机有限元模态表

以向（卫星飞行方向）为例（本体坐标系一共三个方向，这里只取向作为计算例子），在安装底板处分别加载1μm振幅的平动位移和0.1″振幅的转动位移，使用模态叠加法对相机进行整机频域分析，频率范围为5~300Hz，模态阻尼0.02得到主镜、次镜的合成角位移幅频响应，见图2。

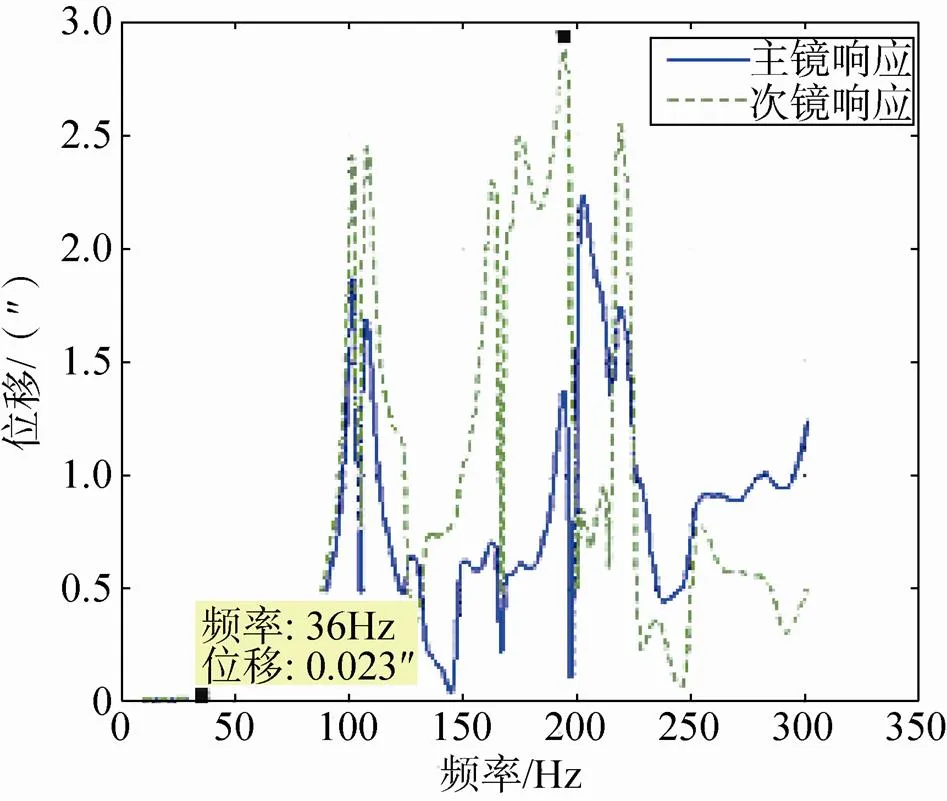
（a）底板向1μm幅值扰振

（a）Flange’s 1 micrometer vibration indirection

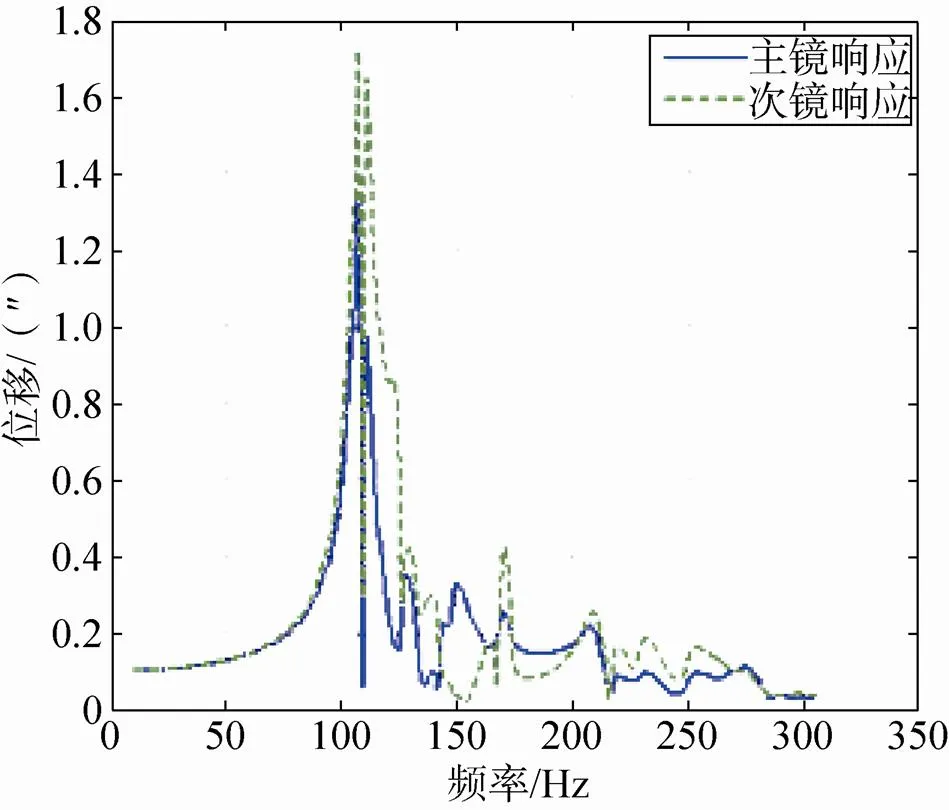
（b）底板产生X向0.1″幅值扰振

由图2可知，安装底板扰振频率在低于相机基频（107Hz）的区域与高于相机的扰振频率表现完全不同。当扰振频率低于相机基频时，相机才可以近似视为刚体，此时底板产生的平动位移造成光学元件的角位移很小，如图2（a）中当扰振频率为36Hz时，底板平动位移造成主次镜的角位移只有0.023″，并且底板产生的角位移基本可以相等地传递到相机，见图2（b）。当扰振频率大于相机扰振基频时，此时相机的弹性带来三个影响：一是底板的平动位移开始起作用，使得光学元件角位移迅速增大，见图2（a）；二是底板的角位移传递到光学元件时会被放大，见图2（b）；三是光路中各镜面之间发生相对运动（角位移不一致），偏离各自理想装调位置。

3 弹性体相机像移的计算方法

相机的弹性在高频区造成光学镜之间的相对运动，这种影响比单纯的光轴晃动要复杂得多：首先光学镜之间的相互运动使得系统不再拥有一个稳定的光轴，式（1）的光轴像移公式不再适用，只能使用CODEV软件进行光线追迹来评估光学系统像移；其次是装调关系的破坏会带来像散、球差、慧差等各种像差。图3给出了使用CODEV仿真的次镜偏离装调与光轴晃动的光路图，可见光学镜偏离装调位置后，光线在焦平面上有明显像差。

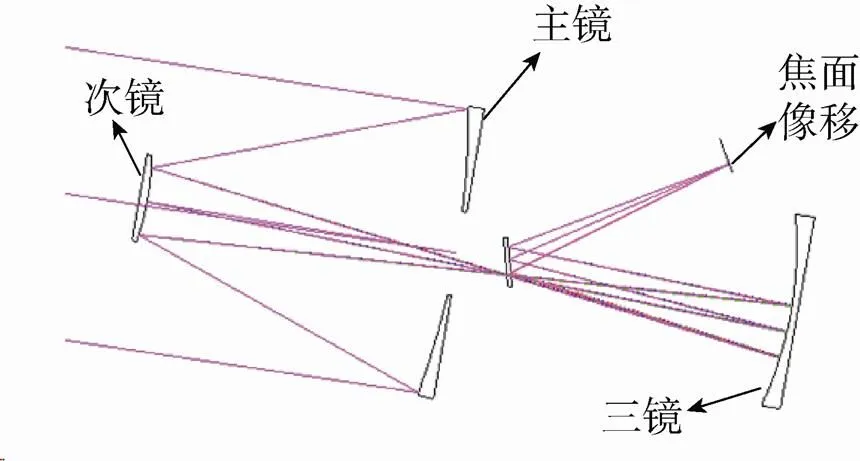
（a）单纯光轴晃动光路图

（a）Optical path of optical axis jitter

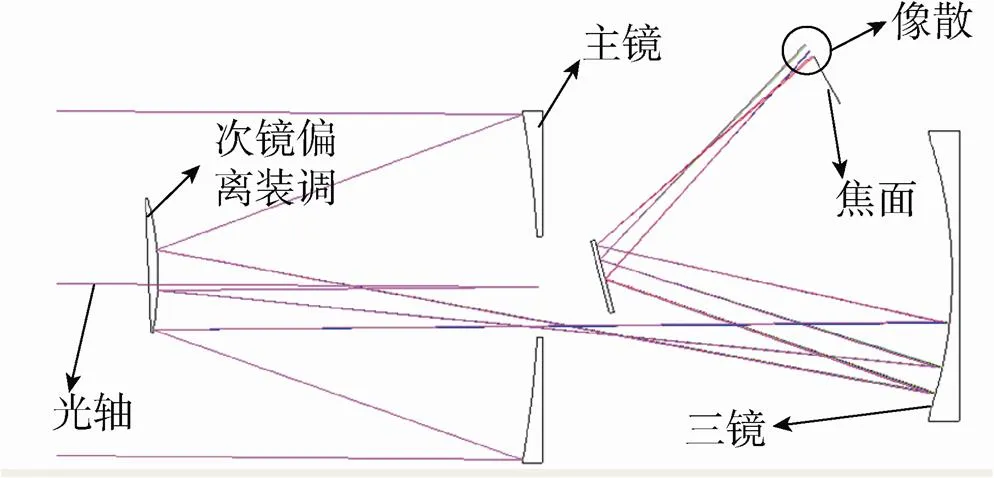
（b）单纯装调改变（次镜偏离）光路图

像移和像差会同时造成MTF的下降，但由于相机是运动中成像，一般像移造成的MTF下降要远大于像差的影响，例如某型号相机在积分时间内次镜偏离装调0.1″，根据CODEV测算，失调像差引起的MTF下降为0.89%，而像移引起的MTF下降可高达4.17%。因此可忽略失调造成的像差，仅考虑其中的像移部分。

根据本文方法可得到的各光学元件六自由度位移响应结果，将其输入到CODEV软件中[18-19]，利用其中的光线追迹或者footprint功能，可以获得主光线的位置变化情况，即为像移。图4给出了频域内安装底板单位扰振时相机的像移情况。

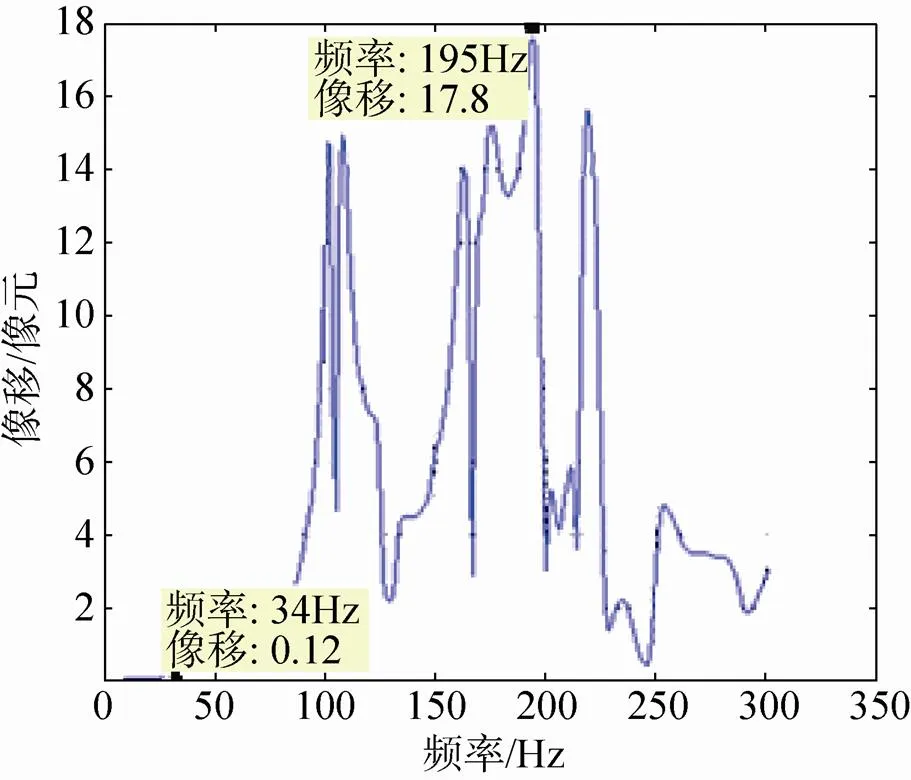
（a）底板向1μm幅值扰振

（a）Flange’s 1 micrometer vibration indirection

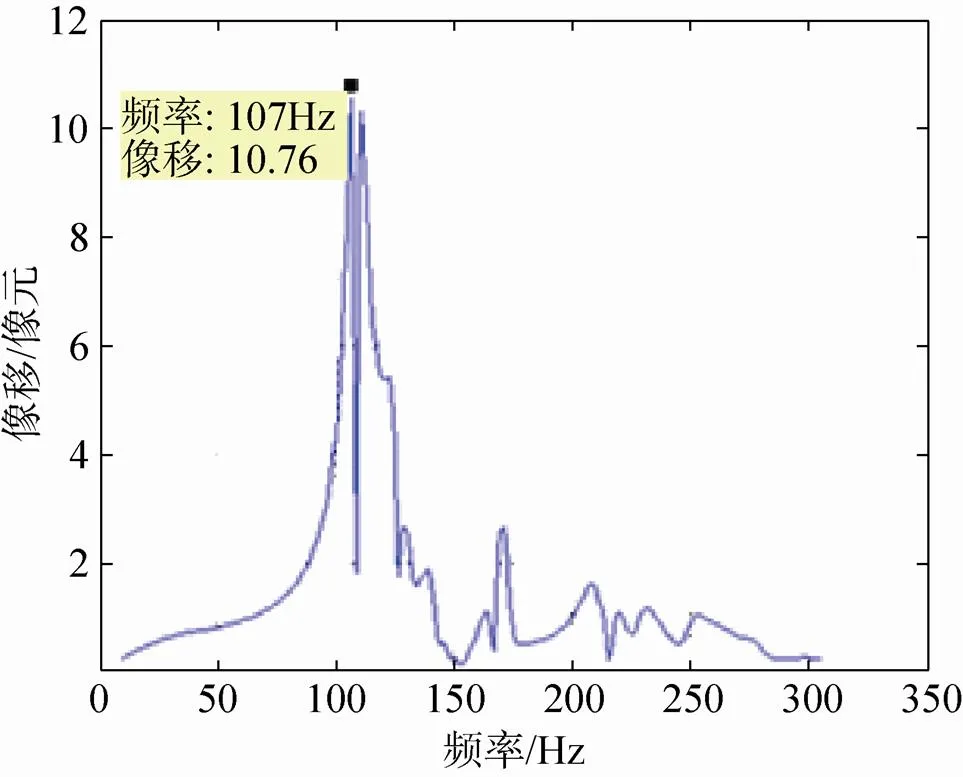
（b）底板产生X向0.1″幅值扰振

图4和图2的形状基本是一致的，相同的扰振下低频段造成的像移较小，当扰振引发相机共振时，像移就会大大提高。例如对于本文中相机，频率34Hz幅值1μm的平动位移，造成的像移为0.12个像元，当频率提高到195Hz时，像移迅速增加到了17.8个像元。

4 弹性体相机的位移要求

以相机像移不超过0.35个像元为指标，假设系统是个线性系统，可以根据图4的频域扰振像移图反求出安装底板允许的扰振幅值，见图5。可见无论对于平动位移还是角位移，高频的要求都要比低频更加严苛。具体到该型号，对于平动位移，要求高于100Hz的扰振幅值不超过0.01μm，角位移在相机固有频率处不超过0.003″，其它高频频率处不超过0.02″。

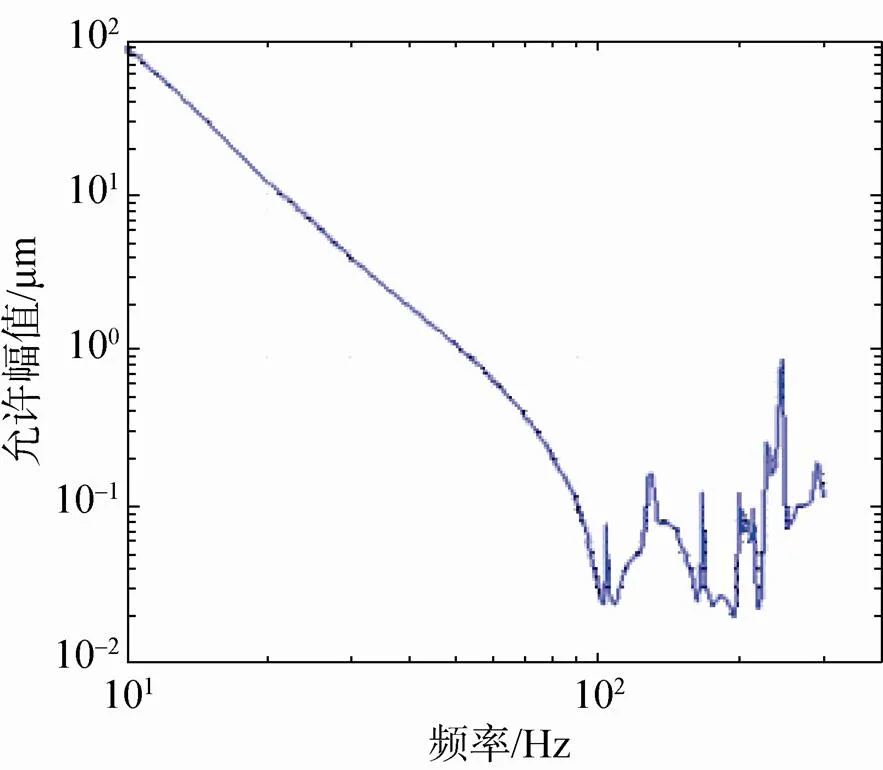
（a）安装底板的平动位移要求

（a）Requirement for translational displacement

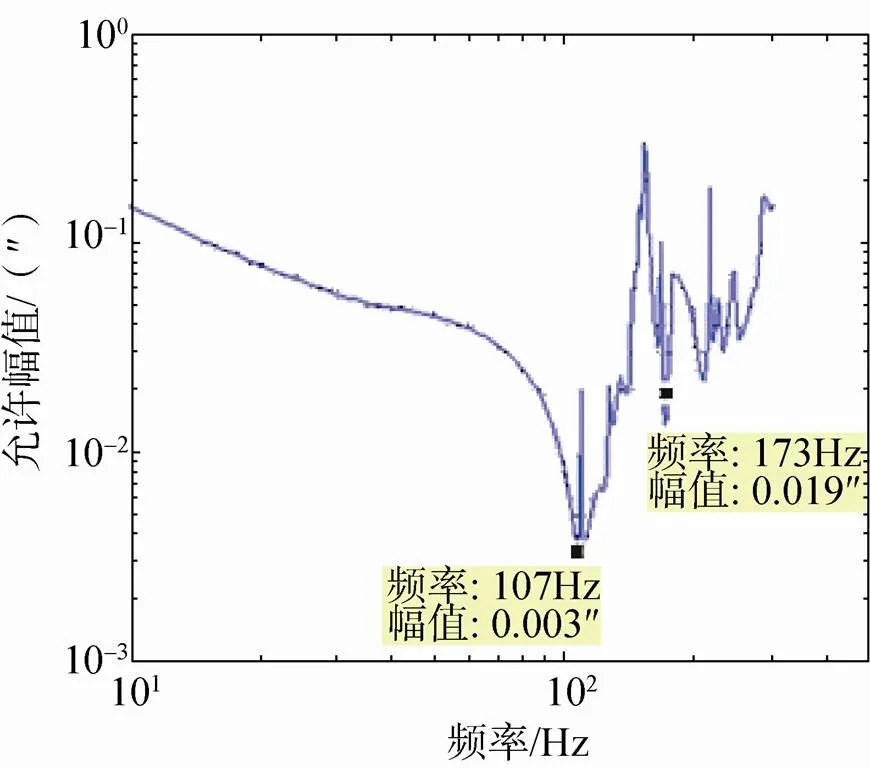
（b）安装底板的转动位移要求

作为对比，图6给出了相机视为刚体和非刚体情况下对安装底板的角位移要求。可以看出，刚体只是弹性体的低频近似；相机视为弹性体，考虑了相机的共振，对安装底板的要求更为严苛。

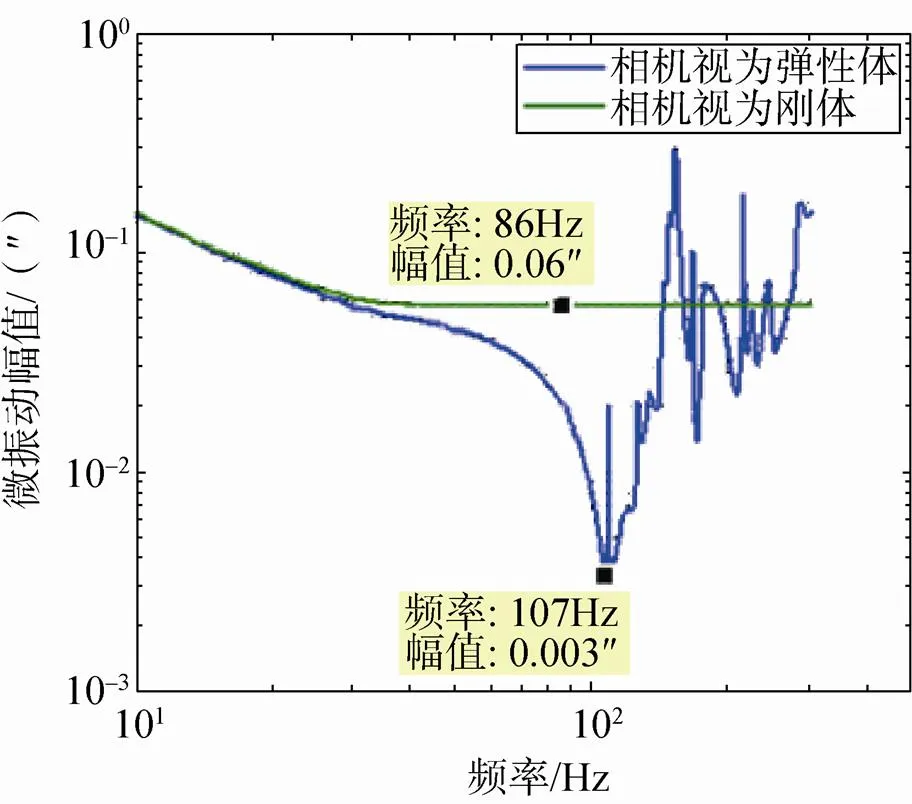
图6 相机视为刚体和视为弹性体的区别

5 结束语

本文将相机视为弹性体，利用有限元软件建立某型号相机结构详细模型，对相机的弹性影响进行了分析，结果表明相机的弹性会使得相机在高频区的响应变大，各光学元件发生装调失调，使得刚体像移公式失效。因此本文根据有限元计算结果使用CODEV软件进行光线追迹，得到了安装底板单位载荷下相机不同频率处的像移，并以像移不超过0.35个像元为指标，反推出安装底板的扰振幅值。结果表明，该相机在敏感频率处的平动位移幅值不得超过0.01μm（折合100Hz处加速度0.4mn），角位移不超过0.003″，其它高频处的角位移则不应超过0.02″。和刚体像移公式相比，本文中的方法不仅可以得到安装底部的角位移幅值要求，也能获得其平动位移幅值要求，而且更真实地反映了相机的高频特征。

(References)

[1] 樊超, 李英才, 易红伟. 颤振对TDICCD相机像质的影响分析[J]. 光子学报, 2007, 36(9): 36-44.FAN Chao, LI Yingcai, YI Hongwei. Influence Analysis of Buffeting on Image Quality of TDICCD Camera[J]. Acta Photonica Sinica, 2007, 36(9): 36-44. (in Chinese)

[2] 庞世伟, 杨雷, 曲广吉. 高精度航天器微振动建模与评估技术最近进展[J]. 强度与环境, 2007, 34(6): 1-9.PANG Shiwei, YANG Lei, QU Guangji. New Development of Micro-vibration Integrated Modeling and Assessment Technology for High Performance Spacecraft[J]. Structure & Environment Engineering, 2007, 34(6): 1-9. (in Chinese)

[3] 孟光, 周徐斌. 卫星微振动及控制技术进展[J]. 航空学报, 2015, 36(8): 2609-2619.MENG Guang, ZHOU Xubin. Progress Review of Satellite Micro-vibration and Control[J]. Acta Aeronautica ET Astronautica Sinica, 2015, 36(8): 2609-2619. (in Chinese)

[4] 徐鹏, 黄长宁, 王涌天. 卫星振动对成像质量影响的仿真分析[J]. 宇航学报, 2004, 24(3): 259-263.XU Peng, HUANG Changning, WANG Yongtian. Modulation Transfer Function in Push-broom Camera Limits Resulting from Mechanical Vibration[J]. Journal of Astronautics, 2004, 24(3): 259-263.(in Chinese)

[5] 李浩洋, 刘兆军, 徐彭梅. 平台颤振对空间光学遥感器成像质量的影响[J]. 计算机仿真, 2012, 29(1): 44-52.LI Haoyang, LIU Zhaojun, XU Pengmei. Influence of Satellite Jitter on Imaging Quality of Space-born Remote Sensing Systems[J]. Computer Simulation, 2012, 29(1): 44-52. (in Chinese)

[6] 邹元杰, 王泽宇, 张志娟, 等. 航天器微振动稳态时域响应分析方法[J]. 航天器工程, 2012, 21(6): 37-42.ZOU Yuanjie, WANG Zeyu, ZHANG Zhijuan, et al. Analysis Method of Steady Time-domain Response for Spacecraft Micro-vibration[J]. Spacecraft Engineering, 2012, 21(6): 37-42.(in Chinese)

[7] BRONOWICK A J. Vibration Isolator for Large Space Telescopes[J]. AIAA Journal of Space and Rockets, 2006, 43(1): 45-53.

[8] 丁延卫, 尤政, 卢锷．航天光学遥感器光机结构尺寸稳定性变化对成像质量的影响[J]. 光学与光电技术, 2004, 2(3): 1-4．DING Yanwei, YOU Zheng, LU E. Influences of Dimension Instability of Space Optical Remote Sensor Opto-structural System on Imaging Quality[J]. Optics & Optoelectronic Technology, 2004, 2(3): 1-4. (in Chinese)

[9] 庞世伟, 史伟哲, 潘腾．遥感卫星微振动问题研究[C]. 高分辨率对地观测学术年会, 北京, 2012:163-170.PANG Shiwei, SHI Weizhe, PAN Teng. The Method to Analysis of Impact by Micro-vibration on Imaging[C]. Proc. of High Resolution Remote Sensing Satellites, Beijing, 2012: 163-170. (in Chinese)

[10] 范大鹏, 刘华, 朱华征．结构振动对卫星图像质量的影响分析[C]//高分辨率遥感卫星结构振动及控制技术研讨会论文集. 长沙, 2011: 52-57.FAN Dapeng, LIU Hua, ZHU Huazheng. Analysis of Impact on Image by Structural Vibraton [C]//Proc. of Structural Vibration and Control of High Resolution Remote Sensing Satellites. Changsha, 2011: 52-57.(in Chinese)

[11] RUDOLER S, HADAR O, FISHER M, et al. Image Resolution Limits Resulting from Mechanical Vibrations, Part 2: Experiment [J]. Optical Engineering, 1991, 30 (5): 577-589.

[12] RUDOLER S, HADAR O, FISHER M, et al. Image Resolution Limits Resulting from Mechanical Vibrations. Part 3: Nnumerical Calculation of Modulation Transfer Function[J]. Optical Engineering, 1992, 31(3): 581-589.

[13] RUDOLER S, HADAR O, FISHER M, et al. Image Resolution Limits Resulting from Mechanical Vibrations. Part 4: Real-time Numerical Calculation of Optical Transfer Functions and Experimental Verification[J]. Optical Engineering, 1994, 33(2): 566-578.

[14] 张博文.微振动对刚体空间相机图像质量的影响分析[C]. 第二届高分辨率对地观测学术年会, 北京, 2013: 47.ZHANG Bowen. Analysis on Effect of Micro-vibration on Rigid-body Space Camera Imaging[C]. Proc. of the Second High Resolution Remote Sensing Satellites, Beijing, 2013: 47. (in Chinese)

[15] 刘良云, 张伯珩, 李英才, 等.航天TDI-CCD相机的MTF和像质分析[J]. 光学技术, 2000, 26(6): 481-483, 485.LIU Liangyun, ZHANG Boheng, LI Yingcai, et al. Analysis of the MTF and Image Quality of TDI-CCD camera[J]. Optical Technique, 2000, 26(6): 481-483, 485.(in Chinese)

[16] 庄绪霞, 王治乐, 阮宁娟, 等. 像移对星载TDICCD相机成像品质的影响分析[J]. 航天返回与遥感, 2013, 34(6): 66-73.ZHUANG Xuxia, WANG Zhile, RUAN Ningjuan, et al. Influence Analysis of Image Motion on Image Quality of Satellite-board TDI Camera Optical System[J]. Spacecraft Recovery & Remote Sensing, 2013, 34 (6): 66-73. (in Chinese)

[17] 刘涌, 胡永力. 动量轮微振动扰振频谱对三反同轴相机的影响[J]. 航天返回与遥感, 2014, 35(5): 31-37.LIU Yong, HU Yongli. Effects of Momentum Wheel Jitter Spectrum on Three-mirror-anastigmatic Imaging[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(5): 31-37.(in Chinese)

[18] 葛东明, 邹元杰. 高分辨率卫星结构-控制-光学一体化建模与微振动响应分析[J]. 航天器环境工程, 2013, 30(6): 586-590.GE Dongming, ZOU Yuanjie. Structure-control-optics Integrated Modeling and Micro-vibration Analysis for High Resolution Satellite[J]. Spacecraft Environment Engineering, 2013, 30(6): 586-590.(in Chinese)

[19] 王红娟, 王炜, 王欣, 等. 航天器微振动对空间相机像质的影响[J]. 光子学报, 2013, 42(10): 1212-1217.WANG Hongjuan, WANG Wei, WANG Xin, et al. Space Camera Image Degradation Induced by Satellite Micro-vibration [J]. Acta Photonica Sinica, 2013, 42(10): 1212-1217.(in Chinese)

（编辑：王丽霞）

Analysis of Mico-vibration Requirement of High Resolution Camera’s Mounting Flange

LIU Yong WANG Qiaoxia SUN Xin GAO Zheng

（Beijing Institute of space Mechanics & Electricity, Beijing 100094, China）

As the interface between satellite and camera, the micro-vibration amplitude of mounting flange is very important. At present, the micro-vibration requirement is put forward with the camera regarded as a rigid body, which ignores the coupling of inherent characteristic mode and micro-vibration spectrum, and then leads to the calculation error. In the article, the camera is regarded as an elastic body and the structural-optical model has been created by the finite element software and CODEV software. The influence on imaging quality of 1μm translation displacement and 0.1″ rotational displacement on mounting flange in whole frequency domain is analyzed, and the frequency requirement of micro-vibration on mounting flange is acquired. The result shows that the pixel displacement indicator is no more than 0.35 pixel(size of 7μm), so for a 1m camera the amplitude of the translational displacement on mounting flange should be no more than 0.01μm and the rotational displacement should be no more than 0.003″ at the sensitivity frequency. The analysis can provides reference for overall preliminary design.

micro-vibration; mounting flange; displacement requirement; space camera

V19

A

1009-8518(2017)02-0027-07

10.3969/j.issn.1009-8518.2017.02.004

2016-01-15

刘涌，男，1989年生，2013年获中国空间技术研究院飞行器专业硕士学位。研究方向为光学遥感器总体设计。E-mail: liuyong19890216@126.com。