翼伞空投系统动力学建模与仿真

周靓 戈嗣诚 张青斌 倪章松



翼伞空投系统动力学建模与仿真

周靓1戈嗣诚2张青斌3倪章松1

（1 中国空气动力研究与发展中心低速空气动力研究所，绵阳 621000）（2 北京空间机电研究所，北京 100094）（3 国防科学技术大学航天科学与工程学院，长沙 410073）

为了解决空中遇险飞行人员的救生问题和实现特殊需求时的精确空投问题，文章针对国内某型号的翼伞空投系统，首先建立了六自由度刚性连接模型，重点分析了翼伞系统的滑翔特性和转弯特性；其次，使用OpenGL动画显示技术对系统轨迹进行了虚拟仿真，使得仿真结果直观化、可视化。仿真结果表明，翼伞受到侧向风作用时会随风漂移，并且漂移速度近似等于风速；翼伞受到单侧下拉偏量作用时会进行转弯运动，且单侧下拉偏量越大，转弯速率越大，转弯半径越小。仿真结果与现有的飞行试验数据一致，证明了模型的正确性和有效性，为翼伞系统在空投上的运用提供了理论支撑。

动力学仿真 可控翼伞系统 动画显示技术

0 引言

翼伞系统在现实运用当中日趋广泛。为了满足不同的应用需求，国内外学者对翼伞-载荷系统进行了不同方法的建模。文献[1]中建立了纵向平面内的三自由度模型，分析了翼伞系统在纵向平面内的静稳定性和动稳定性；在分析和计算气动力和载荷过载的基础上，文献[2]中针对面积为40m2翼伞系统建立了六自由度模型并仿真分析；文献[3]中建立了七自由度模型，并与传统刚体模型进行对比；在六自由度基础上，文献[4]中增加载荷相对于伞体的俯仰和偏航这两个自由度，建立了动力翼伞的非线性八自由度模型；文献[5]和文献[6]中建立了八自由度模型，将仿真数据与实验数据进行对比，验证了模型的正确性；文献[7]和文献[8]则分别建立了九自由度模型并进行仿真和分析；文献[9]建立了十二自由度非刚性连接模型，分析了载荷与伞体之间相对运动的特点，证明了多点交叉连接方式可以抑制两者之间的相对运动。

使用翼伞的精确空投技术，给物资补给问题提供了一个快速并相对廉价的解决方案，尤其是常规补给外的一些急需物资。自上个世纪90年代至今，各国计划实施了多个精确空投系统的项目。其中，颇具代表性的是由美国军方领衔实施的联合精确空投系统（Joint Precision Airdrop System）[10]项目和多个欧盟国组织实施的可折叠、自适应、可操纵的负载纺织机翼结构（Folding，Adaptive，Steerable Textile Wing Structure for Capital Load）[11]项目。由于各国的重视，关于翼伞精确空投的理论研究得到了蓬勃发展。文献[12]针对翼伞系统归航过程中容易受风影响的问题，提出了一种选择性轨迹规划方式来确定翼伞系统所跟踪的预定轨迹；文献[13]提出了一种两点边值贝叶斯曲线轨迹规划方法；文献[14]借助最优控制理论研究了翼伞航迹的分段规划。文献[15]对粒子群优化算法进行改进，并将其应用到翼伞系统的轨迹规划上；文献[16]利用雷达系统测量出风廓信息，然后传送给翼伞控制系统，规划出相应轨迹。

本文针对某翼伞系统的运动特性进行分析，研究其滑翔性能和转弯性能。为了便于工程应用，还对翼伞的运动状态进行可视化显示。在已有软件的基础上，将数字地球模型作为界面的场景，由3ds Max建立翼伞模型，并用OpenGL绘制翼伞运动的轨迹和姿态，进而直观显示翼伞的滑翔特性和转弯特性。最后，为及时定点精确空投，先运用解析法进行初步估算，然后应用了虚拟域变换法，对实时最优末制导的水平路径和偏航角变化进行了数值仿真，分析了这两种方法的现实指导意义和实施的可能性。

1 六自由度翼伞系统动力学模型

1.1 翼伞系统动力学方程的建立

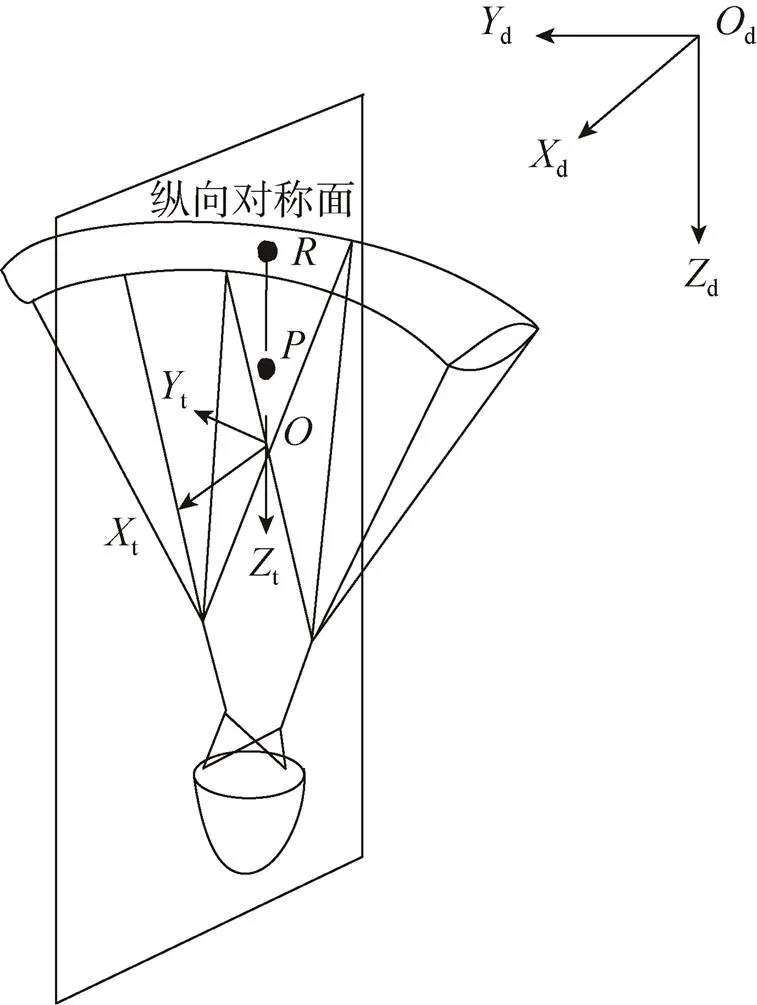
图1 翼伞的纵向对称面示意

假设流体是理想的、无界的和不可压的。借鉴文献[17]对翼伞附加质量的处理方法，即在翼伞系统体坐标系原点位于纵向对称面内这一前提下对某一点的附加质量进行计算的方法，求得附加质量对应的动量和动量矩。

根据动量和动量矩定理，可得：

，，

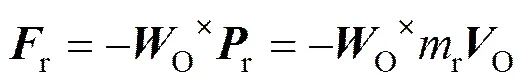
因此，翼伞系统的动力学方程可以表示为：

1.2 翼伞系统飞行特性

翼伞–载荷系统基本参数如表1所示。

表1 翼伞-载荷系统基本参数

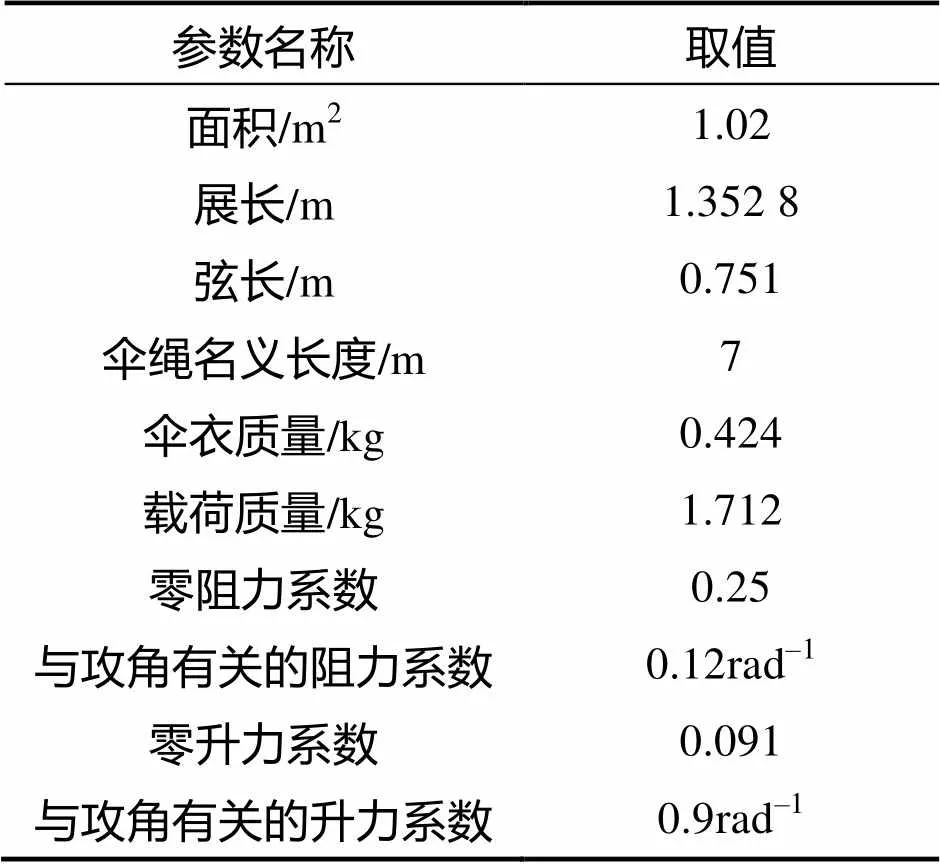
Tab.1 Basic parameters of parafoil-payload system

为了研究单侧下偏量与转弯半径、转弯速率之间的关系，令单侧下偏量分别为，，，，，计算可得相应的转弯半径和转弯速率。表2表示不同的单侧下偏量对转弯半径、转弯速率的影响。

表2 单侧下偏量与转弯速率、转弯半径之间的关系

由图2和图3可知，当翼伞受到侧向风的干扰并且不受到任何操纵时，系统会向风的方向偏转，沿着风的方向速度会先增加后略微减小，最后达到与风速基本相同的速度然后稳定飞行。对翼伞运动进行理论分析可知，转弯运动时翼伞系统会发生倾斜，这使得翼伞系统整体的升力和阻力受到损失，翼伞最终速度有所增加，与图4中所示一致。由图5和图6可知，翼伞系统在达到稳定滑翔状态后在惯性系内做直线运动，飞行轨迹在翼伞系统的纵向对称面内。由图7可知，翼伞系统在单侧下拉后缘量的持续作用下，飞行轨迹会向该侧偏转最后形成转弯运动，运动轨迹在水平面上的投影近似为圆，在惯性系内呈螺旋形。由表2可知，单侧下拉后缘量越大，系统的转弯速率越大，转弯半径就越小，转弯稳定性也会越差。

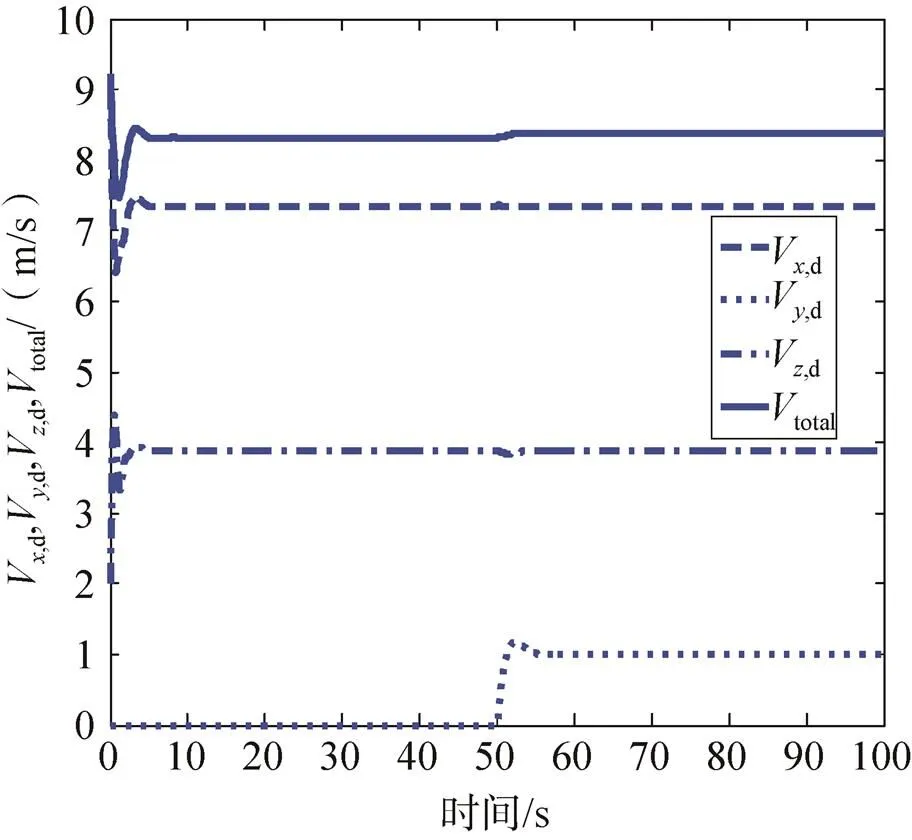
图3 50s后yd轴方向上有匀速风时翼伞滑翔状态速度曲线

图4 50s后加控制时翼伞的速度曲线

图5 无风无控制时翼伞轨迹在Odxdyd平面内的投影

图6 50s后yd轴方向上匀速风时翼伞轨迹在Odxdyd平面内的投影

图7 50s后加控制时翼伞轨迹在Odxdyd平面内的投影

2 仿真平台及可视化

该翼伞仿真软件在以开发平台为Windows操作系统的前提下，充分利用面向对象的程序设计思想，基于OpenGL库，使用Java开发工具、UML2.0建模语言进行开发的仿真程序。其主要任务就是利用加载的轨迹文件和模型文件，通过调用业务逻辑模块绘制出整个降落过程，并在数字地球模型中显示出来。

通过对翼伞滑翔轨迹和转弯轨迹的可视化，我们对翼伞的运动特性有了更直观和更清晰的了解。图8为翼伞模型。图9和图10所示的翼伞三维轨迹图与图2至图7所示的二维轨迹图在运动轨迹的曲线走势上吻合，也符合目前已成功试飞的翼伞在实际条件下无风、受侧向风影响和受单侧下拉后缘量影响时轨迹的基本特征。这充分证明了之前建立翼伞系统六自由度动力学模型正确并且精度较高，在不考虑翼伞与回收物之间的二体运动时具有较强的适应性，在一定的精度范围内可以对翼伞的滑翔距离、横行偏差和飞行稳定性进行估算。

图8 翼伞模型

图9 翼伞的滑翔轨迹和转弯轨迹后视

图10 翼伞的滑翔轨迹和转弯轨迹俯视

3 结束语

本文针对某型号翼伞的飞行特性问题，建立了六自由度动力学模型，分析了翼伞系统的滑翔特性和转弯特性，并将运动轨迹可视化，对比已有的翼伞飞行数据，验证了模型的准确性，为空投实验的实施打下了理论基础，具有一定的参考价值。

(References)

[1] GOODRICK T F. Theoretical Study of the Longitudinal Stability of High Performance Gliding Airdrop Systems[R]. AIAA-75-1394, 1975.

[2] 葛玉君,秦子增.可控翼伞系统的滑翔和稳定性分析[J]. 国防科技大学学报, 1992, 15(4): 16-22. GE Yujun, QIN Zizeng. Gliding and Stability Analysis of Controllable Parafoil System[J]. Journal of National University of Defense Technology, 1992, 15(4): 16-22. (in Chinese)

[3] GORMAN C M, SLEGERS N J. Modeling of Parafoil-payload Relative Yawing Motion on Autonomous Parafoils[C]//Proceedings of the 21th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Eublin, Ireland, 2011: 2011-2614.

[4] 钱克昌, 陈自力. 动力翼伞非线性动力学建模与仿真[J]. 计算机仿真, 2011, 28(12): 9-13. QIAN Kechang, CHEN Zili. Dynamic Parafoil Nonlinear Dynamic Modeling and Simulation[J]. Computer Simulation, 2011, 28(12): 9-13. (in Chinese)

[5] MASAHITO W, YOSHIMASA O. Modeling of Motion Analysis for a Powered Paraglider(PPG)[C]//Proceedings of the 2007 SICE Annual Conference, Japan: Kagawa University, 2007: 3007-3012.

[6] MASAHITO W, YOSHIMASA O. Linear Model of a Powered Paraglider and Observer Design[C]//Proceedings of the 2007 SICE Annual Conference, Japan: The Uiniversity of Electro-communication, 2008: 2135-2140.

[7] 马海亮, 秦自增. 九自由度可控制翼伞系统滑翔及稳定性分析[J]. 国防科技大学学报, 1994, 16(2): 49-53. MA Hailiang, QIN Zizeng. Gliding and Stability Analysis of Nine Degree of Freedom Controllable Parafoil System[J]. Journal of National University of Defense Technology, 1994, 16(2): 49-53. (in Chinese)

[8] 习赵军, 李昌喜. 9自由度精确空投系统的建模与仿真[J]. 华中科技大学学报(自然科学版), 2010, 38(6): 8-11. XI Zhaojun, LI Changxi. Modeling and Simulation of 9 Degree of Freedom Precision Airdrop System[J]. Journal of Huazhong University of Science and Technology (Natural Science), 2010, 38(6): 8-11. (in Chinese)

[9] 熊菁. 翼伞系统动力学与归航方案研究[D]. 国防科学技术大学, 2005.XIONG Jing. Parafoil System Dynamics Research and Homing Scheme[D]. National University of Defence Technology, 2005.

[10] BERLAND J, JUSTIN B, GARGANO B.Precision Delivery of 42 000 Pounds(19 000kg) Under One Parachute[R]. 2009, AIAA 2009-2928.

[11] EDGAR U, CHRISTIAN S, CHRISTIAN U. The FASTWing CL Project-a Self Navigated Gliding System for Capital Loads[R]. 2009, AIAA 2009-2930.

[12] JONATHAN R, NATHAN S. Robust Parafoil Terminal Guidance Using Massively Parallel Proceeding[J]. Journal of Guidance, Control and Dynamics, 2013, 36(5): 1336-1345.

[13] LEE F, JONATHAN R. Bezier Curve Path Planning for Parafoil Terminal Guidance[C]//Proceedings of the 22ndAIAA Aerodyamic Decelerator Systems(ADS) Conference, Deach, FL USA, 2013: 2013-1325.

[14] KAMINER I I, YAKIMENKO O A. On the Development of GNC Algrithm for a High-glide Payload Delivery System[C]// Proceedings of the 42ndIEEE Conference on Decision and Control, Maui, Hawaii USA, 2003: 5438-5443.

[15] LIU Z, KONG J. Path Planning of Parafoil System Based on Particle Swarm Optimization[C]//Proceedings of the 2009 Intenational Conference on Computation Intelligence and Natural Conputing, Beijing, China, 2009: 450-453.

[16] HERMANT T A, WARD M, COSTELLO M, et al. Utilizing Groud-based LIDAR for Autonomous Airdrop[C]//Proceedings of the 22ndAIAA Aerodynamic Decelerator Systems(ADS) Conference, Daytona Beach, FL USA, 2013: 2013-1387.

[17] BARROWS T M.Apparent Mass of Parafoils with Spanwise Camber[J]. Journal of Aircraft, 2002, 39(3): 445-451.

（编辑：刘颖）

Dynamic Modeling and Simulation of Parafoil Airdrop System’s

ZHOU Liang1GE Sicheng2ZHANG Qingbin3NI Zhangsong1

（1 Low Speed Aerodynamic Institude, China Aerodynamics Research and development Center, Mianyang 621000, China）（2 Beijing Institude of Space Mechanics & Electricity, Beijing 100094, China）（3 College of Aerospace and Engineering, National University of Defence Technology, Changsha 410073, China）

In order to solve survival problems of flight crew who meet with danger and realise accurate paradrop when meeting with special situations, this paper is based on some parafoil airdrop system in China, six degrees of freedom rigidity connection model is developed firstly to calculate and simulate the parafoil’s dynamic trajectory, especially analyze gliding and turning features of parafoil system; secondlly, virtual simulation is performed for system by OpenGL animation display technology, making simulation result more visual and direct. The simulation results show that parafoil will drift with the wind and its drift velocity is approximately equal to wind speed and will do turning movement when asymmetric deflection is applied. What’s more, turning speed becomes bigger and turning radius becomes smaller with asymmetric deflection’s increasing. The result is consistent with the existing flight experiment data, so the correctness and effectiveness of the model can be proved. In addition, it can also supply theoretical support for engineering application.

dynamics simulation; controllable parafoil system; animation display technology

V244.21

A

1009-8518(2017)02-0010-07

10.3969/j.issn.1009-8518.2017.02.002

2016-09-29

周靓，女，1992年生，2014年获国防科技大学飞行器系统与工程专业学士学位，2016年获国防科技大学力学专业硕士学位。研究方向为物伞多体系统动力学。E-mail: 1427605572@qq.com。