用地组合形态划分与交通安全影响因素分析

丁 微 徐铖铖 刘 攀

(东南大学交通学院, 南京 210096)

用地组合形态划分与交通安全影响因素分析

丁 微 徐铖铖 刘 攀

(东南大学交通学院, 南京 210096)

为了探究土地利用对交通安全的影响,基于交通事故、交通小区边界、路网、交通流量、人口以及建筑物用地数据,以交通小区为分析单元,将用地特征参数作为聚类指标,利用K均值聚类算法将土地利用划分为5类用地组合形态,采用半参数地理加权回归和方差分析的方法研究用地组合形态对交通安全的影响.结果表明,自然生态型用地形态的事故风险是居住用途主导的用地形态的1.171倍,社区服务型用地形态的事故风险是居住用途主导的用地形态的0.641倍,不同的用地组合形态之间社会经济和交通运行特征差异显著.用地组合形态通过社会经济和交通运行间接地影响交通安全,其中自然生态型的用地形态最安全,社区服务型用地形态最危险,是交通安全管理的重点.

用地组合形态;交通安全;K均值聚类算法;半参数地理加权泊松回归模型;方差分析

Abstract: To investigate the influence of land use on the traffic safety, by taking the traffic districts as the analysis unit and the land-use characteristic parameters as the clustering index, five land-use combinations were divided by using theK-means clustering algorithm based on crash, traffic analysis zone boundary, road network, traffic flow, population and land-use data. The influence of the land-use combinations on traffic safety was studied by the methods of semi-parametric weighted Poisson regression and variance analysis. The results show that the crash risks of ecotype and community service land-use are 1.171 and 0.641 times that of residential land-use, respectively. The social-demographic and traffic parameters of different land-use combinations are significantly different. The land-use combinations indirectly affect the traffic safety through social-demographic and traffic operation. The ecotype land-use combination is the safest, and the land-use combination of community service is the most dangerous which deserves more attention in traffic safety treatment.

Keywords: land-use combinations; traffic safety;K-means clustering algorithm; semi-parametric geographically weighted Poisson regression; analysis of variance

土地利用是交通出行产生和吸引的源头.不同的用地组合形态影响着驾驶员行为、道路条件和交通环境,这些因素与交通事故的发生直接相关.因此,研究不同的用地形态对交通安全的影响,探索用地形态对交通安全的影响机理,是制定合理的用地策略、预防和减少交通事故的有效途径[1].

在研究城市用地与交通安全之间关系时,通常将土地利用特征与交通运行特征、经济社会特征等一起加入宏观交通安全模型中[2-4],对土地利用特征的分析仅以单一的用地参数表征,如用地面积、区域内学校数量等.这种传统的单一用地参数表征方法分立地研究了各类性质的用地对交通安全的影响,没有考虑到区域内不同性质用地间的交互作用,不能充分反映区域的土地利用特征.

本文以交通分析小区为分析单元,将用地规模因素、土地利用密度、用地类别和用地混合度等方面的用地特征参数作为聚类指标,将交通分析小区内土地利用划分为若干用地形态,通过用地组合形态表征土地利用特征,定量评估土地利用对交通安全的影响,并探索不同用地形态下影响交通安全的用地特征、社会经济特征与交通运行特征参数,为考虑道路交通安全的土地利用规划提供参考.

1 数据

1.1 数据来源

本文采用加利福尼亚州Los Angeles县(共计2 244个交通分析小区)2010年的数据.这些数据为GIS格式,包括交通事故、交通分析小区边界、路网、交通流量、人口以及建筑物用地性质数据.

交通事故数据来源于加州大学伯克利分校交通安全研究与教育中心.2010年Los Angles县共有50 683起交通事故,2 244个交通分析小区中事故频数最少的为0,最多的为321起.

人口数据、交通分析小区边界数据以及路网数据均来源于美国人口调查局.路网数据分为高速公路和地方道路2类.交通流量数据来源于公共工程部门,包括年平均日车辆里程和货车年平均日交通流量.

建筑物用地性质数据来源于Los Angles县区域规划部门,共计6 735条建筑物用地记录.建筑物用地基本性质分为10类:住宅类、交通类、公用设施类、工业类、办公类、零售类、物流仓储类、社区服务类、休闲娱乐类和自然保护区.

1.2 数据处理

交通分析小区是交通研究的基本划分单元,连接了交通运行特征与土地利用特征以及人口经济特征.本文采用交通分析小区作为基本的分析单元.使用ArcGIS 10.1软件的标识工具将上述数据匹配到对应的交通分析小区,然后基于交通分析小区编号进行整合,得到的数据集共计2 244条记录.在后续分析中需要以下数据:

1) 交通分析小区交通事故频数.

2) 交通分析小区内各类建筑物用地比例,其计算公式为

(1)

式中,Pi,r为第i个交通分析小区中第r类建筑物的用地比例;Si,r为第i个交通分析小区中第r类建筑物的用地面积;Oi为第i个交通分析小区的用地面积.

3) 交通分析小区用地混合度,其计算公式为[5]

(2)

式中,Mi为第i个交通分析小区的用地混合度;R为建筑物用地类别数.

4) 用地密度,即交通分析小区建筑物用地总面积除以交通分析小区的面积.

5) 用地规模,即交通分析小区内建筑物用地面积之和.

6) 人口密度,即交通分析小区人口数除以交通分析小区的面积.

7) 年平均日车辆里程.

8) 货车年平均日交通量.

9) 高速公路长度.

10) 高速公路比例,其计算公式为

(3)

式中,Ei为第i个交通分析小区高速公路所占比例;Li为第i个交通分析小区地方道路长度,km;Fi为第i个交通分析小区高速公路长度,km.

2 数学模型

2.1 K均值聚类算法

K均值聚类算法具有复杂度低、收敛速度快等特点,相比于其他复杂的聚类算法更适合于处理本文这种大数据集.对于不同的聚类变量和分类数组合形成的多个聚类方案,本文采用戴维森堡丁指数的方法[6]进行方案选择.根据此方法,使得下式值最小的组合即为最优的聚类方案:

(4)

式中,K为聚类数;Qc和Qt分别为第c个分类和第t个分类的类内质心距离均值;dc,t为第c个分类和第t个分类的类间质心距离.戴维森堡丁指数值越小表示类内差异越小,类间差异越大,则该聚类方案越优.

2.2 半参数地理加权泊松回归模型

半参数地理加权泊松回归模型适用于具有空间相关性和异质性的数据集,一般形式为

(5)

式中,λi为第i个交通分析小区事故频数的期望值;(ui,vi)为第i个交通分析小区质心的二维坐标;βj(ui,vi)为第i个交通分析小区中第j个局部解释变量xij的回归参数,该参数随交通分析小区变化而发生变化;γl为第l个全局解释变量zil的回归参数,该参数与交通分析小区i无关;εi为误差项.

地理加权回归模型中依据局部光滑的原则,利用加权最小二乘法来估计模型参数βj(ui,vi),表示为

(7)

式中,wia为第i个交通分析小区进行参数估计时赋予第a个交通分析小区的权重;Gia为第i个和第a个交通分析小区的质心距离;bi为第i个交通分析小区进行参数估计时的带宽.

3 结果与讨论

3.1 聚类结果

本文采用K均值聚类算法对交通分析小区的用地组合形态进行分类,以戴维森堡丁指数作为聚类结果的评价标准.当K=5,将用地混合度和各类建筑用地比例作为聚类变量时,戴维森堡丁指数达到最小值.用地组合形态被分为如下5类:自然生态型用地组合形态、居住用途主导的用地组合形态、商业用途主导的用地组合形态、休闲娱乐用途主导的用地组合形态和社区服务型用地组合形态.表1给出了不同用地组合形态的聚类中心.由表可知:

表1 不同用地组合形态的聚类中心

1) 商业用途主导的用地组合形态下交通分析小区的零售类建筑用地比例较大,达到1.44%,辅以少量办公和休闲娱乐建筑.样本中有466个交通分析小区被分到此类用地组合形态,平均交通事故为35起.

2) 自然生态型用地组合形态的用地混合度在5类中最小,达到0.115,自然保护区用地的比例最大,达到81.02%.样本中8.16%的交通分析小区被分到该用地组合形态,平均交通事故25起.图1描述了5类用地组合形态的交通分析小区交通事故频数特点,总体交通事故频数n的15%分位数为11起,中位数为29起,85%分位数为59起.用地组合形态2中,少于11起交通事故的交通分析小区累积比例在5类用地组合形态中最大,多于59起交通事故的交通分析小区累积比例在5类用地组合形态中最小.

图1 不同用地组合形态下的交通分析小区事故频数特点

3) 休闲娱乐用途主导的用地组合形态下,休闲娱乐类建筑物用地比例较大,达到60.96%,辅以少量零售类建筑.样本中22.28%的交通分析小区被分到了此用地组合形态,平均交通事故为36起.

4) 社区服务型用地组合形态的用地混合度达到0.266,在5类用地组合形态中最大.社区服务类建筑用地比例较大,达到9.74%,辅以少量的住宅类建筑用地.样本中964个交通分析小区被分到此用地组合形态,平均交通事故为37起.图1中,对于这类用地组合形态,少于11起交通事故的交通分析小区累积比例在5类用地组合形态中最小,多于59起交通事故的交通分析小区累积比例在5类用地组合形态中最大.

5) 居住用途主导的用地组合形态下住宅建筑用地比例较大,达到64.35%,辅以少量的社区类建筑.样本中5.84%的交通分析小区被分到该用地组合形态,平均事故为32起.

3.2 用地组合形态对交通安全的影响

针对事故数据的莫兰检验结果表明,莫兰指数值为4.84×10-3,显著性水平p<0.001,说明事故数据呈现出显著的空间集聚特征[7],因此本文采用半参数地理加权泊松回归模型.以居住用途主导的用地组合形态作为参照,其他4类用地形态采用4个哑然变量表示,k1～k4表示其对应系数,利用GWR 4.0软件进行模型参数估计,结果见表2.

表2 半参数地理加权泊松回归模型参数估计结果

模型中年平均日车辆里程的参数都为正值,表明年平均日车辆里程与交通事故频次呈正相关,这与文献[8-12]的结果一致.参数变化范围为[0.344,2.113],具有较为明显的空间不稳定性,说明该模型较好地捕捉到事故和年平均日车辆里程的空间异质性关系,模型具有合理性.

以居住用途主导的用地组合形态作为参照,社区服务型用地组合形态的参数中位数为0.158,在5类用地组合形态中最大.社区服务型用地组合形态、商业用途主导的用地组合形态、自然生态型用地组合形态和休闲娱乐用途主导的用地组合形态的事故风险分别为居住用途主导的用地组合形态的1.171,1.079,0.641和1.125倍.因此,5类用地组合形态中,自然生态型用地组合形态对应安全水平最高,社区服务型用地组合形态对应安全水平最低,是交通安全管理的重点.

3.3 用地组合形态对交通安全的影响机理

为了进一步考察不同用地组合形态下安全风险等级不同的原因,选取了年平均日车辆里程、货车年平均日交通量、高速公路长度比例、人口密度4个关键参数进行研究.对这些参数进行单因素方差分析,结果见表3.由表可知,在95%的置信水平下,不同用地组合形态之间社会经济与交通运行特征参数差异显著.

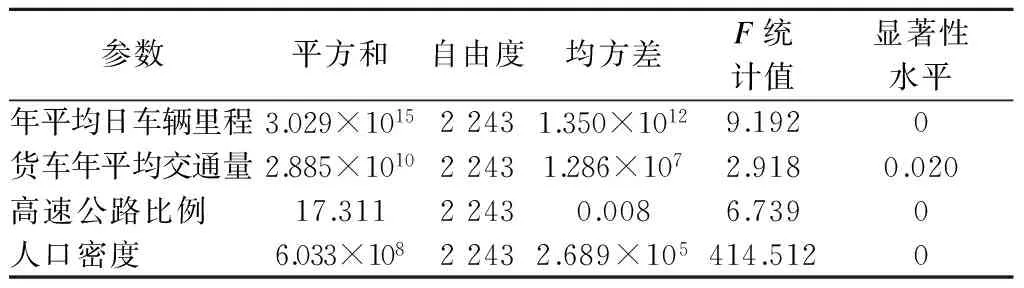
表3 单因素方差分析结果

单因素方差分析只能研究不同用地形态之间是否存在显著差异,无法获知具体的差异情况.本文采用累积分布曲线图来研究差异趋势.图2为不同用地组合形态下上述参数的累积分布曲线.由图可知,安全水平较低的用地组合形态对应着较大的年平均日车辆里程、货车年平均日交通量和人口密度,而安全水平较高的用地组合形态对应着较大的高速公路长度比例,这与文献[8-12]的结果一致.综合单因素方差分析结果和累积分布曲线图可以发现,用地组合形态通过影响社会经济特征与交通运行间接地影响着交通安全.

(a) 年平均日车辆里程

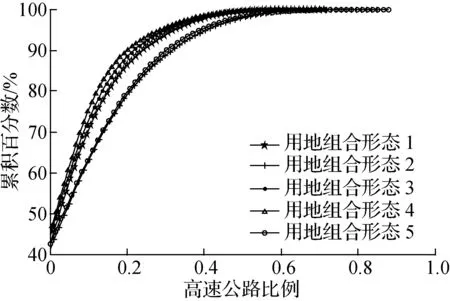
(c) 高速公路比例

4 结论

1) 根据用地混合度和用地比例指标可将用地组合形态分为5类:自然生态型用地组合形态、居住用途主导的用地组合形态、商业用途主导的用地组合形态、休闲娱乐用途主导的用地组合形态和社区服务型用地组合形态.

2) 用地组合形态对交通安全影响显著,自然生态型用地组合形态对应安全水平最高,社区服务型用地组合形态对应安全水平最低,是交通安全管理的重点.

3) 不同用地组合形态之间的社会经济与交通运行特征参数存在的显著差异,是用地组合形态影响交通安全水平的原因.

References)

[1] 唐珏琳.城市规划中的交通安全因素分析[J].公路与汽运,2007(4):47-48,103. DOI:10.3969/j.issn.1671-2668.2007.04.019.

[2] Pulugurtha S S, Duddu V R, Kotagiri Y. Traffic analysis zone level crash estimation models based on land use characteristics[J].AccidentAnalysisandPrevention, 2013,50(1): 678-687. DOI:10.1016/j.aap.2012.06.016.

[3] Amohgyimah R, Sarvi M, Saberi M. Investigating the effects of traffic, socioeconomic, and land use characteristics on pedestrian and bicycle crashes: A case study of Melbourne, Australia[J].JournalofBiomechanics, 2016,48(7): 1325-1330.

[4] Wang X, Yang J, Lee C, et al. Macro-level safety analysis of pedestrian crashes in Shanghai, China[J].AccidentAnalysisandPrevention, 2016,96: 12-21. DOI:10.1016/j.aap.2016.07.028.

[5] Yasmin S, Eluru N. Latent segmentation based count models: Analysis of bicycle safety in Montreal and Toronto[J].AccidentAnalysisandPrevention, 2016,95(Pt A): 157-171. DOI:10.1016/j.aap.2016.07.015.

[6] Yannis G, Papadimitriou E, Antoniou C. Multilevel modelling for the regional effect of enforcement on road accidents[J].AccidentAnalysisandPrevention, 2007,39(4): 818-825. DOI:10.1016/j.aap.2006.12.004.

[7] Li Z, Wang W, Liu P, et al. Using geographically weighted poisson regression for county-level crash modeling in California[J].SafetyScience, 2013,58(10): 89-97. DOI:10.1016/j.ssci.2013.04.005.

[8] 李杨.基于数据分析的交通事故预测方法[J].电子技术与软件工程,2016(21):171. Li Yang. Traffic accident prediction method based on data analysis[J].ElectronicTechnology&SoftwareEngineering, 2016(21): 171. (in Chinese)

[9] Huang H, Abdelaty M A, Darwiche A L. County-level crash risk analysis in Florida[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2010,2148: 27-37. DOI:10.3141/2148-04.

[10] 张铁军,唐琤琤,康云霞,等.Poisson系列交通事故预测模型特点分析及应用[J].公路交通科技,2010,27(6):132-137. DOI:10.3969/j.issn.1002-0268.2010.06.024. Zhang Tiejun, Tang Chengcheng, Kang Yunxia, et al. Analysis of Poisson traffic accident prediction models and their application[J].JournalofHighwayandTransportationResearchandDevelopment, 2010,27(6): 132-137. DOI:10.3969/j.issn.1002-0268.2010.06.024.(in Chinese)

[11] 季彦婕,王炜,邓卫.道路交通事故多因素时间序列宏观预测模型[J].武汉理工大学学报(交通科学与工程版),2006,30(3):433-436. DOI:10.3963/j.issn.2095-3844.2006.03.018. Ji Yanjie, Wang Wei, Deng Wei. Multi-factor time series model for macro-level road accident prediction[J].JournalofWuhanUniversityofTechnology(TransportationScienceandEngineering), 2006,30(3): 433-436. DOI:10.3963/j.issn.2095-3844.2006.03.018.(in Chinese)

[12] 黄合来,邓雪,许鹏鹏.考虑空间自相关的贝叶斯事故预测模型[J].同济大学学报(自然科学版),2013,41(9):1378-1383. DOI:10.3969/j.issn.0253-374x.2013.09.016. Huang Helai, Deng Xue, Xu Pengpeng. Bayesian crash prediction model based on a consideration of spatial autocorrelation[J].JournalofTongjiUniversity(NaturalScience), 2013,41(9): 1378-1383. DOI:10.3969/j.issn.0253-374x.2013.09.016.(in Chinese)

Classificationofland-usecombinationsandanalysisofinfluencingfactorsontrafficsafety

Ding Wei Xu Chengcheng Liu Pan

(School of Transportation, Southeast University, Nanjing 210096, China)

U491.31

A

1001-0505(2017)05-1074-05

2017-01-16.

丁微(1992—),女,硕士生;刘攀(联系人),男,博士,教授,博士生导师,liupan@seu.edu.cn.

国家自然科学基金资助项目(51508093).

丁微,徐铖铖,刘攀.用地组合形态划分与交通安全影响因素分析[J].东南大学学报(自然科学版),2017,47(5):1074-1078.

10.3969/j.issn.1001-0505.2017.05.037.

10.3969/j.issn.1001-0505.2017.05.037