沥青混合料高温蠕变失稳点预测模型及参数影响

顾兴宇 吕俊秀 张小元 邹晓勇

(1东南大学交通学院, 南京 210096)(2金华市公路管理局, 金华 321103)

沥青混合料高温蠕变失稳点预测模型及参数影响

顾兴宇1吕俊秀1张小元1邹晓勇2

(1东南大学交通学院, 南京 210096)(2金华市公路管理局, 金华 321103)

基于压剪破坏理论,建立了密级配沥青混合料高温蠕变失稳点预测模型,并研究了模型参数的影响因素．利用三轴压缩试验,获得沥青混合料不同围压下高温抗压强度和抗剪强度参数．在相同温度及对应围压下,实施不同载荷水平的三轴动态蠕变试验,得到混合料高温失稳点对应的流变次数FN,分析了不同围压下FN变化规律,建立了一个新的预测FN模型．此外,通过试验对掺加不同添加剂混合料的FN预测值进行了验证,进一步分析了级配及温度对模型参数的影响．结果表明,沥青混合料失稳点FN预测结果与试验结果有较好一致性,改变级配或试验温度均会对预测模型参数产生较大影响,而添加剂的影响则可忽略,当温度为60 ℃时AC20级配混合料参数a，b值比AC13级配参数分别减小约52.1%，18.3%,且同一级配材料随温度升高,参数a波动较大,b则增长明显．

沥青混合料;蠕变失稳点;三轴试验;预测模型

Abstract: The prediction models of the creep instability points of dense-graded asphalt mixtures were established at high temperatures, and the influence factors of model parameters were studied, based on the pressure-shear failure theory. First, the compressive strength values under different confining pressures and shear strength parameters were obtained through triaxial compression tests at high temperatures. Secondly, multiple repeated pressure values were applied to dynamic triaxial creep tests at the same temperature and corresponding confining pressure, and the rheological numbers (FN) corresponding to the creep instability points of the asphalt mixtures were obtained. Thirdly, the prediction models of the asphalt mixtures were established by analyzing the change law ofFNunder different confining pressures and cyclic loading pressures. Finally, theFNvalues of the different additive mixtures were predicted using the models. The reliability of the prediction results was verified by the test. Furthermore, the influence factors of model parameters were studied by changing the graduation and test temperatures. Results show that the predictedFNvalues of the asphalt mixtures are in agreement with the experimental results, and the model parameters are affected by the graduation and test temperatures. But the influence of additive can be ignored. The parametersaandbof AC20 gradation mixture are reduced by nearly 52.1% and 18.3%, respectively. The parameterawaves significantly, and the parameterbincreases obviously with the increase of the temperature under the same gradation mixture.

Keywords: asphalt mixture; creep instability points; triaxial test; prediction model

车辙是我国半刚性基层沥青混凝土路面的主要破坏形式之一,其中失稳型车辙的出现严重地降低了路面的平整度及安全性[1-2]．国内外在进行高温车辙变形研究过程中,常采用单轴及三轴静态或动态蠕变试验[3-4]．文献[5-6]模拟了实际路面受力,提出了基于实际路面抗剪环境的单轴贯入试验及局部三轴试验．这些方法可有效比较不同沥青混合料高温性能,获取抗剪参数指标,为评价和预测沥青混凝土路面车辙提供了参数．此外,通过分析重复荷载下沥青混合料蠕变曲线的变化规律,文献[7-8]建立了车辙预估模型,但主要集中于对车辙深度的预测,而对车辙失稳出现时间的研究则相对较少．文献[9]研究表明,沥青混合料的蠕变过程一般会经历初始压密、稳定增长及加速失稳3个阶段．在初始压密阶段,主要表现为沥青混合料内部结构重新调整引起混合料体积变形;稳定增长阶段主要为沥青混合料黏弹塑性累积及内部石料破碎引起混凝土强度降低形成的变形;加速失稳阶段主要为混合料强度失稳导致的变形过大．其中流变次数FN(即第3阶段起始点所对应的荷载作用次数,该点所对应的应变变化率最小)是评价混合料高温稳定性的常用指标．

由于沥青混合料本构的复杂性,其累积变形及失稳过程是多因素作用的结果,涉及材料本构、温度、荷载等多方面因素,采用精确的模型来预测失稳点仍有较大难度．但从沥青混合料蠕变试验可看出,其本质是特定温度、特定荷载作用下沥青混合料蠕变及压剪循环引起的变形累积与变形失稳,因此可基于压剪破坏对这一现象作出解释．为此,本文将通过三轴压缩试验来获取特定温度下沥青混合料的抗剪强度参数,再利用不同围压、加载压应力下沥青混合料三轴动态蠕变曲线得到对应失稳点的流变次数FN,建立表征荷载与失稳点流变次数相关的压剪破坏方程,实现对沥青混合料蠕变失稳点的预测,进一步对预测模型进行验证及参数影响因素研究．

1 材料与试验方法

1.1 材料

试验选用AC13和AC20两种密级配沥青混合料,沥青为等级PG76-22的SBS改性沥青．AC13级配的粗集料为玄武岩,而该级配的细集料及AC20级配的集料则均采用石灰岩．填料均为石灰岩矿粉,粒径小于0.075 mm．原材料相关技术指标均满足规程JTG E20—2011[10]的要求,2种沥青混合料设计级配见表1．AC13和AC20级配沥青混合料油石质量比分别为4.9%和4.4%．

表1 沥青混合料级配

1.2 试验方法与试件成型

三轴试验中材料受力状态与实际路面三向受力状态较为接近,因此本文均采用三轴压缩试验以获取沥青混合料抗剪强度参数,采用三轴动态蠕变试验来研究和预测混合料高温性能及失稳点,其中循环加载波型为加载0.1 s、卸载0.9 s的半正弦波．试验均在万能材料试验机UTM-25中进行,加载前将试件置于空气浴中保温4 h以上,以确保实际加载试件内部均达到试验温度．

试验利用空气压力机加压三轴室内气体,以保证试件所受围压均匀,三轴试验装置如图1所示．试件采用旋转压实仪成型获得尺寸为φ150 mm×170 mm的圆柱形试件,再钻芯得到φ100 mm×150 mm的加载试件,其中每组试验均采用3个平行试件．

图1 三轴试验装置及试样

2 抗剪强度理论与参数

2.1 基本理论

沥青混合料是由强度较高的粒料与黏结力较弱的沥青材料构成的混合体,属于分散体系,根据其颗粒性特征,可认为沥青混合料强度构成源于2方面:① 沥青产生黏结力;② 骨料产生内摩阻力．因此,在对沥青混合料强度构成特性开展研究时,诸多学者普遍采用莫尔-库仑准则作为分析沥青混合料的强度理论,并用黏结力c和内摩擦角φ作为强度理论的分析指标[11]．

通过三轴压缩试验,获得零围压及某一非零围压σ3下的抗压强度σu及σ1,以此做出相应莫尔圆,可得到抗剪强度参数c,φ及破坏面上的抗剪值τ0.此外,假设在三轴动态蠕变试验中,试件在循环荷载σn作用过程中破坏面未发生失稳,则破坏面上剪应力值为τn,如图2所示,抗剪强度参数及破坏面上剪应力值的计算式为

(1)

(2)

(3)

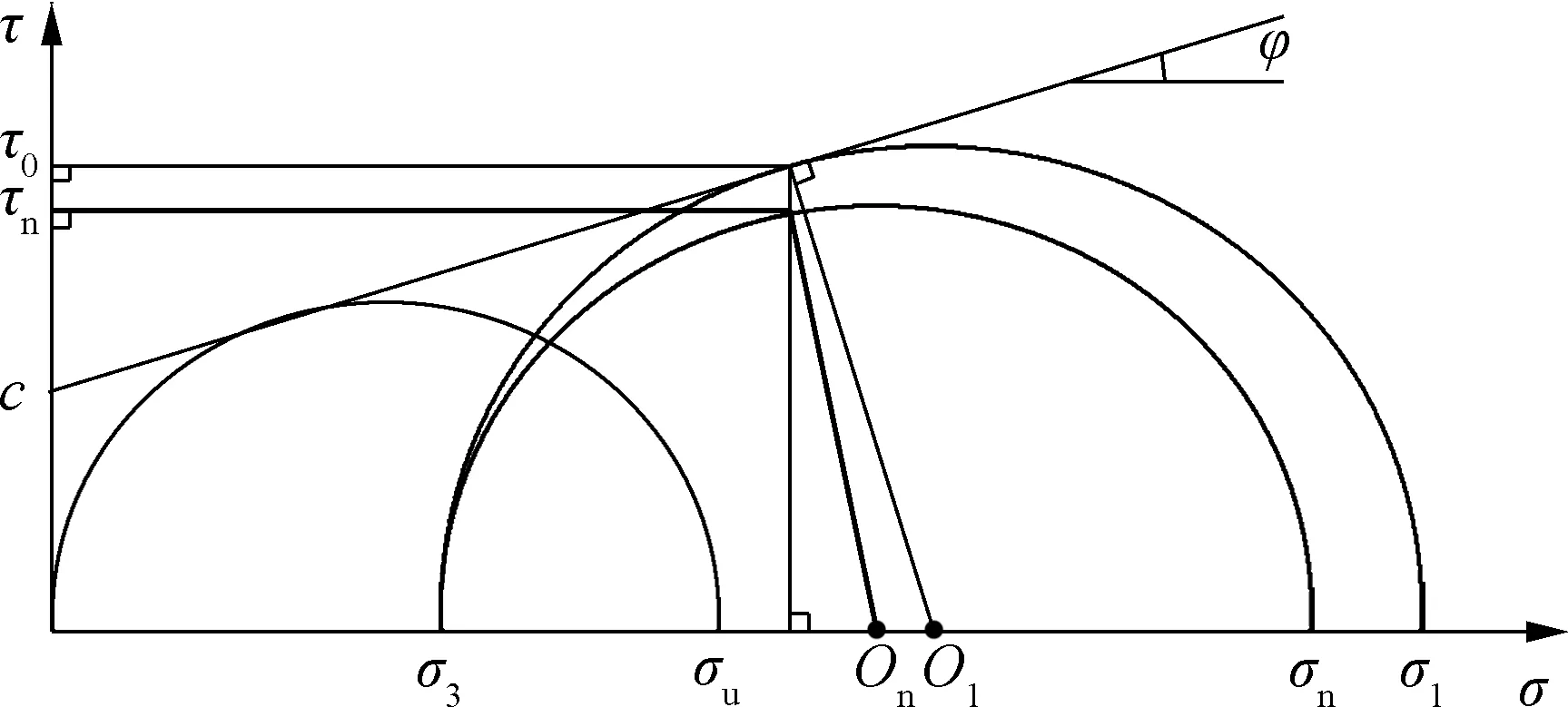
图2 破坏面上剪应力值求解示意图

(4)

式中,σ3为三轴压缩试验中试件所受围压;σ1为非零围压σ3作用下的材料抗压强度;σn为循环荷载,数值小于相同试验条件下的σ1;τ0为三轴受压破坏时破坏面上的剪应力;τn为三轴蠕变试验过程中破坏面上的剪应力．

将式(1)、(2)分别代入到式(3)、(4)中,消去中间变量,可得

(5)

(6)

即τ0与τn和抗剪强度参数c，φ值及混合料受力状态相关．

2.2 抗剪强度参数

设定温度为60 ℃,围压分别为0,69,138 kPa,对AC13及AC20级配沥青混合料分别进行三轴压缩破坏试验．基于莫尔-库伦破坏准则,获得各围压下的莫尔圆,并根据零围压及任意非零围压下的莫尔圆组合得到相应抗剪强度参数c,φ,取均值用于后续研究．试验结果如表2所示．

表2 三轴压缩试验结果

3 三轴动态蠕变试验结果及失稳点预测模型

3.1 流变次数FN合理性分析

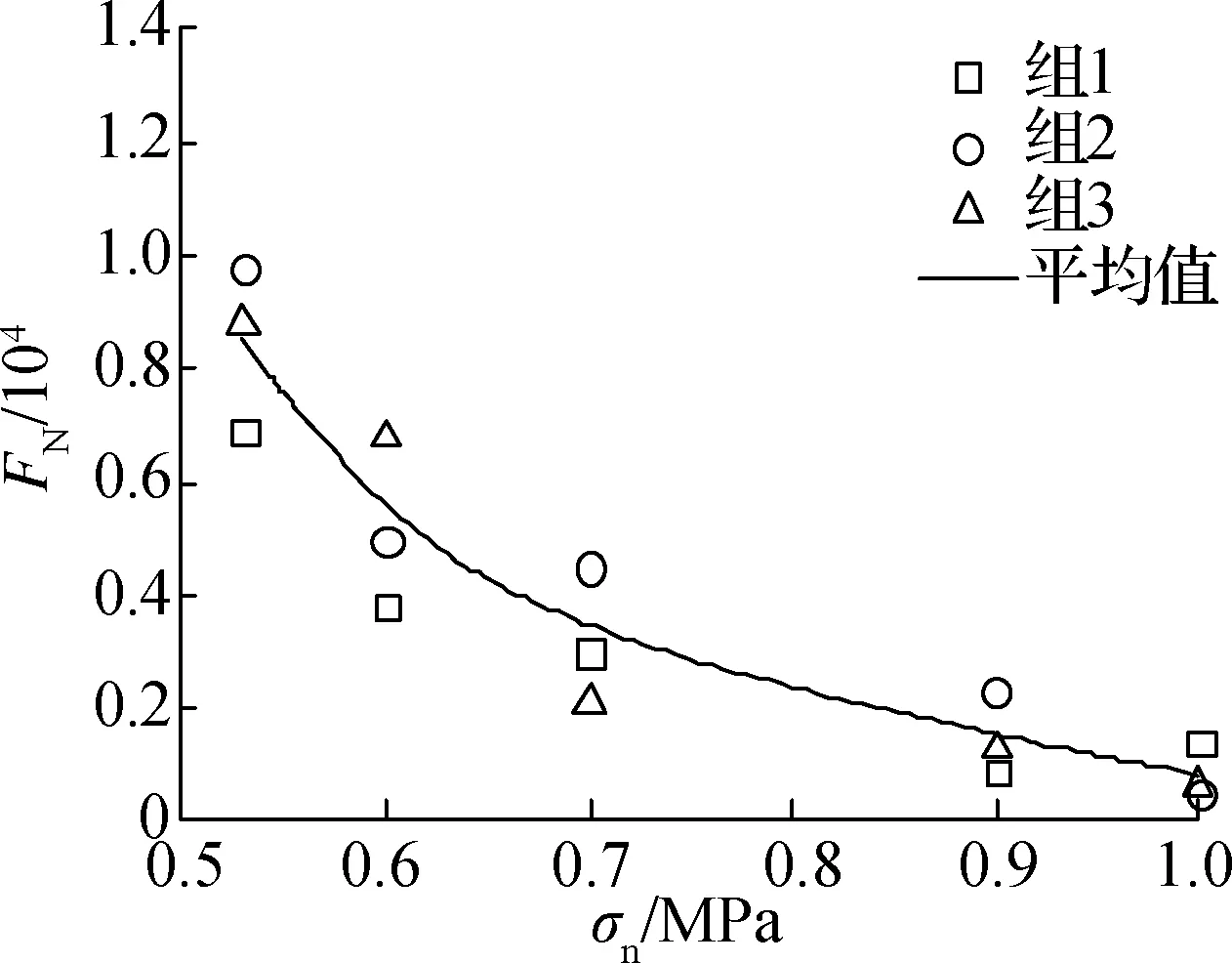
基于表2中AC13混合料的试验结果,在各围压下分别设置小于对应抗压强度值的5个压应力载荷σn,分别进行三轴动态蠕变试验,各围压下分别进行3组试验(组1,组2和组3)．由此可获得材料应变与循环加载数之间的关系,即蠕变曲线,进而可利用该曲线获得材料失稳点所对应的流变次数FN,即材料破坏的寿命,结果如图3所示．

由图3可知,围压值相同时,随荷载增加,FN值呈指数下降;当荷载相同时,如压应力σn为0.9 MPa时,围压越大,混合料试验所获得的FN值越大,即寿命越长,此时相对于围压0,69和138 kPa下试件FN值分别增加了约73.3%和333.3%．

根据15个试件失稳点对应的FN试验结果作图,如图4所示.由图可见,FN值均位于2倍安全因子分散带内,这说明试验所得的FN值较为合理[12]．与此同时,试件所受的压应力σn越大,数据的离散性也相对越大;而随着σn的逐渐减小,FN值也越接近中值线,即离散性也越小.总体而言，数据用于循环破坏分析是合理的．

3.2 流变次数FN预测模型

取三轴动态蠕变试验所得的流变次数FN的均值(即2倍安全因子分散带的中值)作为60 ℃时混合料寿命进行分析,进一步从压剪破坏角度对不同应力水平下混合料变形失稳开展研究,其中破坏面上剪应力值τn可通过式(6)得到,c,φ值的试验结果见表2．

(a) 围压0 kPa

(b) 围压69 kPa

(c) 围压138 kPa

图3AC13级配沥青混合料流变次数FN试验结果

由图5(a)可知,对同种沥青混合料,围压一定时,随τn值的减小,FN值呈指数上升趋势,在τn值减小到一定程度时，FN趋于无穷,且围压值越大,沥青混合料寿命越长，破坏极限剪应力值越大．

为得到较为统一的失稳预估模型,将混合料在某一围压下三轴动态蠕变试验和压缩试验所得破坏面上的剪应力比值τn/τ0作为变形曲线的x轴,对应的循环加载所得流变次数FN作为y轴,可得到消除围压影响的寿命曲线,如图5(b)所示．

选用以下指数函数模型来反映图5(b)的变化规律:

(7)

式中,a,b为待求参数．τn和τ0可分别通过式(5)、(6)计算得到．

(a) 围压0 kPa

(b) 围压69 kPa

(c) 围压138 kPa

图4AC13沥青混合料流变次数FN两倍安全因子分散带

通过拟合试验结果，得到AC13沥青混合料变形失稳点的预估模型,即

(8)

其中,a=550.541 420,b=-4.851 116．

3.3FN预测模型的验证

在实际工程中,为增加沥青路面上层材料的高温稳定性,通常在沥青混合料中加入一定比例的添加剂,如纤维和抗车辙剂[13]．增加添加剂可改变沥青胶结料的性能,增强其黏结能力,从而使得混合料抗剪强度参数c增大．而沥青混合料内摩擦角φ不仅与集料间的摩擦有关,还受集料与沥青间的黏

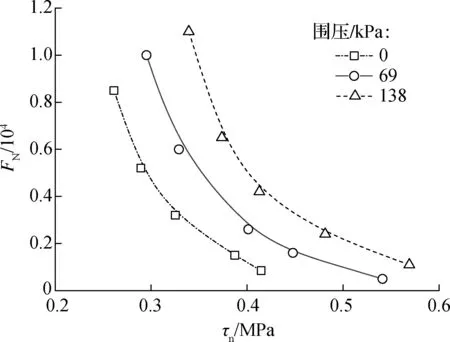
(a)τn-FN曲线

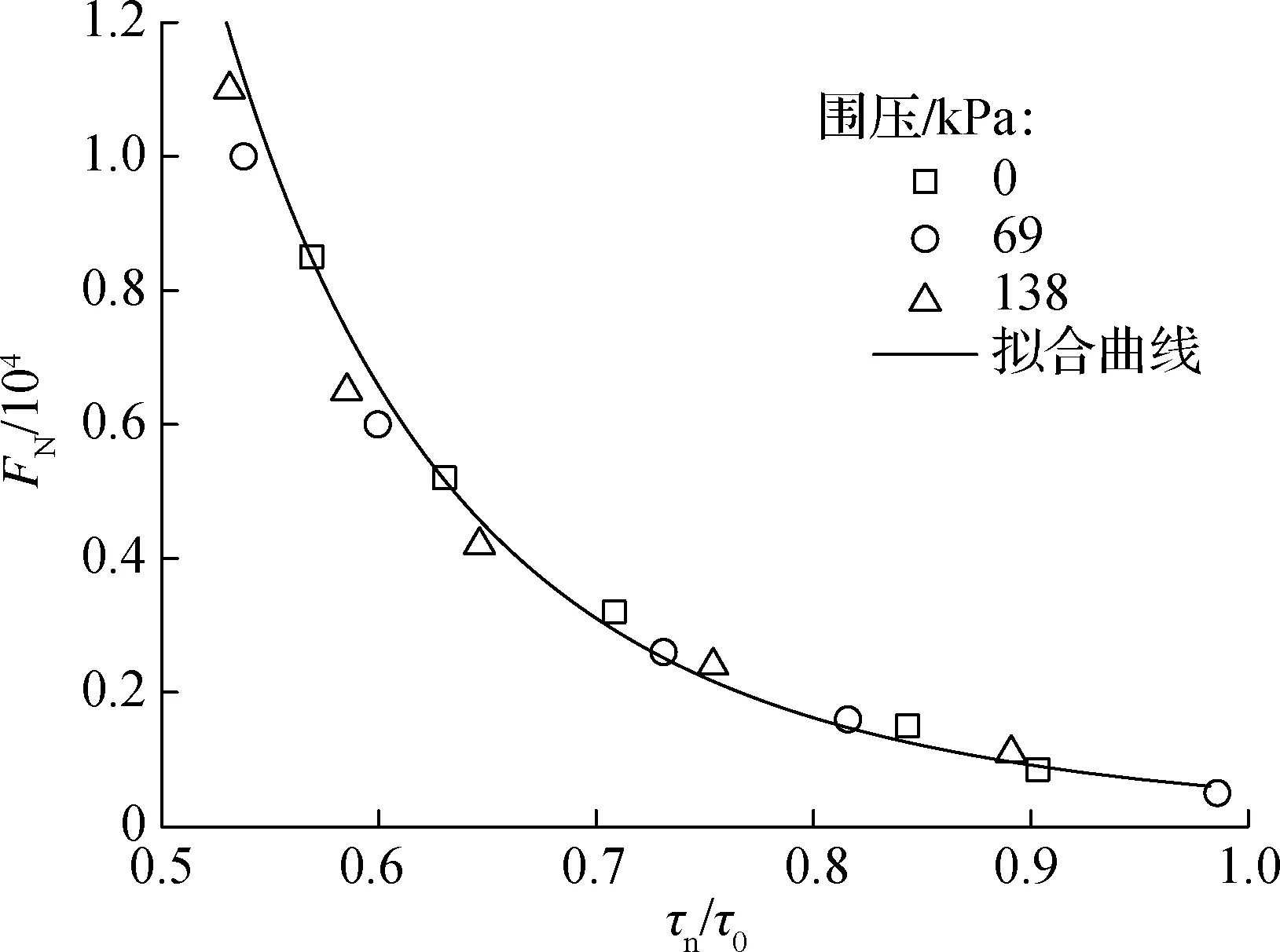
(b)τn/τ0-FN曲线

图5AC13沥青混合料流变次数FN变化曲线

结力影响,随黏结力c增大,φ也增大．级配未改变时,只需测出模型中的c,φ值,并在某一围压下根据循环加载值σn,利用式(5)和(6)就可得到模型(8)的剪应力比值τn/τ0,进而可通过模型(8)预测对应受力状态下失稳点的FN值．

本文在AC13级配混合料中分别加入质量分数为0.4%和0.3%的抗车辙剂Domix和玄武岩纤维,在60 ℃下对FN值的预测模型(8)进行验证．通过三轴压缩试验后,分别获得抗剪参数值,见表3.其中，AC13-DX表示在混合料中加入质量分数为0.4%抗车辙剂Domix;AC13-BF表示在混合料中加入质量分数为0.3%玄武岩纤维．在138 kPa围压下,对2种混合料进行压应力载荷σn分别为0.9,1.0,1.2,1.5 MPa的三轴动态蠕变试验，以此来验证模型预测结果的合理性．

由图6(a)可知,FN试验值与模型预测值变化规律一致．图6(b)表明,试验结果均在预测值的2倍因子分散带内,说明预测模型是合理的.因此本模型可对混合料失稳点出现的时间进行有效预测．同时也说明温度相同时,胶结料性质的改变主要体现在c,φ值上,即在模型剪应力比τn/τ0中得以反映,对模型参数a和b的影响可忽略．

表3 含添加剂AC13沥青混合料三轴压缩试验结果

4 模型参数影响因素分析

由上述研究可知,试验温度相同时,在沥青混合料中加入纤维或抗车辙剂后,胶结料性质发生改变,对模型的影响主要与剪应力比值有关,与a，b的取值无关．为进一步研究对模型参数a和b的影响因素,本文分别改变了混合料级配及试验温度,利用上述相同方法获得相应预测模型．

4.1 级配类型

通过三轴受压破坏试验获得温度为60 ℃,围压分别为0,69,138 kPa的AC20级配沥青混合料抗压强度值,见表2．以此结果为基础,在围压138 kPa下,设置小于对应抗压强度值的5个压应力值σn分别进行三轴动态蠕变试验.与AC13沥青混合料的试验方法相同,在获得材料失稳点所对应的流变次数FN后，取FN的均值,即2倍安全因子分散带的中值作为该温度下试件的寿命,试验结果如图7(a)所示．由图可知,对于AC20级配沥青混合料,在138 kPa围压下随破坏面上剪应力值τn的减小,流变次数FN呈指数上升趋势,并在τn减小到一定程度时趋于无穷.对比同一围压下2种沥青混合料的τn-FN曲线可知,在剪应力值τn相同时,AC20级配沥青混合料的寿命要明显小于AC13级配混合料的寿命,破坏极限剪应力值也相对较小．

类似于AC13混合料的处理方法,利用指数函数模型(7)拟合图7(b)中的点，可得到相应的变形曲线.AC20沥青混合料的变形失稳点的预估模型为

(9)

式中,a=263.488 930,b=-5.739 202．

由图7(b)可知,在剪应力比τn/τ0相同时,AC13级配沥青混合料寿命相对较好，破坏极限也相对较高．对比预测模型(8)和(9)可知,参数a,b值发生了明显改变,相对于AC13级配,AC20级配沥青混合料预测模型参数a，b值分别减小了52.1%和18.3%,因此级配对模型参数的影响不可忽略．

4.2 温度

通过三轴受压破坏试验获得温度分别为40,50,70 ℃,围压分别为0,69,138 kPa时,AC13级配沥青混合料的抗压强度值,见表4．以此结果为基础,在围压0 kPa下,设置小于对应抗压强度值的多个压应力值σn,分别进行三轴动态蠕变试验.与前述试验方法相同，先获得材料失稳点对应的流变次数FN,并对其合理性进行分析,取2倍安全因子分散带的中值来拟合τn/τ0-FN曲线,如图8(a)所示．

(a) τn-FN曲线

(b) τn/τ0-FN曲线

表4 不同温度下AC13级配混合料三轴压缩试验结果

(a)τn/τ0-FN曲线

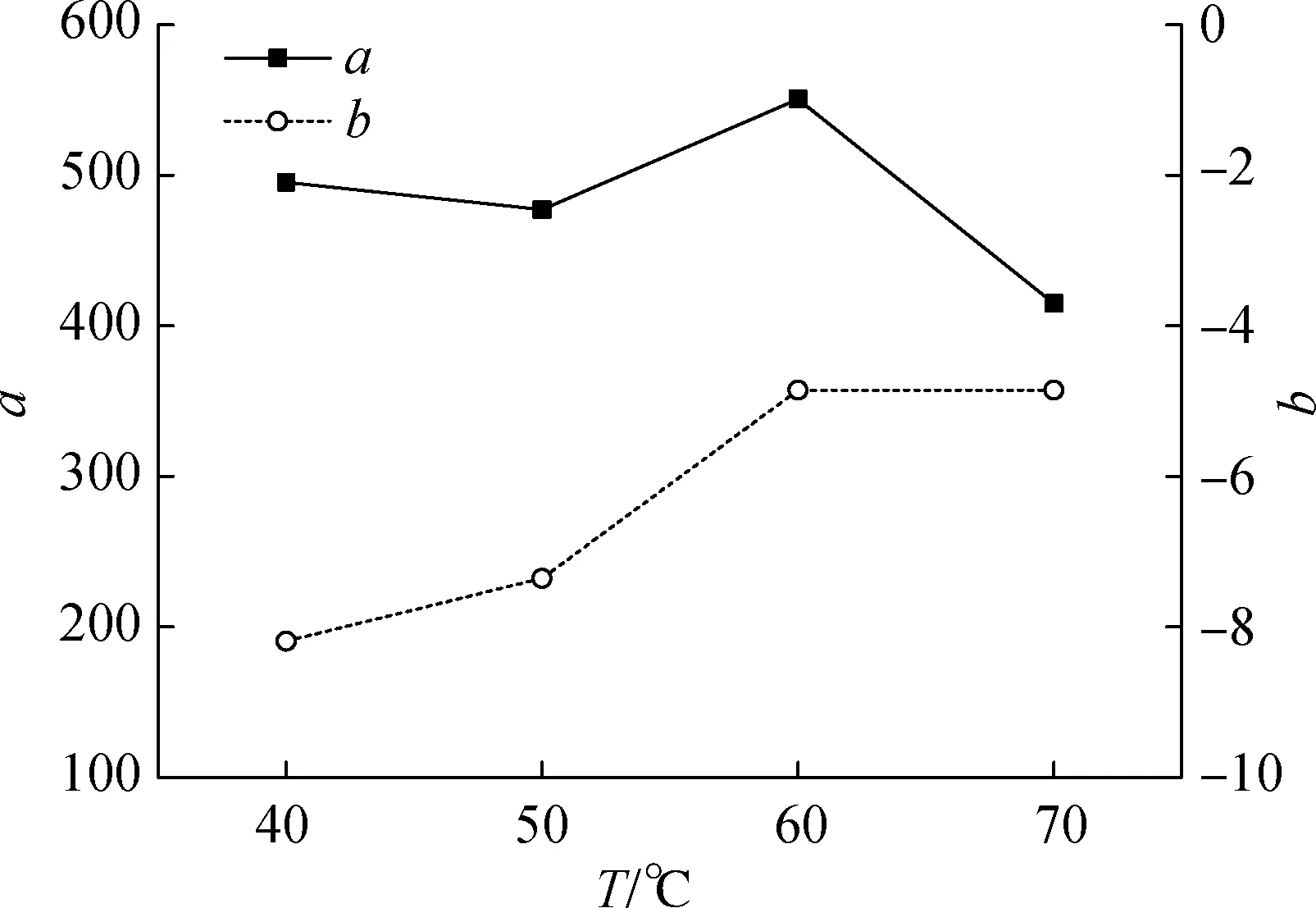
(b) 预测模型参数的变化情况

图8温度对AC13级配沥青混合料预测模型的影响

由图8(a)可知,当剪应力比值τn/τ0较大时,温度对流变次数FN值的影响较小;随τn/τ0的减小,温度越低,混合料的寿命越长,破坏极限也越大．混合料在40 ℃的破坏极限相较70 ℃提高了近37.5%．因此温度对沥青混合料失稳点预测模型参数的影响较大,利用指数函数模型(7)拟合各温度下试验结果所得的a和b值如图8(b)所示．

5 结论

1) 通过研究AC13级配沥青混合料在60 ℃下高温蠕变的变化规律,建立了破坏面上剪应力比值与流变次数FN相关的预测模型,并利用含纤维及抗车辙剂的同级配沥青混合料的试验,验证了预测模型的合理性．

2) 仅改变沥青混合料胶结料的性能,如加入添加剂,不会对预测模型中参数a和b产生明显影响;而改变沥青混合料的级配及试验温度,均会对预测模型参数a和b值产生较大影响．

3) 相对于AC13级配,AC20级配沥青混合料在60 ℃下的预测模型参数a，b值分别减小了52.1%和18.3%;而随着温度的升高,AC13级配沥青混合料预测模型参数a整体呈现波动趋势,b则呈现增长趋势．

References)

[1] 王辉, 李雪连, 张起森. 高温重载作用下沥青路面车辙研究[J]. 土木工程学报, 2009, 42(5): 139-144. Wang Hui, Li Xuelian, Zhang Qisen. Rutting in asphalt pavement under heavy load and high temperature [J].ChinaCivilEngineeringJournal, 2009,42(5): 139-144. (in Chinese)

[2] Cao X, Tang B, Zhu H, et al. Cooling principle analyses and performance evaluation of heat-reflective coating for asphalt pavement [J].JournalofMaterialsinCivilEngineering, 2011,23(7): 1067-1075. DOI:10.1061/(asce)mt.1943-5533.0000256.

[3] 朱浩然, 杨军, 陈志伟. 沥青混合料抗剪性能的三轴剪切试验[J]. 交通运输工程学报, 2009, 9(3): 19-23. Zhu Haoran, Yang Jun, Chen Zhiwei. Triaxial shear test on anti-shear properties of asphalt mixture [J].JournalofTrafficandTransportationEngineering, 2009,9(3): 19-23. (in Chinese)

[4] Goh S W, You Z. A simple stepwise method to determine and evaluate the initiation of tertiary flow for asphalt mixtures under dynamic creep test [J].ConstructionandBuildingMaterials, 2009,23(11): 3398-3405. DOI:10.1016/j.conbuildmat.2009.06.020.

[5] 毕玉峰, 孙立军. 沥青混合料抗剪试验方法研究[J]. 同济大学学报 (自然科学版), 2005, 33(8): 1036-1040. DOI:10.3321/j.issn:0253-374X.2005.08.009. Bi Yufeng, Sun Lijun. Research on test method of asphalt mixture’s shearing properties [J].JournalofTongjiUniversity(NaturalScience), 2005,33(8): 1036-1040. DOI:10.3321/j.issn:0253-374X.2005.08.009.(in Chinese)

[6] 黄晓明, 张裕卿. 沥青混合料高温性能试验方法[J]. 公路交通科技, 2008, 25(5): 1-7,12. DOI:10.3969/j.issn.1002-0268.2008.05.001. Huang Xiaoming, Zhang Yuqing. A test design for high-temperature performance of asphalt mixtures [J].JournalofHighwayandTransportationResearchandDevelopment, 2008,25(5): 1-7,12. DOI:10.3969/j.issn.1002-0268.2008.05.001. (in Chinese)

[7] Li Q, Ni F, Gao L, et al. Evaluating the rutting resistance of asphalt mixtures using an advanced repeated load permanent deformation test under field conditions [J].ConstructionandBuildingMaterials, 2014,61: 241-251. DOI:10.1016/j.conbuildmat.2014.02.052.

[8] Fontes L P T L, Triches G, Pais J C, et al. Evaluating permanent deformation in asphalt rubber mixtures [J].ConstructionandBuildingMaterials, 2010,24(7): 1193-1200. DOI:10.1016/j.conbuildmat.2009.12.021.

[9] 张久鹏, 黄晓明, 李辉. 重复荷载作用下沥青混合料的永久变形[J]. 东南大学学报 (自然科学版), 2008, 38(3): 511-515. DOI:10.3321/j.issn:1001-0505.2008.03.029. Zhang Jiupeng, Huang Xiaoming, Li Hui. Permanent deformation of asphalt mixture under repeated load [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2008,38(3): 511-515. DOI:10.3321/j.issn:1001-0505.2008.03.029. (in Chinese)

[10] 交通运输部公路科学研究院．JTG E20—2011 公路工程沥青及沥青混合料试验规程[S].北京:人民交通出版社,2011.

[11] Bai Y, Wierzbicki T. Application of extended mohr-Coulomb criterion to ductile fracture [J].InternationalJournalofFracture, 2010,161(1): 1-20. DOI:10.1007/s10704-009-9422-8.

[12] 丁智平, 陈吉平, 尹泽勇, 等. 镍基单晶合金复杂应力状态低周疲劳寿命预测[J]. 稀有金属材料与工程, 2006, 35(10): 1548-1553. DOI:10.3321/j.issn:1002-185X.2006.10.009. Ding Zhiping, Chen Jiping, Yin Zeyong, et al. Low cycle fatigue life prediction for single crystal nickel-based superalloy [J].RareMetalMaterialsandEngineering, 2006,35(10): 1548-1553. DOI:10.3321/j.issn:1002-185X.2006.10.009. (in Chinese)

[13] Zhang X, Gu X, Lv J, et al. 3D numerical model to investigate the rheological properties of basalt fiber reinforced asphalt-like materials [J].ConstructionandBuildingMaterials, 2017,138: 185-194. DOI:10.1016/j.conbuildmat.2017.01.110.

Predictionmodelsofcreepinstabilitypointsforasphalt
mixturesathightemperatureandparameterseffectsonmodel

Gu Xingyu1Lü Junxiu1Zhang Xiaoyuan1Zou Xiaoyong2

(1School of Transportation, Southeast University, Nanjing 210096,China)
(2Jinhua Highway Administration Bureau, Jinhua 321103, China)

U416.217

A

1001-0505(2017)05-1013-07

2017-03-03.

顾兴宇(1976—),男,博士,副教授,博士生导师,guxingyu1976@163.com．

国家自然科学基金资助项目 (51108082)．

顾兴宇,吕俊秀,张小元,等.沥青混合料高温蠕变失稳点预测模型及参数影响[J].东南大学学报(自然科学版),2017,47(5):1013-1019.

10.3969/j.issn.1001-0505.2017.05.027.

10.3969/j.issn.1001-0505.2017.05.027