基于图像加权的多能光子计数X线CT全能谱图像重建改进方法

周正东 管绍林 涂佳丽 李剑波 张雯雯

(南京航空航天大学核科学与工程系, 南京 210016)

基于图像加权的多能光子计数X线CT全能谱图像重建改进方法

周正东 管绍林 涂佳丽 李剑波 张雯雯

(南京航空航天大学核科学与工程系, 南京 210016)

为了提高基于图像加权的多能光子计数X线CT全能谱重建图像的质量,提出了一种图像重建改进方法．首先,对每个能量段的投影数据采用最大后验概率(MAP)统计重建算法进行图像重建;然后,对各能量段图像进行优化加权求和,获得全能谱图像．仿真实验结果表明,MAP统计重建算法可显著提高全能谱重建图像的对比噪声比(CNR)．与滤波反投影算法相比,当能量段数分别为2,4,6,9时,MAP统计重建算法使得钙图像的CNR分别提高659.7%,643.4%,621.2%,586.1%,碘图像的CNR分别提高663.8%,648.6%,635.1%,600.9%,软组织图像的CNR分别提高596.2%,638.5%,592.6%,596.3%;与能量积分法相比,当能量段数分别为2,4,6,9时,MAP统计重建算法使得钙图像的CNR分别提高43.3%,49.1%,49.3%,44.5%,碘图像的CNR分别提高43.2%,45.7%,45.7%,40.2%,软组织图像的CNR分别提高21.5%,28.9%,25.5%,26.2%．

光子计数X线CT; 基于图像加权; 最大后验概率; 对比噪声比

Abstract: To improve the full spectral reconstruction image quality for the image-based weighting multi-energy photon counting X-ray computed tomography (CT), an improved image reconstruction method was proposed. First, the maximum a posteriori probability (MAP) statistical reconstruction algorithm was used to reconstruct the image in each energy bin. Then, the images from each energy bin were summarized with optimal weights to obtain the full spectral image. The simulation experimental results demonstrate that the MAP statistical reconstruction algorithm can significantly improve the contrast-to-noise ratio(CNR) of the full spectral reconstruction image. Compared with the filtered back projection (FBP) algorithm, for the cases with the energy spectrum split into 2, 4, 6 and 9 bins, the MAP statistical reconstruction algorithm can offer the CNR improvement up to 659.7%, 643.4%, 621.2% and 586.1%for calcium,663.8%, 648.6%, 635.1% and 600.9% for iodine, 596.2%, 638.5%,592.6% and 596.3% for soft tissue, respectively.Compared with the energy-integrating method,for the energy-resolved cases with 2, 4, 6 and 9 energy bins, the MAP statistical reconstruction algorithm can offer the CNR improvement up to 43.3%, 49.1%, 49.3% and 44.5% for calcium, 43.2%, 45.7%, 45.7% and 40.2% for iodine, 21.5%, 28.9%, 25.5% and 26.2% for soft tissue,respectively.

Keywords: photon counting X-ray computed tomography (CT); image-based weighting; maximum a posteriori probability(MAP); contrast-to-noise ratio(CNR)

传统X线CT系统利用电荷积分探测器进行信号检测,光子权重与其能量成正比,较高能量的光子被赋予较大的权重．然而,重建图像的对比度主要取决于较低能量的光子,因此电荷积分探测方式将导致重建图像对比度下降[1-2]．近期研发的光子计数探测器具有能量分辨能力,它由半导体探测器及快速专用集成电路组成,在医学诊断X线能量范围内具有较高的量子效率,可灵活设置能量阈值,并可消除低能电子学噪声的干扰,通过对被检物体的一次扫描可以同时获得多个能量段的光子计数[3]．为了提高重建图像质量,Schmidt[4]根据每个能量段图像中对比材料和背景材料衰减系数差异构造权重,然后将权重赋予每个能量段图像进行加权求和,得到全能谱重建图像,这种方法被称为图像加权成像法．

利用图像加权方法来提高基于光子计数探测器X线CT重建图像质量已成为当前的研究热点之一．Kalluri等[5]和Berglund等[6]对乳腺模型进行了图像加权重建研究,实验结果表明,与传统的能量积分成像方法相比,该方法所得的重建图像质量得到较大改善．针对能量分段数量对重建图像质量影响的研究表明,在一定能量分段数量范围内,图像的对比噪声比随能量分段数量增加而增加,达到某一能量分段数量后,对比噪声比的增加幅度减小[2,7-9]．上述研究均利用解析重建算法对每个能量段内的投影数据进行图像重建,但对于低剂量成像以及能量分段数较多的情况,每个能量段内的光子数将显著减少,信噪比将会同步下降,导致重建图像质量下降．采用统计重建算法则可以有效克服这些缺点．本文利用最大后验概率算法[10-11]对每个能量段内的投影数据进行重建,然后对各能量段的图像进行优化加权,得到全能谱重建图像,并定量评价了该方法的图像重建性能．

1 材料与方法

1.1 模拟实验装置

采用Geant4软件对多能光子计数X线CT系统进行模拟．Geant4模拟软件是一个开源的软件包,采用C++语言编写,能够精确仿真粒子与物质相互作用的整个过程．仿真用光子计数探测器设为线性等距探测器,包含190个探测单元,每个单元长度为0.8 mm,其材料为密度5.85 g/cm3的碲锌镉(cadmium zinc telluride,CZT)．模拟探测器被视为理想探测器,能够探测所有透射目标后的光子．实验采用扇形角为8.6°的X线源,其能谱由TASMIC工具包生成,其中管电压设为100 kV,采用厚度为0.8 mm的铍和10 mm的铝作为过滤器,以滤除低能X线,减少低能辐射损伤[12]．在X线CT模拟系统中,射线源到模体中心的距离设为670 mm,源到探测器的距离设为1 010 mm．受照目标为圆柱形模体,模体的几何参数、材料组成以及横切面如表1和图1所示．仿真过程中,每次扫描发射的光子数为2×106,角采样间隔为1°,能量分段数t分别设为2,4,6,9,光子计数探测器的低能阈值设为20 keV,各能量分段数对应的能量段范围如表2所示．

表1 模体几何参数和组成成分

1.2 基于图像加权的全能谱图像重建算法

1.2.1 MAP统计重建算法

实际探测器单元测量到的光子计数具有统计特性．MAP统计重建算法以泊松模型模拟投影数据的获取过程[13],即

(1)

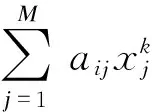
(2)

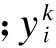
MAP统计重建算法的过程是根据泊松模型,通过一组测量投影值y,找出一组x使得条件概率P(xy)最大．计算公式为[14]

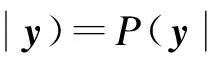
(3)

式中,P(x)为图像的先验知识,一般采用Gibbs先验分布函数,其表达式为[14]

P(x)=exp(-βU(x))/q

(4)

(5)

式中,β和q为常数;U(x)为能量函数;Nj为所选像素j的邻域;xj为像素j的像素值;xr为与像素j相邻的像素r的像素值;wjr表示像素j和像素r之间的相互作用程度,常用的一种计算方法是以像素j和像素r之间距离的倒数来表示[15]．

通常将式(3)取对数,以作为目标函数进行最大化优化,即[14]

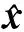
(6)

1.2.2 图像加权成像

图像加权成像首先对单个能量段的投影数据进行图像重建，然后对各个能量段图像进行优化加权，获得全能谱图像.各能量段的重建图像对最终图像质量的贡献不同，赋予各能量段图像的权重也不同，可表示为[4]

(7)

式中,K为能量段总数;wk为第k能量段图像的权重．全能谱重建图像的对比噪声比可由各个能量段图像对比噪声比表示[4],即

(8)

对式(8)求关于第n(n=1,2,…,K)个能量段图像权重wn的偏导数,可得到对比噪声比最大时的归一化权重wn为[4]

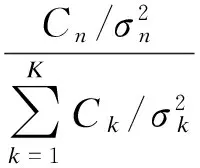
(9)

式(9)中的分子和分母分别表示每个能量段重建图像的对比噪声方差比和各能量段重建图像对比噪声方差比之和．

1.3 重建图像质量评价

全能谱重建图像质量利用对比噪声比进行定量分析,其表示式为

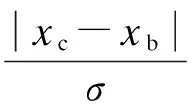
(10)

式中,xc和xb分别为重建图像中对比材料和背景材料的平均像素值;σ为重建图像的噪声水平,且

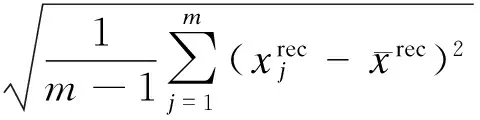
(11)

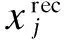
2 实验结果与分析

2.1 各能量段重建图像性能评价

当能量分段数t=2,4,6,9时,采用FBP算法和MAP统计重建算法重建各能量分段的图像,并计算对比噪声比．图2为各能量段重建图像中3种对比材料图像的对比噪声比．由图可知,低能量段的图像对比噪声比相对较高,高能量段的图像对比噪声比相对较低．随着能量段光子能量的增加,重建能量段图像的对比噪声比逐渐减少．在相同的能量分段数下,MAP统计重建算法重建各能量段图像的对比噪声比明显高于FBP算法．

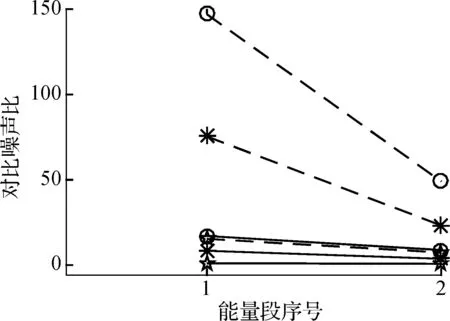
(a) t=2

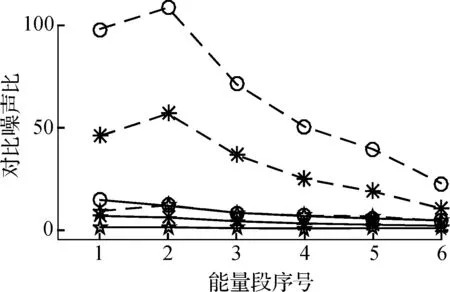
(c) t=6

图2各能量段重建图像中3种对比材料图像的对比噪声比

2.2 全能谱重建图像性能评价

图3(a)为能量积分(即不对光子能谱进行能量分段,t=1)情况下的FBP重建图像;图3(b)～(e)为t=2,4,6,9时采用FBP算法获得的图像加权优化全能谱重建图像．与能量积分情况下的FBP重建图像相比,基于图像加权优化获得的全能谱图像质量较好．图4(a)为能量积分情况下的MAP重建图像;图4(b)～(e)为t=2,4,6,9时采用MAP统计重建算法获得的图像加权优化全能谱重建图像．由图3和图4可以看出,与FBP算法相比,MAP统计重建算法有效克服了重建图像中的噪声,图像质量较好．

图3 FBP算法重建的不同能量段数目下的全能谱图像

图4 MAP统计重建算法重建的不同能量段数目下全能谱图像

各能量段数目下FBP算法重建全能谱图像中3种对比材料图像的对比噪声比Rf,MAP统计重建算法重建全能谱图像中3种对比材料图像的对比噪声比Rm以及MAP重建图像对比噪声比相对于FBP重建图像的提升幅度Ri见表3．图5给出了不同能量段数目下FBP算法及MAP统计重建算法重建全能谱图像中对比材料图像的对比噪声比变化曲线．由表3可以看出,与FBP算法相比,对于能量分段数t分别为2,4,6,9的情况,MAP统计重建算法使得重建全能谱图像中钙材料图像的CNR分别提高了659.7%,643.4%,621.2%,586.1%,碘材料图像的CNR分别提高了663.8%,648.6%,635.1%,600.9%,软组织材料图像的CNR分别提高了596.2%,638.5%,592.6%,596.3%;MAP统计重建算法使得重建全能谱图像中钙材料图像的CNR分别提高了43.3%,49.1%,49.3%,44.5%,碘材料图像的CNR分别提高了43.2%,45.7%,45.7%,40.2%,软组织材料图像的CNR分别提高了21.5%,28.9%,25.5%,26.2%．由表3和图5还可以看出,与能量积分情况下的重建图像相比,无论是采用FBP算法还是MAP统计重建算法,基于图像加权的全能谱重建图像的对比噪声比均得到了提升;与FBP算法相比,MAP统计重建算法使得全能谱重建图像的对比噪声比显著提升,随着能量分段数的增加,重建图像的对比噪声比趋于稳定．

3 结论

1) 在图像加权多能光子计数X线CT图像重建中,对于低剂量成像以及能量分段数较多的情况,每个能量段内收集的光子数减少,信噪比较小,利用解析重建算法难以获得高质量图像．MAP统计重建算法充分考虑了投影数据的统计特性,在重建过程中施加了先验知识分布,同时图像加权重建在构造权重时考虑了每个能量段图像的对比噪声比,因此全能谱重建图像质量可获得有效提升．

表3 重建全能谱图像中对比材料在各能量段数下的CNR值

图5重建全能谱图像中对比材料CNR值随能量段数的变化

2)仿真实验结果表明,利用MAP统计重建算法可显著提高图像的对比噪声比,随着能量分段数的增加,全能谱重建图像的对比噪声比趋于稳定．

3)在后续的研究中,考虑将本文提出的方法进一步应用于基于多能光子计数X线CT的物质识别研究中,有望提高物质的识别精度．

References)

[1] Sossin A, Rebuffel V, Tabary J, et al. A novel scatter separation method for multi-energy X-ray imaging[J].PhysicsinMedicine&Biology, 2016,61(12):4711-4728. DOI:10.1088/0031-9155/61/12/4711.

[2] Lee S W, Choi Y N, Cho H M, et al. A Monte Carlo simulation study of the effect of energy windows in computed tomography images based on an energy-resolved photon counting detector[J].PhysicsinMedicine&Biology, 2012,57(15):4931-4949. DOI:10.1088/0031-9155/57/15/4931.

[3] Schmidt T G. CT energy weighting in the presence of scatter and limited energy resolution[J].MedicalPhysics, 2010,37(3):1056-1067. DOI:10.1118/1.3301615.

[4] Schmidt T G. Optimal “image-based” weighting for energy-resolved CT[J].MedicalPhysics, 2009,36(7):3018-3027. DOI:10.1118/1.3148535.

[5] Kalluri K S, Mahd M, Glick S J. Investigation of energy weighting using an energy discriminating photon counting detector for breast CT[J].MedicalPhysics, 2013,40(8):081923. DOI:10.1118/1.4813901.

[6] Berglund J, Johansson H, Maack H I, et al. Energy weighting improves the image quality of spectral mammograms: Implementation on a photon-counting mammography system[C]//SPIEMedicalImaging. San Diego, CA, USA, 2014:90331. DOI:10.1117/12.2042238.

[7] Choi Y N, Lee Y J, Kim H J. The effect of energy weighting on X-ray imaging based on photon counting detector: A Monte Carlo simulation[J].ProceedingofSPIE, 2012,8313(2):193. DOI:10.1117/12.910845.

[8] Rupcich F, Gilat-Schmidt T. Experimental study of optimal energy weighting in energy-resolved CT using a CZT detector[C]//SPIEMedicalImaging. Lake Buena Vista, Florida, USA, 2013:303-311. DOI:10.1117/12.2008439.

[9] Lee Y, Lee S, Kim H J. Comparison of spectral CT imaging methods based a photon-counting detector: Experimental study[J].NuclearInstrumentsandMethodsinPhysicsResearchSectionA:Accelerators,Spectrometers,DetectorsandAssociatedEquipment, 2016,815: 68-74. DOI:10.1016/j.nima.2016.01.069.

[10] Ansari A, Danyali H, Helfroush M S. HS remote sensing image restoration using fusion with MS images by EM algorithm[J].IETSignalProcessing, 2017,11(1): 95-103. DOI:10.1049/iet-spr.2016.0141.

[11] Helin T, Burger M. Maximum a posteriori probability estimates in infinite-dimensional Bayesian inverse problems[J].InverseProblems, 2015,31(8): 085009. DOI:10.1088/0266-5611/31/8/085009.

[12] Punnoose J, Xu J, Sisniega A, et al. Technical note: Spektr 3.0—A computational tool for X-ray spectrum modeling and analysis[J].MedicalPhysics, 2016,43(8):4711-4717. DOI:10.1118/1.4955438.

[13] Caldeira L, Scheins J J, Almeida P, et al. Maximum a posteriori reconstruction using PRESTO and PET/MR data acquired simultaneously with the 3TMR-BrainPET[J].NuclearScienceSymposiumConferenceRecord, 2010,612(3):2879-2884. DOI:10.1109/nssmic.2010.5874322.

[14] Chen Y, Ma J, Feng Q, et al. Nonlocal prior Bayesian tomographic reconstruction[J].JournalofMathematicalImagingandVision, 2008,30(2):133-146. DOI:10.1007/s10851-007-0042-5.

[15] 刘祎, 桂志国, 张权, 等. 一种基于指数型先验分布的正电子发射断层图像重建算法[J]. 中国组织工程研究与临床康复, 2010, 14(52): 9760-9763. DOI:10.3969/j.issn.1673-8225.2010.52.018. Liu Yi, Gui Zhiguo, Zhang Quan, et al. Positron emission tomography image reconstruction algorithm based on an exponential Markov random field prior model[J].JournalofClinicalRehabilitativeTissueEngineeringResearch, 2010,14(52): 9760-9763. DOI:10.3969/j.issn.1673-8225.2010.52.018.(in Chinese)

Improvedimage-basedweightingmethodforfullspectralimagereconstructionofmulti-energyphotoncountingX-rayCT

Zhou Zhengdong Guan Shaolin Tu Jiali Li Jianbo Zhang Wenwen

(Department of Nuclear Science and Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

TP391

A

1001-0505(2017)05-0892-05

2017-04-02.

周正东(1969—),男,博士,副教授,zzd_msc@nuaa.edu.cn.

国家自然科学基金资助项目(51575256)、中央高校基本科研业务费专项资金资助项目(NZ2016102).

周正东,管绍林,涂佳丽，等.基于图像加权的多能光子计数X线CT全能谱图像重建改进方法[J].东南大学学报(自然科学版),2017,47(5):892-896.

10.3969/j.issn.1001-0505.2017.05.009.

10.3969/j.issn.1001-0505.2017.05.009