船舶在平整冰区行进过程的离散元分析
狄少丞,季顺迎,薛彦卓
(1. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001;2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
船舶在平整冰区行进过程的离散元分析
狄少丞1,季顺迎2,薛彦卓1
(1. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001;2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
船舶在冰区航行中,冰荷载是船舶结构设计和安全航行的重要影响因素。采用具有黏结破碎特征的离散单元法对船舶在平整冰区的航行过程进行了数值分析。在船舶破冰过程的离散元模拟中,平整冰由球形颗粒黏结而成,同时考虑了海水浮力和拖曳力对海冰单元的作用,颗粒间的黏结作用可在海冰与船体的相互作用过程中发生破碎;船体由三角形单元构造,分析了在海水浮力、推进器推力及海冰共同作用下船体的六自由度运动特性。通过船体与海冰相互作用的离散元分析,确定了船舶在破冰过程中海冰作用在船体上的冰荷载,探讨了船舶推进器推力和海冰厚度对冰荷载的影响,并与Lindqvist船体冰阻力经验公式进行了对比。
平整冰;船体;离散元方法;冰荷载;破冰过程;海冰厚度
Abstract: During the navigation of ship in ice covered regions, the ice load on ship hull is a significant factor for the structure design and safe maneuvering of ships. In this study, the discrete element method (DEM) is applied to simulate the interaction between level ice and ship hull. The level ice is constructed with bonded spherical elements under the buoyancy and drag force of current. The bonded elements can be broken in the process of the interaction between level ice and ship hull. The ship hull is constructed with triangular elements and treated as a six-degree of freedom system. With the DEM simulations of the interaction between level ice and ship hull, the global ice resistance on ship hull in the process of ice breaking can be determined. The influences of propulsive force and ice thickness on ice load are also discussed based on the simulation results. The comparison of ice load between DEM simulation results and the empirical formula proposed by Lindqvist is presented. This study can be an aid to the structure design of ship and the navigation security in ice-covered fields.
Keywords: level ice; ship hull; discrete element method; ice load; ice breaking process; ice thickness
近年来,受全球气候变暖的影响,北极海冰覆盖面积持续减少,北极航道的夏季通航也成为可能[1-2],北极东北航道和西北航道的开通对我国海上运输有着重要的战略意义[3-5]。为此,我国从2012年开始在北冰洋的考察中针对北极航道开通的可行性进行了系统的调查[4]。同时,北极海域蕴藏着丰富的油气资源,其油气储量相当于目前世界探明原油储量的13%和天然气储量的30%[6]。因此,冰区航行的安全保障和抗冰船舶的设计是当前亟待解决的工程问题。目前我国在冰区船舶航行和船体冰力研究方面还处于相对薄弱阶段。
船舶在冰区行进过程中,受海冰类型、船型和航行方式等因素的影响,使得海冰与船体的作用过程极为复杂。与船体作用时海冰通常会经历断裂、翻转、滑动清除三个阶段[7-9],同时会伴随有海冰在船艏的堆积、重叠等过程[10-11]。此外,海冰对船体冰力的大小与船舶的锚泊、直行、转向等航行方式密切相关[12-14]。在船体冰荷载研究中,通常采用现场冰荷载测量、室内模型试验、理论分析与数值分析的研究方法来揭示海冰与船体的作用机理[15-17]。而数值分析方法从揭示海冰破坏机理到船体总冰力变化规律,是研究海冰与船体相互作用的重要途径。
在船体冰荷载的数值分析中,人们发展了针对不同海冰形态特征和力学特性的数值模型[18-20]。由于海冰在与船体的相互作用过程中会呈现出由连续体向离散块体转变的破坏过程[21],且在不同尺度下海冰又呈现出离散分布特性,而在碎冰区、重叠和堆积冰区离散特性更为明显[22-24],这使得离散元方法在确定船体冰荷载方面具有明显的优势[25-27]。
为此,下文将针对海冰与船体相互作用的动力特性,建立具有黏结—破碎特征的海冰离散元方法,对海冰与船体作用时的破坏模式、船体总冰力进行数值模拟,进而分析船舶在平整冰区行进时的船舶航速及船舶破冰能力。
1 海冰与船体作用的离散元模型
1.1平整冰的离散元模型


图1 颗粒间的平行黏结模型Fig. 1 Parallel bonding model between two spherical particles
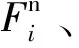

1.2船体的离散元模型
在用离散单元法研究海冰与船体的相互作用过程中,先将船体离散成三角形单元的集合,离散后的各三角形单元通过顶点相连接,通过设定海冰颗粒与三角形单元之间的接触准则即可得到海冰与船体之间的作用力。


图2 三角形单元Fig. 2 Triangular element

图3 球心在三角形面内的投影Fig. 3 Projection of center of sphere on triangle
1.2.1 接触判断
若要判定三角形单元f与某一球形颗粒p是否发生接触,首先需判定球形颗粒是否与三角形单元所在的平面有重叠。定义球形颗粒p的球心P坐标为Xp,颗粒半径为Rball,球心P在三角形单元所在平面的投影点为Q,如图3所示。
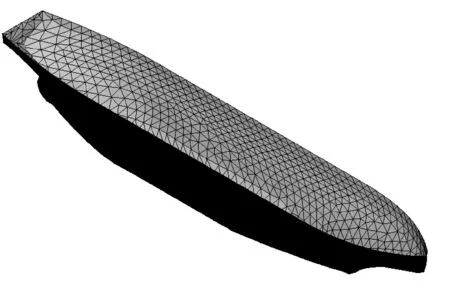
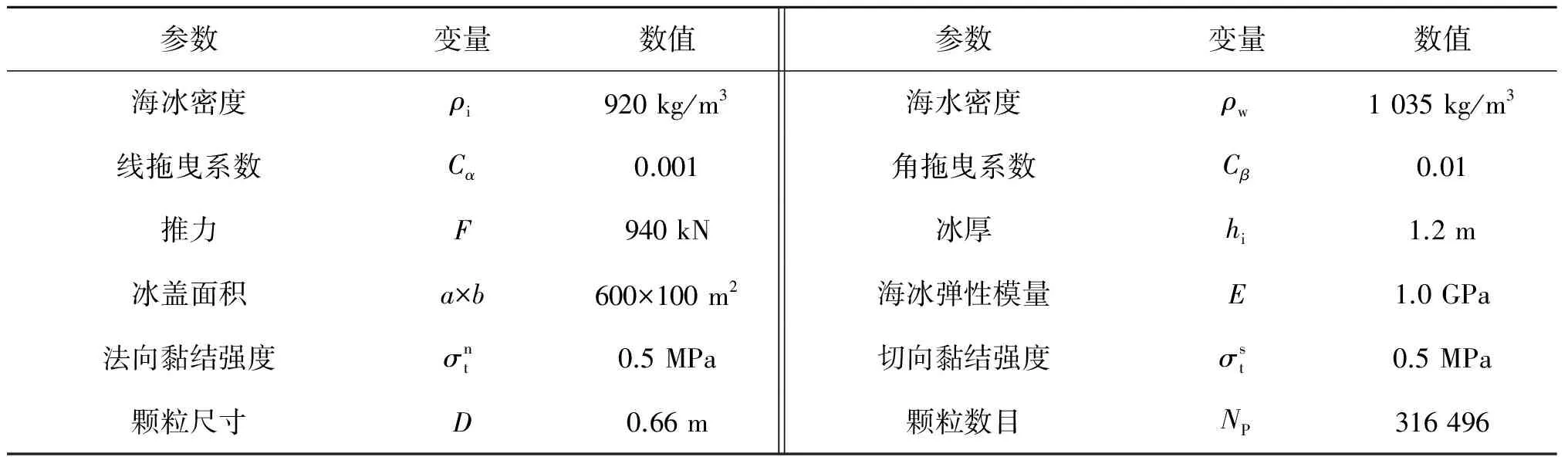
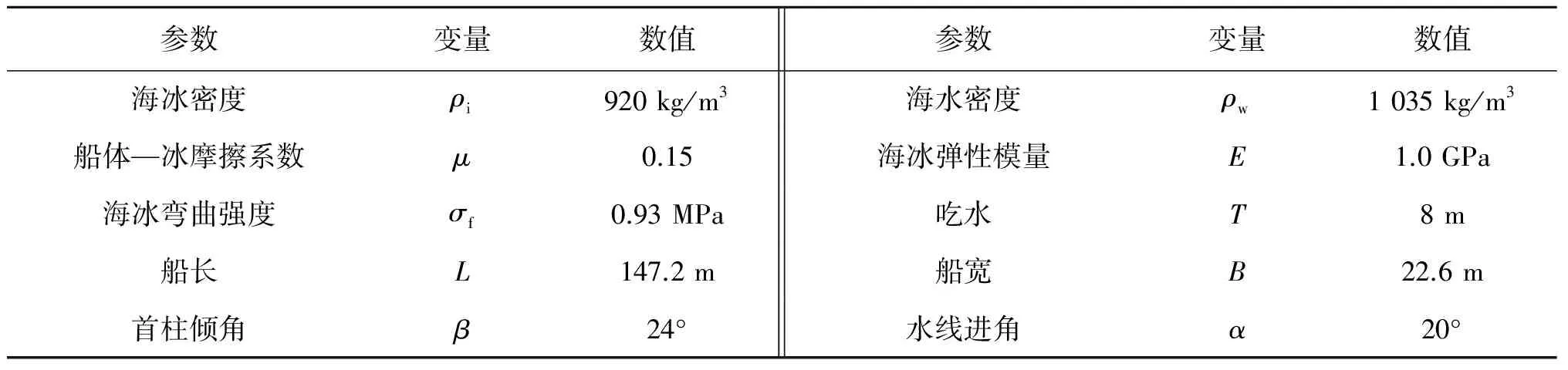
可以得到以下向量:AP、BP、CP、BA、AB、CA、AC、CB、BC、PQ,其中PQ=AP·n,如果PQ 如果球形颗粒与三角形单元所在的平面有重叠,需进一步判断球形颗粒是否与三角形单元本身接触,并判断它们的接触类型,以正确地计算颗粒与三角形单元之间的接触力。球形颗粒与三角形单元发生接触的类型有三种:球-面接触、球-边接触、球-顶点接触,以下简称为面接触、边接触和角接触。面接触是指球形颗粒球心的投影点在三角形面内;边接触是指球形颗粒与三角形单元的三条边接触;角接触是指球形颗粒与三角形单元的三个顶点接触,三种接触类型如图4所示。 图4 球形颗粒与三角形单元的接触类型Fig. 4 Contact types between spherical particle and triangular element 图5 判定投影点是否在三角形单元内部Fig. 5 Determination of the location of the projection point inside the triangle 采用重心法来确定球心的投影点是否在三角形单元内部,如图5所示,称之为第二次判定。对于平面内任意一点,都可以表示为: 如果投影点Q位于三角形ABC内部,u和v必须同时满足以下三个条件: 如果系数u和v满足式(4),则表明投影点Q在三角形单元内部,进而说明球形颗粒与三角形单元发生面接触。 如果投影点Q位于三角形边内部并且球心到投影点的距离小于颗粒半径Rball时,表明二者发生边接触,如图6所示,称之为第三次判定。 以AB边为例,点P在AB边上的投影点为Q,则 因此,当AP·BABP·BA≤0且QP≤Rball,颗粒与三角形单元发生边接触;当AP·BABP·BA>0或QP>Rball,颗粒与三角形单元不发生边接触,每个三角形单元有三条边,需做三次判定。 如果球形颗粒与三角形单元的接触关系满足第一次判定而不满足第二、第三次判定,则表明颗粒可能与三角形单元的顶点发生接触。如果颗粒球心P与顶点A、B、C之间的距离小于颗粒的半径Rball,则发生角接触,如图7所示。 图6 球形颗粒与三角形边接触Fig. 6 Contact between spherical particle and triangle edge 图7 球形颗粒与三角形顶点接触Fig. 7 Contact between spherical particle and triangle vertex 球形颗粒与三角形单元发生角接触的判断准则为:AP≤Rball,与顶点A发生角接触;BP≤Rball,与顶点B发生角接触;CP≤Rball与顶点C发生角接触。 1.2.2 接触力计算 在确定球形颗粒与三角形单元的接触类型后,即可计算出球体单元在三角形单元中的嵌入量ΔL: 式中:点PC代表球形颗粒与边界单元的接触点,分别为点Q(面接触、棱边接触);A、B、C(顶点接触)。颗粒与三角形单元接触点之间的法向量可表示为: 相对位移Δx可表示为: 其中,vp为颗粒速度,vw为三角形单元与颗粒接触点的速度。将相对位移沿接触面分解为法向分量Δxn和切向分量Δxs: 颗粒与三角形单元之间的相互作用力采用线性接触模型计算,其中法向力可表示为: 切向力的计算采用增量形式,并服从Mohr-Coulomb定律: 1.2.3 船体浮力及拖曳力计算 在本文工作中,考虑海水浮力和海流拖曳力对船体运动的影响,浮力的计算采用阿基米德原理,计算公式如下 式中:ρw为海水密度,g为重力加速度,Vsub为船体浸入水中的体积。 在离散元模型中,船体由若干三角形单元拼接而成,在计算船体浸入水中的体积时采用如下方法:取水面上任一点Pw为顶点,以水线以下三角形为底面做四面体,所有四面体体积之和即为船体浸入水中的体积,四面体的体积(如图8所示)可由下式计算: 图8 四面体单元的体积Fig. 8 Volume of tetrahedron 式中:a=v2-v1、b=v3-v1、r=p-v1,并且四面体的体心为: 因此,浸入水中船体的体积可表示为: 浸入水中部分的体心可表示为: 三角单元离散化后的船体中会有部分露出水面的三角形板,在体积计算时要特殊考虑。对于图9中所示的未完全浸入水中的三角形板,需要将露出水面的部分切除掉,只计算水下部分的体积。 图9 切除四面体露出水面的部分Fig. 9 Clipping the tetrahedron along the water line 至此求得了船体浸入水中的体积Vsub,进而由式(14)可求得船体在水中的浮力。船体在水中所受的拖曳作用由两部分组成:船体发生平动时的拖曳力Fd,以及旋转时的拖曳力矩Md。二者可表示为: 式中:Cα、Cβ分别为对应于拖曳力与拖曳力矩的拖曳系数,vw为水流速度,vs为船体平移的速度,ωs为船体转动的角速度,L为船体型长。 对比分析2014年9月—2015年8月中国大陆IMERG和CGDPA日平均降水量,结果表明:两者的空间分布比较一致,东部介于1~10 mm,西部介于0.1~5 mm,南部介于2~10 mm,北部介于0.1~5 mm,说明IMERG日平均降水量能够较好地反映中国大陆降水量西部少、东部多,南部多、北部少的特点;IMERG日平均降水量比CGDPA的空间分布连续性更好,尤其是在西部、北部等地面雨量计观测站点较少的地区(图1)。西藏东南部、新疆天山,以及青海、广西和广东南部和海南等地区,IMERG日平均降水量比CGDPA偏低。 2.1船体冰阻力的离散元模拟 以“雪龙”号极地考察船为研究对象,如图10所示,建立船体的离散元模型。由于在航行过程中只有船体外壳与海冰发生接触,因此只将船体外壳三角离散化作为“雪龙”船的离散元模型,建立的船体离散元模型如图11所示,船体离散元模型由1 430块三角形单元拼接而成。 图10 “雪龙”极地考察船Fig. 10 “Snow Dragon” polar expedition vessel 图11 船体的三角形单元离散化Fig. 11 Construction of ship hull with triangular elements 在“雪龙”船与平整冰相互作用的离散元模拟中,采用两层规则排列的球形颗粒组合来构造平整冰,平整冰排列方式如图12(a)所示。海冰的水动力特性只考虑了浮力和拖曳力,海水对海冰的浮力和拖曳力分别加到了每个颗粒上,如果颗粒全部浸入水中,浮力为整个颗粒受到的浮力;如果颗粒部分浸入水中,浮力为水面以下部分受到的浮力,拖曳力的计算与浮力类似。在模拟过程中平整冰保持固定不动,船体在推进器作用下向冰排移动。船体在运动过程中会受到海水浮力和海流拖曳力、推进器作用力及海冰的阻力,在这些力的共同作用下,船体会发生沿三个互相垂直方向上的平移和转动,规定船体行进方向为X方向,垂直于水面的方向为Z方向,X、Y、Z三个方向符合右手定则。模拟中采用的主要计算参数列于表1中。 表1 海冰与船体结构作用离散元模拟的主要计算参数Tab. 1 Major computational parameters of DEM simulation of dynamic ice load on ship hull 离散元模拟的不同时刻破冰船在平整冰区的航行状态如图12所示,船舶在恒定推力作用下驶入平整冰区时,海冰在船体的冲击下发生破碎,并在冰区内形成一条狭长的水道。船舶在驶入和驶出冰区过程中,海冰对船体在X、Y、Z三个方向上的冰阻力如图13所示。可以看出,当船体刚与平整冰接触时,船体在X、Z方向上的冰阻力随航行距离的增加而逐渐增大;随着船体的驶入,冰阻力逐渐达到最大值并稳定在一定范围内,呈现出很强的脉动特性;随着船体驶离冰区,冰阻力又开始下降,最终降为0。 由于船体在Y方向上具有对称性,使得在Y方向上冰阻力亦具有对称特性。 图12 离散元模拟的“雪龙”船在平整冰中的破冰行进过程Fig. 12 The navigation of “Snow Dragon” ship in level ice-covered regions simulated with DEM method 将图12中t= 300 s时刻的船舶破冰过程进行放大显示,放大后的破冰过程如图14所示。可以看出,船舶在行进过程中与船体接触处的海冰发生挤压破坏,而远离船体的海冰发生弯曲破坏,图14(a)中的白色折线表示海冰发生弯曲破坏所处的位置。破碎后的海冰主要集中在船体两侧(图14(b)),有部分海冰滑入船底(图14(a)),船体两侧和滑入船底的海冰均会对船体产生摩擦作用。 在推进器推力作用下船体从静止开始加速,船舶航速随时间变化曲线如图15所示。船舶从开阔水域开始加速运动,由于此时船体并未与海冰接触,因此船速逐渐增大(0 ~ 22 s);随着船体与海冰发生接触,船体冰阻力逐渐增大,此时船舶航速呈现先增大后减小的运动趋势(22 ~ 300 s);当推进器推力、海水阻力及冰阻力三者达到平衡时,船速开始保持稳定(300 ~ 500 s),本文将此时间段内的船体平均速度作为在给定推进器推力和冰厚条件下船体在平整冰区航行的速率,对应此工况下的船舶航速为1.03 m/s;最后船舶驶离冰区进入开阔水域,船速又进一步增大(500 ~ 600 s)。从图13(a)的冰阻力时程曲线可以看出,在船舶破冰过程中,冰阻力值在600 ~ 1500 kN范围内波动,但在主要破冰时间段(50~500 s)内,船舶冰阻力的平均值约为930 kN,与推力940 kN保持一致,可保证在后续时间段内船舶破冰前行。 图13 冰厚1.2 m,推力940 kN时船舶冰阻力时程曲线Fig. 13 Time history of ice resistance on ship hull with thickness of 1.2 m, propulsive force 940 kN 图14 放大显示的“雪龙”船破冰过程Fig. 14 The detail of ice breaking process simulated with DEM method 图15 冰厚1.2 m,推力940 kN时船舶行进速度时程曲线Fig. 15 Time history of navigational speed of ship with thickness of 1.2 m, propulsive force 940 kN 2.2船速、冰厚对冰阻力的影响 图17 冰厚-航速-推进力关系Fig. 17 Relationship between ice thickness, navigational speed and propulsive force 船舶在冰区航行时,航速和冰厚是影响冰阻力的重要因素。在同一推进器推力作用下,在不同冰厚的平整冰区航行时船舶的航速也将不同。本节将分析在不同推力作用下船舶在不同冰厚的平整冰区航行时的航速,平整冰的厚度分别设为0.7、0.8、0.9、1.0、1.1和1.2 m,计算中颗粒之间的黏结强度设定为同一强度,海冰在厚度方向上的颗粒层数均设为两层,采用相同的颗粒层数可保证海冰在破碎过程中具有相同的破碎特性[30]。推进器推力的设定取决于平整冰的厚度,平整冰厚度较大时设定较大的推力值,厚度较小时设定较小的推力值。采用离散元法模拟的船舶在平整冰区航行时的冰厚-航速-推力关系如图17所示,图中横坐标Vship为船舶在不同厚度的平整冰中航行时最终达到的稳定速度,纵坐标Fp为对应的推进器推力。 从图17中可以看出,“雪龙”船在较薄的平整冰区航行时只需较小的推进力即可获得较大的破冰速度;当平整冰较厚时,只有增大推进器的推力才能获得更大的破冰速度。根据“雪龙”船的航行经验,可知“雪龙”船可在1.2 m厚的冰层(含0.2 m厚的雪)中连续破冰前行,由图17可知,当推进器推力为940 kN时,可获得破冰速率为1.03 m/s(约2节);当推进器推力为1 100 kN时,可获得破冰速率为2.44 m/s(约4.8节)。 2.3与经验冰阻力公式的比较 Lindqvist冰力公式[31]是目前使用较多且较为准确的破冰船阻力计算经验公式,公式中考虑了首柱处海冰挤压破坏产生的阻力,涉及到的参数包括主尺度、船型、冰厚、摩擦以及海冰的弯曲强度。 破冰阻力Rc: 弯曲阻力Rb: 式中:hi为海冰厚度;E为杨氏模量;υ为泊松比;σf为海冰弯曲强度;B为船体型宽;ρw为海水密度。 浸没阻力Rs: 式中:ρi为海冰密度;htot为冰与雪的厚度和;T为船体吃水深度;L为船体长度。 总冰阻力Ri: 图18 冰厚-航速-冰阻力关系Fig. 18 Relationship between ice thickness, navigational speed and ice resistance 离散元模拟的“雪龙”船在平整冰区航行时船体冰阻力情况如图18所示,图19为不同海冰厚度下船舶推进力与破冰阻力之间的对应关系,其中Vship为船体在不同厚度的平整冰中航行时的速度,纵坐标Rice为船体受到的冰阻力。从图中可以看出,船体冰阻力随航速的增加呈增大趋势,但并非线性增加。在本文船体冰阻力的离散元模型中只考虑了海冰与船体的浮力与拖曳力,未考虑二者的水动力特性,这就导致了冰阻力随航速的增大趋势不明显。因此本文在对比分析中不考虑船体航速的影响,而只将不同航速下的平均冰阻力与破冰阻力、弯曲阻力、浸没阻力三者之和作比较,比较结果如图20所示。 图19 不同海冰厚度下船舶推进力与冰阻力的关系Fig. 19 Relationship between propulsive force and ice resistance under different ice thicknesses 图20 Lindqvist经验计算冰阻力与DEM模拟冰阻力的对比Fig. 20 Comparison of the ice resistance computed with Lindqvist formula and simulated with DEM method 对比分析中用到的计算参数列于表2中,表中弯曲强度值通过海冰的悬臂梁数值模型试验得到[32],离散元模型中颗粒间的黏结强度设为0.5 MPa(表1),经数值试验得到的宏观海冰弯曲强度为0.93 MPa(表2)。 表2 Lindqvist冰力经验公式中的主要计算参数Tab. 2 Major computational parameters used in Lindqvist empirical formula 从图20可以看出,在不考虑船体水动力特性的条件下,船体冰阻力随所破海冰厚度的增加而增大;离散元计算的船体冰阻力与Lindqvist经验冰力公式相比,二者较吻合,表明该离散元方法可合理模拟船舶在平整冰区的破冰过程,进而确定船舶的冰阻力。 采用离散单元法对船舶在平整冰区的行进过程进行了数值模拟,分析了船体在不同推进力、不同厚度的平整冰区内行进速度的变化规律,以及船体在行进过程中的冰阻力。以上研究表明,上文建立的离散元法可合理计算船舶在冰区的行进过程,可对海冰与船体作用过程中的破碎现象进行模拟,进而确定冰区船舶的破冰能力。在海冰破碎过程的离散元模拟中,模型细观参数的选取对模拟结果有很大的影响,例如,单元尺寸、接触模型、破坏准则等因素都会对船体的冰荷载产生影响。因此在后续工作中需进一步考虑这些因素的影响以完善海冰的离散元模型,在此基础上进一步考虑船体及碎冰的水动力特性,以更精确地模拟船舶在冰区的破冰过程。以上工作有助于揭示船体冰阻力的变化规律,为后续研究不同航行状态、不同冰况下船体冰阻力提供了有效的数值计算途径。 [1] CHIRCOP A. Climate change and the prospects of increased navigation in the Canadian Arctic[J]. Journal of Maritime Affairs, 2007, 6(2): 193-205. [2] HO J. The implications of Arctic sea ice decline on shipping[J]. Marine Policy, 2010, 34:713-715. [3] 苏洁, 徐栋, 赵进平, 等. 北极加速变暖条件下西北航道的海冰分布变化特征[J]. 极地研究, 2010, 22(2):104-124. (SU Jie, XU Dong, ZHAO Jinping, et al. Features of northwest passage sea ice’s distribution and variation under arctic rapidly warming condition[J]. Chinese Journal of Polar Research, 2010, 22(2):104-124. (in Chinese)) [4] 王洛, 赵越, 刘建民, 等. 中国船舶首航东北航道及展望[J]. 极地研究, 2014, 26(2): 276-284. (WANG Luo, ZHAO Yue, LIU Jianmin, et al. China’s first trans-arctic voyage and related expectations[J]. Chinese Journal of Polar Research, 2014, 26(2): 276-284. (in Chinese)) [5] 何剑锋, 吴荣荣, 张芳, 等. 北极航道相关海域科学考察研究进展[J]. 极地研究, 2012, 24(2): 187-196. (HE Jianfeng, WU Rongrong, ZHANG Fang, et al. The progress of expeditions and research in the seas related to the arctic passages[J]. Chinese Journal of Polar Research, 2012, 24(2): 187-196. (in Chinese)) [6] CHIERMEIER Q. The great Arctic oil race begins[J]. Nature, 2012, 482:13-14. [7] SU B, SKJETNE R, BERG T E. Numerical assessment of a double-acting offshore vessel's performance in level ice with experimental comparison[J]. Cold Regions Science and Technology, 2014, 106/107:96-109. [8] KUJALA P, ARUGHADHOSS S. Statistical analysis of ice crushing pressures on a ship's hull during hull-ice interaction[J]. Cold Regions Science and Technology, 2012, 70: 1-11. [9] SUYUTHI A, LEIRA B J, RISKA K. A generalized probabilistic model of ice load peaks on ship hulls in broken-ice fields[J]. Cold Regions Science and Technology, 2014, 97:7-20. [10] HANSEN E H, LOSET S. Modelling floating offshore units moored in broken ice: comparing simulations with ice tank tests[J]. Cold Regions Science and Technology, 1999, 29: 107-119. [11] HANSEN E H, LØSET S. Modelling floating offshore units moored in broken ice: model description[J]. Cold Regions Science and Technology, 1999, 29: 97-106. [12] IBRAHIM R A, CHALHOUB N G, FALZARANO J. Interaction of ships and ocean structures with ice loads and stochastic ocean waves[J]. Applied Mechanics Review, 2007, 60(5): 246-290. [13] KARULIN E B, KARULINA M M. Numerical and physical simulations of moored tanker behaviour[J]. Ship and Offshore Structures, 2011, 6(3): 179-184. [14] ZHOU L, RISKA K, POLACH R V B U, et al. Experiments on level ice loading on an icebreaking tanker with different ice drift angles[J]. Cold Regions Science and Technology, 2013, 85(1): 79-93. [15] GAGNON R, CUMMING D, RITCH R, et al. Overview accompaniment for papers on the barge bit impact trials [J]. Cold Regions Science and Technology, 2008, 52(1): 1-6. [16] RALPH F, MCKENNA R, GAGNON R. Iceberg characterization for the barge bit impact study[J]. Cold Regions Science and Technology, 2008, 52(1): 7-28. [17] KJERSTAD O K, METRIKIN I, LØSET S, et al. Experimental and phenomenological investigation of dynamic positioning in managed ice[J]. Cold Regions Science and Technology, 2015, 111: 67-79. [18] GAGNON R E, WANG J. Numerical simulations of a tanker collision with a bergy bit incorporating hydrodynamics, a validated ice model and damage to the vessel[J]. Cold Regions Science and Technology, 2012, 81: 26-35. [19] AKSNES V. A simplified interaction model for moored ships in level ice[J]. Cold Regions Science and Technology, 2010, 63: 29-39. [20] SU B, RISKA K, MOAN T. Numerical simulation of local ice loads in uniform and randomly varying ice conditions[J]. Cold Regions Science and Technology, 2011, 65:145-159. [21] 王钰涵, 李辉, 任慧龙, 等. 连续破冰模式下破冰船的冰力研究[J]. 海洋工程, 2013, 31(4): 68-73. (WANG Yuhan, LI Hui, REN Huilong, et al. Study of ice force about icebreaker based on continuous breaking pattern[J]. The Ocean Engineering, 2013, 31(4): 68-73. (in Chinese)) [22] DEMPSEY J P. Research trends in ice mechanics[J]. International Journal of Solids and Structures, 2000, 37: 131-153. [23] WEISS J, SCHULSON E, STERN H. Sea ice rheology from in-situ, satellite and laboratory observations: fracture and friction[J]. Earth and Planetary Science Letters, 2007, 255:1-8. [24] HIBLER W D. Sea ice fracturing on the large scale[J]. Engineering Fracture Mechanics, 2001, 68: 2013-2043 [25] LAU M, LAWRENCE K P, ROTHENBURG L. Discrete element analysis of ice loads on ships and structures[J]. Ships and Offshore Structures, 2011, 6(3): 211-221. [26] HOPKINS M A, SHEN H H. Simulation of pancake-ice dynamics in a wave field[J]. Annals of Glaciology, 2001, 33: 355-360. [27] SUN S, SHEN H H. Simulation of pancake ice load on a circular cylinder in a wave and current field[J]. Cold Regions Science and Technology, 2012, 78: 31-39. [28] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41:1329-1364. [29] JI S Y, DI S C, LONG X. DEM simulation of uniaxial compressive and flexural strength of sea ice: parametric study[J]. Journal of Engineering Mechanics, 2016: 10.1061/(ASCE)EM.1943-7889.0000996. [30] FENG Y T, OWEN D R J. Discrete element modeling of large scale particle systems-I: exact scaling laws[J]. Computational Particle Mechanics, 2014, 1(2): 159-168. [31] LINDQVIST G. A straightforward method for calculation of ice resistance of ships[C]//Proceedings of POAC, 1989:722-735. [32] SCHWARZ J, FREDERKING R, GAVRILLO V, et al. Standardized testing methods for measuring mechanical properties of ice[J]. Cold Regions Science and Technology, 1981, 4(3):245-253. Analysis of ship navigation in level ice-covered regions with discrete element method DI Shaocheng1, JI Shunying2, XUE Yanzhuo1 (1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China; 2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China) U674.21; U661.31 A 10.16483/j.issn.1005-9865.2017.03.08 1005-9865(2017)03-0059-11 2016-04-12 国家自然科学基金资助项目(51639004;51579054;41606213) 狄少丞(1986-),男,山西五寨人,讲师,从事工程海冰的数值模型研究。E-mail:dishaocheng@hrbeu.edu.cn 薛彦卓。E-mail:xueyanzhuo@hrbeu.edu.cn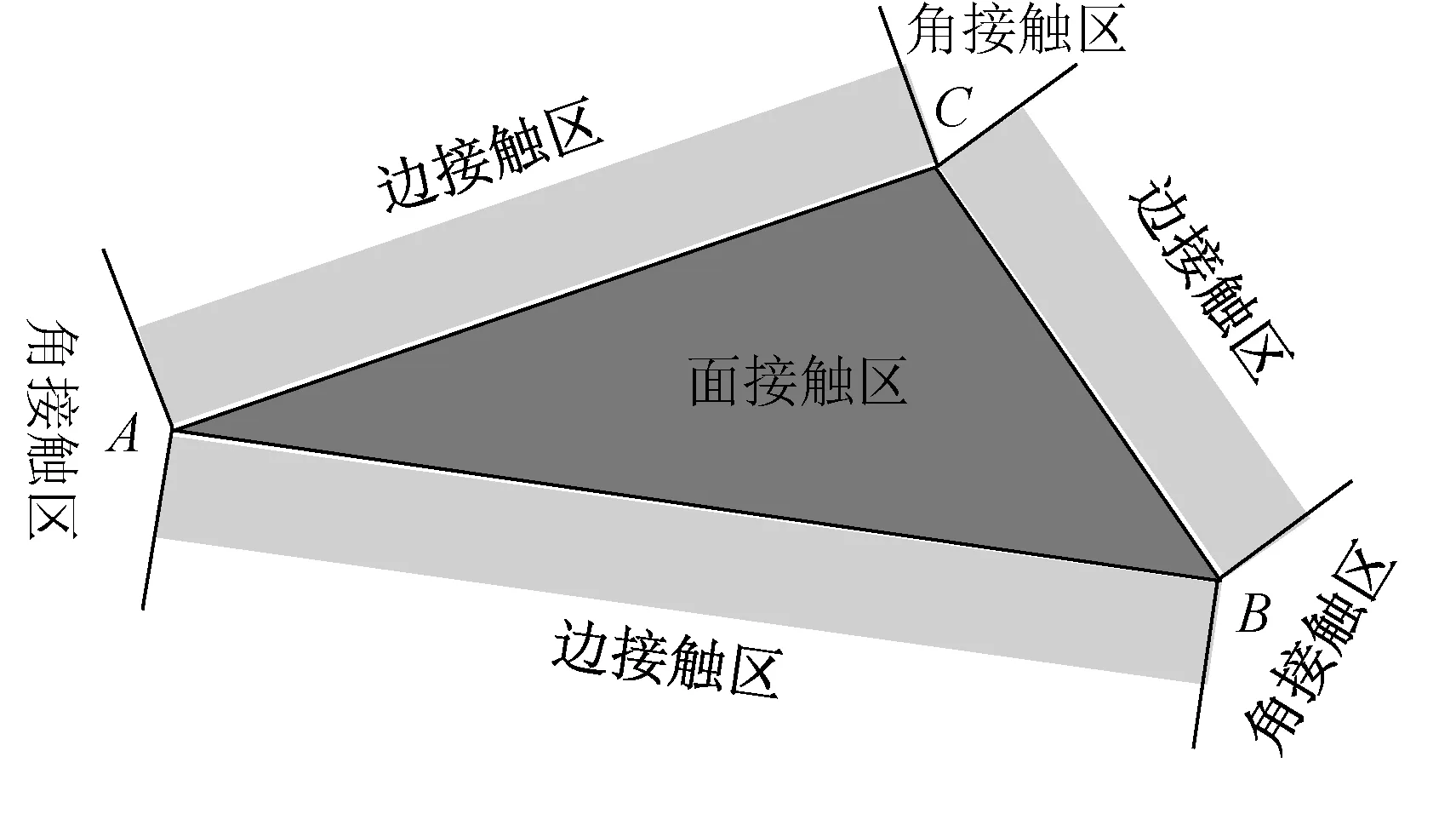







2 船舶在平整冰区直航的离散元分析











3 结 语

