海上浮式风机在支撑平台运动影响下的气动特性研究

刘格梁，胡志强，段 斐

(上海交通大学 海洋工程国家重点实验室, 高新船舶与深海开发装备协同创新中心，上海 200240)

海上浮式风机在支撑平台运动影响下的气动特性研究

刘格梁，胡志强，段 斐

(上海交通大学 海洋工程国家重点实验室, 高新船舶与深海开发装备协同创新中心，上海 200240)

浮式风机的平台作为支撑系统，其六自由度刚体运动响应决定上层风机的运动状态，也影响叶轮的环境载荷。叶轮的运动使周围流场变得复杂，叶片承受着非定常的气动载荷。研究中考虑叶片结构的运动，将基于定常流场的叶素动量理论用于局部叶素的气动分析，考虑偏航模型，充分模拟气流与叶轮的相互作用。在给定平台各个自由度运动下，计算叶轮气动参数，分析平台运动带来的影响，从入流速度方面探究引起气动载荷变化的本质原因。研究发现，叶轮气动性能和转动轴的方向有关，若平台运动改变转动轴方向，会引起气动载荷以多倍于叶轮旋转的频率发生周期变化，平台转动自由度的运动对叶轮气动性能影响显著。

海上浮式风机；气动载荷；支撑平台运动；叶素动量法；非定常分析

Abstract: This paper addresses a research on the characteristics of aerodynamic loads of Offshore Floating Wind Turbine (OFWT) associated with 6-DOF motions of the supporting platform. The performance of the wind turbine is governed by 6-DOF motion of the platform, which is deemed as the supporting base of an OFWT. Motions of the rotor complicate the surrounding flow field resulting in unsteady aerodynamic loads on the blades. A quasi-steady method is presented and the motion of the blades is combined with the Blade-Element-Momentum method to analyze the local blade load. A skewed model is introduced to simulate the interaction between wind air flow and the rotor. The calculation of aerodynamic load under prescribed single-DOF motion of the platform shows the effect of the motion on the rotor. Essential reasons for changing of aerodynamic loads are investigated from the view of inflow velocity. Results show that the aerodynamic performance of rotor is related to the orientation of rotational axis. If the orientation of the rotation axis is altered by motions of the platform, it will cause aerodynamic loads to change periodically at a frequency, which is times more than that of the rotor rotation. Thus, platform′s rotational DOFs have a significant impact on the aerodynamic behavior of the rotor.

Keywords: offshore floating wind turbine; aerodynamic loads; supporting platform′s motions; blade-element-momentum method; unsteady analysis

风机用于将空气动能转化为电能，为提供能源。一般风机的塔架结构都固定在大地或者海底，但是随着水深的增加，固定式支撑结构的设计难度以及成本都急剧增加，浮式平台支撑的浮式风机成为未来深水风机发展的必然趋势。和固定式风机不同，海上浮式风机的平台在风浪流的作用下，将发生六自由度运动，风机的气动载荷加剧了平台运动响应；同时，平台的运动导致了叶轮姿态和速度的变化，引起叶轮周围流场的非定常分布，叶轮气动载荷从而发生相应变化。叶轮不断地旋转，其气动载荷一般会随着旋转位置而变化，平台运动会影响到这种周期性变化的载荷。因此，平台运动与叶轮载荷是相互耦合的过程。

这一耦合问题为浮式风机的设计与分析带来了挑战，近年来也深受研究人员们关注。Sebastian等基于自由尾涡方法(FVM)分析了平台纵摇运动下，叶轮与下风向的尾涡相互作用，认为由平台纵摇运动引起的叶轮气动载荷的变化是不可忽视的[1]。Sebastian等认为平台运动引起了非定常的流场，对比了固定式风机与浮式风机的气动载荷，研究了不同平台形式下，对气动影响较大的平台运动自由度[2]。Jeon等采用涡格法(VLM)同样分析了纵摇运动的影响[3]。Farrugia等开展浮式平台对气动性能的试验研究，测量了叶轮的载荷和尾流状态，提出浮式风机应减小纵荡运动，以避免在叶尖速比较高状态下运行[4]。Rockel等通过风洞试验研究了平台纵摇运动对尾流的影响，浮体其他自由度的运动也可能使尾流更复杂[5]。Bayati等认识到研究浮体对气动影响的必要性，设计了在风洞试验中能为平台提供给定单/多自由度的机械装置[6]。Tran等应用CFD方法研究了周期纵摇运动对浮式风机气动的影响，并对比了其他计算模型，在大幅值纵摇运动的模拟中，CFD方法比传统气动模型计算的载荷小，且能更精确计算非定常载荷和平台随机运动的影响[7]。Sant等根据多种模型研究了平台在不同首摇角度下的叶轮性质[8]。Wu等利用CFD方法研究了平台的纵荡、纵摇和首摇对整体叶轮、单根叶片的气动载荷的影响，结合盘面和尾流的速度分布，对平台运动带来的叶轮功率、载荷变化展开分析，认为这些变化将是研究风机控制系统、结构疲劳和强度所面临的重要挑战[9]。但是，这些研究仅针对平台部分自由度运动，缺乏对六自由度运动的全面分析和对比。本文着眼于平台六自由度运动，从偏航、速度分布等方面揭示了气动载荷变化的本质原因。

本文研究海上浮式风机支撑平台运动对叶轮气动载荷的影响。先根据运动转化关系，得到叶素在平台运动影响下的运动，叠加环境风速，考虑叶轮附近相对来流的非定常性。再将受叶轮影响的空气流域分割成局部叶素影响的扇环流管，应用经典叶素动量理论分析该区域，并引入偏航模型研究来流与盘面的夹角对流场的影响。利用非定常气动模型，分析在给定平台各自由度运动情况下叶轮气动载荷的变化规律。

1 平台和叶轮的运动关系

海上浮式风机的支撑系统除了塔架，最重要的是支撑浮式平台。平台受到水动力载荷、系泊载荷，以及由塔架传递的上层结构的环境载荷和惯性载荷，其运动响应复杂。为了方便描述平台的运动，首先定义分析中所使用的坐标系，并介绍平台和叶轮运动关系。如图 1所示，定义固结于静水面的大地坐标系ox0y0z0，平行于大地坐标系且与平台固结的参考坐标系ox1y1z1，固结于平台并随之转动的随体坐标系oxyz，上层结构都在随体坐标系中表达[10-11]。平台参考坐标系原点相对于大地坐标系原点的矢径表示平台的三个平动位移，分别是沿x0方向的纵荡、沿y0方向的横荡、沿z0方向的垂荡，文中分别使用自由度编号1-3表示；平台随体坐标系相对于参考坐标系坐标轴的转动量是平台的转动位移，即绕x轴转动的横摇α、绕y轴转动的纵摇β、绕z轴转动的首摇γ，文中分别使用自由度编号4-6表示，采用卡尔丹角描述。用方向余弦阵表征坐标系之间的转化关系，方向余弦阵为：

平台的转动角速度为：

固结于平台随体系的某质点的矢径为：

质点的速度：

一般认为机舱和塔架刚性固定于平台上，安装在风机顶部的叶轮随平台运动，同时还绕转动轴旋转。叶轮上各叶素的速度表示为：

其中，rhub为轮毂中心在平台随体系中的矢径，rBE为叶素相对轮毂中心的矢径，ωR为叶轮旋转角速度。上式右端的前两项分别是平台平动和转动运动对叶素速度的贡献。

图1 平台坐标系以及风机运动的示意Fig. 1 Sketch of platform coordinate system and motions of the wind turbine

2 气动载荷计算模型

2.1经典叶素动量法

叶素动量法是计算风机气动载荷的经典方法[12]，是一维动量理论与二维翼型理论的结合。动量理论假定叶片数无穷，叶轮沿径向的流管是均匀的，流管之间相互独立互不干扰，盘面推力均匀。图 2中所示的是流管内气流速度和压强的变化关系。根据盘前盘后的运动关系，利用连续性方程和伯努利方程计算叶轮作用在流管上的力。翼型理论假设翼型展向无限长，分析流经翼型的二维流场，计算气动载荷。图 3所示，vrel为相对入流速度，α为决定载荷的攻角。假定通过上述两种方法得到的载荷相等，即可实现关键参数的求解计算。叶素动量法中最为关键的是诱导速度，表征了叶轮对气流的影响效果，通常用远前方的来流速度及轴向诱导因子a表示，用周向诱导因子a′考虑叶轮的旋转效应。根据一维和二维理论在动力上的等效关系，确定诱导速度和盘面附近空气的流动状态，计算气动载荷。

图2 一维动量理论Fig. 2 1-D momentum theorem

图3 二维翼型理论Fig. 3 2-D airfoil theory

经典叶素动量理论的推力系数表达如下：

式(6)对应图2中的动量理论，其中F为普朗特修正因子，为葛劳沃特临界诱导因子。式(7)对应图3中的翼型理论，σ为叶素实度，Cn为叶素轴向力系数。

2.2非定常气动模型

经典叶素动量法中，假定叶轮固定，来流到入流速度都是在盘面均匀定常分布的。而实际上，由于支撑系统的运动或变形会直接影响叶轮的速度、时变的风速等，任意时刻，盘面不同位置的相对来流速度是不一样的，诱导速度也呈现出随时间和空间的变化分布，很多模型都研究这类非定常气动特性[13]。本文提出使用局部叶素分析法，考虑将上述定常方法扩展至非定常气动计算，并进行局部分析。

局部叶素分析方法中，气动控制体由圆环柱状流管，变为仅受单根叶片影响的扇环流管，前述的经典叶素动量理论可以方便适用，图4给出的是三叶片风机扇环流管的示意图。

图4 受局部叶素影响的扇环流管示意Fig. 4 Sketch for a sector ring tube subjected to local blade element

通过运动学关系得到局部叶素的位置和速度vBE，根据环境条件计算该叶素位置对应的来流风速vwind，叠加得到远前方的相对远前方来流速度v，假定诱导因子a和a′，得到在叶素上的相对入流速度vrel：

此时得到的气流速度应用于翼型理论，确定局部叶素的诱导速度并计算气动载荷。

图5 叶轮偏航位置示意Fig. 5 Yawed rotor sketch

2.3偏航模型

在引入了非定常的局部叶素气动计算方法后，需要考虑局部偏航，叶轮轴向与入流速度方向不共线的位置称为偏航位置。相对远前方来流速度与叶片的局部扇形盘面非正交时，叶素处于偏航状态，引起诱导因子在空间上分布不均匀。图5所示，气流流过叶轮，尾流会倾斜，同样导致诱导速度随方位角而变化，叶片指向上风方向比叶片转动半圈后指向下风方向的诱导速度要小。偏航状态和相对远前方来流速度密切相关，考虑针对局部叶素的简单偏航修正模型[14]：

其中,γ为偏航角度，是来风速度与叶轮轴向的夹角；χ为尾流倾斜与轴向的夹角，是气流经过叶轮后与叶轮轴向的夹角；θwing为叶片当前的方位角，θ0叶片指向尾流最深处时的方位角，此时叶片所在的直径为偏航线。图5中，入流速度在xy平面内，y轴为偏航线，y轴负方向为θ0的位置。

2.4浮式风机气动载荷计算流程

平台的位移决定了风轮的位置和姿态，为了准确分析浮式风机的气动特性，在使用非定常气动模型时，计入平台运动的影响，并分析考察其中的动态规律。根据平台的运动、风机几何尺寸以及叶轮转动的速度，求出局部叶素相应的位置、速度以及轴向方向，并用于气动载荷的计算。叶轮气动载荷的计算过程如下：

1) 根据式(3)和式(4)，利用平台六自由度位移量及其导数，计算平台刚体运动速度；

2) 根据结构几何参数，计算叶素的空间位置，根据式(5)计算叶素的绝对速度；

3) 根据风参数，计算叶素的远前方来流速度，叠加叶素自身速度，由式(8)得到相对远前方来流速度；

4) 假设初始诱导因子，计算攻角，根据翼型得到动力系数，求解平衡方程，并迭代至收敛；

5) 根据叶素方向、相对远前方来流速度，计算偏航角等，利用偏航模型计算修正后的诱导因子；

6) 计算速度分布，确定该叶素的轴向、切向和转矩载荷，计算叶素对转轴的局部扭矩；

7) 根据以上步骤，计算所有叶素，得到整个叶轮的气动载荷。

本研究中，利用Fortran 2003编写了基于上述理论的计算程序，用于分析浮式风机的性能。

3 气动特性分析

以NREL 5MW上风型水平轴风机[15]为研究对象，外界环境为均匀定常风，考察在额定风速11.4 m/s、额定转速12.1 r/min情况下的气动载荷。首先研究了平台固定时风机自身的载荷特点，然后分别给定平台各自由度的位移和运动，通过载荷结果评价平台运动对气动性能的影响。

3.1平台固定时叶轮的气动特点

由于安装和安全等方面的考虑，通常会设置叶轮转动轴的倾斜角和叶片结构的锥角，文中称此类因结构布置而出现的转动角为结构角。图6中，NREL 5MW风机的叶轮设置了5°的上倾角和2.5°的锥角。

图6 NREL-5MW风机叶轮的结构角示意Fig. 6 Sketch for structural angles of NREL-5MW rotor

在计算平台运动的影响之前，首先研究了在风机的平台固定时，叶轮结构角带来的影响。结果表明，如果不存在任何结构角或者仅有叶片锥角，风机的功率和载荷等参数都是定常值，而对于设置了转动轴倾角的叶轮，其气动参数发生周期变化的。表1列出了平台固定时，风机的气动输入功率、轴向推力统计值。从表中可知，存在结构角的叶轮结构，比没有结构角对气体流动的抑制作用小，转化的风能以及受到的气动载荷也相应减小。在结构角中，转动轴倾角引起叶轮偏航，是影响载荷的主要原因。

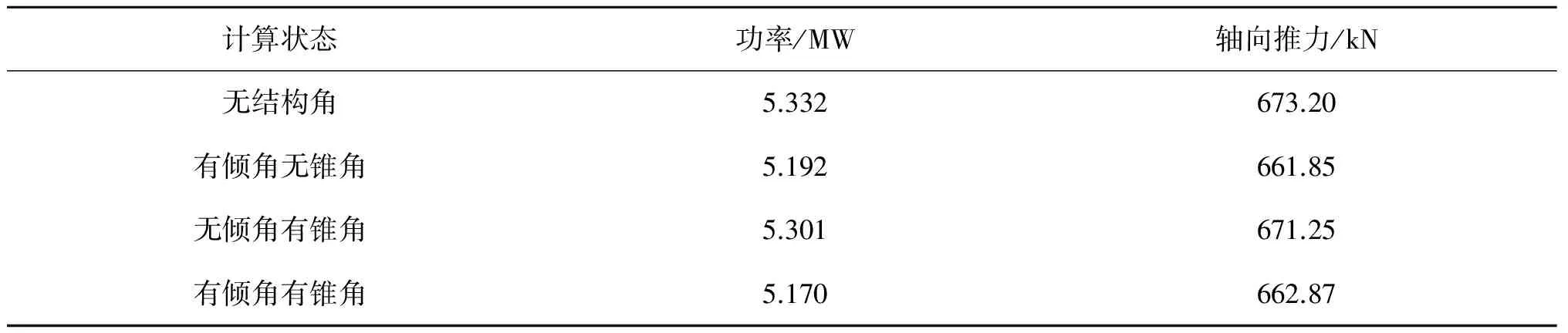
表1 结构角对风机功率和轴向推力的影响Tab. 1 Effect of structural angles on power and thrust

图7～图9给出了在平台固定时，仅有转动轴倾角的叶轮的气动功率、轴向推力和单根叶片的时历。倾角使得叶轮处于定常角偏航状态，单根叶片载荷呈1P变化关系，3叶片的叶轮整体载荷发生3P变化。从时历的结果可知，尤其是从轴向推力上，叶轮载荷关于某位置的对称性。这是由于偏航计算时，来流速度在叶片随体坐标系翼型剖面内的速度分量不变，而翼型剖面的轴向速度，即风速在叶片展向的速度分量对载荷的影响，是通过偏航修正得到的。从式(11)分析可得，叶素的诱导因子是关于偏航线对称的，故载荷关于偏航线对称。当同时存在转动轴倾角和叶片锥角时，如图8所示，此时翼型剖面内的速度在不同叶片上分量不等，仍然有3P响应，但诱导因子不再关于偏航线对称。叶片锥角的存在减少了捕获的空气能量，而叶轮转动轴的倾斜会引起偏航，因此结构角中转轴倾角决定了载荷变化的特点。考虑到结构角对气动载荷的扰动特点，在研究平台运动影响的过程中，不设置叶轮的结构角，以避免出现混淆。

图7 仅有转动轴倾角的叶轮气动载荷时历Fig. 7 Time history for aerodynamic loads of rotor with shaft tilt only

图8 同时存在倾角和锥角的叶轮气动载荷时历Fig. 8 Aerodynamic loads of rotor with shaft tilt and cone angle

图9 仅存在转动轴倾角时，单根叶片所受推力分布随时间的变化情况Fig. 9 Time-varying thrust distribution along a single blade only with shaft tilt

3.2平台各自由度对气动载荷的影响分析

为了探究平台运动对气动载荷的影响，根据表中的计算情况，为平台各自由度预设了位移和运动，对无结构角的叶轮结构进行了计算与分析，参数见表2。计算编号表示为静态定常位移或者正弦运动(S/D)-六自由度编号(1-6)-幅值编号(1-6)-频率编号(1-6)，自由度1-3为线位移，幅值单位为m，自由度4-6为角位移，幅值单位为°，定常位移末位编号为0。如D532表示计算的是无结构角叶轮在平台纵摇自由度发生幅值为8°、频率为0.15 rad/s正弦运动对应的气动情况。

表2 运动自由度的计算参数编号Tab. 2 Numbers for computing parameters of motion DOF

针对各自由度位移为定常值的情况。当平台线位移为定常值，或发生常值的横摇角位移时，叶轮的轴向方向不变，空气入流速度和叶素的速度计算都未受到平台影响，叶轮的状态与表1中平台固定无结构角的情况相同，气动载荷不变。当平台纵摇和首摇位移固定时，叶轮平面的轴向发生了变化，与远前方来流不正交，叶轮处于定常偏航状态。图10给出了S530叶轮的气动输入功率和轴向推力的时历，定常首摇或纵摇同叶轮仅存在转动轴倾角的载荷规律是一致的，都存在3P变化规律，而且关于偏航线对称的特点更为明显，都是定常偏航的结果。图11的是气动载荷随着纵摇角度的变化趋势，功率和轴向推力都随着角度增大而减小。引起叶轮偏航的纵摇和首摇既限制了气动输入功率和载荷，又引起载荷高频振荡，可见固定纵摇和首摇位移同叶轮转轴倾斜引起的偏航现象一样，对气动载荷的影响规律一致。

图10 S530(纵摇)的功率和轴向推力的时历Fig. 10 Time history for power and thrust of S530(pitch)

图11 功率和轴向推力随纵摇角的变化Fig. 11 Change of power and thrust with pitch angle

平台各自由度发生的正弦运动对气动载荷的影响不尽相同。从结果中发现，纵荡、横摇、纵摇自由度发生正弦运动时，气动载荷主要由平台运动决定，变化周期与平台运动周期相同。从图12可知，D133的气动结果，纵荡运动直接改变了相对风速，而叶轮的轴向不变，各叶素处的气动载荷受纵荡速度影响。横摇和纵摇运动影响下的结果基本一致，图13中是考虑仅有纵摇自由度运动的结果。平台发生横摇和纵摇运动，同仅有转动定常角位移带来的结果是不一样的。转动固定角度之后，平台没有速度，不影响叶轮上各处速度的分布，相对来流仍然是均匀定常风，此时定常偏航角度对气动影响明显。而平台摇动时，平台角速度引起各叶素的相对来流速度在空间上分布不均匀，且随时间不断变化，需要根据转子平面转动瞬间的角速度确定叶轮平面各点的速度，与风速叠加后，得到的相对来流随着平台的位置和速度而变化。图14中是当仅有纵摇情况下风机纵剖面的速度分布示意图。从图中可知，由于浮式风机系统纵剖面的转动瞬心一般在水线面以下，上层结构随着平台发生的转动时，叶素的速度随着高度增加而增大。从式(5)分析，由于叶轮至转动瞬心的距离和叶片长度较大，平台转动引起的叶素速度变化远大于叶轮转动的影响，盘面上叶素速度的跨度较大。因此与平台仅有纵荡运动时的结果相比，在纵摇运动下，气动载荷的振荡幅度更大。

图12 D133(纵荡)的功率、轴向推力时历Fig. 12 Time history for power and thrust of D133(surge)

图13 D533(纵摇)的功率、轴向推力时历Fig. 13 Time history for power and thrust of D533(pitch)

相对于上述三个方向的运动，平台发生横荡、垂荡和首摇运动时，叶轮的旋转会造成载荷发生周期振荡。图15和图16是平台首摇运动的结果，叶轮关于首摇轴对称，叶素的牵连速度线性分布，且叶轮的两个半面交替进入入流和尾流中，气动载荷会发生二倍于首摇频率的变化。此时叶素的速度以及偏航角度受转动的影响很明显，载荷3P响应的振荡幅值和平台转动引起的振荡幅值比较大，不利于叶轮功率稳定输出。横荡和垂荡运动结果是一致的，图17中是平台仅发生横荡的气动结果，在风速和平台运动速度叠加之后，相对来流等效为偏航角正弦变化的偏航风速，其周期为平台运动周期的一半。此时叶轮旋转引起载荷的3P振荡，但与首摇相比，振荡幅值比较小，对叶轮的影响可忽略不计。

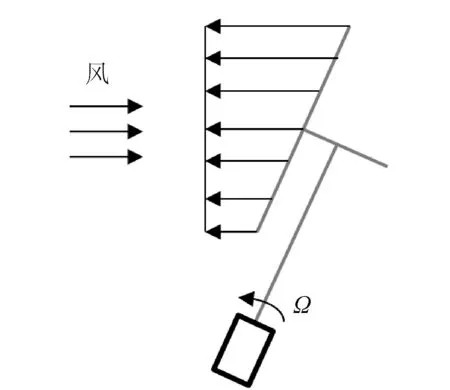
图14 纵摇运动时，叶轮纵剖面的速度分布Fig. 14 Velocity distribution in the longitudinal section of rotor when pitching

图15 D633(首摇)的的功率时历Fig. 15 Time history for power of D633(yaw)

图16 D633(首摇)的轴向推力和气动首摇力矩时历Fig. 16 Time history for thrust and aero yaw moment of D633(yaw)

图17 D233(横荡)的功率、轴向推力时历Fig. 17 Time history for power and thrust of D233(sway)

4 结 语

基于叶素动量理论，充分考虑叶轮周围流场的非定常性，计算风机的气动载荷。通过对叶轮载荷的分析，以及对平台运动与气动载荷之间对应关系的分析，探究平台六自由度运动对于气动载荷的影响程度，并得到以下结论：

1) 叶轮轴向方向是影响叶轮气动性能的主要因素，与气流完全正交的叶轮具有吸收最大风能的能力，气动载荷也最大；叶轮轴向方向变化会引起偏航，功率和载荷都减小。

2) 平台定常的纵摇或首摇位移会引起偏航，气动载荷减小，并发生3P振荡,其他自由度的定常位移影响较小。

3) 平台发生纵荡、横摇和纵摇运动时，非定常相对入流的速度主要受平台运动的影响。

4) 平台首摇运动导致气动载荷发生3P振荡，其振幅较大，影响不可忽略。

因此，为了使浮式风机获得更大的风能利用效率，应增大平台在纵摇和首摇方向上的刚度，尽可能减小因平台转动引起的偏航角，确保叶轮能够正对着来流方向。为了保证浮式风机能够安全可靠地工作，应努力限制平台纵荡和三个转动自由度的运动。

[1] SEBASTIAN T, LACKNER M A. Analysis of the induction and wake evolution of an offshore floating wind turbine[J]. Energies, 2012, 5(4): 968-1000.

[2] SEBASTIAN T, LACKNER M A. Characterization of the unsteady aerodynamics of offshore floating wind turbines [J]. Wind Energy, 2013, 16(3): 339-352.

[3] JEON M, LEE S, LEE S. Unsteady aerodynamics of offshore floating wind turbines in platform pitching motion using vortex lattice method [J]. Renewable Energy, 2014, 65: 207-212.

[4] FARRUGIA R, SANT T, MICALLEF D. Investigating the aerodynamic performance of a model offshore floating wind turbine [J]. Renewable Energy, 2014, 70: 24-30.

[5] ROCKEL S, CAMP E, SCHMIDT J, et al. Experimental study on influence of pitch motion on the wake of a floating wind turbine model [J]. Energies, 2014, 7(4): 1954-1985.

[6] BAYATI I, BELLOLI M, FERRARI D, et al. Design of a 6-DOF robotic platform for wind tunnel tests of floating wind turbines [J]. Energy Procedia, 2014, 53: 313-323.

[7] TRAN T, KIM D, SONG J. Computational fluid dynamic analysis of a floating offshore wind turbine experiencing platform pitching motion [J]. Energies, 2014, 7(8): 5011-5026.

[8] SANT T, CUSCHIERI K. Numerical modelling of the aerodynamic characteristics of a floating offshore wind turbine under yawed rotor conditions[C]//Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering. 2015: OMAE 2015-41604.

[9] WU J, DING J H, HE Y P, et al. Study on unsteady aerodynamic performance of floating offshore wind turbine by CFD method[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. 2015: ISOPE 2015-DCW-13.

[10] 刘延柱，洪嘉振，杨海兴.多刚体系统动力学[M].北京：高等教育出版社, 1989. (LIU Y Z, HONG J Z, YANG H X. Dynamics for multi-rigid-body system[M]. Beijing: Higher Education Press, 1989. (in Chinese))

[11] NEWMAN J N. Marine hydrodynamics[M]. MIT Press, 1977.

[12] HANSEN M O L. Aerodynamics of wind turbines[J]. Rotors Loads and Structure James, 2015, 5(2-3):141-167.

[13] LEISHMAN J G. Challenges in modelling the unsteady aerodynamics of wind turbines [J]. Wind Energy, 2002, 5(2-3): 85-132.

[14] BURTON T, SHARPE D, JENKINS N, et al. Wind energy handbook [M]. John Wiley & Sons, 2001.

[15] JONKMAN J M, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5 MW reference wind turbine for offshore system development[J]. National Renewable Energy Laboratory Tech. Rep., 2009: 10.2172/947422.

Research about influence of supporting platform′s motions on aerodynamics of offshore floating wind turbine

LIU Geliang, HU Zhiqiang, DUAN Fei

(State Key Laboratory of Ocean Engineering, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China)

TK83；P751

A

10.16483/j.issn.1005-9865.2017.01.005

1005-9865(2017)01-0042-09

2016-01-09

国家自然科学基金资助项目(51239007)

刘格梁(1991-)，男，江苏靖江人，硕士研究生，研究海上浮式风机。E-mail: rascalpirate@sjtu.edu.cn

胡志强(1975-)，男，博士，副教授。E-mail: zhqhu@sjtu.edu.cn