超临界二氧化碳布雷顿循环效率分析

郑开云

(上海发电设备成套设计研究院有限责任公司， 上海 200240)

研究与分析

超临界二氧化碳布雷顿循环效率分析

郑开云

(上海发电设备成套设计研究院有限责任公司， 上海 200240)

以带回热的简单超临界二氧化碳(S-CO2)布雷顿循环为研究对象，详细阐述了循环效率的分析计算方法和过程，讨论了透平入口温度和压力、压缩机入口温度和压比、透平和压缩机效率、回热器效率、压损等因素对循环效率的影响。进一步对于再压缩循环的分析表明，再压缩循环可解决“夹点”问题，从而显著提高循环效率。

超临界二氧化碳； 布雷顿循环； 效率

Abstract： Taking the simple supercritical carbon dioxide (S-CO2) Brayton cycle with recuperation as an object of study, the analysis method and process were presented for the cycle efficiency, while the effects of following factors on the cycle efficiency were analyzed, such as the inlet temperature and pressure of turbine, inlet temperature and pressure ratio of compressor, efficiency of turbine and compressor, effectiveness of regenerator, and the pressure loss, etc. A further study on recompression S-CO2Brayton cycle shows that this cycle is able to solve the problem of pinch point and, as a result, it significantly improves the cycle efficiency.

Keywords： supercritical carbon dioxide; Brayton cycle; efficiency

超临界二氧化碳(S-CO2)布雷顿循环的研究始于20世纪40年代，在20世纪60—70年代取得阶段性研究成果，之后主要由于透平机械、紧凑式热交换器制造技术不成熟而中止，直至21世纪初，S-CO2布雷顿循环的研究才再度兴起[1-4]。由于CO2化学性质稳定、密度高、无毒性、低成本，循环系统简单、结构紧凑、效率较高，S-CO2布雷顿循环被认为在第四代核反应堆(超临界水堆除外)、聚光型太阳能热发电、余热发电、地热发电等领域具有良好的应用前景[5]。

现有的研究表明，在循环效率方面，相比广泛应用的蒸汽朗肯循环，S-CO2布雷顿循环具有潜在优势，但是仍有待于对循环作深入细致的热力分析及优化。笔者主要以带回热的简单S-CO2布雷顿循环为研究对象，详细阐述了循环效率的分析计算方法和过程，讨论了透平入口温度和压力、压缩机入口温度和压比、透平和压缩机效率、回热器效率、压损等因素对循环效率的影响。由于CO2等压比热在高压侧大于低压侧，导致温差最小的位置(“夹点”)可能出现在回热器内部，无法实现理想的回热效果，所以简单S-CO2布雷顿循环的效率不高。另外笔者还对在此基础上改进的再压缩循环的效率作了进一步分析。

1 简单S-CO2布雷顿循环

1.1 循环布置

简单的S-CO2布雷顿循环(非冷凝、带回热)发电系统见图1，与此循环相对应的温熵图见图2。低温、低压工质首先进入压缩机压缩至高压，经回热器吸收透平排出工质的热量，再经热交换器从热源吸收热量达到最高温度，然后进入透平做功推动发电机工作，透平排出的工质经回热器释放部分热量，最后经预冷器冷却后进入下一个循环过程。

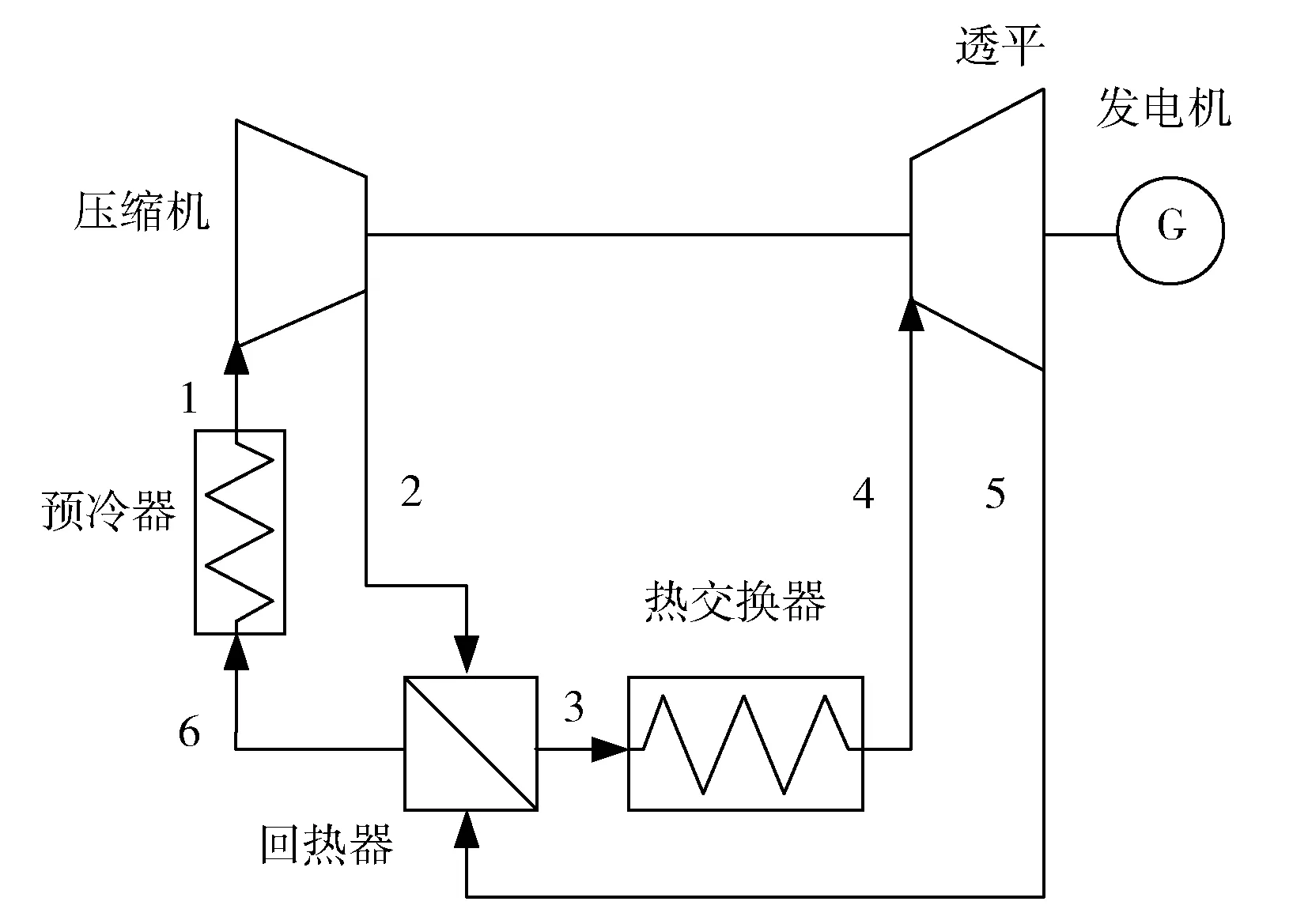
图1 简单S-CO2布雷顿循环示意图

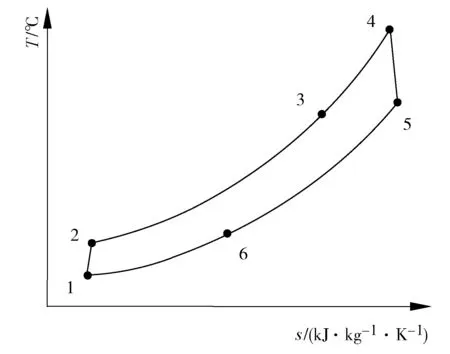
图2 简单S-CO2布雷顿循环温熵图

1.2 循环效率分析方法

基于热力学第一定律，循环的效率η可表达为：

(1)

对于简单S-CO2布雷顿循环，则有：

(2)

式中：W为机械功率；Q为热功率；h为比焓；下标in和out表示入和出，c表示压缩机，t表示透平，数字表示循环的状态点。

压缩机内的压缩过程与透平内的膨胀做功过程均视为绝热过程，等熵效率分别用ηc和ηt表示。

压缩机的压缩过程，ηc为：

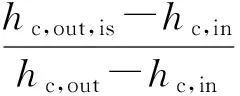
(3)

式中：is表示等熵过程。

透平的膨胀做功过程，ηt为：

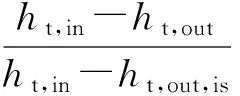
(4)

回热器的回热效率ηrec(rec表示回热器)可表达为：

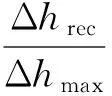
(5)

式中：Δhrec表示回热器实际换热量；hmax表示回热器理想的最大换热量。

为避免回热器内温差过小而导致传热恶化，回热器两侧工质的最小温差ΔTrec应不小于规定值。因此，回热器的热交热过程必须同时满足回热效率和最小温差的限制条件。

循环系统的压力损失主要由回热器、热交换器、预冷器等部件造成的，部件的压损率ξ表示为部件压力损失与最高压力之比。

对于循环的效率分析，事先给定的参数包括：透平入口的温度和压力、压缩机入口的温度和压比、压缩机和透平效率、回热器效率和最小温差、部件压损率。

简单S-CO2布雷顿循环最高效率的计算采用对压比ε在适当范围内进行遍历的方式，在给定范围对微小间隔的压比逐一进行分析。对于每个给定的压比，各状态点的压力值即可确定，压缩机出口(2)和透平出口(5)的状态可根据式(3)和式(4)求得，回热器中两侧工质的出口温度(3、6)采用试凑法计算。假设状态点6的温度值：

T6(n)=T2+ΔTrec+n·δt

(6)

式中：n=1，2，3，…；δt为一足够小的温度步进值(笔者取0.5 K)。由每个T6(n)求得T3(n)，然后判定是否满足回热器限制条件，其中回热效率根据式(5)计算，“夹点”温度通过计算两侧工质温度随换热量百分比的变化曲线来确定。通过循环计算直至找到满足条件的最小T6值。求得所有状态点的参数后，由式(2)计算循环效率。

循环效率分析过程采用Matlab软件编程，并调用美国国家标准与技术研究所(NIST)发布的Refprop物性数据库实现。

1.3 循环效率影响因素

影响S-CO2布雷顿循环效率的因素可分为两类：一类是来自循环系统固有的特性，对于给定的循环布置方式，即为部件的性能(如：效率)；另一类是来自循环系统运行工况，即状态点的热力学参数。

对于部件的性能对循环效率的影响，主要涉及透平和压缩机效率、回热器效率和最小温差、压损，这些参数的选取主要根据国内外调研。给定透平入口温度(550 ℃)和压力(20 MPa)、压缩机入口温度(32 ℃)，透平效率取0.9、压缩机效率取0.89、回热器效率取0.95，最小温差取10 K，忽略压损时的工况作为参照(下文中称此工况为“参考工况”)，然后，计算部件在不同性能指标下的最高效率及对应的压比，计算结果见表1。

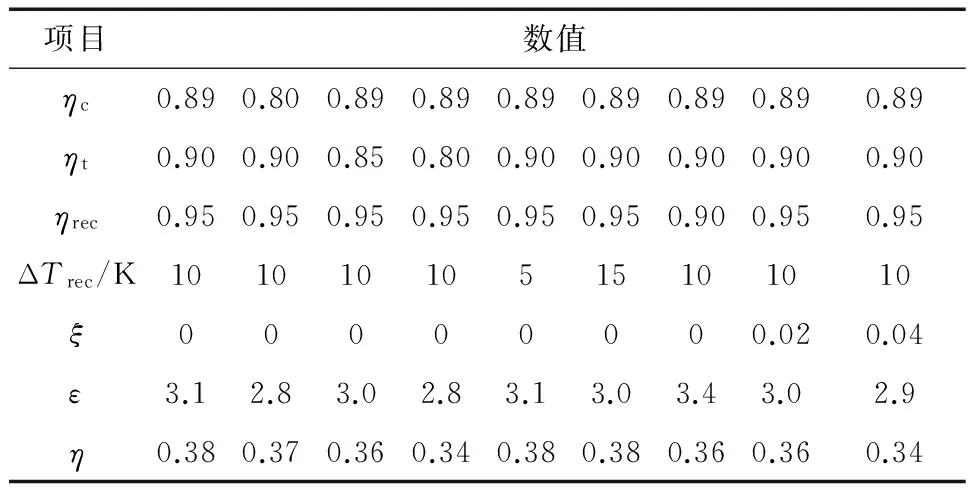
表1 简单S-CO2布雷顿循环效率与部件性能的关系

由表1可见部件性能变化带来效率变化：(1)压缩机效率下降引起的循环效率下降较小；(2)透平效率下降引起循环效率显著下降；(3)回热器效率下降引起循环效率显著下降，但最小温差几乎没有影响；(4)压损也会导致循环效率显著下降。

对于运行工况对循环效率的影响，主要研究的因素是：透平入口温度和压力、压缩机入口温度和压比。

透平入口参数对循环效率的影响分析，通过改变参考工况中透平入口温度和压力，计算循环的效率及对应的压比。计算了压比从1.2到3.7，不同的透平入口温度(350 ℃、550 ℃、750 ℃)和压力(15 MPa、20 MPa、25 MPa)下的循环效率(见图3)。在给定的透平入口温度，350 ℃时最高效率随着压力升高而显著升高，同时所对应的压比增大，但温度提高至550 ℃和750 ℃，最高效率升高不明显。在给定的透平入口压力下，最高效率随着温度升高而升高。可见，提高透平入口温度比提高压力更有优势。

压缩机入口温度对循环效率的影响分析，通过改变参考工况中压缩机入口温度，计算循环的最高效率及对应的压比(见图4)。循环效率最大值随压缩机入口温度提高而下降，与此同时效率最大值对应的压比减小。因此，对于预冷器采取空冷的情况，压缩机入口温度较高，会显著降低循环效率。

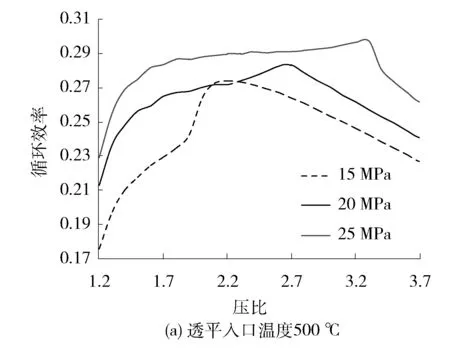
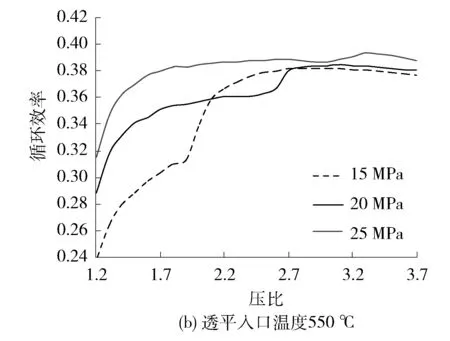
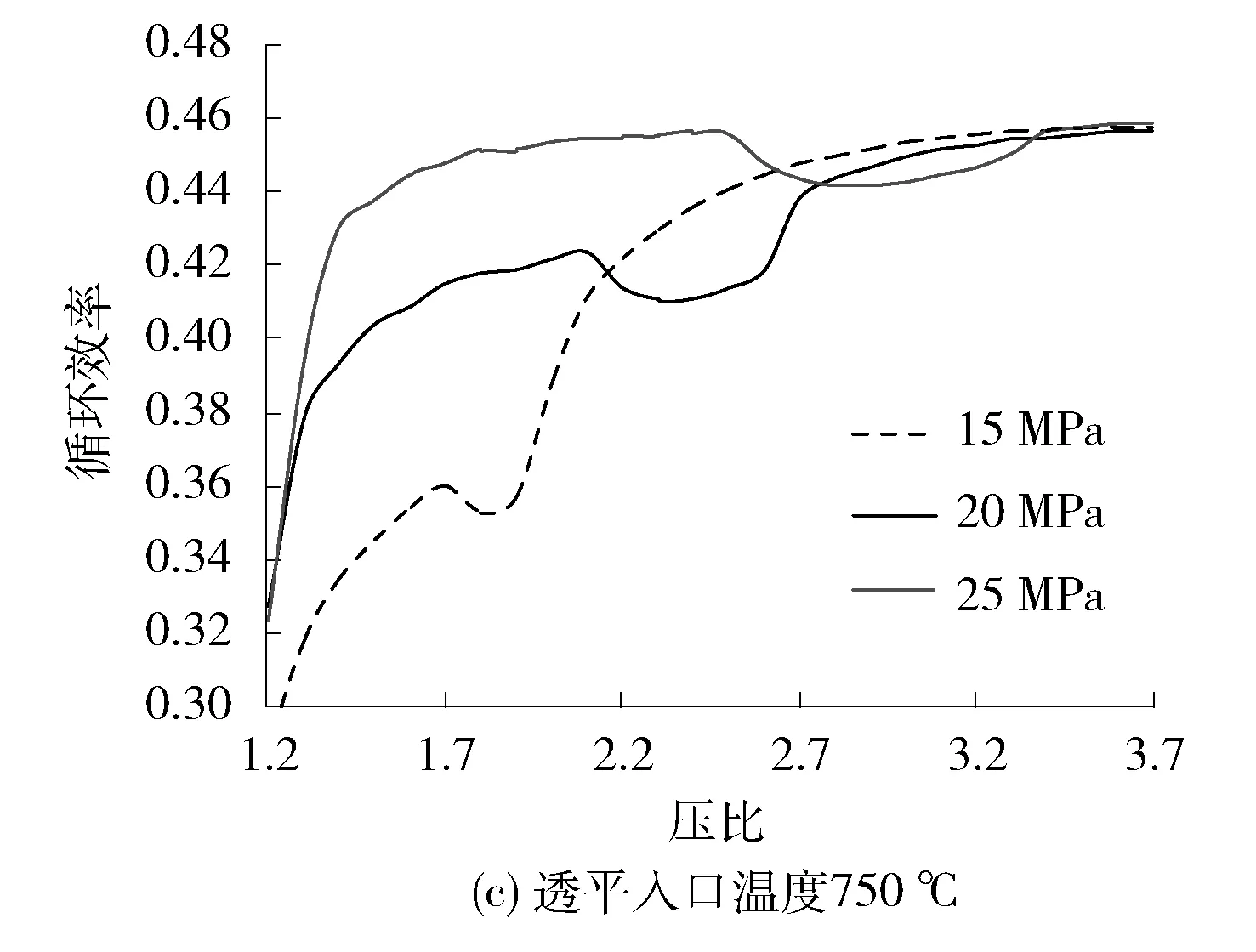
图3 在不同透平入口参数下效率与压比的关系

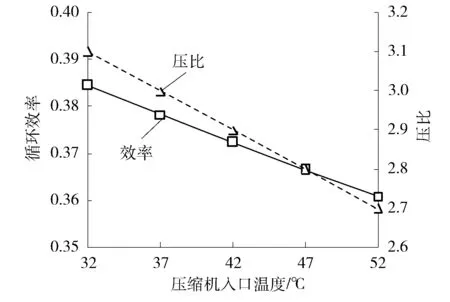
图4 最高效率及对应的压比与压缩机入口温度的关系

1.4 “夹点”问题

由以上分析结果来看，与同等参数的蒸汽朗肯循环相比，简单S-CO2布雷顿循环在效率方面的优势并不明显，这主要是由于回热器内部出现“夹点”所致，其本质是由于CO2工质在高压侧的比定压热容大于低压侧，见图5。

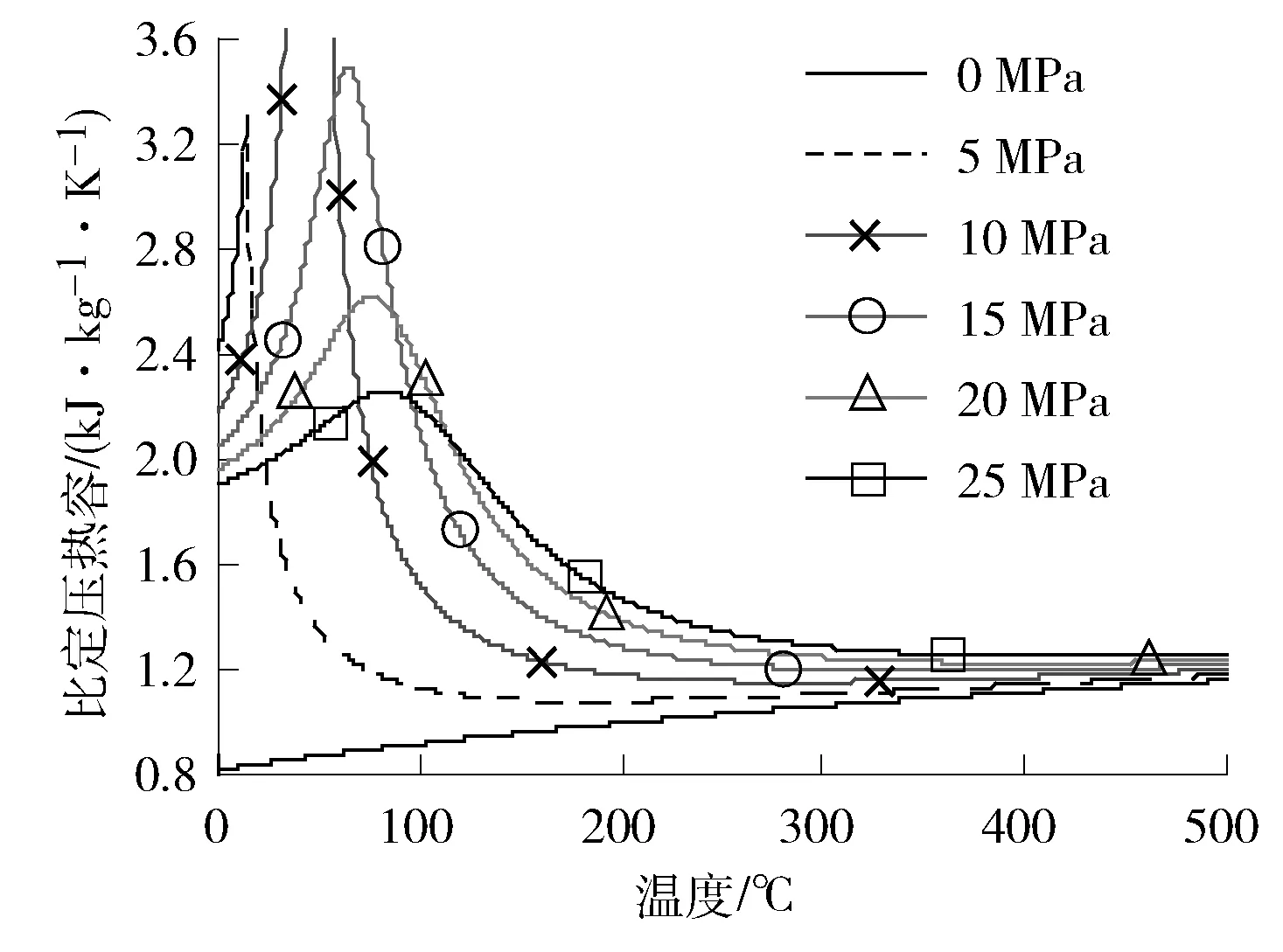
图5 CO2比定压热容与温度的关系

图6给出了在参考工况下考虑和不考虑回热器内部“夹点”时循环效率的对比。在循环计算中，不能仅考虑“夹点”位于回热器两端的情况，需要考虑回热器内部出现“夹点”的可能性。

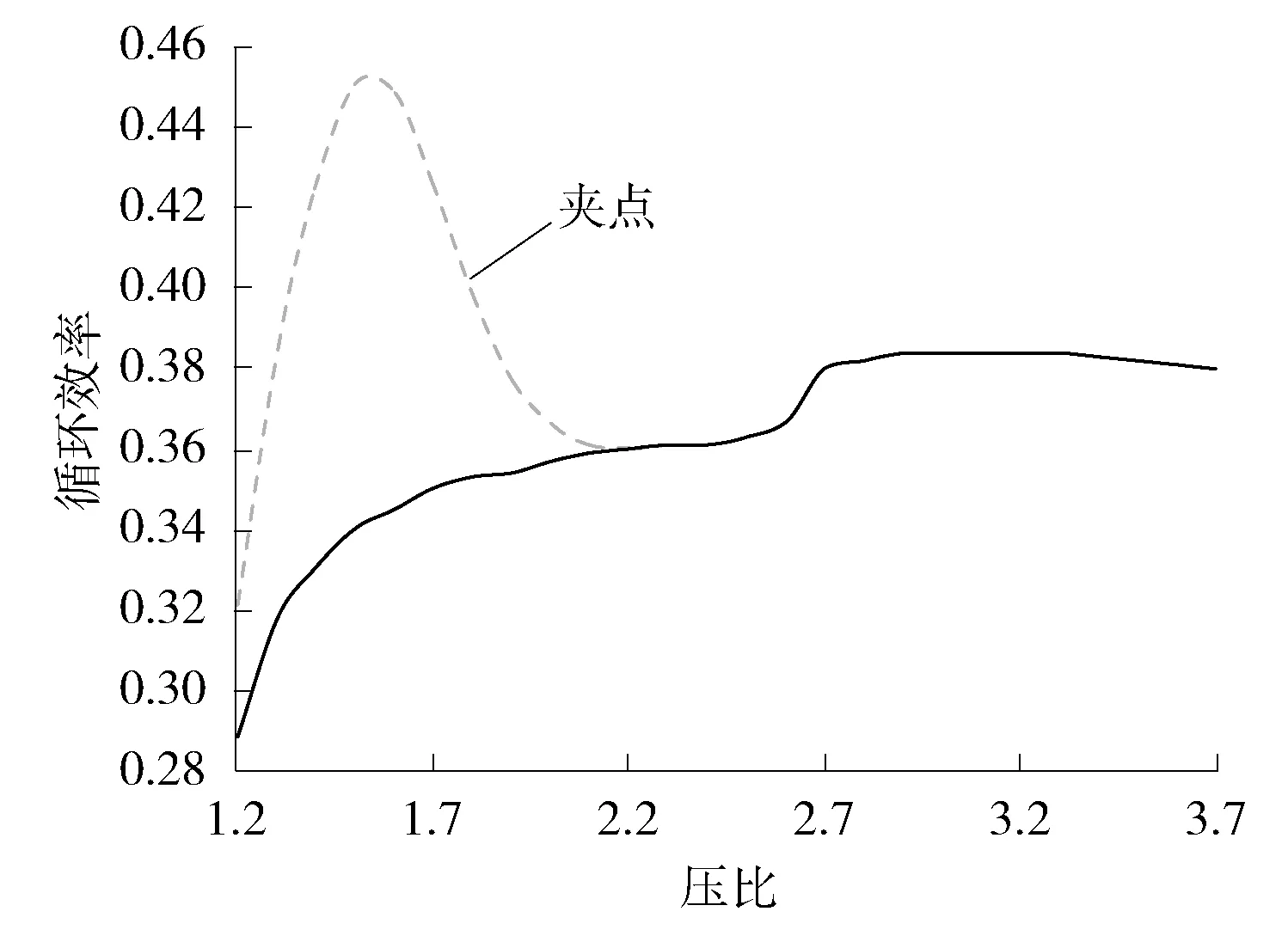
图6 考虑和不考虑回热器内部“夹点”时简单S-CO2布雷顿循环效率的对比

图7给出了压比为1.5时回热器内部两侧工质温度随换热量百分比的变化曲线。

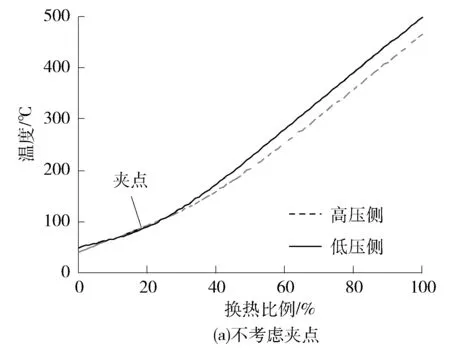
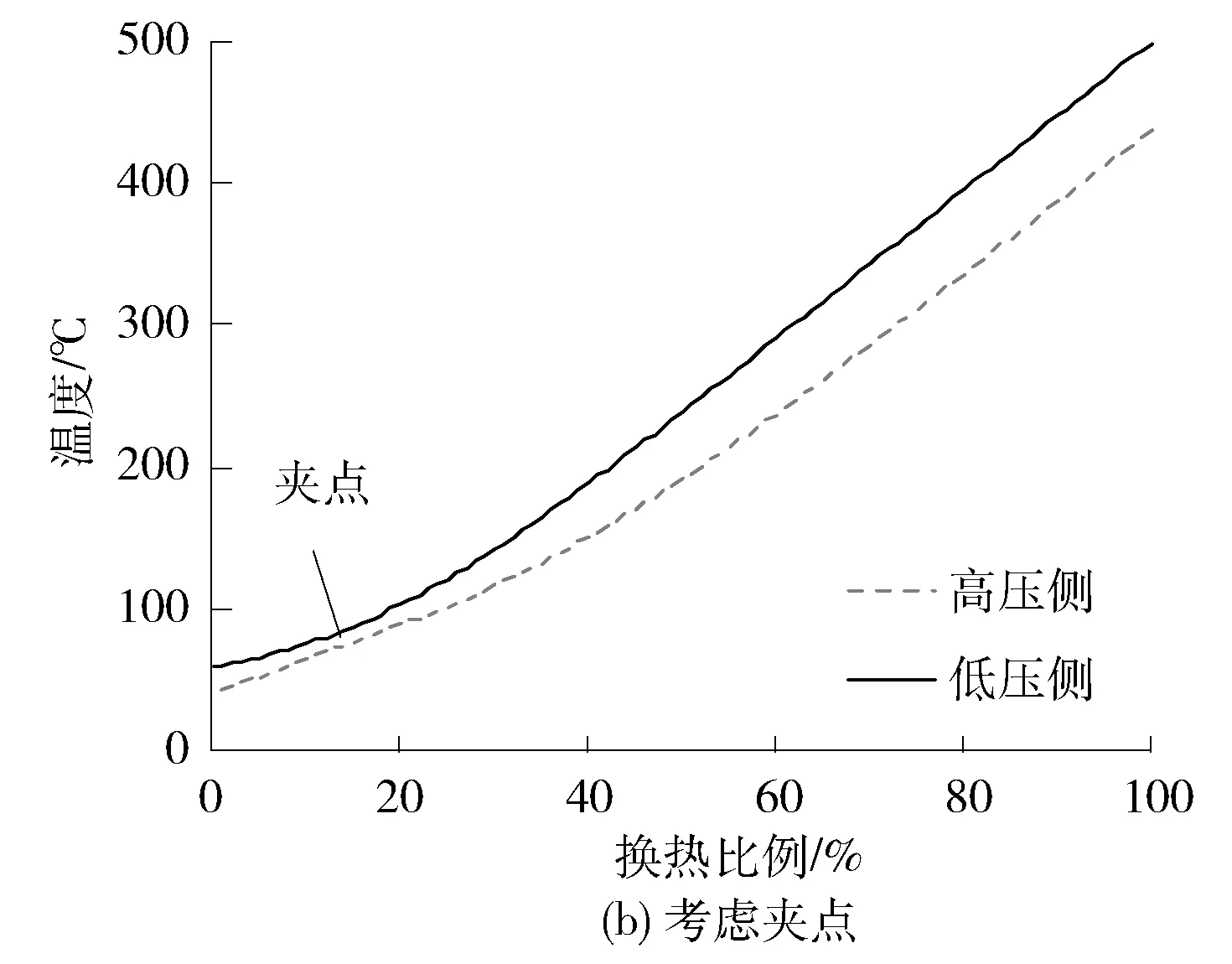
图7 回热器两侧工质温度与换热量关系曲线

由图7可见：当“夹点”位于回热器内部时，回热器两侧工质的冷热端温差显著缩小，回热器效率下降，导致循环效率降低。为解决“夹点”问题，需要改进循环的布置方式，其中最具优势的是再压缩循环[6]。

2 再压缩S-CO2布雷顿循环

2.1 与简单循环的比较

再压缩S-CO2布雷顿循环比简单循环增加一台压缩机，并且回热器分为高温回热器和低温回热器，布置见图8，与此循环相对应的温熵图见图9。与简单循环不同之处在于，再压缩循环的工质在进入预冷器前分流成两路，一路工质进入预冷器(主流)，再经主压缩机和低温回热器，然后与进入分压缩机的另一路工质汇合进入高温回热器。

图8 再压缩S-CO2布雷顿循环示意图

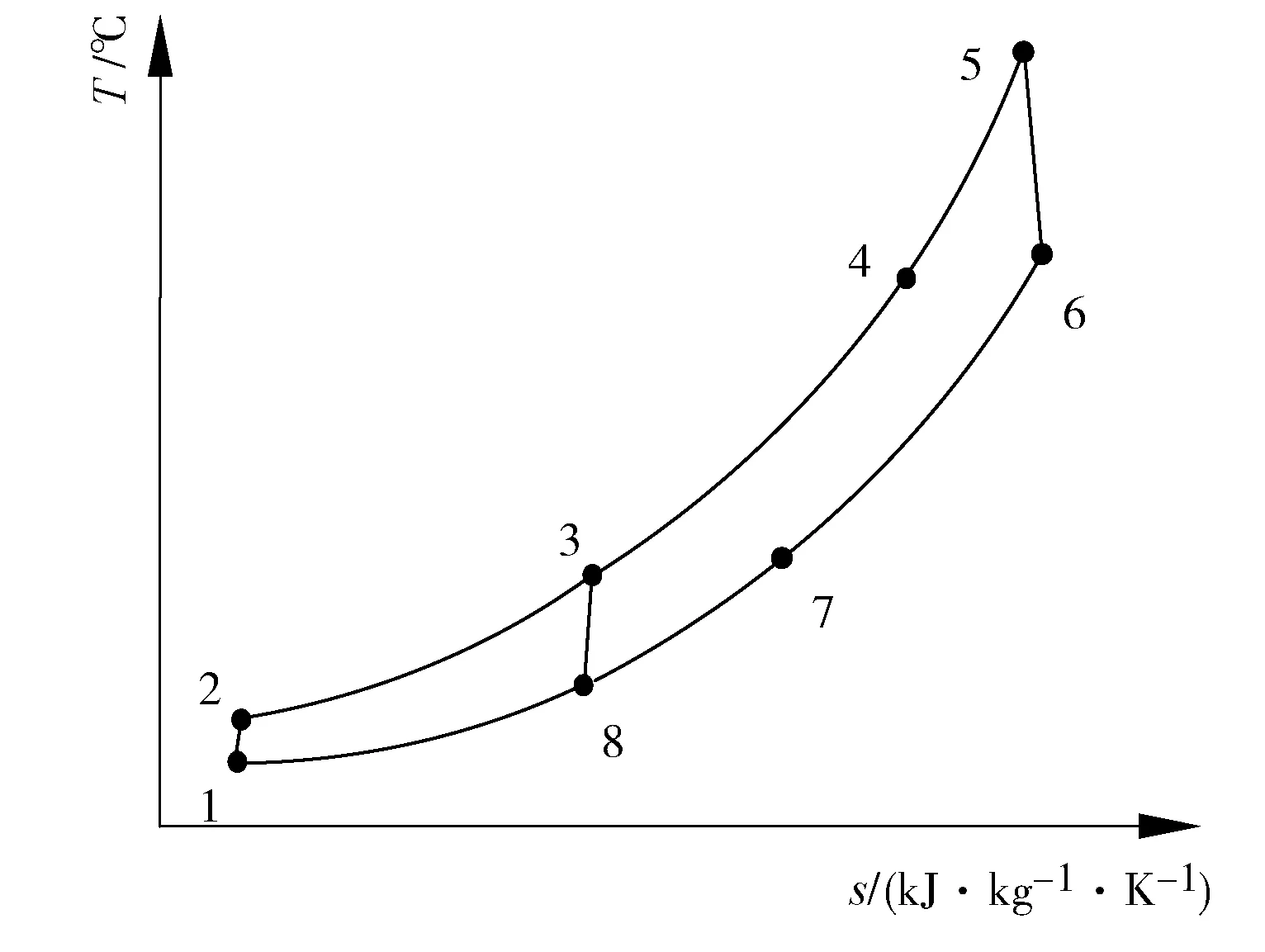
图9 再压缩S-CO2布雷顿循环温熵图

2.2 循环效率分析

再压缩S-CO2布雷顿循环最高效率的计算也采用对压比ε进行遍历的方式。回热器中两侧工质的出口温度(3、4、7、8)的计算较为复杂，对每个压比，需要求得最佳的分流配比(进入预冷器的主流份额)，比较简便的是采用循环遍历的算法，求得一系列分流配比下的状态参数和效率，选择最高效率和对应的工况。对于每个压比下的每个分流配比的具体算法，由通过在一定范围内对状态点8的温度值进行遍历计算，求得满足回热器限制条件的最佳的T8值，即对应的效率最高。因此，这一计算程序中包括对压比、分流配比、状态点8的温度的三重循环，可确保求得最高效率。

再压缩S-CO2布雷顿循环的效率分析也针对参考工况。图10给出了计算结果，可见再压缩S-CO2布雷顿循环效率(45.5%)显著高于简单循环的效率(38%)，并且可有效地避免“夹点”问题。但是应注意，再压缩S-CO2布雷顿循环的回热器换热面积增大，这会导致压损增加，削弱循环效率的优势。

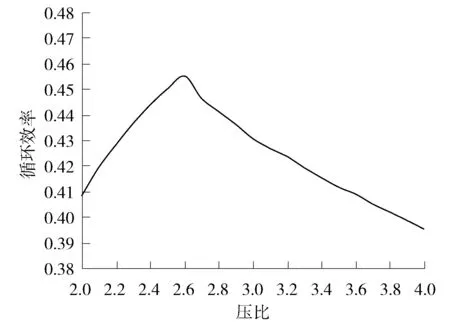
图10 再压缩S-CO2布雷顿循环效率与压比的关系

3 结语

笔者通过对S-CO2布雷顿循环效率的分析和讨论，主要结论如下：

(1) 简单S-CO2布雷顿循环效率受到部件性能和运行工况两方面的影响，提高部件性能、提高透平入口参数、降低压缩机入口温度等措施都在不同程度上有利于循环效率的提高。

(2) 由于“夹点”问题，简单S-CO2布雷顿循环在效率方面无显著优势，需要改进循环的布置方式，以提高效率。

(3) 再压缩S-CO2布雷顿循环效率较高，并可避免“夹点”问题。

[1] FEHER E G. The supercritical thermodynamic power cycle[J]. Energy Conversion, 1968, 8(2): 85-90.

[2] ANGELINO G. Carbon dioxide condensation cycles for power production[J]. Journal of Engineering for Power, 1968, 90(3): 287-295.

[3] COMBS O V. An investigation of the supercritical CO2cycle (Feher cycle) for shipboard application[D]. Massachusetts: Massachusetts Institute of Technology, 1977.

[4] DOSTAL V, DRISCOLL M J, HEJZLAR P. A supercritical carbon dioxide cycle for next generation nuclear reactors[R]. Massachusetts: Massachusetts Institute of Technology, 2004.

[5] AHN Y, BAE S J, KIM M, et al. Review of supercritical CO2power cycle technology and current status of research and development[J]. Nuclear Engineering and Technology, 2015, 47(6): 647-661.

EfficiencyAnalysisforSupercriticalCarbonDioxideBraytonCycles

Zheng Kaiyun

(Shanghai Power Equipment Research Institute Co., Ltd., Shanghai 200240, China)

2016-11-30；

2017-12-11

郑开云(1980—)，男，高级工程师，主要从事动力循环技术研究。

E-mail: zhengkaiyun@speri.com.cn

TK121

A

1671-086X(2017)05-0305-05