数学知识在高中物理解题中运用的几点思考

杜云涛

摘 要：任何学科的知识都是可以互相关联的，尤其是理科中数学和物理的结合上，在许多的物理习题中都有所体现。通过了解代数知识和几何知识在物理解题中的运用，我们可以对数学知识在物理解题中的运用技巧进行了全方位的探究。

关键词：数学知识；高中物理；解题技巧；应用

中图分类号：G63 文献标识码：A 文章编号：1673-9132（2017）30-0110-02

DOI：10.16657/j.cnki.issn1673-9132.2017.30.070

在知识的海洋里，我认为，许多知识都是融会贯通的，虽然它们在实际应用和学习中都各有侧重，但是仔细推敲一下，仍有很多相关联的地方，尤其是理科中数学和物理的结合上，在许多的物理习题中都有所体现，在解决物理题目的时候，运用一定的数学知识解题是很有必要的。

一、 数学知识在物理解题中运用的方向

（一） 代数知识在物理解题中的运用

第一，很多的物理公式实际上都是像方程式一样，需要像数学公式那样举一反三，通过方程中的已知项推导出未知项；第二，物理习题中广泛应用了代数中的抛物线，如果能和数学中的抛物线方程进行对比联想，也很容易找到解题的思路；第三，代数中未知项x在物理解题中的应用广泛，可以把物理中需要求值的数字设为x，根据公式等来推导出物理习题的答案。

例如有这样一道物理题：做自由落体运动的物体在最初一秒内下落的距离等于整个下落高度的9/25，求他下落的高度。如果在最后一秒内下落的距离等于整个下落高度的9/25，求他下落的高度。

这道题的答案是：

1. 第一秒下落的高度为h=1/2gt^2，t=1s，h=5m，下落距离为整个高度的9/25，总高度H=5*25/9=125/9；2.从题设中的比例关系数9/25，相等时间内通过的位移比为1：3：5：7：9，而且1+3+5+7+9=25，最后一秒的位移恰好为总位移的9/25，一共五段位移，下落了5s，H=0.5gt^2=0.5*10*5^2m=125m

从答案解析中不难看出，整道题都是对一些公式的计算和套用，而且运用了很多数学的解题思路和方法，例如数学中的位移比问题和很多的运算过程等等，由此可见数学代数知识在物理解题中运用的重要性。

（一） 几何知识在物理解题中的运用

物理习题中，很多都可以通过画图的方式解决问题，因为物理题目大多比较抽象，需要用到联想把题目中的要求在心里还原成现实。但是，只有还原是远远不够的，有时候，还需要把还原的场景进行抽象的概括，通过分析概括后的图形找出解题的思路，而最后概括出的抽象圖形，几乎都可以通过运用几何知识进行解决，例如这样一道物理题：

宇宙中距离较近的两个星球组成双星，它们在相互之间的万有引力作用下，绕二者连线上某点做周期相同的匀速率圆周运动，现测得这两个星球球心之间的距离为R，其运动周期为T，求这两个星球的总质量。

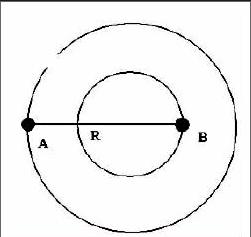
这道题表面上看起来十分抽象，因为天体是巨大的，但是可以借助数学中的几何知识把这两个星球变成两个圆形或者球体来看，进而画出图形：

这样便很快有了解题思路：如图所示，两个星球组成的双星A、B，质量分别为MA和MB

由万有引力定律可知，A、B星球之间的引力F为：

（1）F=G×MA×MB/R2

其次，由于两星球分别做圆周运动，令其半径分别为rA、rB可列方程：

对于A星球：

（2）F=MA×（2π/T）2×rA

对于B星球：

（3）F=MB×（2π/T）2×rB

另外，有

（4）R=rA+rB

综上方程，可解出两星球总质量（MA+MB），

（MA+MB）=（2π/T）2R3/G

二、 数学知识在物理解题中的运用技巧

（一）用数学思维解题

数学中我们常会用到逻辑思维、抽象概括思维和想象力，那么在解决物理题目的时候就可以把这些思维一一的应用一遍。例如，通过把某个未知的数值设定为x，把一个具体的图形变成一个抽象的图形等，可以把物理题中所说的天体行星设想成圆形或者球体，把承载拉力的弹簧想象成为直线等等，通过抽象思维把复杂的物理图形变成简单的数学图形等。通过巧妙的简化，把数学思维应用到物理的解题中去。

（二）用数学的解题方法解答物理问题

常用的数学解题方法主要有：配方法、换元法、待定系数法、数学归纳法、数形结合法、分类讨论法等等，这些常用的数学方法在解题中，很多都可以应用到物理中去，例如待定系数法，可以在物理习题中，把需要求的数设成x，把物理题还原成简单的x方程问题来解答；再如数形结合法也可以应用到物理解题中去，例如先把物理中需要画图的地方用图形表示出来，然后像解决数学题那样在图片上标示出相应的数字，然后根据数形结合来找出解题的思路。

（三） 用数学的公式解决物理问题

在物理习题中，同样可以利用数学的相关公式来解决问题，例如在力学上，很多力的相互作用图都可以构成三角形，然后根据勾股定理等几何原理，就可以把复杂的物理力学题转化为简单的几何题来做。此外，很多数学公式的推导对于物理解题来说都很有借鉴意义，尤其是公式之间的互相转换等等，通过一些数学公式的推导过程为物理解题提供思路。

（四） 用数学的运算思维解决物理问题

很多物理问题都需要一定的运算，这些运算虽然不像数学运算那般繁琐，但是在做题的时候也相对浪费了不少时间。为了尽可能地提高做题效率，我认为可以运用数学中的运算思维来应用到物理的运算中去。例如，很多繁琐的数学运算，如果仔细推敲的话，都有一些比较简单的算法，我们完全可以把数学运算的巧妙方法运用在物理解题中，让物理题目的解题过程变得更加简洁、快速。

综上，是我对数学知识在高中物理解题中运用的几点思考，其实，数学和物理同属于理科，两者可以说是相辅相成，不可偏废的，尤其是在遇到这两门学科产生关联的时候，完全可以借用彼此的思维独特之处来换个思路和方法解题，这样既可以提高解题效率，同时还可以在解题中互相促进两个学科知识的掌握，对学习数学和物理都大有裨益。

参考文献：

[1] 杜文权.初中物理解题的数学思维技巧[J].理科考试研究，2016（12）：71.

[2] 李新红.初中物理解题“数学化”成因分析及矫正策略[J].中学生数理化（教与学），2017（3）.endprint