火星车三折平展坡道转移方案及转移姿态分析

刘卫，钱成，马超，姜生元

（1.北京空间飞行器总体设计部，北京 100090；2.哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 150080）

火星车三折平展坡道转移方案及转移姿态分析

刘卫1，钱成2，马超2，姜生元2

（1.北京空间飞行器总体设计部，北京 100090；2.哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 150080）

以火星车从着陆平台安全转移至火星表面为研究目标，提出一种三折平展坡道转移方案。火星车坡道式转移方案难点在于，着陆点地形地貌不确定和着陆器自身姿态的不确定将导致火星车转移姿态不确定从而增大转移风险。为保证火星车坡道式转移安全性，开展火星车坡道式转移姿态分析，获得满足火星车安全转移要求的最小坡道长度并评价出极限转移姿态。为使三折坡道展开总长度尽可能靠近最小坡道长度需求，进行了三折坡道长度优化分析，获得在着陆器构型约束下三折坡道长度最大值，可为我国火星车转移工程实施提供借鉴。

火星着陆巡视探测；坡道；转移姿态分析；优化

0 引 言

随着我国航天科学技术的不断发展和进步，特别是“玉兔号”成功登陆月球并进行着陆巡视探测，我国势必将着陆巡视探测目标瞄准更为遥远的深空。2016年1月11日，中国首次火星探测任务正式立项，争取在2020年这个发射窗口一步实现对火星的环绕探测和着陆巡视探测[1-2]。

迄今为止，人类成功进行的火星着陆巡视探测共有4次。美国“火星探路者”（MPF）于1996年12月发射，此探测器采用气囊缓冲装置成功着陆火星，着陆平台收拢时是四面体结构，展开后由1块基板和3块侧板组成，火星车安放在其中一块侧板上，初始距星表高度约0.6 m，火星车利用展开后的侧板转移至火星表面。2003年，美国向火星分别投送了两台相同的“火星探测车”（MER）——“勇气号”“机遇号”，与MPF着陆平台相似，MER着陆平台也是由1块基板和3块侧板组成，火星车放置在基板上，初始距星表高度约0.5 m，侧板之间连接有由芳香族聚酯纤维材料制成的布幅，侧板展开后布幅在3个均等方向形成平整的通道，火星车选择任意1个通道进行转移。2012年8月6日，“火星科学实验室”（Mars Science Laboratory，MSL）携带的“好奇号”火星车采用空中悬吊机在火星表面成功着陆，实现了使质量为900 kg的有效载荷在火星着陆[3-6]。

通过对国外已经成功应用的火星车着陆转移技术分析可知，火星车一般不能直接降落在火星表面，需通过带有缓冲装置的着陆平台进行搭载，待着陆平台软着陆后，火星车通过转移机构安全转移至火星表面[7-11]。针对我国基于着陆平台的火星车转移任务，本文提出了一种三折平展坡道转移方案。由于火星车坡道式转移姿态的不确定，为保证转移安全性，进行火星车坡道式转移姿态分析，获得满足火星车安全转移要求的最小坡道长度并评价出极限转移姿态。为了使三折坡道展开后总长度尽可能靠近火星车安全转移的最小坡道长度，开展三折坡道长度优化分析，获得在着陆器构型约束下三折坡道长度最大值。

1 三折平展坡道转移方案

根据着陆器构型条件及火星车悬架构型，提出火星车三折平展坡道转移方案，其工作原理如图 1所示：①坡道在发射段、地-火轨道转移段、着陆段处于折叠压紧状态，待着陆器安全着陆在火星表面后，根据着陆区域地形地貌，确定火星车转移方向，假设坡道确定沿+Z方向展开，则-Z方向摆转铰链火工品解锁，为坡道展开做好准备；②第一段坡道在展开铰链扭簧驱动下展开，由于型约束压紧座的约束作用，待第一段坡道展开到与第二段成一条直线时，第二段坡道才能进行展开，从而实现了相邻两段坡道顺次展开；③在展开铰链扭簧驱动下，第二段坡道与第三段坡道展开成一条直线；④在摆转铰链作用下，第三段坡道展开到沿+Z方向，并发生摆转使坡道末端接触火星表面，形成供火星车转移的通道，为火星车转移做好准备。

图1 三折平展坡道工作原理图Fig.1 Working principle diagram of tri-folded and deployed type ramp

三折平展坡道系统组成如图 2所示。系统由两套对称布置在着陆平台顶面的坡道组成，待着陆器软着陆并确定展开方向后，坡道一端的火工压紧组件解锁，3段坡道顺次展开并发生摆转形成供火星车转移的坡道。系统各组件功能如下：①火工压紧组件，使坡道处于压紧状态，决定坡道展开方向；②型约束压紧座，使坡道处于压紧状态，为坡道顺次展开提供运动副；③展开铰链组件，提供展开驱动扭矩；④摆转铰链组件，坡道展开到位后，使坡道发生摆转接触并适应火星表面局部地貌；⑤平台护栏组件，确保火星车从着陆平台进入坡道；⑥坡道组件，承受火星车载荷，是火星车从着陆平台转移至火星表面的通道。

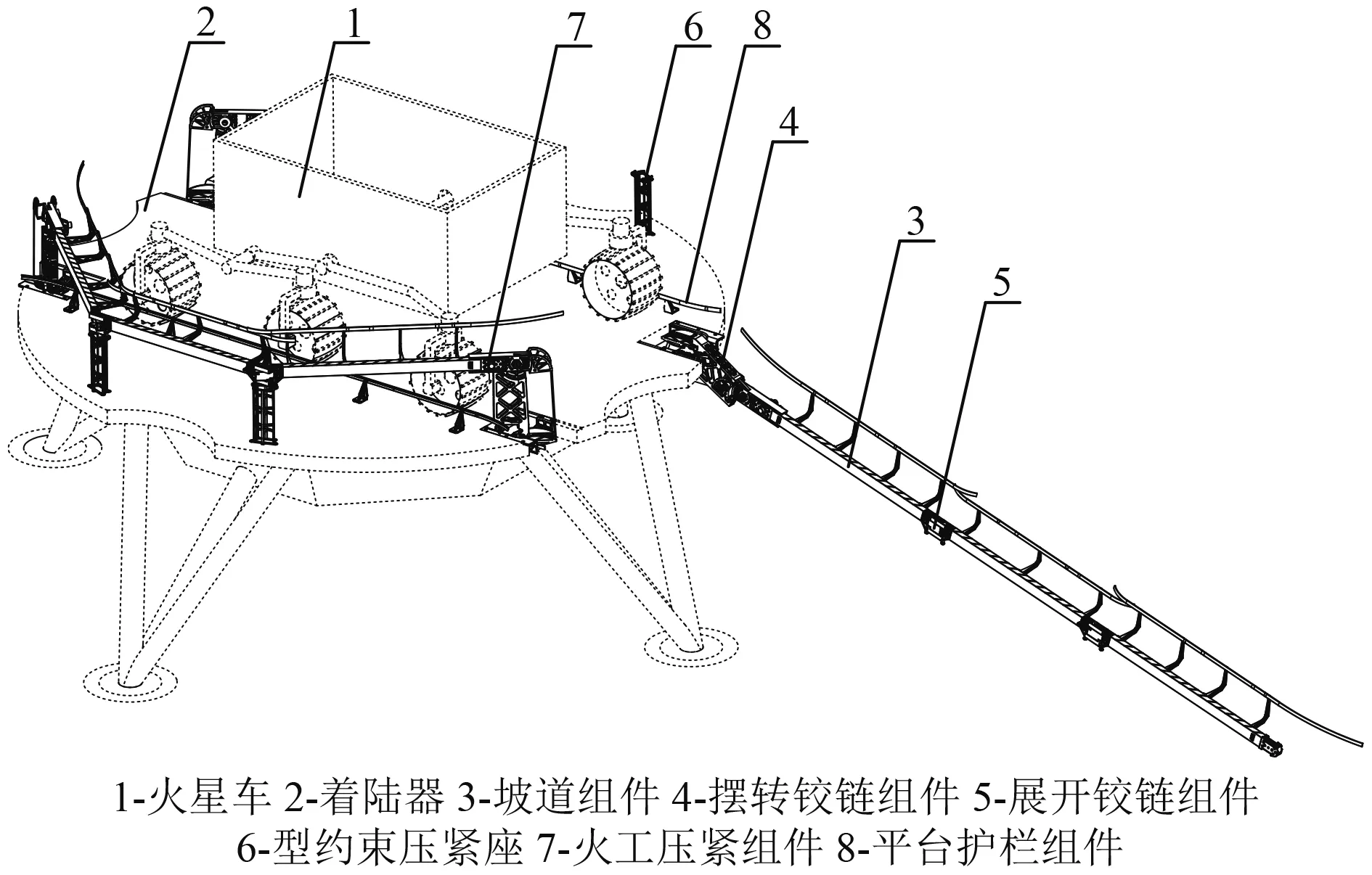
图2 三折平展坡道系统组成Fig.2 System composition of tri-folded and deployed type ramp

2 火星车坡道式转移姿态分析

2.1 坐标系定义

针对提出的火星车坡道式转移方案，本节开展火星车坡道式转移姿态分析，以获得满足火星车安全转移要求的最小坡道长度并评价出极限转移姿态。为保证火星车安全转移，转移坡度角θ和坡道异面角γ应满足一定条件。转移姿态的不确定性包括：①着陆平台预期的着陆平面可能是水平面或是与水平面有一定夹角的坡面且最大坡度不超过8°；②三折坡道末端可能落在火星表面的岩石或凹坑上，且岩石或凹坑的最大包络尺寸小于200 mm；③着陆平台在火星表面着陆后，4组着陆腿会产生不等量的压缩，从而导致着陆平台与着陆平面产生一定的俯仰或侧倾角度，其最大值不超过6°。综合考虑以上3方面因素，火星车坡道式转移姿态有无限多种可能，本文定义典型侧倾和典型俯仰转移姿态，进行转移姿态分析数学模型的建立，定义典型侧倾和典型俯仰转移姿态着陆平台本体坐标系（O-XYZ）及相关参数，如图 3~4所示[12-13]。

图3 典型侧倾转移姿态Fig.3 Typical roll transfer attitude

图4 典型俯仰转移姿态Fig.4 Typical pitch transfer attitude

坐标原点O：着陆平台上表面的中心；

X轴：过坐标原点，以火星车转移方向为正；

Z轴：过坐标原点，垂直于着陆平台上表面，指向火星车为正；

Y轴：与X轴、Z轴构成右手坐标系；

Α为地形角，表征着陆平面与水平面夹角，且不超过8°；

β为俯仰角，表征着陆平台绕+Y轴旋转所成的倾角，且不超过6°；

δ为侧倾角，表征着陆平台绕+X轴旋转所成的倾角，且不超过6°；

ψ为方位角，表征着陆平台整体绕Z轴的转角，侧倾姿态方位角为0°，俯仰姿态方位角为-90°；

h为局部地貌，表征坡道触地端可能遇到的岩石或凹坑，且不超过200 mm；

L为坡道长度；

θ为转移坡度角，转移坡道面π与水平面夹角的最大值，按火星车安全转移要求不超过30°；

γ为异面角，接触地面后两条坡道间的夹角，按火星车安全转移要求不超过8°。

2.2 转移姿态分析数学模型建立

转移坡度角θ和坡道异面角γ决定于L、α、β、δ、ψ、h的取值，根据技术要求，坡道展开后，两侧坡道形成的转移坡道面与当地水平面之间的夹角不大于30°，两侧坡道间异面角不大于8°。综合考虑转移姿态不确定的三方面因素，坡道长度应使各种转移姿态下的转移坡度角θ和坡道异面角γ均满足约束条件。为简化数学模型建立的难度，由于俯仰角β只会减小或不影响转移坡度角和坡道异面角，因此在数学模型中不考虑俯仰角的影响。基于空间解析几何理论，以转移坡度角θ和坡道异面角γ为目标函数，以着陆平面与当地水平面夹角α、着陆平台侧倾角δ、着陆区域局部地貌h、着陆平台构型尺寸等为参数化变量，分别建立典型侧倾和典型俯仰转移姿态坡道长度参数化分析模型。将着陆平台简化成长方体，坡道简化成空间两条线段，着陆平台侧倾和俯仰坡道长度分析模型如图 5～6所示。O点：简化长方体的顶点；Y轴：两坡道根部铰链安装点所在直线；Z轴：垂直于长方体顶面；X轴：过O点与Y轴、Z轴构成右手系。

图5 侧倾姿态坡道长度分析模型Fig.5 Ramp length analysis model of typical roll transfer attitude

图6 俯仰姿态坡道长度分析模型Fig.6 Ramp length analysis model of typical pitch transfer attitude

在图 5坐标系下表示AB坡道与火星接触面π1、CD坡道与火星接触面π2、线段AB和CD的方程。

平面π1方程为

平面π2方程为

其中：r与δ相关的量，δ≥0时取1，反之取0；h1表征AB遇到的局部地貌；h2表征CD遇到的局部地貌；d表征着陆平台宽度；b表征着陆平台距着陆平面距离。

点B是以A为圆心，以坡道长度L为半径的圆与平面π1的交点坐标，点D是以C为圆心，以坡道长度L为半径的圆与平面π2的交点坐标，两圆方程分别为

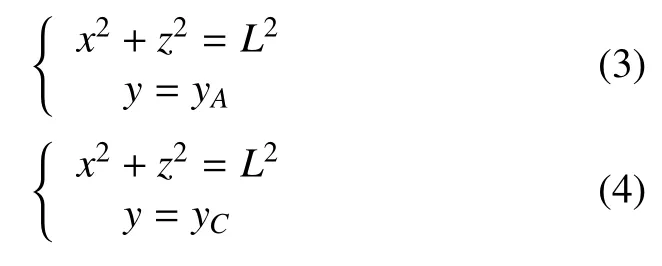
其中：L为坡道长度；yA点A沿Y轴坐标；yC是C点沿Y轴坐标。

联立式（1）～（4），解得B、D点坐标

利用点A、点B的坐标容易得出直线AB方程为

利用点C和点D的坐标容易得出直线CD方程为

定义转移坡道考核面π：

1）线段AB上的各点分别与线段CD构成的平面；

2）线段CD上的各点分别与线段AB构成的平面。如在线段AB上取点P，利用线段AB方程得到P点坐标，CD方向向量AB方向向量则转移坡道考核面π的法向量及当地水平面法向量分别为

给定侧倾角δ、局部地貌h1、h2、坡道长度L、着陆平台构型尺寸等相关参数后，转移姿态即确定，求得所有考核平面π与当地水平面π3之间的夹角的最大值即为当前转移姿态下转移坡度角θ为

坡道异面角γ与转移坡道考核面π选取无关，为

3 最小坡道长度及极限转移姿态确定

综合考虑典型侧倾、典型俯仰转移姿态，着陆平台极限侧倾角（0°、-6°、+6°）、局部地貌h1、h2（有5种情况）、地形角α（8°）的所有组合，组合得到30种转移姿态。根据前文建立的数学模型，利用matlab编制坡道长度分析程序，输入地形角α、侧倾角δ、局部地貌h1、h2、着陆平台构型尺寸等相关参数后，获得30种转移姿态下，转移坡度角θ和坡道异面角γ随坡道长度的变化曲线。根据曲线得到30种转移姿态下满足θ、γ取值条件的最小坡道长度。满足条件的所有最小坡道长度达到最大值时对应的转移姿态即为极限转移姿态。图 7～8中线1是异面角γ≤ 8°对坡道长度可行域的约束，线2是转移坡度角θ≤ 30°对坡道长度可行域的约束。分析结果表明，15种侧倾姿态下，当α= 8°、δ= 0°且AB遭遇0.2 m凹坑时，最小坡道长度达到最大值2.98 m，该极限转移姿态下θ-L、γ-L曲线如图7所示。15种俯仰姿态下，当α= 8°、δ= 0°且任一侧坡道遭遇0.2 m凹坑时，最小坡道长度达到最大值3.47 m，该姿态下θ-L、γ-L曲线如图 8所示。综上分析所述，满足火星车安全转移条件的最小坡道长度为3.47 m，所对应的极限转移姿态如图 8中所示。

图7 侧倾姿态下的极限转移姿态θ-L、γ-L曲线Fig.7 Limit transfer attitude of typical roll attitudeθ-L、γ-Lcurves

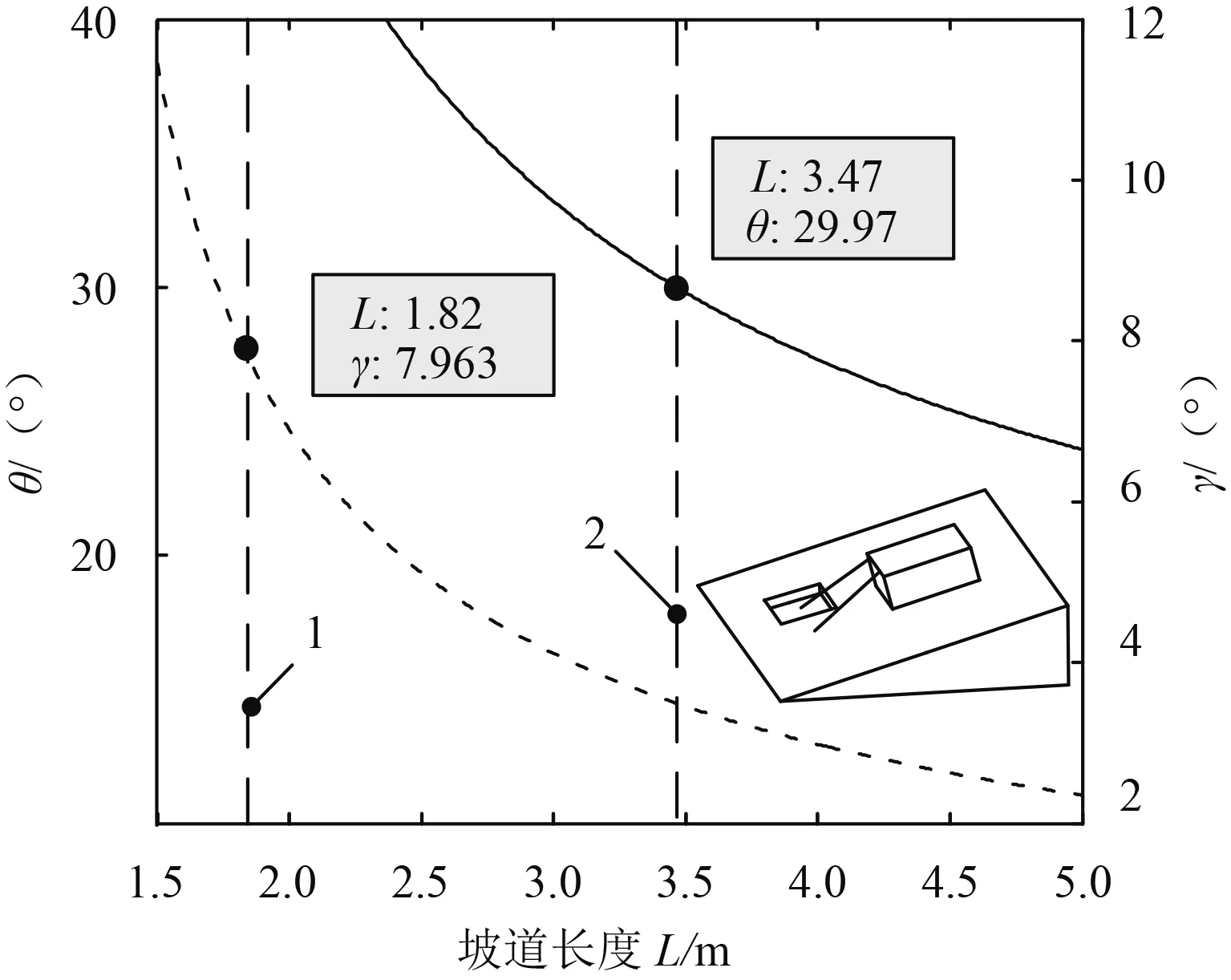
图8 俯仰姿态下极限转移姿态θ-L、γ-L曲线Fig.8 Limit transfer attitude of typical pitch attitudeθ-L、γ-Lcurves

4 三折平展坡道长度优化

为了使三折坡道展开总长度尽可能靠近最小坡道长度3.47 m的需求，进行三折坡道铰链点B、C位置优化，获得在着陆器构型约束下三折坡道长度最大值。三折坡道长度优化示意图如图 9所示，优化目标函数为三段坡道长度达到最大值。

图9 三折坡道长度优化示意图Fig.9 Diagram for ramp length optimization of tri-folded and deployed type ramp

其中：β优化设计参数，AB与AD夹角。

其中：R为坡道回转铰链外接圆半径；h为根部铰链连接线到平台圆心间距；AD为根部铰链连接线弦长。

弦长AB、BC为

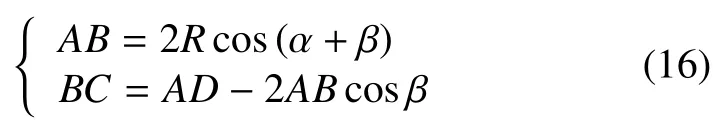
其中：α为D与OA夹角。

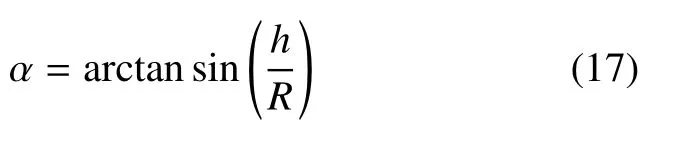
根据上述数学模型，利用matlab编制程序，输入相关参数后，获取三折坡道长度L-β关系曲线如图 10所示，根据该曲线可知，当β大小为43.1°，坡道长度达到最大值为3 084 mm。从而可以确定出铰链点B、C位置。可见三折平展坡道转移方案能获得的最大坡道长度3 084 mm仍小于最小坡道长度3.47 m。在3 084 mm坡道长度下，火星车能否在极限转移姿态下安全转移尚需进行地面试验验证。

图10 三折坡道长度L-β关系曲线Fig.10 Ramp lengthL-βcurve of tri-folded and deployed type ramp

5 结 论

本文针对基于着陆平台的火星车转移任务，提出了一种三折平展坡道转移方案。本文开展的分析及结论如下：

1）基于空间解析几何理论，建立了火星车坡道式转移姿态分析数学模型，综合分析了30种转移姿态，得到满足火星车安全要求的最小坡道长度为3 470 mm，并确定了火星车极限转移姿态，上述分析结果，能为火星车坡道式转移方案设计和坡道式转移地面试验验证的转移姿态设定提供理论依据。

2）针对所提出的三折平展坡道方案，进行了坡道长度优化分析，结果显示，该方案下坡道所能达到的最大长度为3 084 mm。研究工作能为我国火星车转移工程实施提供借鉴。

[1]叶培建，彭兢.深空探测与我国深空探测展望[J].中国工程科学，2006，8（10）：13-18.Ye P J，Peng J.Deep space exploration and its prospect in China[J].Engineering Sciences，2006，8（10）：13-18.

[2]吴伟仁，于登云.深空探测发展与未来关键技术[J].深空探测学报，2014，1（1）：5-17.Wu W R，Yu D Y.Development of deep space exploration and its future key technologies[J].Journal of Deep Space Exploration，2014，1（1）：5-17.

[3]侯欣宾，王立.我国火星探测发展设想[C]//中国宇航学会深空探测技术专业委员会学术年会.三亚：宇航学会，2010.Hou X B，Wang L.The proposed Mars exploration roadmap in China[C]// Annual Conference of the Deep Space Exploration Technology of Chinese Astronautical Society.Sanya：Chinese Astronautical Society，2010.

[4]朱仁璋，王鸿芳，泉浩芳，等.美国火星表面探测使命述评（上）[J].航天器工程，2010，19（2）：17-33.Zhu R Z，Wang H F，Quan H F，et al.Overview of the US Mars surface missions（Part One）[J].Spacecraft Engineering，2010，19（2）：17-33.

[5]朱仁璋，王鸿芳，泉浩芳，等.美国火星表面探测使命述评（下）[J].航天器工程，2010，19（3）：7-27.Zhu R Z，Wang H F，Quan H F，et al.Overview of the US Mars surface missions（Part Two）[J].Beijing：Spacecraft Engineering，2010，19（3）：7-27.

[6]韩鸿硕，王一然，蒋宇平，等.国外深空探测器着陆缓冲系统的特点和应用[J].航天器工程，2012，21（06）：7-24.Han H S，Wang Y R，Jiang Y P，et al.Characterisitics and application of deep-space explorer landing impact attenuation system[J].Spacecraft Engineering，2012，21（06）：7-24.

[7]韩鸿硕.21世纪国外深空探测发展计划及进展[J].航天器工程，2008，17（3）：1-22.Han H S.21st century foreign deep space exploration development plans and their progresses[J].Beijing：Spacecraft Engineering，2008，17（3）：1-22.

[8]陈哲吾，文桂林，卿启湘，等.月面巡视器转移机构方案研究[J].机械科学与技术，2012，31（11）：1754-1759.Chen Z W.Wen G L，Qing Q X，et al.Research of the transport mechanism for the Lunar rover[J].Mechanical Science and Technology for Aerospace Engineering，2012，31（11）：1754-1759.

[9]方宝东，王伟，李金环，等.火星着陆器方案设想[C]//中国宇航学会深空探测技术专业委员会学术年会.三亚：宇航学会，2010.Fang B D，Wang W，Li J H.The Mars landing exploration probe system project study[C]//Annual Conference of the Deep Space Exploration Technology of Chinese Astronautical Society.Sanya：Chinese Astronautical Society，2010.

[10]彭玉明，李爽，满益云，等.火星进入、下降与着陆技术的新进展--以“火星科学实验室”为例[J].航天返回与遥感，2010，31（4）：7-14.Peng Y m，Li S，Man Y Y，et al.New progress of Mars entry，descent and landing technologies-Mars science laboratory case study[J].Spacecraft Recovery & Remote Sensing，2010，31（4）：7-14.

[11]刘宾，李新立，柴洪友，等.“嫦娥3号”着陆平台释放与转移巡视器技术[J].中国科学：技术科学，2014（6）：576-581.Liu B，Li X L，Chai H Y，et al.Rover release and transfer techniques of Chang’E-3 probe’s lander[J].Sci Sin Tech，2014，44：576-581.

[12]郑宝东.线性代数与空间解析几何[M].北京：高等教育出版社，2008.Zheng B D.Linear algebra and space analytic geometry[M].Beijing：Higher Education Press，2008.

[13]孙靖民，梁迎春.机械优化设计[M].北京：机械工业出版社，2006.12.Sun J M，Liang Y C.Mechanical optimum design[M].Beijing：Machinery Industry Press，2006.

Analysis on Transfer Attitude of Tri-Folded and Deployed Type Ramp for Mars Rover

LIU Wei1，QIAN Cheng2，MA Chao2，JIANG Shengyuan2
（1.Beijing Institute of Spacecraft System Engineering，Beijing 100090，China；2.State Key Laboratory for Robotics and System，Harbin Institute of Technology，Harbin 150080，China）

For landing on Mars for inspection detection，a tri-folded and deployed ramp is proposed to transfer the Mars rover from the landing platform to the Mars surface safely.The uncertainty of the transfer attitude is the difficulty of tri-folded and deployed ramp.The minimum length of ramp is analyzed according to Martian topography to ensure the transfer safety of Mars Rover.The length of tri-folded and deployed ramp is optimized to meet the requirements of the minimum length of ramp.The results can provide reference for the mars rover transferring project of China.

landing on Mars for inspection detection；ramp；analysis on transfer attitude；optimization

V423.6

A

2095-7777（2017）03-0287-06

[责任编辑：高莎，英文审校：朱鲁青]

10.15982/j.issn.2095-7777.2017.03.014

刘卫，钱成，马超，等.火星车三折平展坡道转移方案及转移姿态分析[J].深空探测学报，2017，4（3）：287-292.

Reference format：Liu W，Qian C，Ma C，et al.Analysis on transfer attitude of tri-folded and deployed type ramp for Mars rover[J].Journal of Deep Space Exploration，2017，4（3）：287-292.

2017-04-11

2017-05-30

刘卫（1984- ），男，工程师，主要研究方向：宇航空间机构设计。

地址：北京市海淀区友谊路104号（100094）

电话：（010）68746809

E-mail：24048774@qq.com

姜生元（1969- ），男，教授，博士生导师，主要研究方向：深空采样探测技术、宇航空间机构及控制技术。本文通信作者。

通信地址：哈尔滨工业大学科学园2F栋403室（3037信箱）（150080）电话：13796621169

E-mail：jiangshy_2002@163.com