基于不变流形的地-月L2点转移轨道优化设计
安然,王敏,梁新刚
(中国空间技术研究院 通信卫星事业部,北京 100094)
基于不变流形的地-月L2点转移轨道优化设计
安然,王敏,梁新刚
(中国空间技术研究院 通信卫星事业部,北京 100094)
在地-月L2点月球中继卫星轨道转移设计中,采用高比冲、小推力的电推进器可以大大增加卫星的有效载荷比,但会增加轨道设计的难度。基于地球GEO轨道为初始轨道,地-月L2点的halo轨道为目标轨道,通过最优控制中的混合法及平动点轨道的不变流形,研究了作为拓展任务的利用地月系统不变流形的小推力变轨方案,可以有效简化转移的轨道设计。仿真结果表明:得到了任意推力情况下最节省推进剂燃料的推力方向控制方案,对月球中继卫星的轨道设计及其平动点轨道设计具有工程意义。
电推进;最优控制;混合法;小推力;平动点
0 引 言
位于平动点附近的周期或拟周期轨道可为多种探测任务或中继通信任务提供良好的工作场所。地-月L2的(拟)周期轨道是为位于月球背面的探测卫星提供通信中继的最佳场所。由于月球自转与公转速度相同,月球背面始终处于对地不可见的阴影区域。而地-月L2点位于地-月连线,并且一颗星可以实现对月球背面平均87.6%区域的覆盖。无论是通信卫星寿命末期进行的试验拓展任务,或是基于月球背面探测器的中继需要,研究从GEO轨道出发到地-月L2点的转移轨道都是必要的。
电推进技术通过电能驱动工质高速喷出获得推力,具有高比冲、低推力和长寿命等特点[1-3]。目前越来越多的地球静止轨道卫星开始配置电推力器执行轨道转移及位置保持等任务。全电推卫星的有效载荷质量比采用传统化学推进剂的有效载荷质量比高,故而在位于GEO的通信卫星寿命末期,可以考虑进行深空拓展任务,以完成短时期的探测任务或是深空探测试验验证任务。
目前国际上尚未利用电推进进行平动点探测的卫星任务,这主要是由于虽然利用电推进器可以增加有效载荷比,但却使得轨道任务设计的难度大大增加。并且地-月系统相较于日-地系统而言,地球处于圆形限制性三体模型中大天体的位置,使得地-月系统平动点的不变流形与近地轨道并无相交,必须进行近地段的小推力上升变轨设计。本文建立了地-月系统不变流形与上升段的拼接坐标系转换方法,并完成了小推力转移段设计。
1 不变流形设计及计算
不变流形与平动点周期轨道紧密相连,它是一族空间轨道的集合,在空间中形成管状通道。不变流形分为稳定流形与不稳定流形,稳定流形上的质点会自发地趋近于周期轨道[4],所以利用稳定流形进行轨道转移可以节省燃料。将halo轨道上任意一个不动点积分一个周期后得到的状态转移矩阵称为单值矩阵[5],通过计算单值矩阵中小于1的特征值对应的特征向量Vs,得到稳定流形

其中:d为设计参数,对于月球中继卫星,可取50 km[6]。
halo轨道上的不动点通过相位角描述,每一不动点对应两条不变流形,halo轨道所有不动点的稳定流形及组成了周期轨道的稳定流形管道,如图 1所示。
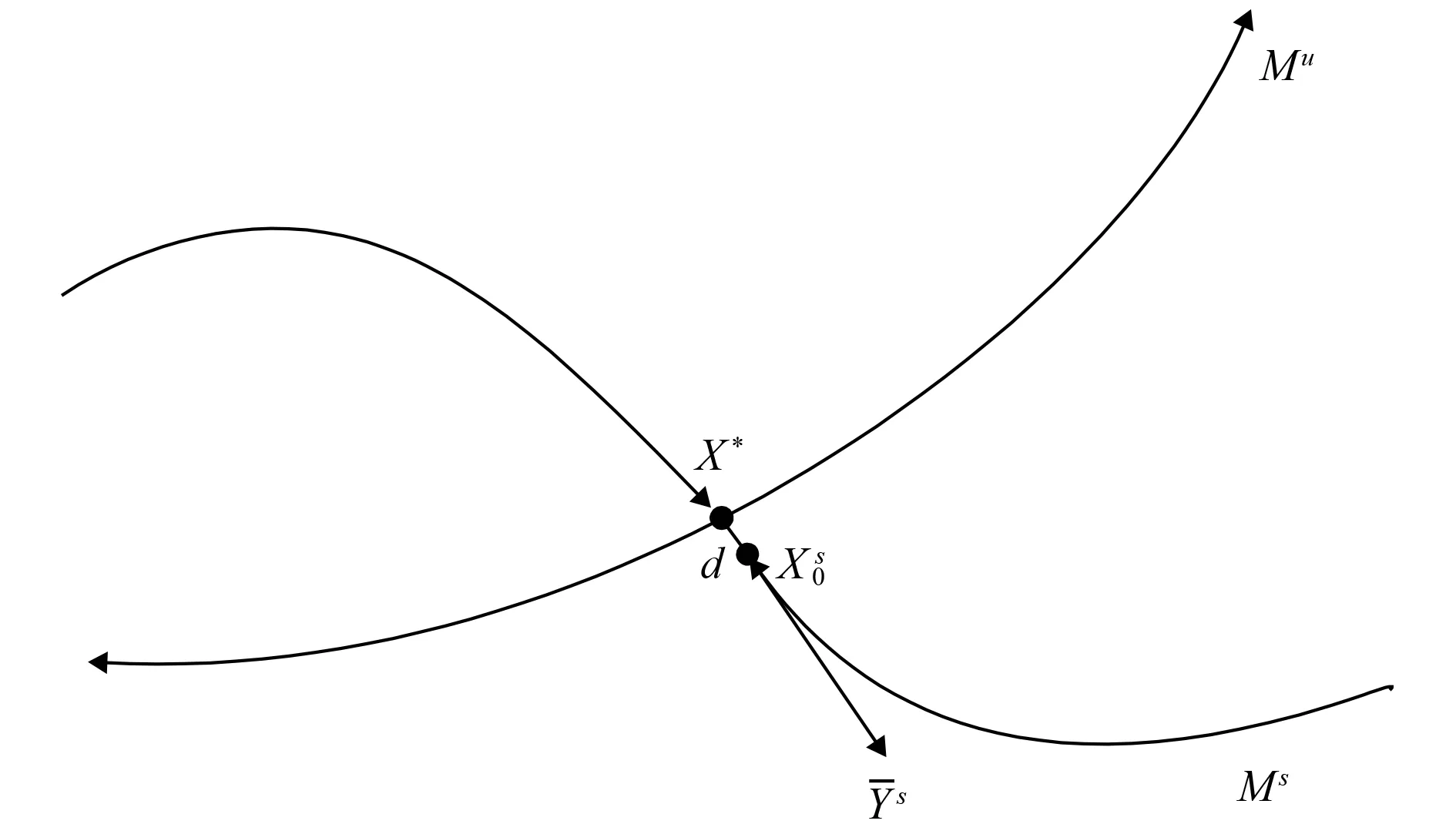
图1 X点的不变流形Fig.1 Invariant manifold of X
由于不变流形是在圆形限制性三体模型的会合坐标系中求解计算的,在进行小推力转移轨道的拼接设计时,需要把会合坐标系中的不变流形转换到地球J2000惯性坐标系中。在位置转换时,首先求出卫星在高精度会合坐标系下相对地球的位置,而后完成高精度星历会合坐标系向惯性坐标系旋转,最后将归一化单位转化为国际单位制。得到位置转换关系为

其中:x、y、z为卫星在会合坐标系中的位置坐标;xi、yi、zi为卫星在地球J2000惯性坐标系中的位置坐标;i、Ω、ω、θ分别代表月球在地球J2000坐标系下的实时轨道倾角、升交点赤经、近地点角距、真近点角;D为圆形限制性三体模型中会合坐标系的归一化长度单位;R为归一化地月实时距离。
计算速度转换时,需要考虑牵连速度及卫星相对地球的相对速度,再完成坐标系旋转及单位转化,得到速度转换关系

其中:ω为归一化单位下瞬时旋转角速度;为瞬时平动点的速度;为月球速度;为圆形限制性三体模型中会合坐标系的归一化时间单位。
2 基于混合法的改进春分轨道根数小推力优化方程
改进春分点轨道根数模型在小推力转移变轨中只在i=180°时,会出现奇异,优于笛卡尔模型及经典轨道根数模型,所以采用改进春分点轨道根数模型进行小推力变轨优化设计,模型定义为[7]
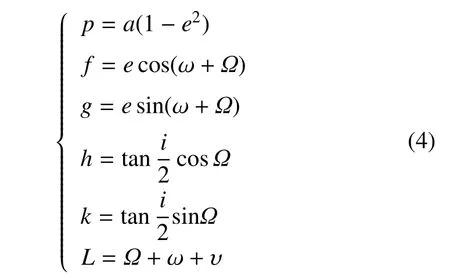
2.1 混合法
通过运用极小值原理,轨迹优化问题最终会转化为一个由正则方程组、初始与终端物理边界及横截条件构成的两点边值问题,通过求解该两点边值问题可以得到轨迹优化问题的解,这种方法成为间接法。协状态方程组对协状态初始猜测高度敏感,协状态初始猜测与其真实值要足够接近问题才能收敛,不“好”的初始猜测会导致数值积分中断,使得求解过程无法继续,问题收敛半径非常小。而协状态本身没有物理意义,很难提供足够“好”的初始猜测,所谓“好”是指足够地接近真实值。大量的研究文献与数值计算实验表明,在当前技术条件下,求解该两点边值问题是一件极其困难的工作,特别是发动机开关机次序受开关函数控制的两点边值问题[8]。
一些学者放弃对两点边值问题的求解,转而使用所谓的“混合法”对轨迹优化问题进行求解。混合法将轨迹优化问题转化为针对协状态初值(及其它诸如开关机时刻等系统参数)的参数优化问题,只满足初始与终端物理边界约束,不考虑横截条件,通过合适的非线性规划算法求解。性能指标的最优性由非线性规划算法保证。一方面,混合法引入协状态,利用正则方程组的结构,可以得到光滑的控制;另一方面,它不去求解两点边值问题,不考虑横截条件,减少了终端约束,增大了收敛半径。
由轨迹优化问题得到正则方程组后,若任意给定一组协状态初始值及其它相关参数β,通过数值积分积到tf时刻,即可得到一组终端状态进而得到Mayer型性能指标。因此,可以将性能指标与终端状态都看作是协状态初值与未知参数β的函数。这样,轨迹优化问题可以转化为针对未知参数与β的参数优化问题。即:寻找参数与β,使性能指标J最小

同时满足物理终端约束

混合法只考虑物理终端约束,不考虑由横截条件得到的对协状态终值的约束。由式(5)与式(6)构成了针对与β的参数优化问题,可以通过合适的非线性规划算法进行求解,性能指标的最优性由非线性规划算法保证。而且,除式(6)表示的等式约束外,还可以将不等式约束包含到问题的求解过程中。混合法无法由开关函数确定精确的开关次序,需要事先人为指定开关次序,将开关机时刻作为未知参数去优化。参数β表示除协状态初值外的所有系统未知参数,如发动机开、关机时刻,未知终端时刻等。
2.2 小推力优化方程
春分点根数描述的动力学方程可表示为

矩阵B为


利用控制方程,可得到最优控制推力方向为[9]

对哈密顿函数对状态求偏导数,得到共轭方程为

对小推力变轨优化问题,动力学方程式(5),共轭方程式(9)和边界条件组成一个参数优化问题。求解参数优化问题可得到卫星的最优飞行轨迹,同时获得共轭状态的变化轨线。通过控制方程可确定式(8)相应的最优控制轨线。本文采用非线性规划算法求解上述参数优化问题,以协状态量初值作为优化变量,以小推力轨道转移时间最短作为优化目标。基于改进春分点根数的小推力混合优化法原理如图 2。
3 数值仿真
对于电推进的平动点轨道转移任务,通过利用地-月L2点飞行轨道的不变流形,航天器在转移轨道中,只要进入不变流形即可以熄火,所以小推力转移弧段的末状态即为不变流形中任一点的位置与速度。考虑时间最优方案,电推进器持续点火,比冲恒定,通过调节俯仰角和偏航角得到最优的转移方案。
3.1 滑行段轨道设计
在圆形限制性三体模型下一个周期的halo轨道上,选取按时间均分的50个不动点。在每一点处将动力学方程线性化,求出不动点积分一个周期后的单值矩阵。以t=0时刻的不动点为例,单值矩阵的特征值为

λ2为t=0时刻不动点的稳定特征值λs,对应的特征向量Vs为该不动点的稳定特征向量。通过式(1)可求出该不动点对应的稳定流形的出口点。
通过对50个不动点分析计算即可得到全部的稳定流形出口点,动力学积分后即可得到全部的稳定流形。同理也可以求出所有的不稳定流形。
地-月系L2点halo轨道的稳定流形及如图 3所示,积分时间约为30 d。
返回的路上,经过一条很深的过山渠,猪牯见鬼一样跑到渠边,前腿梭地往下滑,我父亲眼疾手快拽住猪尾巴,再慢慢去够它的后腿,结果是猪一蹬上来了,我父亲却失去重心掉了下去。摔得很惨,抢救一天一夜,命总算保住了,可人全身瘫痪,话也说不清楚。当初抢救时,迷迷糊糊的,他倒是说过几段经典的胡话,一是说猪牯够浪漫想采花呢,二是说新厕够气派那么多蹲位象征生源充足呀,三是问那个东家会叫县中老师重新写过春联吗,还叮嘱我,讲义夹里记下的人家将来记得要一一拜访。这句不算胡话,应是遗嘱,管了猪生仔还不够呀,还要管它们瓜瓞绵绵吗?

图2 小推力混合优化法示意图Fig.2 Low-thrust hybrid optimal design algorithm

图3 地-月系L2点halo轨道的稳定流形Fig.3 Stable manifold of L2 halo orbit
图中绿色实点表示地球及月球的位置,红色实点为地-月系L1的位置,红色实线为地-月系L2点附近垂直幅值为5 000 km的halo轨道,蓝色实线为halo轨道的稳定流形。
通过对该稳定流形进行分析,发现稳定流形分两支:一支靠近地球,一支远离地球。取其中靠近地球的一族流形轨道,如图 4,绿色实点表示地球及月球,红点表示L1及L2点。
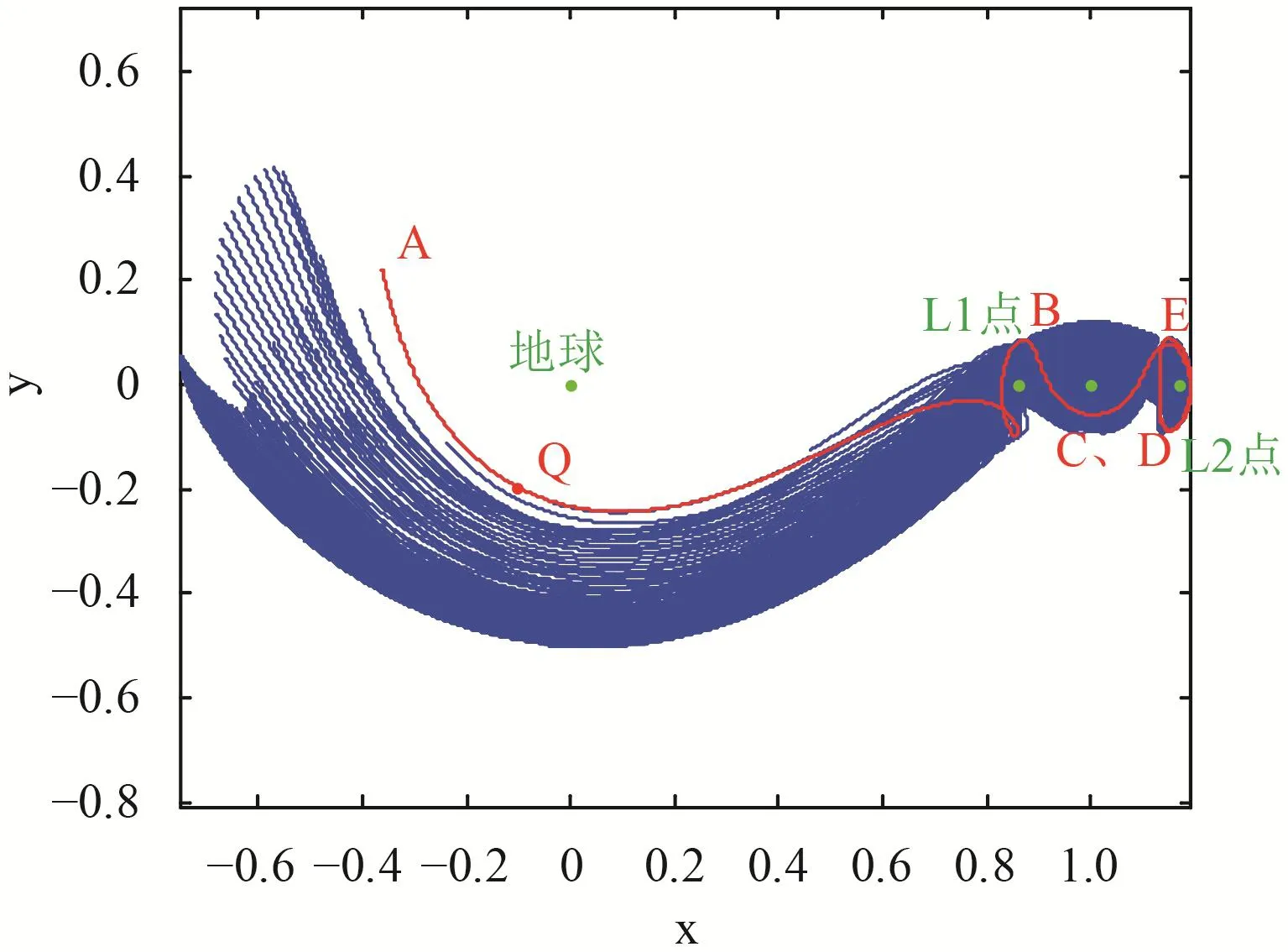
图4 地-月系L2点一类halo轨道的稳定流形Fig.4 A cluster of stable manifold for L2 halo orbit
末状态为不变流形中的不动点,采用不变流形的设计方法,求得地-月L2点附近幅值为5 000 km的halo轨道不变流形中离地球距离最近的一点Q,将不动点从圆形限制性三体模型会合坐标系转换到地球J2000惯性坐标系下,得到入口点的位置速度信息为

3.2 小推力上升段轨道设计
在轨道动力学积分时,应尽量避免出现奇点,所以轨道动力学模型选为改进春分点根数模型。控制量为俯仰角、偏航角;状态量为位置、速度及质量;协状态量为位置、速度及质量对应的协状态量。
初始轨道选用地球静止轨道,正则距离单位选为42 164 km,初始轨道经过单位正则化后

不对真近点角进行约束。比冲为3 000 s,g选为9.81 m/s2。末状态位置即为式(13)的不变流形入口点的位置速度信息。
真近点角的初值选择区间为0°~360°,质量初值为1,协状态初值选择区间为-1~1的任意实数。
根据前文介绍的基于混合法的小推力优化方程,分别求出初始推力加速度为0.000 4 m/s2(1 t卫星400 mN推力)至初始推力加速度为0.000 8 m/s2(1 t卫星600 mN推力)的时间最优转移方案,并列出所需时间、推进剂消耗(卫星质量为1 t)如表 1。

表1 小推力最优转移方案对比Table 1 Cooperation of low-thrust transfer trajectory optimal design
从表 1数据可以得知,当卫星质量已知时,推力越大,转移轨道所需时间越少。而推进剂消耗质量随着推力自大而小的变化先减小后增大,这是由于电推进推力减小到一定程度后,摄动力对卫星的影响增加,从而使得卫星消耗了较多的推进剂。把推力大小同样作为优化目标进行转移轨道设计,得到推进剂消耗最少时对应的推力初始加速度为0.000 623 m/s2,即卫星质量为1 t时,推力器为623 mN,最节约推进剂。
以电推进器初始推力加速度为0.000 4 m/s2为例,由于电推进系统推力大小恒定,示意控制量即电推进器的推力方向变化随时间变化如图 5所示。

图5 控制量随时间变化示意图Fig.5 Governing variables
半长轴、偏心率、轨道倾角、质量等主要状态量随时间变化如图 6。

图6 状态量随时间变化示意图Fig.6 State variables
电推进器初始推力加速度为0.000 4 m/s2时,J2000坐标系下的轨道转移过程如图 7所示。

图7 J2000坐标系下的轨道转移过程Fig.7 Transfer trajectory in the Earth J2000 coordinate system
通过对地-月L2点的月球中继卫星的转移轨道仿真,可以得到近地上升段的小推力转移方案,卫星轨道转移至不变流形后,关闭电推进器,卫星可以沿不变流形进入地-月L2点附近的halo轨道内,从而进行月球中继的通信任务。
4 结 论
本文以通信卫星为研究对象,通过最优控制原理中的混合法计算了以月球中继任务为拓展任务的GEO轨位通信卫星轨道转移优化方案。得到卫星质量为1 t时,从地球GEO同步轨道出发时的时间最优转移方案并给出卫星俯仰角及偏航角随时间的变化关系,为获得工程上切实可用的月球中继卫星转移轨道提供了有益借鉴。
[1]刘江,赵宏.卫星电推进应用技术现状及发展[C]//第十二届空间及运动体控制技术学术年会.北京:自动化学会.2006.Liu J,Zhao H.Present situation and development of application of satellite electric propulsion[C]// The 12th Annual Conference on Space and Motion Control Technology.Beijing:Automation Society,2006.
[2]魏延明.国外卫星推进技术发展现状与未来20年发展趋势[J].航天制造技术,2011(2):7-12.Wei Y M.Current situation and developing direction of foreign satellite propulsion technology in the next 20 years[J].Aerospace Manufacturing Technology,2011(2):7-12.
[3]温正,王敏,仲小清.多任务模式电推进技术[J].航天器工程,2014,23(1):118-123.Wen Z,Wang M,Zhong X Q.Multitask mode electric propulsion technologies[J].Spacecraft Engineering,2014,23(1):118-123.
[4]Anderson R L,Martin W L.Role of invariant manifolds in low-thrust trajectory design[J].Journal of Guidance Control and Dynamics,2009,32(6):1921-1930.
[5]Folta D C,Pavlak T A.Earth-Moon libration point orbit station keeping: theory, modeling, and operations[J].Acta Astronautica,2014,94(1):421-433.
[6]Zhou J,Xue L,Zhou F Q.Computations of low energy escaping/ capturing trajectories in hill's region via an extended poincaré map[J].Journal of Astronautics,2007,28(3):643-647.
[7]王青,陈宇,张颖昕,等.最优控制-理论、方法与应用[M].北京:高等教育出版社,2011.Wang Q,Chen Y,Zhang Y X,et al.Optimal control-theory,method and applications[M].Beijing:Higher Education Press,2011.
[8]梁新刚.面向两类空间对抗任务的轨道优化设计方法研究[D]哈尔滨:哈尔滨工业大学,2008.Liang X G.Research on orbit optimization design method for two kinds of space confrontation tasks[D].Harbin:Harbin Institute of Technology,2008.
[9]崔平远,乔栋,崔祜涛.深空探测轨道设计与优化[M].北京:科学出版社,2014.Cui P Y, Qiao D,Cui H T.Orbital design and optimization of deep space exploration mission[M].Beijing:Science Press,2014.
Transfer Trajectory Optimal Design for Earth-Moon L2 Based on Invariant Manifolds
AN Ran,WANG Min,LIANG Xingang
(Institute of Telecommunication Satellite,China Aerospace Science and Technology Corporation,Beijing 100094,China)
During the optimal design of transfer trajectory to translunar libration point,the payload launch capacity of Lunar Relay Satellite can be improved greatly if the electric thrusters which have high specific impulse and low thrust can be used as main propulsion.The optimal design of low-thrust transfer trajectory is studied which makes use of the invariant manifolds of Earth-Moon system based on the hybrid method.GEO is the initial orbit and halo orbit around translunar libration point L2 is the aim orbit of the transfer trajectory.The simulation result shows that thruster direction control strategy which consumes the least propellant for transfer trajectory has been obtained.The result is of great important engineering meaning.
electric thruster;optimal control theory;hybrid method;low-thrust transfer;translunar libration point
V412.4+1
A
2095-7777(2017)03-0252-06
[责任编辑:高莎,英文审校:朱鲁青]
10.15982/j.issn.2095-7777.2017.03.008
安然,王敏,梁新刚.基于不变流形的地-月L2点转移轨道优化设计[J].深空探测学报,2017,4(3):252-257.
Reference format:An R,Wang M,Liang X G.Transfer trajectory optimal design for Earth-Moon L2 based on invariant manifolds[J].Journal of Deep Space Exploration,2017,4(3):252-257.
2017-03-20
2017-06-01
安然(1993- ),女,硕士,主要研究方向:地-月L2点的轨道设计。
通信地址:北京市海淀区友谊路102号院青年公寓(100094)
电话:(010)68745369
E-mail:emma1270789119@163.com

