应用稳健统计方法对环境空气臭氧自动监测现场比对核查结果的分析研究

师耀龙，杨 婧，姚雅伟，李 成，滕 曼，柴文轩，楚宝临，付 强

1.中国环境监测总站,国家环境保护环境监测质量控制重点实验室，北京 100012 2.河北农业大学科学技术研究院,河北 保定 071001

应用稳健统计方法对环境空气臭氧自动监测现场比对核查结果的分析研究

师耀龙1，杨 婧1，姚雅伟1，李 成2，滕 曼1，柴文轩1，楚宝临1，付 强1

1.中国环境监测总站,国家环境保护环境监测质量控制重点实验室，北京 100012 2.河北农业大学科学技术研究院,河北 保定 071001

根据2015年9个城市53台现场臭氧分析仪的现场比对核查结果，比较研究了稳健统计方法和一般统计方法在评价国控网臭氧自动监测数据准确性和精密性上的应用。研究表明：稳健统计能够在不剔除异常数据的前提下降低异常值对正确评价臭氧自动监测数据质量的影响，适合评价现场比对核查结果；采用Hubers方法进行稳健统计，2015年国控网臭氧日常浓度点相对偏差的95%置信区间约为-0.1%至4.5%，95%预测区间为-14.0%～18.3%，变异系数约为9.5%，数据质量仍有提升空间。

环境空气监测；臭氧；现场比对核查；稳健统计

根据新修订的《环境空气质量标准》(GB 3095—2012)中增设的臭氧8 h滑动平均限值，各级环保部门需开展环境空气臭氧自动监测工作。由于目前没有标准钢瓶气体能够用于臭氧自动监测设备的现场比对，采用臭氧传递标准与现场臭氧分析仪进行现场比对成为评价臭氧自动监测数据质量的有效手段[1]。如何汇总现场比对结果进行统计分析，科学、客观地评价臭氧自动监测的数据质量，成为困扰各级环境监测机构的新问题。

目前我国环境监测系统尚未出台汇总臭氧现场比对结果评价固定周期内某点位现场分析仪或相关区域内臭氧监测数据质量的统计方法。美国在其联邦法规中规定，通过计算固定周期内现场比对结果的标准偏差的90%置信区间(变异系数)和中心值的95%置信区间(偏倚)可分别评价其数据精密性和准确性[2]，此方法值得我国借鉴。但是，美国环保局用于区间估计的中心值和标准偏差为平均值和一般标准偏差，对数据符合正态分布的假定有很强的依赖性，其方法稳健性较差。当出现严重偏离实际中心值的异常数据时，其计算得到的中心值和标准偏差可能严重偏离实际的中心值和标准偏差，无法正确计算臭氧自动监测数据的精密度与偏倚。因此，需对传统统计方法进行稳健化以适应实际工作的需要。

本文基于2015年中国环境监测总站(以下简称“总站”)开展的臭氧自动监测现场比对核查结果，结合稳健统计方法，初步评价了国控网现阶段臭氧自动监测数据质量。同时，对如何科学、统一、可行的评价臭氧自动监测数据质量进行了初步的探讨。

1 实验部分

1.1臭氧自动监测现场比对核查方法

总站在2015年对9个重点城市共计53台现场臭氧分析仪进行了现场比对核查，具体方法：携带经臭氧标准参考光度计校准过的臭氧传递标准至臭氧自动监测现场，分别发生零气、日常浓度(上一年小时数据均值)、100×10-9mol/mol和400×10-9mol/mol的臭氧，同时记录臭氧传递标准与现场臭氧分析仪的读数，计算日常浓度点、100×10-9mol/mol和400×10-9mol/mol浓度点的相对偏差，计算零点的偏差。具体操作参考《国家环境监测网环境空气臭氧自动监测现场核查技术规定》。

1.2统计方法

1.2.1 传统统计方法

将53台现场分析仪的日常浓度点、100×10-9mol/mol和400×10-9mol/mol浓度点的相对偏差以及零点的偏差汇总后进行进一步的统计分析。使用统计软件R绘制4个浓度点的核密度图和直方图。根据Shapiro-Wilk模型分别检验4个浓度点的数据是否符合正态分布。

根据美国联邦法规中[2]规定的臭氧自动监测数据质量评价公式计算各浓度点偏差/相对偏差的变异系数(CV)、95%置信区间(偏倚，bias)和95%预测区间。变异系数计算公式：

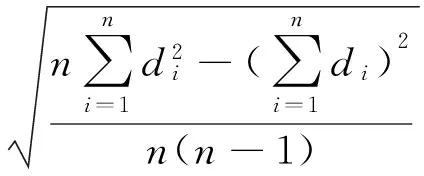
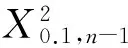
1.2.2 稳健统计方法

开源统计软件R是诞生于20世纪80年代的统计语言S的一个分支，而统计软件S-PLUS则是S的商业化版本，R和S-PLUS具有较好的兼容性，两者很多语言命令和程序包非常相似。与S-PLUS不同，R作为一款开源的统计软件，可供世界各地的统计学研究者根据工作需要使用其提供的数学计算环境开发各类统计程序包，并将其上传至CRAN等平台供其他R软件用户使用。因此，统计软件R日益受到各国统计学研究者的青睐。

用统计软件R和S-PLUS分别根据稳健四分位距(IQR，R软件)、绝对中位差(MAD，R软件)、Huber稳健估计(R软件MASS程序包)、Hubers稳健估计(R软件MASS程序包)[4-5]、Huber M估计(S-PLUS)和Bisquare M估计(S-PLUS)[6]构建4个浓度点的稳健中心值、稳健标准偏差。这6种方法为常用的稳健方法，基于这些稳健统计量重新计算变异系数、置信区间和预测区间，并与非稳健方法比较。

2 结果与讨论

2.1臭氧现场比对核查相对偏差/偏差数据分布情况

根据53台现场分析仪在臭氧现场比对核查中日常浓度点、100×10-9mol/mol和400×10-9mol/mol浓度点 的相对偏差及零点的偏差计算的基本统计量汇总见表1。通过核密度图和直方图(图1～图4，窗宽bw为density程序中默认的高斯核函数计算结果，分别为2.88%、1.64%、1.64%和0.56×10-9mol/mol)进一步观察各浓度点相对偏差/偏差的分布情况，发现4个浓度点比对结果在中心区域内大致呈现出正态分布的趋势，但是由于两侧极端值的出现，破坏了整体数据的正态分布趋势。通过对各个浓度点整体数据的正态性进行Shapiro-Wilk检验(表1)，发现各浓度点整体数据均不符合正态分布(P<0.05)。

表1 各浓度点相对偏差/偏差的统计量汇总

注：“*”表示零点偏差，单位为mol/mol。

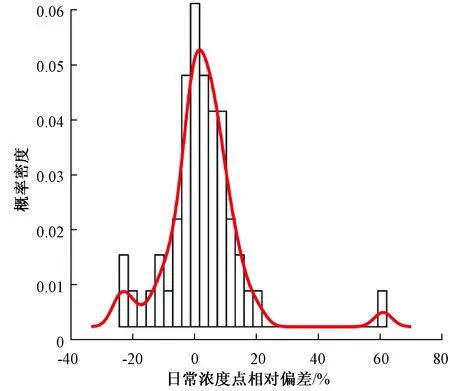
图1 日常浓度点相对偏差的核密度图与直方图叠加Fig.1 The density plots and histograms of the relative deviation of normal concentration point

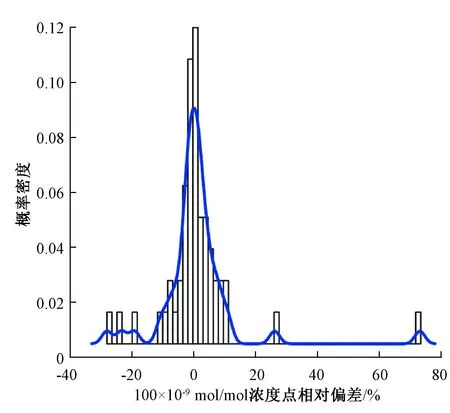
图2 100×10-9 mol/mol浓度点相对偏差的核密度图与直方图叠加Fig.2 The density plots and histograms of the relative deviation of 100×10-9 mol/mol concentration point

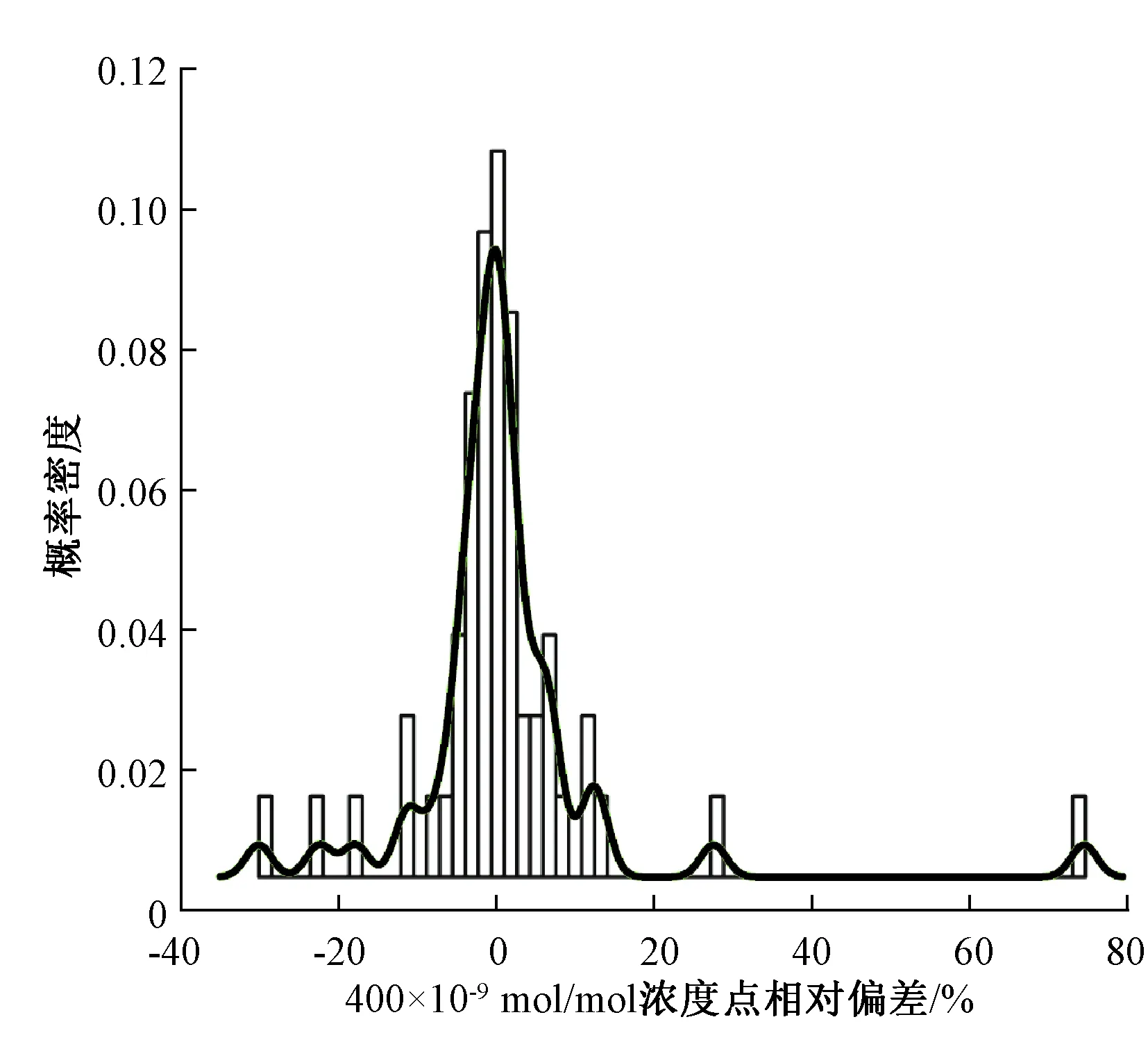
图3 400×10-9 mol/mol浓度点相对偏差的核密度图与直方图叠加Fig.3 The density plots and histograms of the relative deviation of 400×10-9 mol/mol concentration point

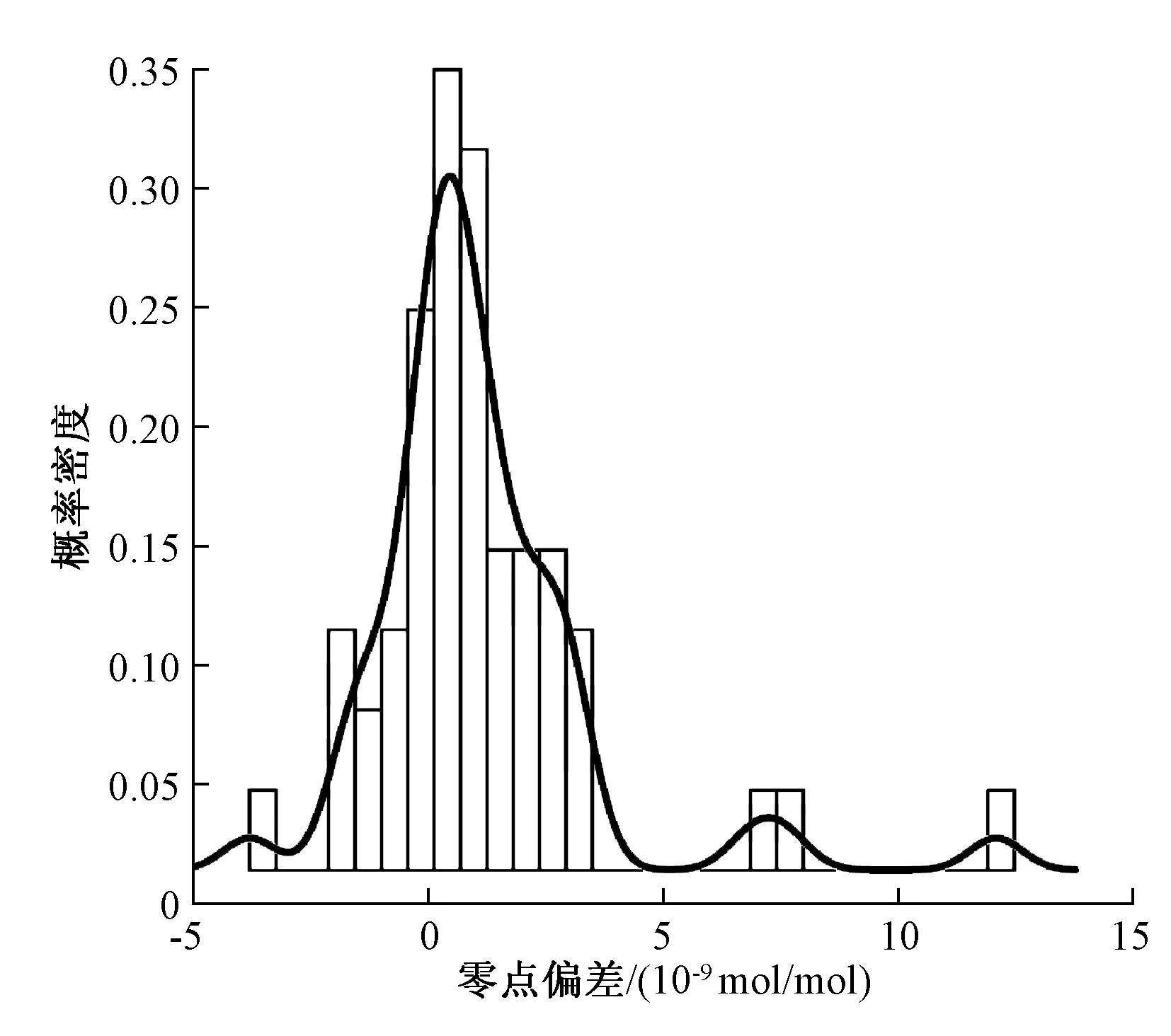
图4 零点偏差的核密度图与直方图叠加Fig.4 The density plots and histograms of the deviation of zero point

2.2臭氧现场比对核查数据稳健与非稳健统计结果比较

稳健统计可以在不剔除数据的前提下有效降低不符合实际分布的异常值对于正确估计总体统计量的破坏，其原理已广泛应用于实验室间比对等一系列环境监测质量管理工作中[7-10]。本研究采用6种常用稳健统计方法，分别对各浓度点相对偏差/偏差的中心值和标准偏差进行了稳健估计，并用稳健中心值和稳健标准偏差代替均值和一般标准偏差重新计算变异系数、置信区间和预测区间(表2～表5)。结果显示，使用稳健统计方法估计得到的各浓度点相对偏差/偏差的中心值均更接近0，标准偏差也明显小于稳健前，95%的置信区间上下界均更接近0，95%的预测区间明显窄于稳健前，变异系数也显著低于稳健前。

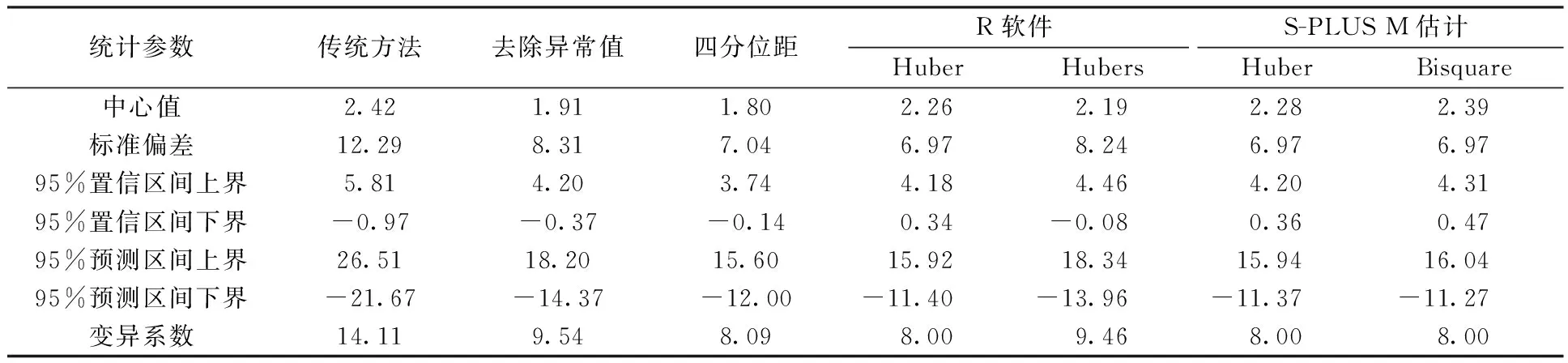
表2 日常浓度点相对偏差的稳健与非稳健置信区间、预测区间和变异系数

表3零点偏差的稳健与非稳健置信区间、预测区间和变异系数

Table3Therobustandnon-rubostconfidenceinterval,probabilityintervalandCVofzeropoint

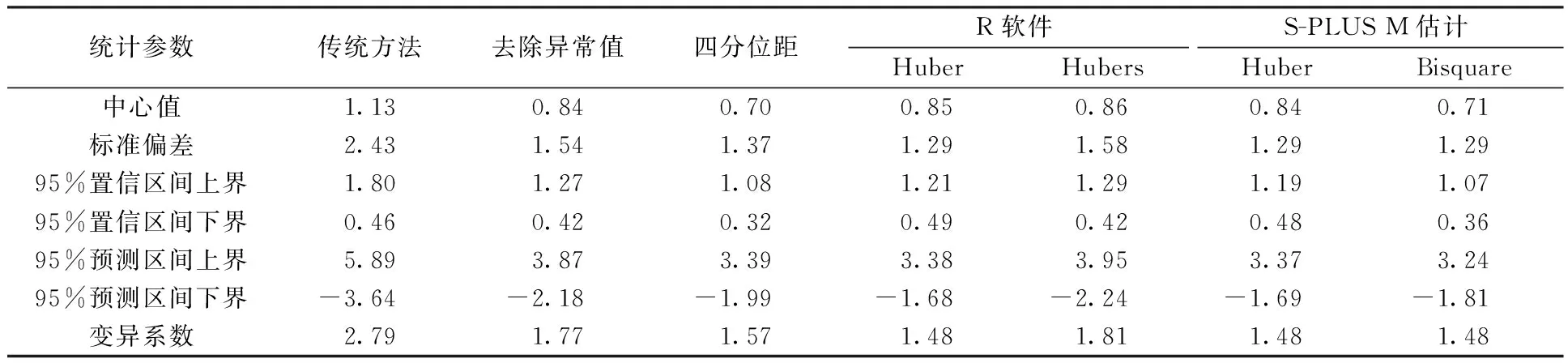
10-9 mol/mol

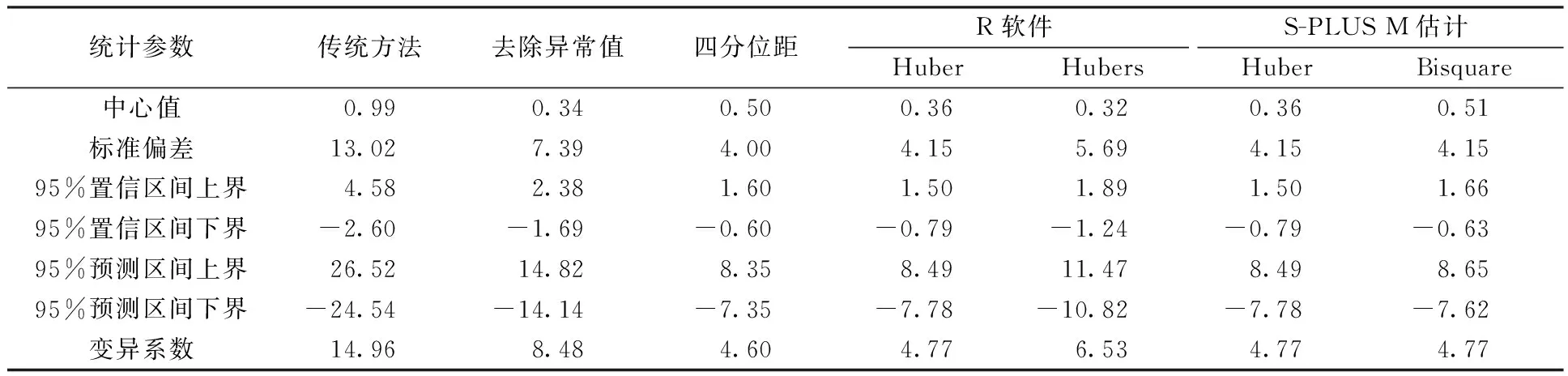
表4 100×10-9mol/mol相对偏差的稳健与非稳健置信区间、预测区间和变异系数

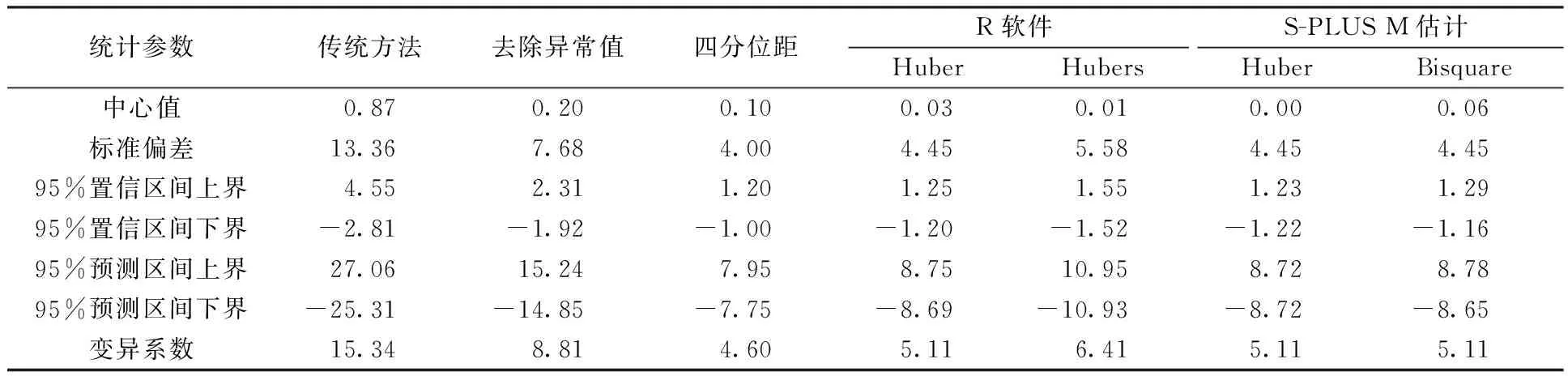
表5 100×10-9 mol/mol相对偏差的稳健与非稳健置信区间、预测区间和变异系数

为进一步探究稳健统计方法是否降低了两侧极端偏差造成的影响，我们采用国标中规定的Grubbs方法[3]剔除了数据集两侧的极端值(每侧1个)，使用剔除异常值后的数据重新按照传统方法计算相关统计量(表2～表5)。采用Grubbs方法剔除数据方法虽然能够减少异常值的影响，但其与稳健统计方法相比，该法只能剔除1～2个异常数据值，当数据量较大、异常值较多时无法有效降低所有异常值的影响，且剔除异常值的方法完全忽略了异常值包含的信息，较为极端，容易引起争议。本研究中通过比较剔除异常值前后统计量的变化可以反应异常值的影响；通过其与稳健统计结果的比较可以反映出稳健统计方法是否在一定程度上降低了异常值的影响。

比较结果后发现：剔除异常值后的各项统计量与剔除前相比变化明显，其中心值更接近0，而标准偏差也明显降低，稳健统计得到的结果与剔除异常值后的结果较为接近。这一结果表明，在臭氧现场比对核查结果评价过程中，稳健统计能够有效降低异常值对估计正确统计量的影响，相对偏差/偏差数据经过稳健统计后得到的置信区间与变异系数更贴近臭氧在线监测数据实际的偏倚和精密度。

在6种稳健统计方法中，IQR方法由于不需要迭代，计算较为简单，但对总体平均水平的度量效率并不高。除IQR方法外，另外几种稳健算法均为迭代算法，其中R软件的Huber算法与S-PLUS软件基于Huber函数的M-estimate计算方法基本一致，只在结束迭代的条件上稍有不同。S-PLUS软件基于Bisquare函数的M-estimate与Huber算法原理较为一致，均以MAD估计标准偏差，以中位值代替初始均值，不断迭代，构建稳健的平均值作为样本的平均值，但2种算法基于的函数并不相同，导致其迭代得到的稳健后平均数并不一致。与以上几种迭代方法只构建稳健平均值不同，Hubers方法是以中位数代替初始均值，通过MAD估计标准偏差，并进行多次迭代后使其逐渐收敛，通过不断迭代同时构建稳健的平均值和标准偏差，通过降低离群值的权重系数，提高了统计量的全局效率和耐抗性，研究表明该方法在数据离散程度相对高时较为温和可靠[9-11]，该方法的基本原理已被《Statistical methods for use in proficiency testing by interlabratory comparison》(ISO 13528—2015)、《测量方法与结果的准确度(正确度与精密度)》(GB/T 6379—2006)用于实验室间比对结果统计。在本研究的各个浓度点中，经Hubers稳健估计得到的标准偏差均最为接近剔除异常值后的标准偏差，且中心值也较为接近剔除异常值后的中心值，表明其在臭氧现场比对核查结果评价中较其他稳健统计算法温和。

2.32015年飞行检查臭氧现场比对核查结果

由表2可知，基于Hubers方法，2015年9个城市53台现场臭氧监测仪的日常浓度点相对偏差集中在-14.0%～18.3%(95%预测区间)， 95%置信区间为-0.08%～4.46%，其变异系数约为9.5%；100×10-9mol/mol浓度点相对偏差集中在-10.8%～11.5%(95%预测区间)， 95%置信区间为-1.24%～1.89%，其变异系数约为6.5%；400×10-9mol/mol浓度点相对偏差集中在-10.9%～11.0%(95%预测区间)，95%置信区间为-1.52%～1.55%，其变异系数约为6.4%；零点偏差集中在-2.2～4.0×10-9mol/mol(95%预测区间)，95%置信区间为-0.42～1.29×10-9mol/mol，其变异系数约为1.8×10-9mol/mol。

通过比较置信区间和变异系数，100×10-9mol/mol和400×10-9mol/mol浓度点臭氧在线监测数据的偏倚和精密度相似，日常浓度点在线监测数据的偏倚和精密度相比100×10-9mol/mol和400×10-9mol/mol浓度点较差。特别是日常浓度点稳健后的变异系数约为9.5%，表明国控网臭氧自动监测的数据质量仍有提升空间[12]。

结合各浓度点95%预测区间估计结果，建议：①未来臭氧现场比对核查零点偏差绝对值的合格标准可考虑在原有的基础上(5×10-9mol/mol)进一步收紧；②由于日常浓度点95%预测区间为-14.0%～18.3%，建议其相对偏差绝对值的合格标准继续保持原有的合格标准(15%)，以促进国控网臭氧自动监测数据质量的持续改进；③考虑到100×10-9mol/mol和400×10-9mol/mol浓度点95%预测区间分别为-10.8%～11.5%和-10.9%～11.0%，建议在原来15%的合格标准基础上，进一步将该浓度点相对偏差绝对值的合格标准收紧至12%以下。

2.4对我国臭氧自动监测质控工作的建议

在包括臭氧在内的气态污染物(SO2、NO2、CO)自动监测质控工作中，美国环保局要求各运维单位需进行2周1次的单点质控检查，并通过第2.2.1节介绍的传统统计方法评价其年度监测数据的精密性与准确性。鉴于此，建议我国运维单位在对现场包括臭氧在内的气态污染物分析仪进行周期性的零跨校准之前对其进行单点质控检查，并记录单点检查的相对偏差[13]。经过一段时间的数据积累后，管理单位可汇总周期内某点位各次单点核查的相对偏差，通过估算该点位气态污染物在线监测数据的变异系数或置信区间，以评价该点位监测数据的精密性和准确性。通过汇总周期内区域内各个点位的数据，可评价周期内该区域臭氧监测数据的精密性和准确性，并通过计算预测区间查找问题设备，以采取相应措施以推动区域数据质量的持续改进。

3 结论

与传统统计方法相比，稳健统计在不剔除数据的情况下能够更为准确地评价一定周期内臭氧自动监测数据的精密性和准确性。其中Hubers方法相对其他稳健统计方法较为温和，更适用于臭氧现场比对核查结果的统计。通过稳健统计方法处理臭氧现场比对核查数据，汇总计算各台现场分析仪偏差/相对偏差的变异系数、置信区间和预测区间，能够评价固定周期内我国臭氧监测数据的准确性和精密性，帮助我国制定臭氧现场比对核查的合格标准，为我国臭氧监测数据质量的评价和持续改进提供依据。

[1] 鲍蕾, 刘萍, 翟崇治, 等. 紫外光度法臭氧自动监测仪及其标准传递方法[J]. 中国环境监测, 2015, 31(1): 128-133.

BAO Lei, LIU Ping, ZHAI Congzhi, et al. Ozone automatic monitors based on ultraviolet spectrophotometry and relevant standard transfer methods[J]. Environmental Monitoring of China, 2015, 31(1): 128-133.

[2] US. Government Publishing Office. 40 Code of Federal Regulation Part 58 App A Sec 4.1: CFR 40-58-App. A: 2014 [S/OL]. [2014-07-01]. https://www.gpo.gov/fdsys/pkg/CFR-2014-title40-vol6/pdf/CFR-2014-title40-vol6-part58-appA.pdf.

[3] GRUBBS F E. Sample criteria for testing outlying observations [J]. Annals of Mathematical Statistics, 1950, 21(1): 27-58.

[4] HUBER P J. Robust Statistics [M]. Hoboken, New Jersey: John Wiley & Sons Inc, 1981.

[5] VEMABLES W N, RIPLEY B D. Modern Applied Statistics with S, Fourth edition [M]. Springer: Berlin-Heidelberg, 2002.

[6] MARONNA R A, MARTIN R D, YOHAI V J. Robust Statistics: Theory and Methods [M]. Hoboken, New Jersey: John Wiley & Sons, Inc, 2006.

[7] 滕曼, 付强, 杨婧, 等. 2011年全国环境监测实验室地表水挥发性有机物检测能力分析[J]. 环境影响与健康，2013, 30(12): 1 108-1 109.

TENG Man, FU Qiang, YANG Jing, et al. Results analysis of proficiency assessment of VOCs monitoring in water [J]. Journal of Environment and Health, 2013, 30(12): 1 108-1 109.

[8] 滕曼, 付强, 吴晓凤, 等. 环境监测实验室水中砷、汞监测能力考核结果评价. 中国环境监测，2014，30(4)：183-187.

TENG Man, FU Qiang, WU Xiaofeng, et al. Results analysis of proficiency assessment of As and Hg monitoring in ground water [J]. Environmental Monitoring in China, 2014, 30(4): 183-187.

[9] 刑小茹, 马小爽, 田文, 等. 实验室间比对能力验证中的两种稳健统计技术探讨. 中国环境监测，2011, 27(4)：4-8.

XING Xiaoru, MA Xiaoshuang, TIAN Wen, et al. Two robust statistic techniques in proficiency testing by interlaboratory comparisons [J]. Environmental Monitoring in China, 2011, 27(4): 4-8.

[10] 吴忠祥. 实验室能力验证中的分割水平检测样品与稳健统计技术[J]. 中国环境监测, 2003, 19(4): 8-10.

WU Zhongxiang. Split-level test sample and robust statistics techniques in laboratory proficiency testing [J]. Environmental Monitoring in China, 2003, 19(4): 8-10.

[11] 郭亚帆. 稳健统计以及几种统计量的稳健性比较分析 [J]. 统计研究, 2007, 24(9): 82-85.

GUO Yafan. Robust statistic and comparative analysis of the robustness of the statistics [J]. Statistical Research, 2007, 24(9): 82-85.

[12] US. Environmental Protection Agency. Quality Assurance Handbook for Air Pollution Measurement Systmes, Volume Ⅱ: USEPA 454/B-13-003: 2013 [S/OL]. [2013-05-01]. https://www3.epa.gov/ttnamti1/files/ambient/pm25/qa/QA-Handbook-Vol-II.pdf.

[13] 师耀龙, 滕曼, 姚雅伟, 等. 美国环境空气臭氧量值传递的经验与启示[J]. 中国环境监测, 2016, 32(4): 29-34.

SHI Yaolong, TENG Man, YAO Yawei, et al. Experience and illumination of ambient air ozone standard transfer in the United States [J]. Environmental Monitoring of China, 2016, 32(4): 29-34.

TheApplicationofRobustStatisticsinAnalyzingDatafromtheLocalEvaluationofAmbientAirOzoneOnlineMonitoring

SHI Yaolong1, YANG Jing1, YAO Yawei1, LI Cheng2, TENG Man1, CHAI Wenxuan1, CHU Baolin1, FU Qiang1

1.State Environmental Protection Key Laboratory of Quality Control in Environmental Monitoring, China National Environmental Monitoring Centre, Bejing 100012, China 2.Institute of Science and Technology, Agricultural University of Hebei, Baoding 071001, China

Based on the data from local evaluations of 53 ambient air ozone analyzers in 9 cities, the application of robust and normal statistics in evaluating the accuracy and precision of the ozone monitoring data from national ambient air monitoring network were compared. The results indicated that robust statistics could reduce the impact of outliers to evaluate the data quality of online ozone monitoring, fitting with the local evaluation data; based on the Hubers robust method, the 95% confidence interval of normal ozone concentration is between -0.1% and 4.5% in 2015, the 95% prediction interval is between -14.0% and 18.3%, the coefficient of variation is 9.5%. The data quality of ozone monitoring still need to be improved.

ambient air monitoring; ozone; local evaluation; robust statistics

X84

：A

：1002-6002(2017)04- 0207- 06

10.19316/j.issn.1002-6002.2017.04.26

2016-05-27;

：2016-08-25

师耀龙(1988-)，男，河北保定人，博士，工程师。

楚宝临