复杂网络视角下的港口连通性建模及应用

潘静静，王晓峰

1)上海海事大学信息工程学院，上海 201306；2)福建农林大学交通与土木工程学院，福建福州 350108

【交通物流/TransportationLogisitcs】

复杂网络视角下的港口连通性建模及应用

潘静静1,2，王晓峰1

1)上海海事大学信息工程学院，上海 201306；2)福建农林大学交通与土木工程学院，福建福州 350108

为评价港口的连通性，选取6个复杂网络拓扑特征作为港口连通性的评价指标，利用主成分方法构建港口连通性评价模型．通过搜集6家国际运力排名靠前的班轮公司船期数据，建立真实的航运网络，以验证模型的可行性和有效性，并用于海上丝绸之路战略背景下的福建省港口连通性分析．结果表明，厦门港的连通性最强，福州港次之，泉州港的连通性最弱；评价指标中，度中心性、特征向量中心性和平均路径长度对港口连通性影响较大．根据评价结果，提出福建省港口发展的定位和对策．

交通运输系统工程；港口连通性；复杂网络；主成分分析；航运网络；海上丝绸之路

港口为货物提供装卸和转运服务，是海上运输网络的重要节点．承运人在港口节点布局和航线设计时，通常会考虑港口的连通性，即港口与其他港口之间实现货物流通的便捷程度．一般说来，港口的连通性越强，在港口之间找到一条最短路径的可能性越大，货物在港口之间流通的成本也越低，意味着越能够吸引货主和船公司，从而为港口带来更多的货物[1]．建模和测算港口连通性，明确港口在特定区域乃至全球范围的地位，对港口在激烈竞争环境中的定位与建设有重要现实意义．

连通性分析在航空和公路领域应用较多．大部分研究通过评价连通性，量化并评估航空和公路网络的可靠性和交通运输服务水平[2]．在航运领域，早期研究主要关注港口的可达性，Cullinane等[3]认为集装箱港口的可达性意味着集装箱货物在港口之间流通的潜在性，李振福等[4]将海运网络中两港之间所有路线中最短路线作为衡量可达性的标准．然而，货物流通还受班轮服务能力及港口转运能力等现实条件制约，港口之间可达不等同港口之间实际连通．因此，近年来更多学者转向研究港口连通性，这些研究从连通性评价指标选取角度可分为两类．一类指标基于港口自身信息，如Hoffmann[5]考虑海上运输中船队配置、集装箱运力、班轮公司数量、航线数量和最大船舶规模5个因素，创建了一个162个沿海国家的班轮运输连通性指数；Tang等[6]将起讫港口的数量作为港口连通性评价的依据；Lam等[7]使用运输能力、贸易线路、地理位置和班轮航线评价港口之间的连通性．另一类连通性评价指标基于全球航运网络视角，如Tovar等[8]设计了航运网络及港口节点相关的两组指标对港口之间的连通性进行评价；Jiang等[9]从运输时间和能力角度建立港口转运能力评价模型用以衡量港口连通性，并分析了港口连通性对航运网络的影响；Wang等[10]使用TOPSIS(technique for order preference by similarity to an ideal solution)方法对渤海湾内的青岛港、大连港和天津港进行连通性评价．从上可见，基于全球航运网络视角分析港口连通性是研究的趋势，而该视角下对我国特定港口连通性的研究尚不多见．复杂网络是研究网络的一种主要工具[11]．研究表明，航运网络具有小世界和无标度特性，论证了航运网络是复杂网络[12-14]．

本研究借助复杂网络分析港口的连通性，选取6个复杂网络拓扑特征作为港口连通性的评价指标，利用主成分方法构建港口连通性综合评价模型，以期解决多指标评价结果所体现的港口连通性内涵重叠这一局限性．为验证港口连通性评价模型的可行性和有效性，通过搜集班轮公司的船期数据建立真实的航运网络，使用所构建的模型解析福建省港口在全球航运网络中的复杂连通性，以期为福建省港口规划以及融入海上丝绸之路建设提供决策参考．

1 港口连通性建模

1.1港口连通性评价指标选取

港口连通可理解为从某个港口出发，至少可找到1条路径将货物运往其他港口．本研究将港口连通性界定为港口与其他港口之间实现货物流通的便捷程度．借鉴Tovar等[8]评价指标选取思路，从港口在航运网络中的相对重要性及其对航运网络连通影响程度两方面对港口连通性进行分析．选取复杂网络的中心性作为衡量节点的相对重要性指标，包括度中心性、介数中心性和特征向量中心性，选取复杂网络的核数、聚类系数和平均路径长度作为衡量节点对网络连通影响程度的指标．

1.1.1度中心性

度是网络中与该节点直接相连的其他节点的数量，港口的度中心性越大说明有越多的港口与该港口直接相连，该港口在网络中越重要，定义为[15]

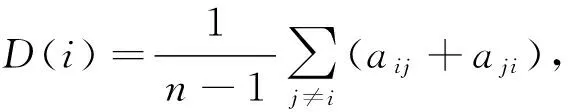
(1)

其中，N为航运网络中港口的集合；n=|N|为港口数量；aij为邻接矩阵A的元素，若两个连续的港口i和j之间至少有一条航线经过时aij=1， 否则为0．

1.1.2介数中心性

介数中心性指任意两个节点的最短路径通过特定节点的数量，如式(2)[15]．介数中心性越大表明经过该港口的网络流越多，该港口在网络中越重要．

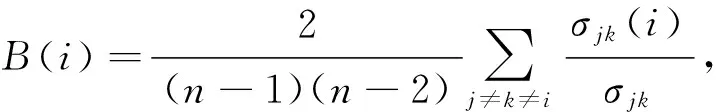
(2)

其中，σjk是港口j到k的所有最短路径的数量；σjk(i)是港口j到港口k的最短路径中经过港口i的数量．

1.1.3特征向量中心性

特征向量中心性是度量某节点的邻居节点的重要性，其值越大意味着与该港口直接相连的港口在网络中越重要．将邻接矩阵最大特征值对应的特征向量作为网络中节点的分值，节点i对其他节点分值的贡献即为特征向量中心性[15]，即

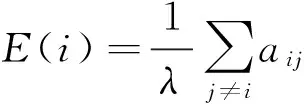
(3)

其中，λ为A的最大特征值；vj为节点的中心性分值，即λ对应的特征向量．

1.1.4核 数

网络的k-核指反复去掉度值小于k的节点及其连线后所剩的子网络，若一个节点存在于k-核， 而在(k+1)-核中被移去， 则该节点的核数为k， 记为H(i)=k[15]． 节点的核数表明节点在核中的深度，高核节点连通性高，去除这些港口后对整个航运网络的连通性影响也越大．

1.1.5聚类系数

聚类系数表示网络中某节点的邻居节点也相邻的概率，聚类系数越大表明与该港口直接相连的港口之间有航线相连的概率越大，即该港口对航运网络连通的影响也越大，定义为节点i的邻居节点之间实际存在的边数占可能的最大连接边数的比例为[15]

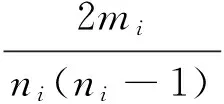
(4)

其中，ni是与节点i相邻的节点数量；mi是ni个节点相连的实际边数，若这ni个节点都相互连接，它们之间最多存在ni(ni-1)/2条边．

1.1.6平均路径长度

平均路径长度是连接两个港口的最短路径上的边数，其值越小说明该港口的货物越易到达其他港口，该港口对航运网络连通的影响也越大．节点i的平均路径长度定义为节点和网络中其他节点之间最短路径所经过的边数的平均值[15]，即

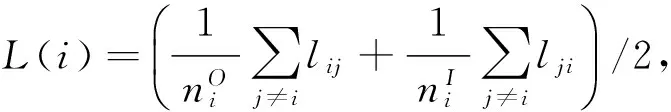
(5)

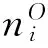
1.2港口连通性评价模型构建

由于选取的6个指标之间存在一定的相关性，反映出港口连通性内涵存在一定程度的重叠，同时，为增强连通性评价结果的易理解性，直观看出港口在航运网络中的连通性地位，应用主成分分析法约简评价指标，并使用主成分指标构建连通性综合评价函数[16]．

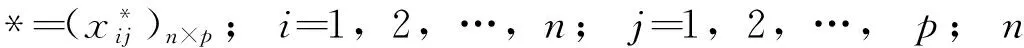
2 福建省港口连通性评价

2.1研究对象及数据来源

福建省在“一带一路”战略中定位为21世纪海上丝绸之路建设的核心区，福建沿海的福州港、厦门港和泉州港也成为海上丝绸之路重点建设港口.因此本研究将这3个港口作为研究对象．

建立数学模型评价港口连通性，首先需搜集航线数据．在全球航运中，超过70%的货物以集装箱方式通过班轮运输完成[17]．因此，搜集Alphaliner统计的运力排名靠前的6家班轮公司公布在各自官网的2015年第4季度船期数据[18]．这6家公司分别是马士基、达飞、中远海运、赫伯罗特、长荣和韩进海运，它们总的集装箱运输市场份额约占全球班轮公司的40.3%，航线网络遍布6大洲，其船期数据基本可反映全球的航运状况．其次，确定航运网络的边界．根据中国在2015年发布的《推动共建丝绸之路经济带和21世纪海上丝绸之路的愿景与行动》文件定义，将亚洲港口、欧洲港口和大洋洲港口作为海上丝绸之路港口，删除所有包含非海上丝绸之路港口的航线，整理得到涉及572个海上丝绸之路港口的2299条海上丝绸之路航线．最后，利用航线数据构建航运网络，以邻接矩阵形式表达．航线是船舶在起讫港口之间航行的线路，包含船舶挂靠港口的次序，通过MatlabR2016a软件处理航线数据的步骤如下：对港口进行编号，初始化行和列值为572的邻接矩阵，若两个连续的港口之间至少有1条航线经过，则两个港口对应的邻接矩阵元素值为1，否则为0．

2.2福建省港口连通性评价结果

计算572个港口在6个连通性指标上的评价结果，结果见图1．其中，福建省各港口在6个连通性指标上的评价结果见表1．

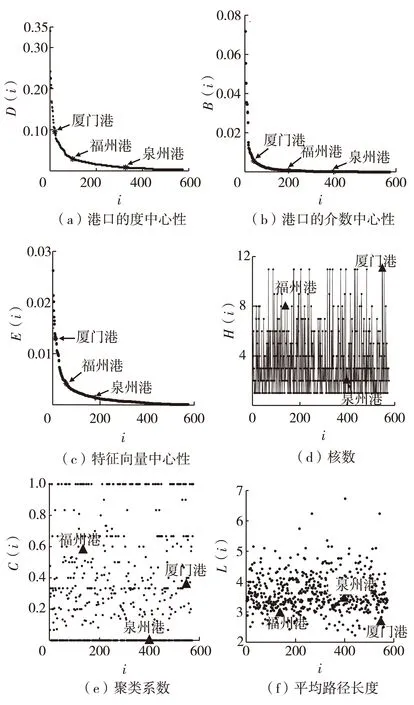
图1 572个港口的连通性评价结果Fig.1 Connectivity evaluation results of 572 ports

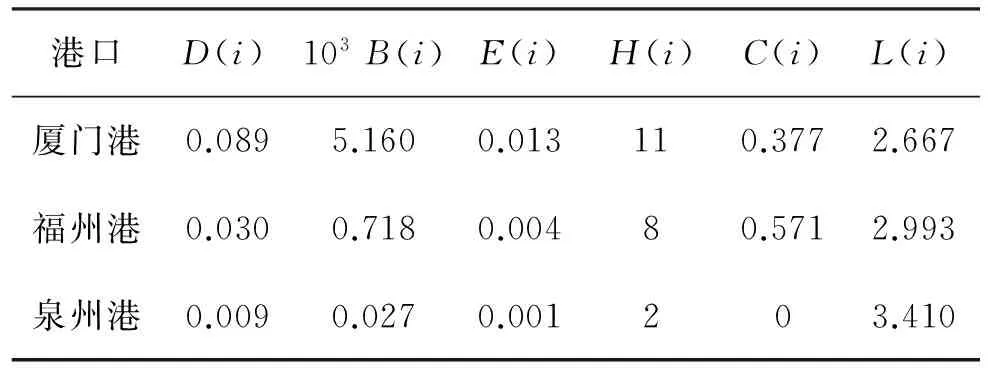
港口D(i)103B(i)E(i)H(i)C(i)L(i)厦门港0.0895.1600.013110.3772.667福州港0.0300.7180.00480.5712.993泉州港0.0090.0270.001203.410

从表1可见，厦门港的度中心性值最大，说明与福州港、泉州港相比，与厦门港直接相连的海上丝绸之路港口数量最多；厦门港的介数中心性远超过福州港和泉州港，意味着有最多的班轮航线在厦门港挂靠；厦门港的特征向量中心性值最大，说明与厦门港直接相连的港口在航运网络中占更重要的地位；厦门港的核数最大，表明厦门港在航运网络中属于核心港口；福州港的聚类系数小于厦门港，意味着度值小的港口更趋于聚集成团，而泉州港聚类系数为0，这是由于与泉州港相邻的港口之间没有直达航线；从平均路径长度结果看，世界上任意一个港口与厦门港、福州港之间通过不到3个航段就可相互连通，和泉州港之间则需4个航段．

将所有港口的指标数据写入矩阵X*=xij;i=1, 2, …, 572;j=1, 2, …, 6. 对X*进行标准化处理得到样本矩阵X， 通过X计算指标间的相关性，得到60%指标的皮尔逊相关系数 |R|>0.5，说明6个指标之间存在较强的相关性．借助SPSS 24.0进行Bartlett球形度和KMO检验，结果显示：巴特利球形度近似卡方值为3 505.83，统计量为15，相应概率为0；KMO测度值为0.667，接近1.0．上述结果表明，本研究样本数据适合进行主成分分析，其结果如表2．

表2 主成分分析结果

为使综合评价分析最大程度地减少信息损失，提取累计方差贡献率为92.13%的前3个主成分fi1、fi2和fi3， 构造港口连通性评价函数如式(6)，并通过该函数计算每个港口的连通度，结果如图2．

Zi=0.631 0fi1+0.198 5fi2+0.092 6fi3

(6)

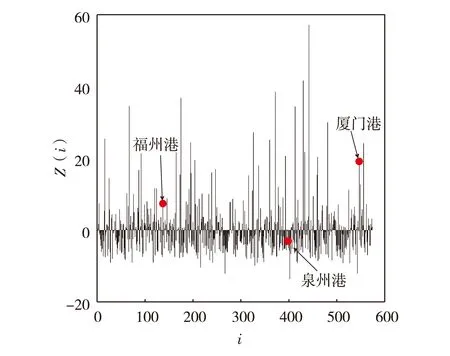
图2 海上丝绸之路港口连通度Fig.2 (Color online) Connectivity of ports along Maritime Silk Road

从连通度计算结果看，厦门港、福州港和泉州港的连通度分别为18.53、7.462和-2.994，在572个港口中排名分别为第18、第52和第357．为直观分析港口的连通性地位，按连通度大小将样本港口分为4个级别：Ⅰ级强连通型港口(15≤Zi<50)， Ⅱ级较强连通型港口(5≤Zi<15)， Ⅲ级一般连通型港口(0≤Zi<5)， Ⅳ级弱连通型港口(Zi<0)． 根据上述分类，得到Ⅰ级港口25个，占比4.37%；Ⅱ级港口56个，占比9.79%；Ⅲ级港口165个，占比28.85%；Ⅳ级港口326个，占比56.99%．显然，厦门港为Ⅰ级港口，福州港为Ⅱ级港口，泉州港为Ⅳ级港口．

2.3福建省港口连通性地位

为深入分析福建省港口连通性的现状和地位，选取“一带一路”重点建设的8个世界百强港口进行比较，分别是：上海、深圳、宁波-舟山、广州、青岛、天津、大连和烟台．绘制11个港口吞吐量与连通度散点图(图3)．其中，TEU为国际标准箱单位．

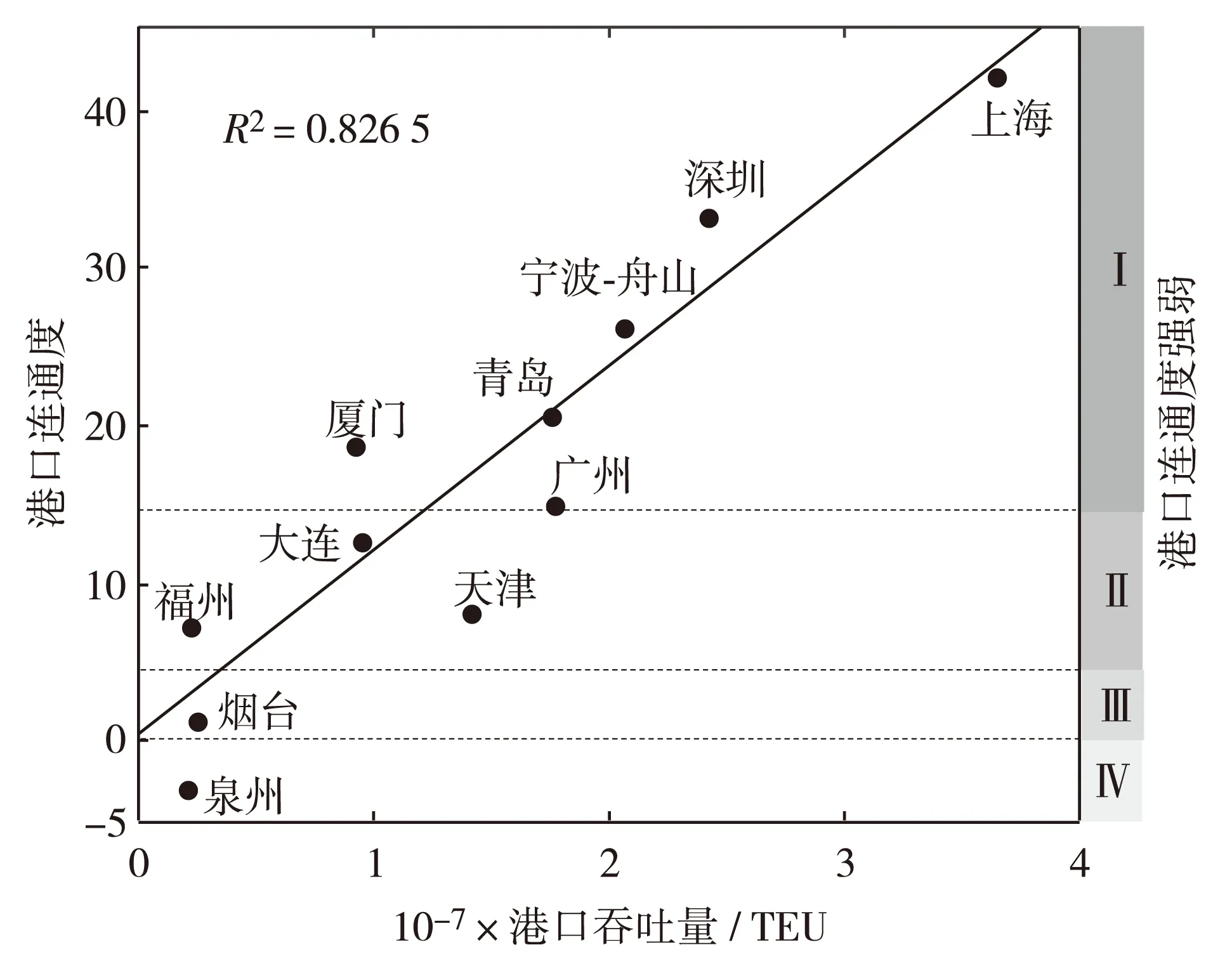
图3 港口吞吐量与连通度相关性分析Fig.3 Correlation analysis between the ports throughput and connectivity

图3表明，港口的连通度排名与其吞吐量排名大体一致，在一定程度上验证了本研究连通度评价方法的有效性与可行性．港口连通度与吞吐量的线性拟合结果表明，二者存在显著正相关，可决系数R2=0.8635． 在Ⅰ级强连通型港口中，上海港的连通度排名和吞吐量排名均位于第1，且远高于其他港口．上海被定位为“国际性综合交通枢纽”，近年来上海港的基础设施能力提升很快，是我国航线密度最大的港口．大部分Ⅰ级港口，如深圳、宁波—舟山和青岛，都具有较为一致的连通度和吞吐量排序，除了广州港和厦门港．广州港的吞吐量排名第4，但连通度排名仅为第6，这可能是由于广州与周边大型港口(如深圳和香港)地理位置接近，在提供转运服务时容易被邻近港口替代．厦门港的吞吐量排名第8，而连通度排名第5，这与其优越的地理位置有关．厦门港是连接两岸三地和亚太地区集装箱运输的干线港，作为我国东南沿海的枢纽港口，在沿海货物转运中发挥着重要作用．在Ⅱ级较强连通型港口中，大连港和福州港的连通度与吞吐量保持了一致的水平.值得一提的是天津港，从图4可见，天津港座落在偏离拟合直线较多的位置，其连通度排名弱于吞吐量排名，这意味着天津港的国际中转运业务较少，这与其地理位置有很大关系，天津港位于渤海湾底部，海上交通远不及周边大连港和青岛港便利．烟台和泉州是Ⅲ级和Ⅳ级港口，是海上丝绸之路重点建设港口中吞吐量和连通度最弱的港口．

标准化11个港口的连通性评价指标D(i)、B(i)、E(i)、H(i)、C(i)和L(i)数据，按照港口连通度强弱自左向右排序后绘制出图4，分析6个指标对港口连通度的影响．

从图4可见，随着港口连通度的不断减弱，D(i)、B(i)、E(i)和H(i)数值不断下降，C(i)和L(i)不断增加．这说明，港口的度值、介数、特征向量和连通度呈正相关，港口的聚类系数和平均路径长度和连通度呈负相关．进一步计算上述指标与连通度Z(i)的皮尔逊相关系数分别为0.962、0.781、0.906、0.644、-0.689和-0.896．结果表明，度中心性、特征向量中心性和平均路径长度对连通度的影响远大于介数中心性、核数和聚类系数．也就是说，提升度中心性、特征向量中心性和平均路径长度将有助于大幅提升港口的连通性．可见，港口应通过提升物流服务水平，吸引班轮公司挂靠，增加出入度值，提升港口的度中心性，尤其是开辟与连通性较强的港口间的航线，从而提升港口的特征向量中心性，缩短港口之间平均路径长度．

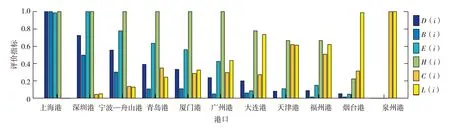
图4 “一带一路”重点建设港口的连通性评价结果Fig.4 (Color online) Connectivity evaluation results of the key construction ports of the Belt and Road

3 结 论

本研究采用复杂网络和主成分分析法对港口连通性进行建模，并用于福建省港口连通性的评价，结果表明：

1)厦门港为Ⅰ级强连通型港口，连通度排名位于海上丝绸之路网络第18，在世界港口吞吐量中排名第16，与连通度排名靠前的强连通型港口，如新加坡、上海、巴生、香港、釜山、鹿特丹、深圳、丹戎帕拉帕斯、宁波-舟山、阿尔赫西拉斯、杰贝阿里、比雷埃夫斯、科伦坡、汉堡、青岛、高雄和苏伊士相比，厦门港的国际中转业务有待拓展．建议厦门港重点发展国际集装箱干线运输，通过优惠政策支持吸引海上丝绸之路沿线国家和地区，尤其是东南亚、台湾等地的中转货物流向厦门港，提升国际班轮航线的密集度；进一步改善通关效率，提高港口服务能力，打造成东南沿海国际中转枢纽港．

2)福州港为Ⅱ级较强连通型港口，在海上丝绸之路航运网络中，其连通度排名第52，在世界港口吞吐量中的排名第75，说明福州港在整个网络中的港口链接能力较强、海向腹地吸引力大于陆向腹地．建议福州港积极开拓陆向腹地，吸引周边地区和更为宽广的内陆腹地货物，通过出台优惠政策，加强与内陆无水港和飞地港的合作，大力发展临港工业，延伸港口经济产业链；完善福州港集疏运体系，建设陆向腹地货物从福州港进出的公路和铁路运输通道，打造为福建省连通海上丝绸之路沿线港口的福建省枢纽港．

3)泉州港为Ⅳ级弱连通型港口，在海上丝绸之路航运网络中，连通度排名第357，在国际物流网络中的影响力较小．与此同时，泉州港在世界港口吞吐量中排名第77，这主要源于泉州港本地货物生成量巨大，其内贸集装箱业务在全国排名第5．建议集中泉州港码头资源，提升码头专业化程度、港口生产效率和利用率，在继续发展临港产业和重点拓展大宗散货运输的基础上，开辟更多集装箱内支线，打造为福州港和厦门港的远洋喂给港．

/

：

[1] Wilmsmeier G, Hoffmann J, Sanchez R J. The impact of port characteristics on international maritime transport costs[J]. Research in Transportation Economics,2006,16(1):117-140.

[2] Reggiani A, Nijkamp P, Lanzi D. Transport resilience and vulnerability: the role of connectivity[J]. Transportation Research Part A: Policy and Practice,2015,81:4-15.

[3] Cullinane K, Wang Yuhong. A capacity-based measure of container port accessibility[J]. International Journal of Logistics Research and Applications,2009,12(2):103-117.

[4] 李振福，李 贺，徐梦俏，等．世界海运网络可达性对比研究[J]．大连海事大学学报，2014，40(1)：101-104． Li Zhenfu, Li He, Xu Mengqiao, et al. Comparison research on reachability of the global shipping network[J]. Journal of Dalian Maritime University,2014,40(1):101-104.(in Chinese)

[5] Hoffmann J. Liner shipping connectivity[J]. UNCTAD Transport Newsletter,2005,27(1):4-12.

[6] Tang L C, Low J M W, Lam S W. Understanding port choice behavior: a network perspective[J]. Networks and Spatial Economics,2011,11(1):65-82.

[7] Lam J S L, Wei Y Y. Dynamics of liner shipping network and port connectivity in supply chain systems: analysis on East Asia[J]. Journal of Transport Geography,2011,19(6):1272-1281.

[8] Tovar B, Hernández R, Rodríguez-Déniz H. Container port competitiveness and connectivity: the Canary Islands main ports case[J]. Transport Policy,2015,38(C):40-51.

[9] Jiang Jianlin, Lee L H, Chew E P, et al. Port connectivity study: An analysis framework from a global container liner shipping network perspective[J]. Transportation Research Part E: Logistics and Transportation Review,2015,73:47-64.

[10] Wang G W Y, Zeng Qingcheng, Li K, et al. Port connectivity in a logistic network: the case of Bohai Bay, China[J]. Transportation Research Part E: Logistics and Transportation Review,2016,95:341-354.

[11] 李 娜，丰建文，赵 毅．具有马氏跳拓扑复杂网络的有限时间同步[J]．深圳大学学报理工版，2016，33(4) :359-366． Li Na, Feng Jianwen, Zhao Yi． Finite-time synchronization of Markovian jump complex networks[J]．Journal of Shenzhen University Science and Engineering,2016,33(4):359-366．(in Chinese)

[12] 田 炜，邓贵仕，武佩剑，等．世界航运网络复杂性分析[J]．大连理工大学学报，2007，47(4)：605-609． Tian Wei, Deng Guishi, Wu Peijian, et al. Analysis of complexity in global shipping network[J]. Journal of Dalian University of Technology,2007,47(4):605-609.(in Chinese)

[13] Hu Yihong, Zhu Daoli. Empirical analysis of the worldwide maritime transportation network[J]. Physica A: Statistical Mechanics and its Applications,2009,388(10):2061-2071.

[14] Ducruet C, Zaidi F. Maritime constellations: a complex network approach to shipping and ports[J]. Maritime Policy & Management,2012,39(2):151-168.

[15] 孙玺菁，司守奎．复杂网络算法与应用[M]．北京：国防工业出版社，2015． Sun Xijing, Si Shoukui. Complex network algorithms and applications[M]. Beijing: National Defense Industry Press,2015.(in Chinese)

[16] 李序颖．应用统计分析方法[M]．上海：上海浦江教育出版社，2012． Li Xuying. Applied statistical analysis method[M]. Shanghai: Shanghai Pujiang Education Press,2012.(in Chinese)

[17] Wang Tingsong, Meng Qiang, Wang Shuaian, et al. Risk management in liner ship fleet deployment: a joint chance constrained programming model[J]. Transportation Research Part E: Logistics and Transportation Review,2013,60(4):1-12.

[18] Alphaliner. Top100operated fleets[EB/OL]. (2017-02-15). http://www.alphaliner.com/top100/index.php

【中文责编：英子；英文责编：木南】

Portconnectivitymodelbasedoncomplexnetworkanditsapplication

PanJingjing1, 2andWangXiaofeng1

1)CollegeofInformationEngineering,ShanghaiMaritimeUniversity,Shanghai201306,P.R.China2)CollegeofTransportationandCivilEngineering,FujianAgricultureandForestryUniversity,Fuzhou350108,FujianProvince,P.R.China

In order to identify the port connectivity status, we select six complex network topological features as the port connectivity indicators and construct the port connectivity model based on the principal component analysis. By collecting and using the service schedule data for six shipping capacity top-ranking liner companies, we build a real shipping network for verifying the feasibility and effectiveness of the port connectivity model. The model is used in evaluating the connectivity of the Fujian ports in the context of the Maritime Silk Road Strategy. The results show that Xiamen port has the strongest connectivity among the three major ports in Fujian, followed by Fuzhou Port and Quanzhou Port. The degree centrality, eigenvector centrality, and the shortest path length have the significant impacts on port connectivity. We put forward several development strategies for ports in Fujian.

transport system engineering; port connectivity; complex network; principal component analysis; shipping network; Maritime Silk Road

2017-03-02；Accepted：2017-05-21

Professor Wang Xiaofeng．E-mail: xfwang58@163.com

F 551；U 691

：Adoi：10.3724/SP.J.1249.2017.05544

Foundation：National Natural Science Foundation of China(71471109)；Social Science Fund of Fujian Province(FJ2015C107)

：Pan Jingjing, Wang Xiaofeng. Port connectivity model based on complex network and its application[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(5): 544-550.(in Chinese)

国家自然科学基金资助项目(71471109)；福建省社科规划资助项目(FJ2015C107)

潘静静(1984—)，女，福建农林大学讲师．研究方向：物流与供应链管理、航运大数据分析．E-mail：jjpan@fafu.edu.cn

引文：潘静静，王晓峰．复杂网络视角下的港口连通性建模及应用[J]. 深圳大学学报理工版，2017，34(5)：544-550.