基于形态模式的时间序列相似性度量算法

王 瑞 贾瑞玉

(安徽大学计算机科学与技术学院 安徽 合肥 230601)

基于形态模式的时间序列相似性度量算法

王 瑞 贾瑞玉

(安徽大学计算机科学与技术学院 安徽 合肥 230601)

时间序列的特征表示与相似性度量是时间序列数据挖掘的重要基础。针对现有的序列表示方法难以具体反映序列的形态变化趋势，导致相似度量结果不精确的问题，提出一种新的基于形态模式的相似性度量算法。该算法在分段线性表示的基础上，根据序列在不同时段的斜率变化情况，划分序列的分段形态模式并用特殊的字符进行表示，把时间序列转换成字符串序列，利用最长公共子序列方法计算字符串序列的距离作为时间序列之间的距离。最后通过实验验证该方法的有效性。理论分析和实验证明该方法对数据点的值不敏感，能够减少噪声的干扰，而且具有较高的准确性。

时间序列 相似性 形态 模式 斜率 子序列

0 引 言

时间序列是按时间顺序排列的实数序列，广泛存在于我们的生活中，如股市指数、气象数据、销售额度等[1-3]。时间序列具有时间有序性、数据量巨大且持续增长等特点，对这类数据进行处理的难度较大，因此时间序列的相似性度量方式与聚类方法的研究成为时间序列数据挖掘的热点，吸引了越来越多研究者的关注[4]。经典的时间序列的相似性度量方法主要有欧氏距离[5]、动态弯曲距离法(DTW)[6]，以及符号距聚合近似方法[7-8]等。近几年也不断有新的相似性度量算法被提出，这些方法广泛应用于时间序列的聚类、相似性搜索、序列预测等工作。

在文献[9]中提出的基于EMD的K-means的聚类算法能有效提取序列的整体趋势，根据上升、下降和保持三种状态对序列进行分段，但是没有考虑每段的作用强度。在文献[10]中把序列映射为趋势符号序列，构成趋势树，根据趋势符号是否相同决定相似性，方法简单有效，但是趋势判定条件较为复杂。在文献[11]中提出的层次分段相似度量算法根据极值点对序列进行层次分段，然后计算动态弯曲距离，时间复杂度有所降低，但用于高维数据的聚类工作时，耗时相对较多。在文献[12]中提出的基于斜率表示的相似性度量方法，根据斜率偏离程度决定相似度，计算过程简单，具有对数据的平移不敏感的优点，但是没有区分序列的模式差异，当序列的模式不同时，可能会有误判的风险。在文献[13]中提出涨落模式的概念，将时间序列表示成由布尔值{-1,0,1}构成的涨落模式序列，消除了数据值对时间序列距离计算的影响。该方法对序列的振幅伸缩、漂移和线性漂移均不敏感，但是模式的划分不够细致，结果可能不够精确，而且在原始序列基础上直接划分涨落模式，容易受噪声影响。

本文针对已有算法在时间序列的相似性度量过程中的各种局限性，提出了基于形态模式的相似性度量方法。该方法在分段线性表示的基础上，根据斜率确定分段形态模式，通过形态模式序列保存序列的变化趋势，使用最长公共子序列方法计算序列的相似性。形态模式序列确定后，距离度量过程将不再受原始序列中数据元素值的影响，最长公共子序列方法对数据值不敏感，而且支持序列的伸缩和漂移。

1 相关工作

1.1 时间序列分段表示

设时间序列S=(,,…,,…,),j=1,2,…,n，n是序列长度，表示点j对应的数值和时间。时间序列的相似是基于形态的，考虑到不同时间序列度量单位不同，在相似性度量时，度量单位不统一会对结果有一定影响，因此在度量相似性之前，需要对时间序列进行归一化处理，把数据统一映射到[0,1]区间，方便后期的数据分析。数据统一过程如下：

(1)

min(y)、max(y)分别表示序列中数据的最大值和最小值，y*表示统一处理后的数据。

不同的序列其关键点所在位置不同，因此在计算相似度之前，需要在分段后取并集，进行等长处理，即进行时刻对等，保证进行相似性度量的不同序列具有相同的分段数。

1.2 时间序列的涨落模式

根据时间序列的形态变化可以将时间序列大致划分为上升、下降和保持三种状态。王钊等[13]基于序列的形态变化提出涨落模式的概念，将原始时间序列保存为由布尔数据构成的扩展布尔型时间序列。用{1，0，-1}为取值范围的布尔型时序数据保存原始序列的变化趋势，只关注原有时序数据的形态特征，而不考虑其数值大小。用1表示上升，0表示保持，-1表示下降，在后续的相似度计算中使用生成的布尔型时序数据进行相似性度量。

定义1涨落模式。对于原始时间序列S=(,,…,,…,)，其扩展布尔型时间序列为B=(b1,b2,…,bj,…,bn-1)，二者之间的对应关系如下：

(2)

布尔数据序列B记录了原始序列S的所有形态涨落趋势，因此B是S的涨落模式序列。使用涨落模式的意义在于既保留了数据形态变化趋势，又消除了序列的数值信息对基于形态的相似性度量产生的影响，并且这种方法对数据的平移和伸缩不敏感。

三元涨落模式虽然能够反映序列的大体趋势是上升或下降，但是不能描述上升或下降速度的快慢，即使同样是上升状态，也存在快速上升和缓慢上升的区别。而且涨落模式的基本思想是直接对原始序列求取模式序列，长度为n的时间序列，对应的模式序列为n-1，所有的点都参与模式的划分，噪声的影响不可忽略。

2 基于形态模式的相似度量算法

2.1 形态模式定义

为了能够更细致地反映数据的变化趋势，本文将序列的变化趋势分为七种情况：快速上升、匀速上升、缓慢上升、持平状态、缓慢下降、匀速下降、快速下降，并分别用{3，2，1，0，-1，-2，-3}表示对应趋势。序列的形态变化趋势如图1所示，其中横线表示时间轴，箭头方向代表序列的当前趋势。

图1 时间序列的形态模式

斜率是反映曲线变化快慢的变量，为了能准确刻画时间序列的形态模式，本文方法在序列分段表示的基础上，首先取得分段序列对应的斜率序列，然后根据每段的斜率值确定对应的形态模式。

定义2形态模式。已知分段斜率列Sk={k1,…,ki,…,km}，参考表1中分段斜率和形态模式之间的关系，形态模式序列P={p1,…,pi,…,pm}中，pi可根据对应的分段斜率值确定。

表1 分段斜率和形态模式之间的关系

若ki≥0且ki>1则当前分段和时间轴之间的夹角大于45度，此时序列处于快速上升状态，形态模式为3，若ki<0且ki>1，则序列在快速下降，形态模式为-3，其他形态模式可类比得到。

2.2 距离度量方法

形态模式序列是由-3到3之间的数字构成的特殊字符串，形态模式序列的相似性度量可以采用最长公共子序列方法。它的基本思想是对于两个不同的模式序列，首先求得二者之间的最长公共子序列，进而计算该子序列在整个模式序列之中所占的比重，作为序列之间的相似值。下面分别给出最长公共子序列定义和基于最长公共子序列的相似度定义。

最长公共子序列可以通过动态规划方法求得，递归求解公式如下：

(4)

S1(i)和S2(j)分别表示S1的第i个元素和S2的第j个元素，其中L(i,j)表示S1和S2的最长公共子序列长度。

如果不同序列之间存在最长公共子序列，那么时间序列的相似性可由最长公共子序列在原序列中的比值决定。根据定义3可以得出基于最长公共子序列的相似性计算公式：

(3)

式中ls表示最长公共子序列的长度，min(ls1,ls2)表示序列S1和S2中较短的序列长度。

2.3 基于形态模式的相似度量算法

基于分段形态模式的相似度量算法将时间序列数据分段后转化为七元形态模式，主要目的在于：① 通过分段线性表示方法降低噪声对模式划分的影响，缩减模式序列的长度，提高相似度量的计算效率；② 把序列形态趋势表示为七元形态模式，使数据的模式表示更贴近数据的实际变化趋势；③ 用最长公共子序列方法计算形态模式距离可避免具体数据点的值对结果产生影响。

下面给出基于分段形态模式的时间序列相似度量算法逻辑：

输入：原始时间序列

Step1选取原始序列的关键点，对序列进行分段线性表示；

Step2对重要点表示的分段序列进行等长处理；

Step3把分段序列表示为斜率序列；

Step4根据每个分段的斜率值确定该子段对应的形态模式；

Step5确定不同序列对应的形态模式序列；

Step6使用递归方法计算不同形态模式序列的最长公共子序列；

Step7根据最长公共子序列计算序列的相似度。

输出：不同序列的相似度值。

3 实验结果与分析

为了检验提出的改进方法的有效性和优势，将本文方法应用于时间序列的聚类工作中。实验环境为Windows操作系统，硬件环境为2.5 GHz CPU，4 GB内存，开发工具为Matlab。

实验数据使用UCI数据库中的Isolet5数据集。从Isolet5数据集中抽取第13类和第14类时间序列，共119条序列，其中第13类包含59个序列，作为类别一，第14类包含60个序列，作为类别二，每条序列包含617个属性。将序列标准化后，通过三种方法进行对比实验。

方法1即欧氏距离方法，不对时间序列进行任何压缩或变换处理，直接进行K-means聚类；方法2即涨落模式方法，不对时间序列进行压缩，直接把时间序列表示成涨落模式序列，然后进行K-means聚类；方法3是本文给出的方法，先对序列进行分段压缩表示，再进行形态模式转换，最后进行K-means聚类。

通过平均查全率和平均查准率对聚类结果进行评估，表2给出了查准率和查全率相关变量说明。

表2 查准率和查全率对应的聚类结果

对比表2中的参数根据查准率和查全率计算公式可以得到聚类结果的平均查全率和平均查准率。

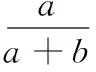
其中n表示样本中的类别数，Pi和Ri表示第i类的查准率和查全率。

使用查准率和查全率公式计算表3中的聚类结果，得到如表4所示的不同方法聚类结果的平均查准率和查全率。从表4可以看出，与方法1和方法2相比，方法3的平均查准率和平均查全率都有所提高。方法1直接对序列计算欧式距离，没有进行维度约简，计算量大而且容易受噪声影响，因此聚类结果不理想；方法2通过划分涨落模式从趋势的角度判断相似度，不受具体数据点值的约束，相对欧氏距离，度量精度有所提高，但是因为直接对原始序列进行模式划分，所以时间复杂度较高，而且噪声的干扰也有一定的影响；方法3首先对序列进行分段表示，实现了维度约简，同时减少了噪声的干扰，然后使用七元形态模式进行表示，不仅能反映形态变化趋势而且能体现变化幅度，与方法1、方法2相比，聚类结果最好，因此本文工作具有有效性和先进性。

表3 三种方法聚类结果

表4 平均查准率和平均查全率

4 结 语

本文针对已时间序列距离度量方法的一些不足，提出了基于形态模式的时间序列相似度量方法。基于分段线性表示的形态模式定义，不仅能降低数据维度，而且能描述序列的变化幅度。在此基础上通过最长公共子序列方法求形态模式序列的相似性，把时间序列的相似性问题转化为字符串匹配问题，提高了计算结果的准确性，而且计算过程相对简单。将本文方法用于时间序列的聚类实验，发现经过适当的参数选取，能取得较好的聚类效果。下一步工作将考虑如何度量非等长时间序列的相似性。

[1] 吴红花,刘国华,王伟.不确定时间序列的相似性匹配问题[J].计算机研究与发展,2014,51(8):1802-1810.

[2] Izakian H,Pedrycz W.Anomaly Detection and Characterrization in Spatial Time Series Data:A Cluster-Centric Approach[J].Fuzzy Systems IEEE Transactions on,2014,22(6):1612-1624.

[3] Suntinger M,Obweger H,Schiefer J,et al.Trend-Based Similarity Search in Time-Series Data[C]//Advances in Databases Knowledge and Data Applications (DBKDA),2010 Second International Conference on IEEE,2010:97-106.

[4] 丁永伟,杨小虎,陈根才,等.基于弧度距离的时间序列相似度量[J].电子与信息学报,2011,33(1):122-128.

[5] Chiu B,Keogh E,Lonardi S.Probabilistic discovery of time series motifs[C]//Siam International Conference on Data Mining,SDM 2009,April 30-May 2,2009,Sparks,Nevada,Usa.DBLP,2003:493-498.

[6] Berndt D J,Clifford J.Using Dynamic Time Warping to Find Patterns in Time Series[C]//Working Notes of the Knowledge Discovery in Databases Workshop,1994:359-370.

[7] Lin J,Keogh E,Lonardi S,et al.A symbolic representation of time series,with implications for streaming algorithms[C]//ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery.ACM,2003:2-11.

[8] 李桂玲,王元珍,杨林权,等.基于SAX的时间序列相似性度量方法[J].计算机应用研究,2012,29(3):893-896.

[9] 刘慧婷,倪志伟.基于EMD与K-means算法的时间序列聚类[J].模式识别与人工智能,2009,22(5):803-808.

[10] 肖瑞,刘国华.基于趋势的时间序列相似性度量和聚类研究[J].计算机应用研究,2014,31(9):2600-2605.

[11] 张海涛,李志华,孙雅,等.时间序列的层次分段及相似性度量[J].计算机工程与应用,2015,51(10):147-151.

[12] 张建业,潘泉,张鹏,等.基于斜率表示的时间序列相似性度量方法[J].模式识别与人工智能,2007,20(2):271-274.

[13] 王钊,汤子健.基于涨落模式的时间序列相似性度量研究[J].计算机应用研究,2017,34(3):697-701.

SIMILARITYMEASUREALGORITHMOFTIMESERIESBASEDONMORPHOLOGICALPATTERN

Wang Rui Jia Ruiyu

(CollegeofComputerScienceandTechnology,AnhuiUniversity,Hefei230601,Anhui,China)

Feature representation and similarity measure of time series is an important foundation of time series data mining. Aiming at the problem that the existing sequence representation method is difficult to reflect the morphological change of the sequence, which leads to the inaccuracy of the similarity measurement results, a new similarity measurement algorithm based on morphological patterns is proposed. On the basis of piecewise linear representation, according to the sequence of slope changes in different periods, the algorithm divides the sequence into different morphological pattern and expresses them with special characters. The time sequence is converted into a sequence of strings. The longest common subsequence method is adopted to calculate the distance of string sequences as the distance between time series. Finally, the effectiveness of the proposed method was verified by experiments. Theoretical analysis and experiments show that the method is insensitive to the value of the data points, which can reduce the interference of noise and has high accuracy.

Time series Similarity Morphological Pattern Slope Sub sequence

TP3

A

10.3969/j.issn.1000-386x.2017.09.049

2016-11-24。国家自然科学基金项目(61202227)；国家科技支撑计划项目(2015BAK24B01)。王瑞，硕士生，主研领域：数据挖掘，数据智能处理。贾瑞玉，副教授。