基于集合的有条件随机智能组卷的研究与实践
梁伟英
(广州市海珠区龙潭小学,广州510315)
基于集合的有条件随机智能组卷的研究与实践
梁伟英
(广州市海珠区龙潭小学,广州510315)
在课堂教学中,根据教学需要利用基于知识点的快速检测试卷对学生的学习情况进行摸查,对提高课堂教学的有效性作用非常明显。基于实际教学需求,在分析快速检测题库的基础上,重点探索基于集合的有条件随机智能组卷的科学性和可行性实施方案,并以案例辅以佐证。
集合;快速检测;组卷;小学数学;案例
0 引言
(1)问题的提出
随着信息技术与教育教学深度融合的不断推进,基础教育教学信息化已进入了一个较高的水平。在课堂教学中,根据教学需要利用基于知识点的快速检测试卷对学生的学习情况进行摸查,对提高课堂教学的有效性作用非常明显,已成为一种被一线教师认可的有效教学策略。目前,小学数学有各种各样的测验试卷、练习册及各类在线考试资源库等,根据这些教学资源构建一个富有学校特色的快速检测题库难度不大,但如何高效、科学、合理的从快速检测题库中智能抽取与教学需求相适应的题目组成一份快速检测试卷,实现教学前测的目的,是一个值得探讨的问题。
(2)研究意义
在小学数学各类题库建设和智能组卷系统中,基于知识点并且允许使用者添加校本特色题目的快速检测智能组卷系统,目前暂时还没有较为成熟的系统。本文讨论的快速检测智能组卷系统的主要研究意义是:基于知识点和教学需求智能产生能适应学校特色的快速检测试卷,目的在于为课堂教学提供教学前测信息,以便提高课堂教学的有效性。
(3)快速检测试卷
在小学数学教学中,为了快速分析学生的学习情况,快速检测试卷的题型主要有:填空题、判断题、选择题。实际组卷时,我们需要根据学习的知识点、根据学情、并按一定的比例组卷。例:人教版小学四年级下册第三单元知识点1,其快速测验试卷的主要结构是:

表1
1 快速检测题库
1.1 库结构

表2
以人教版小学四年级下册第三单元知识点1中的判断题为例,其存储信息是:
编号:XX020402030102001
题目:85+15=15+85
附图:无
参考答案:对
备注:交换加数位置,和不变。
1.2 编号的格式

表3
2 基于集合的有条件智能随机组卷
2.1 组卷要求
按教学实际需要、按学情、按题型、按一定比例科学合理的组卷,最后智能生成试卷和参考答案。
2.2 基于集合的组卷
(1)基本信息
集合M:表示快速检测题库;
集合S:表示快速检测试卷;
集合M1:表示有条件的填空题库;
集合M11:表示按一定要求生成的不重复填空题集;
集合M2:表示有条件的判断题库;
集合M22:表示按一定要求生成的不重复判断题集;
集合M3:表示有条件的选择题库;
集合M33:表示按一定要求生成的不重复选择题集。
(2)集合间的关系
根据集合的定义和每个集合之间的定义,不难证明上述集合存下述关系:
M1⊆M,M2⊆M,M3⊆M
M11⊆M1,M22⊆M2,M33⊆M3
根据编号的唯一性,不难证明下述各集合的交集均为空集。即:
3个子集(M1,M2,M3)两两之间的交集为空集。
3个子集(M11,M22,M33)两两之间的交集为空集。
(3)组卷
S=M11∪M22∪M33
根据编号的唯一性和各个子集之间的关系,集合S的元素具有不重复性(唯一性)。
2.3 实现
(1)生成子集1(M1,M2,M3)
由于各个子集之间都有明显的特征编号,例如填空题其编号第13、14位的特征码为01,因此从集合M抽取并生成3个子集(M1,M2,M3)相对比较简单,其实现方法(以人教版小学四年级下册第三单元知识点1填空题为例)是:
select*from M where编号like'XX020402030101%'
注:实际编程时,为提高运行效率,可以只抽取“编号”字段,即除了集合M、S之外,其他所有子集的元素只有一个字段(编号)。
(2)生成子集2(M11,M22,M33)
在已有子集(M1,M2,M3)的基础上生成有题量要求的新子集(M11,M22,M33),其实现方法有多种多样,但考虑到组卷的效率和教学需求,根据笔者的研究与实践,下述实现原理是非常高效的(以从100题填空题中抽取3题为例)。
①随机产生一个不超过100的正整数K(1到100);
②取出集合M1中顺序号为K的编号放入集合M11;
③将顺序号为K的编号与顺序号为100的编号互换
④随机产生一个不超过99的正整数K(1到99);
⑤取出集合M1中顺序号为K的编号放入集合M11;
⑥将顺序号为K的编号与顺序号为99的编号互换;
⑦随机产生一个不超过98的正整数K(1到98);
⑧取出集合M1中顺序号为K的编号放入集合M11;
⑨将顺序号为K的编号与顺序号为98的编号互换。
根据上述抽取原理,经过互换之后抽取过的编号将是集合M1的最后一个元素,而下一次抽取的元素最大数是上一次元素总数减1,即不会抽取最后一个元素。因此,经过上述9条指令之后,集合M11中将存放有3个不重复的编号。其计算机编程原理是:
for(int i=0;i<3;i++)
{
①随机产生一个不超过(100-i)的正整数K(1到100-i);
②取出集合M1中顺序号为K的编号放入集合M11;
③将顺序号为K的编号与顺序号为(100-i)的编号互换。
}
(3)组卷
根据子集(M11,M22,M33)中的编号,依次从集合M中抽取相应的题目,即可智能生成试卷和参考答案。其中从集合M中抽取相应的题目的实现方法(以M11中的题目为例)是:
select*from M whereM.编号=M11.编号
//上述代码以SQL语句为例,具体实现代码也可以选择其他的实现代码。
2.4 拓展
(1)拓展1:有难度系数的题目
如果题目有难度系数之分,那么编号中的第15位将用于表示难度系数。例:最后3位为301,表示难度系数为“难”的第1题;最后3位为201,表示难度系数为“中”的第1题;最后3位为101,表示难度系数为“易”的第1题。其组卷方法也与上述方法相类似。
(2)拓展2:指定题目
如果任课教师希望通过自选题组卷,其组卷原理也与上述方法相类似。唯一差别在于计算机智能组卷改为教师手动组卷(经过计算机提前筛选,教师在指定范围中选题)。
(3)拓展3:基于翻转课堂的课外前测
本系统可应用于翻转课堂的教学前测。此时,由于小学数学前测题目的特殊性(答案一般具有唯一性),学生的学习情况测试将由计算机自动阅卷,并自动形成分析报告。
2.5 科学性与合理性
为了提高快速检测试卷的科学性与合理性,在题库建设过程中,某一知识点的填空题、判断题、选择题原则上各聚焦一个需要解决的问题。
3 案例
3.1 快速检测试卷
例:人教版小学四年级下册第三单元知识点1快速检测试卷,其具体要求如下:
知识点:加法运算定律(标记:XX04020301)

表4
3.2 组卷
(1)生成子集(SQL语句)
Select编号from M where编号like'XX0204020301%'
//生成集合M1
Select编号from M where编号like'XX0204020302%'
//生成集合M2
Select编号from M where编号like'XX0204020303%'
//生成集合M3
(2)生成具体试卷的抽取代码(样例)
以C#语言为例,从80道选择题中抽取不重复的2道题,其编号抽取代码如下:
intmys=2;
intzs=80;
for(int i=0;i { Random k=new Random(); k=System.Convert.ToInt16(Math.Floor(myseed.NextDouble ()*(zs-i))); m11[i]=m1[k]; m1[k]=m1[zs-i-1]; m1[zs-i-1]=m11[i]; } //数组m1表示集合M1,数组m11表示集合M11 3.3 样卷 一、细心读题,谨慎填写。(共30分)1、78+=44+78 2、49+51+96=96+(51+) 二、巧思妙断,判断对错。(共30分) 1、算式425+14+186与14+186+425的计算结果相同。() 2、27+65+73+35=(27+73)+(65+35)() 三、反复比较,择优录取。(共40分) 1、与83+17+24不相等的算式是()。 A.24+(83+17)B.83+31 C.100+24 2、107+85+93+15()107+93+(85+15) A.=B.>C.< 3.4 前测结果 知识点:加法运算定律(标记:XX04020301) 表5 3.5 教学策略与教学效果 (1)教学策略 根据前测的结果,笔者发现学生对两数相加、交换加数的位置、结果不变的道理掌握得较好。但学生在没有应用加法运算定律前,对于上述题目常使用以前的计算方法,导致容易计算或判断错误。因此,本节课的教学重点是引导学生发现在加法运算中的运算定律,从而学会用运算定律进行加法的简便运算。为此,笔者在课堂教学中调整了相应的教学安排,减少了在加法中“交换加数位置,和不变”的举例说明,有意识的引导学生进行分组讨论,加强加法运算定律在实际计算中的运用,重点引导学生善于使用这些运算定律解决实际问题。 (2)教学效果 在单元测验中,本知识点学生的掌握情况好,测验结果令人满意,得分率在97%左右。 实践证明,基于知识点、以满足教学需求为目标的快速检测试卷,在课堂教学中,能为教师提供有效的教学前测信息,能极大地提高课堂教学的有效性。基于集合的有条件随机智能组卷策略,有利于减轻教师的工作量,有利于提供更加全面的前测信息,有较高的科学性与合理性。文中提及的代码全部在真实环境下测试通过,并应用于实际工作中,应用效果好。 Research and Practice ofConditional IntelligentGenerating Test Paper Based on Set LIANGWei-ying In the classroom teaching,according to the teaching needs,the use of knowledge based rapid testpapers for students to study the situation, to improve the effectiveness of classroom teaching is very obvious.Based on the analysisof the rapid testquestion bank,focuses on the ex⁃ploration of scientific and feasible implementation scheme of the conditional intelligentgenerating testpaper based on set,and provides the practical casesas the supportevidence. 梁伟英(1972-),女,广东广州人,本科,研究方向为小学数学、教学信息化 2017-05-11 2017-07-26 海珠区教育科学“十二五”规划课题(No.2013C062) 1007-1423(2017)22-0032-04 10.3969/j.issn.1007-1423.2017.22.007 Set;Rapid Test;Generating TestPaper;ElementaryMathematics;Case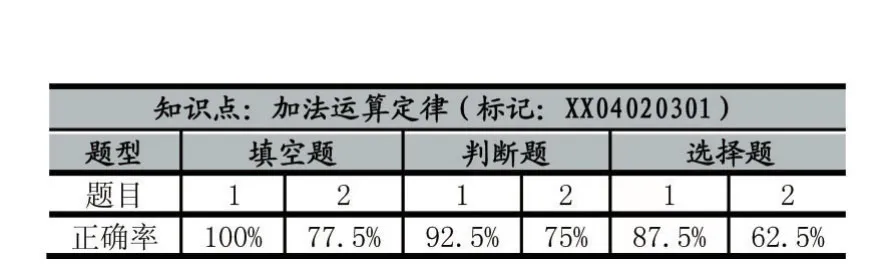
4 结语
(Longtan Primary SchoolofHaizhu DistrictofGuangzhou,Guangzhou 510315)

