基于旋轮线方程拓展的防伪底纹设计

黎世伦，曾萱，丁贺，姚正安

（1.广东实验中学，广州510375；2.中山大学附属中学,广州510275；3.中山大学数学学院,广州510275）

基于旋轮线方程拓展的防伪底纹设计

黎世伦1，曾萱2，丁贺2，姚正安3

（1.广东实验中学，广州510375；2.中山大学附属中学,广州510275；3.中山大学数学学院,广州510275）

旋轮线是数学中众多的迷人曲线之一，直线上的旋轮线、圆外与圆内旋轮线是经典的旋轮线。旋轮线方程依赖3个参数，不同的参数设置，曲线图案很不一样，其多变的图案可用于底纹防伪。经典的旋轮线的曲线图案比较单薄。对经典的旋轮线，利用曲线平移叠加、缩放叠加技术，使之更漂亮和丰满。同时，把旋轮线方程推广拓展为4参数或9参数情形，使得曲线变化更复杂和精妙，并利用程序生成图形丰富的花边、团花等防伪底纹。

旋轮线；防伪底纹；花边；团花

1 防伪底纹设计

从自己的口袋中拿出一张任意面值的人民币或身份证仔细观察，就能发现上面的美丽的底纹。底纹的作用是由于身份证件和钞票等关系重大的印刷物品，无一例外的需要具备诸多的防伪特性。

底纹的防伪作用主要体现在图案的复杂性及防复制功能。印刷中常用的防伪底纹元素有：团花、花边、浮雕、潜影、缩微文字等。花边就是用于印刷在产品的边缘，用各种不同的复合式花边，通过变化它的元素和色彩达到装饰和防伪的作用。团花是在防伪标签上面印刷各种鲜花的版纹，在防伪的同时也具有较高的技术欣赏。还可以通过与产品和公司形象的结合设计个性化的团花防伪标签。

随着计算机技术的发展，使用计算机创作的底纹效果，制作特别复杂、细微、精致、高分辨力的印品底纹。如任意的几何图形，单线、复合或扭曲封闭式的花边、或十分复杂的团花等图形。这种底纹用人工、照排或扫描均难以复制。

目前国外防伪底纹软件有Cerber，Jura，Barco等，国内有方正超线、蒙泰版纹、爱明天等。例如Jura在版纹防伪技术上较为先进，号称在全世界范围内为76个国家设计钞票；北大方正超线防伪底纹设计系统使用的线条是正弦线[1]。

旋轮线是与正弦曲线类似但更为复杂，它被广泛应用于齿轮的设计[2-3]。本文讨论旋轮线，并对它进行拓展，利用它们生成更复杂精美的团花和花边等防伪底纹。

2 经典的旋轮线

直线上的旋轮线是这样定义的：一个圆沿一直线滚动，则圆上一定点所经过的轨迹称为旋轮线（cy⁃cloid），又称摆线。旋轮线也是最速降线问题和等时降落问题的解[4]。

考虑半径为a的圆，定点的初始位置为坐标原点O，定直线为x轴。当圆滚动θ角以后，圆上定点从O点位置到达另一位置，切点在圆上经过的距离与在直线上经过的距离相等，均为aθ。从而此时的横坐标为aθ-a sinθ，纵坐标为a-a cosθ。因此，此旋轮线的参数方程为：

其中a为圆的半径，q是圆的半径旋转的角度（滚动角）。

除直线上的旋轮线外，经典的旋轮线还包括圆内或圆外旋轮线。如果让动圆沿着一个定圆滚动，而不是沿着直线滚动的话，我们将得到圆内旋轮线（hypocy⁃cloid）或圆外旋轮线（epicycloid）[4]。设定圆半径为R，动圆半径为r，动圆上的某定点（可在圆周上、圆内、圆外）到动圆的中心的距离是d。当动圆沿着定圆外侧滚动时，动圆上的定点所形成的轨迹，称为圆外旋轮线，其参数方程为：

可类似求得动圆沿着定圆（R>r）的内侧滚动得到的圆内旋轮线的参数方程为：

当d=r，定点在圆周上，dr，点在圆外，对应的旋轮线为长幅旋轮线。

3 旋轮线曲线平移叠加与缩放叠加技术

旋轮线与北大方正超线类似，使用正弦、余弦函数，从旋轮线方程可以发现，定圆半径R、动圆半径r、定点（可在圆周上、圆内、圆外）到动圆的中心的距离d的改变，会产生形态各异的曲线。就是这种特殊性，旋轮线可用于防伪底纹的生成。然而，直接用这些曲线作为防伪底纹，略显单薄。亓文法等人[5]放松了固定摆点的条件，利用动摆点旋轮线生成防伪底纹。此研究对动摆点的轨迹有所限制，滚圆自转一周，要求动摆点也沿着自己的轨迹也自转一周；另外，动摆点的轨迹需要通过采样形成摆点集，用摆点集形成的多边形对动摆点的轨迹进行近似，程序实施较麻烦。下面我们另辟新径，在经典旋轮线的基础上，通过三种技术来生成防伪底纹：曲线平移叠加、缩放叠加与方程拓展，实现防伪花边与团花的设计。

3.1 平移叠加技术

我们把基本的圆内或圆外旋轮线通过多次平移，每次对上一个图形往右平移c个单位，则只需要把原来的参数方程中的x的值增加c，即：

通过多次平移，然后叠加到原来的图形上，重复多次，可生成条状花边。

3.2 缩放叠加技术

我们把基本旋轮线按照一定比例缩小尺寸，叠加到原来的图形上。如此重复叠加多次，使原始图形逐渐变得丰满美观，生成防伪团花。

我们对基本的短幅内旋轮线:R=11，r=7，d=4通过20次缩放叠加与平移叠加分别生成图1中的团花与花边。其中团花是通过20次按比例缩小叠加形成，第1次、第2次、…、第20次叠加时尺寸时为原始基本图形尺寸的1/1.25、1/1.5、…、1/5。

图1 圆内旋轮线（R=11，r=7，d=4）的缩放叠加与平移叠加生成的团花与花边

4 旋轮线方程拓展技术

我们将旋轮线方程进一步推广，在参数方程中，在x轴增加旋转角度θ的线性项，就可以产生更复杂、更美丽的防伪花边和团花等图案了。

4.1 圆内或圆外旋轮线方程拓展式

在前面的讨论中，我们知道，在直线上（不妨设为x轴）滚动的旋轮线，在x轴有aθ项，使得曲线形状呈现为条状。因此，我们把圆内或圆外旋轮线在x轴增加θ的线性项cθ，拓展为:

圆内旋轮线拓展式:

此拓展旋轮线曲线形状依赖4个参数R，r，d，c.当c=0时，上面拓展式即退化为标准的圆内或圆外旋轮线。当c≠0时，由于线性项cθ的影响，曲线为条状，适宜作为花边。图2为c≠0时的拓展的旋轮线生成的各种花边图案。

图2 四参数拓展圆内或圆外旋轮线旋轮线生成的花边

4.2 更一般情形的旋轮线方程拓展式

下面考虑更为复杂的旋轮线方程推广，利用拓展方程，可以生成非常复杂的防伪花边、团花和底纹。在直线上滚动的旋轮线与圆内或圆外旋轮线的参数方程，可以统一到如下的拓展形式：

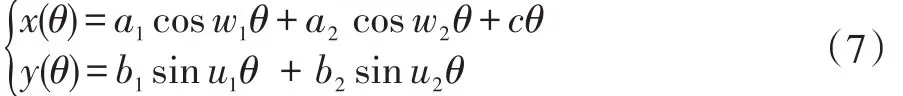
其中w1>0,w2≥0,u1>0,u2≥0,a1,b1,a2,b2不为0。

对于此拓展形式的曲线，下面我们探讨其周期性，并把周期性用于底纹设计。

引理［1］：假设f1(t),f2(t)都是定义在实数集上的周期函数，若f1(t),f2(t)连续，则下面三个条件等价：

（i）f1(t)+f2(t)为周期函数;

（ii）f1(t)与f2(t)存在公共周期;

（iii）存在这两个函数的正周期使得这两个正周期之比为有理数。

实际上，此引理对两个函数之一连续（即f1(t)或f2(t)连续）的情形也成立[7]。

定理（周期性判别定理）：当且仅当c=0，且w2/w1,u2/u1与都为有理数时，则曲线（7）关于参数q有周期，即存在T>0，使得：

证明：（1）考虑c=0的情形。

当常数w不为0时，三角函数cos wθ（或sin wθ）为周期函数，具有周期2kπ/w，这里k为整数。由引理知，当且仅当为有理数时，x(θ)具有周期；当且仅当u2/u1为有理数时，y(θ)具有周期。当且仅当w2/w1,u2/u1与都为有理数时，x(θ)与y(θ)具有公共周期。

（2）考虑c≠0的情形。

反设此时x(θ)具有周期T，则对任意整数k，有x(θ+kT)=x(θ)。

任取一实数θ0，连续函数x(θ)在闭区间[θ0,θ0+T]上有界，即存在常数M，使得|x(θ)|≤M对任意θ∈[θ0,θ0+T]成立。

当c≠0时，有lθi→m∞|x(θ)|=∞，则存在一点θ*，成立|x(θ*)|>M。对于此θ*，比存在整数k*，使得θ*+k*T∈[θ0,θ0+T]，则有：

|x(θ*)|=|x(θ*+k*T)|≤M。

与|x(θ*)|>M矛盾。故c≠0，x(θ)为非周期函数。

若曲线（7）关于参数q有周期，我们只需要画出q在[0，T]上取值的轨迹。然而，当曲线（7）关于q没有周期时，q在不同长度区间上的轨迹不同。例如，我们取a1,a2,b1,b2,c,w1,w2,u1,u2分别为2，p，2.5，p，0，2，e，1.5e，1，10，根据周期性判别定理，此曲线没有周期性。我们画出θ∈[0,20π]与θ∈[0,100π]上的此曲线轨迹，见图3。

图3 (2,π,2.5,π,0,2,e,1.5e,1,10)对应的拓展旋轮线

旋轮线拓展曲线的图形取决于9个参数：a1,a2,b1,b2,c,w1,w2,u1,u2，若它为非周期函数，图形还依赖q的取值范围。参数个数的增加，使得曲线更加丰富多样。通过作图程序，实现不同的参数下形成的轨迹，可生成更复杂的防伪花边与团花。

我们采用数学软件Mathematica，设置不同的参数，根据拓展方程生成拓展的旋轮线曲线图。当c=0时，曲线图案为团花。当c≠0时，曲线图案为条形的花边，如图4。相应的Mathematica程序：

SecPlot[a1_，a2_，b1_，b2_，c_，w1_，w2_，u1_，u2_，N_]:=ParametricPlot[{c t+a1 Cos[w1 t]+a2 Cos[w2 t]，b1 Sin[u1 t]+b2 Sin[u2 t]}，{t，0，N*2 Pi}，Mesh->1，Axes->False]

SecPlot[2，Pi，1，Pi，0，2，E，2E，2，20]

5 结语

底纹防伪是成本低且防伪效果很好的一种防伪印刷技术。我们推广拓展后的旋轮线形状参数较多，图形精美复杂，使得仿制者对所复制印刷品很难获知曲线的参数组合设置情况，从而难以制作出类似的效果。

图4 九参数拓展旋轮线生成的团花与花边

[1]李霞.安全底纹设计在印刷产品中的应用.印刷杂志，2008，1:51-53.

[2]Chen B.K.，Fang T.T.，LiC.Y.，etal.GearGeometry ofCycloid Drives[J].Science China Technological Sciences，2008，51（5）:598-610.

[3]Ge X.G.，Li J.，Wang L.P.，etal.Application of cycloid inmachining polygon parts[J].Machine Tool&Hydraulics，2005.

[4]Whitman，E.A.Somehistoricalnoteson the cycloid.The American MathematicalMonthly，1943，50（5）:309–315.

[5]亓文法，李晓龙，杨斌，国伟，卢书一.动摆线及其在安全底纹设计中的应用[J].计算机辅助设计与图形学学报，2008，20（2）: 267-272.

[6]Fink A.M.AlmostPeriodic Differential Equations.Lecture Notes in Mathematics，1974，377:80-112.

[7]刘长剑，汤正谊，LIUChang-jian等.两个周期函数的和的周期性[J].大学数学，2016，32（4）:82-84.

Security Pattern Designs Based on Extended Cycloids

LIShi-lun1，ZENGXuan2，DINGHe2，YAOZheng-an3
（1.Guangdong ExperimentalHigh School,Guangzhou 510375；2.Middle School Affiliated to Sun Yat-sen University,Guangzhou 510375；3.SchoolofMathematics,Sun Yat-sen University,Guangzhou 510275）

Cycloid is one of themost fascinating curves inmathematics.Cycloids,epicycloids and hypocycloids belong to the family of classic cy⁃cloids.The graph ofcycloid dependson three parameters.Differentparametersettingsmay lead to very differentpatterns.This kind ofprop⁃erty ensures the diversity if they are used in security pattern designs.The patternsof classic cycloids are too simple.Sowe used translation, scalingand overlay techniques tomake classic cycloidsmorebeautifuland plentiful.Simultaneously,weextended classic cycloids to agen⁃eral casewith 4 or9 parameters,in order tomake the curvemore sensible to the parameters.We also illustrate some security pattern exam⁃ples,such asbordersand rosettes,by using ourmethods.

黎世伦（2000-），男，高中，中国科协英才计划

姚正安（1960-），男，博士，教授，博导，院长，研究方向为信息安全技术、偏微分方程

2017-07-20

2017-08-01

国家自然科学基金重点基金项目（No.11431015）

1007-1423（2017）22-0006-05

10.3969/j.issn.1007-1423.2017.22.002

Cycloid;Security Pattern;Border;Rosette