元素分布构建的三维模型表面纹理合成方法*
桂 彦,刘 杨+,李 峰
1.长沙理工大学 计算机与通信工程学院,长沙 410114 2.长沙理工大学 综合交通运输大数据智能处理湖南省重点实验室,长沙 410114
元素分布构建的三维模型表面纹理合成方法*
桂 彦1,2,刘 杨1,2+,李 峰1,2
1.长沙理工大学 计算机与通信工程学院,长沙 410114 2.长沙理工大学 综合交通运输大数据智能处理湖南省重点实验室,长沙 410114
针对由纹理元素组成的样本纹理在模型表面纹理合成中难以保持样本纹理结构规律性的问题,提出了一种基于纹理元素分布构建的模型表面纹理合成方法。首先通过用户交互在三维模型表面上确定待合成纹理的初始位置,然后利用邻域比较以局部扩张-冲突检测的形式,从三维模型表面初始位置上开始逐步构建纹理元素的分布,使之与二维样本纹理的纹理元素分布具有一定的外观相似性。最后,采用自适应的局部参数化方法将纹理元素分别映射到模型表面对应位置,以获得最终的三维模型表面纹理合成结果。实验结果表明,该方法能够在模型表面合成高质量的纹理,并在保持纹理元素完整性和保持样本纹理潜在规律性的同时,能够使得已合成纹理中扭曲程度较低且是连续、无接缝的。
模型表面纹理合成;纹理元素分布;邻域比较;局部扩张
1 引言
纹理合成是计算机图形学和计算机视觉领域的研究热点之一。模型表面纹理合成是在三维模型表面上合成纹理,以丰富模型表面细节,从而增强场景中三维模型的真实感。在进行模型表面纹理合成时,最常用的是基于样本的纹理合成方法[1-9],即以给定的小块二维样本纹理为参照,在模型表面上合成具有相似外观的大块纹理图像。由于样本纹理是二维图片,而待合成的纹理位于模型表面上,因此现有的模型表面纹理合成方法一般通过对模型全局参数化,以建立合成纹理所在二维平面和三维模型表面之间的全局映射[2];或者将样本纹理中的像素点直接映射到模型顶点上[3-6],以及直接在三维表面上拼接和缝合样本纹理子块[7-9],从而获得最终的模型表面纹理合成结果。
这些方法对于处理随机纹理(如水波、草地、沙粒等纹理)时能够产生理想的合成结果,然而对于由离散纹理元素组成的规则或近似规则的纹理(如豹纹、墙面、布料等纹理)时,合成的纹理中容易产生破裂的纹理元素,使得无法获得连续的纹理结构。其主要原因在于:全局参数化的模型表面纹理合成方法[2]由于受到模型表面曲率的影响,合成结果中会出现扭曲变形或者不连续的问题。而直接在模型表面进行纹理合成的方法[3-9]虽然能够在三维模型上合成较为连续的纹理,但合成过程中需要进行大量邻域匹配搜索,且很少考虑利用样本纹理中纹理元素之间的空间位置关系,使得该类方法不仅合成效率较低,而且仍然难以保持样本纹理潜在的结构规律性。
针对现有方法中存在的这些问题,本文提出了一种基于纹理元素分布构建的三维模型表面纹理合成方法。该方法通过参照二维样本纹理中纹理元素的分布,能够在三维模型表面上合成新的纹理元素的分布,并且使其与二维参照分布具有一定的外观相似性。另一方面,在获得已合成的纹理元素分布之后(即提供了纹理元素在模型表面的位置信息),通过采用局部纹理映射方法,将从二维样本纹理中提取的纹理元素映射到模型表面相应位置上,以达成在三维模型表面上有效合成纹理的目的。实验结果表明,本文方法能够获得与二维样本纹理具有较相似外观的三维模型表面纹理合成结果,且在合成结果中不仅能够保持纹理元素的完整性,而且还能有效地减小纹理元素的拉伸及扭曲变形。
2 相关工作
近年来,对于如何高效地合成由离散纹理元素组成的纹理,国内外许多研究学者在该领域中做了大量的创新性工作。2002年,Dichler等人[5]提出了一种基于“纹理粒子”的方法,该方法首先将样本纹理分割成纹理粒子,然后根据粒子的共现关系在三维模型表面上合成纹理。2006年,Barla等人[10]提出了一种基于元素邻域相似性的合成方法,该方法采用Delaunay三角剖分建立元素的空间相邻关系,合成时先在二维平面上随机生成种子,并依据邻域比较逐一用元素替换种子点,从而得到二维平面上的合成结果。2008年,Takashi等人[11]在此基础上引入种子的局部扩张,能够有效合成与参照具有相似外观的新元素的分布。2009年,Hurtut等人[12]提出了一种统计模型分析元素分布规律,通过学习样本中同一类型元素的空间关系以及不同类型元素之间的空间关系,从而在平面上生成外观相似度较高的2D非真实感图像。2010年,Passos等人[13]提出了一种元素碰撞的概念,能够对合成结果中元素的局部密度进行控制。同年,Gui等人[14]提出了一个基于基元的周期纹理分析与合成方法,该方法能够有效保持合成纹理中基元的结构规律和基元完整性。上述方法[10-14]均以纹理元素为基本单位,通过构建并利用纹理元素之间的相邻关系,从而根据提供的样本纹理在二维平面上能够生成具有较相似外观的纹理或图像。然而,由于元素之间空间位置关系在三维模型表面上和二维平面上差异较大,直接将这些方法应用到三维模型表面上时,纹理元素的分布难以保持其潜在的规律性,因而合成的纹理容易产生扭曲和不连续的现象。
同时,研究者们也提出了很多三维模型表面纹理合成方法,通过直接在三维表面上生成新的纹理,以避免扭曲和不连续的问题,本文方法也属于这一类。2003年,Zhang等人[6]根据用户提供的方向场和渐变函数对目标纹理中的邻域进行变形,以在三维模型表面上生成逐渐变化的纹理。2005年,Lefebvre等人[8]提出了一种交互纹理合成方法,通过利用存储的纹理元素及其位置信息,并以局部映射的方法在三维模型表面合成纹理,这不仅有效减少了内存开销,还避免了对模型进行全局参数化。2006年,Lefebvre等人[9]进一步提出了一种创建新外观空间的预处理方法来进行模型表面纹理合成。该方法在进行合成前先将样本纹理变换到外观空间,并使用间接映射表处理边界处的邻域采样问题,避免了合成结果中的不连续问题。2008年,Chen等人[15]提出了一种基于多尺度邻域纹理合成方法,该方法能够在模型表面生成高质量的纹理合成结果。2010年,Chen等人[16]提出了一种基于规则块局部重采样的纹理合成方法,该方法首先在模型表面生成向量场,并根据重采样信息生成纹理。同年,Dischler等人[17]提出了一种基于过程纹理粒子的纹理合成方法,以可置换的视觉元素分布的方式定义纹理,从而为表面添加高分辨率的纹理。2011年,Ma等人[18]提出了一种离散纹理合成方法用于合成由几何元素所组成的几何纹理。在该方法中,用户为样本纹理中的每一个离散几何元素指定一个或多个采样点,根据这些采样点之间的空间位置关系,并反复调整合成域中种子的位置,以提高所合成纹理与样本几何纹理之间的视觉相似程度。2015年,Huang等人[19]提出了一种利用基元分布的模型表面合成方法,该方法首先在三维模型表面上随机添加种子,再根据样本纹理中基元的邻域信息对种子进行调整,从而在模型表面合成近似规则纹理。虽然上述方法能够直接在三维模型表面上进行纹理合成,一定程度上减少了纹理映射带来的纹理失真。但受三维模型表面曲率变化的影响,合成结果中的纹理元素容易受到破坏,其位置也容易产生偏移,从而导致合成纹理中纹理结构的连续性难以保持。因此,在三维模型表面合成纹理时,如何同时保持纹理元素的完全性和纹理的结构规律,是三维模型表面纹理合成的一个重要研究方向。
3 三维模型表面纹理合成
3.1 模型表面分布构建算法概述
为了在三维表面上进行纹理合成,本文首先需要在三维模型表面上进行纹理元素分布的构建,即根据从样本纹理中提取出的二维纹理元素分布,在模型表面上确定待合成纹理中所有纹理元素的具体位置(“种子”,后续文中均以种子代替纹理元素的位置)。给定一幅样本纹理,用户交互定位样本纹理中所有完整的纹理元素,即排除位于样本纹理边界而产生区域部分缺失的纹理元素,将纹理元素的最小包围盒的中心作为纹理元素的位置。将这些纹理元素的位置看作离散的点集,通过对其进行Delaunay三角剖分,并在每两个相邻的纹理元素之间构建一条连通边,从而能够建立纹理元素之间的连通关系(如图1所示)。对于其中任一纹理元素eref,所有与其直接相连接的纹理元素构成其邻域ω(etar),且邻域ω(etar)包含了以纹理元素eref为中心的局部区域中纹理元素的相对位置和种类信息。
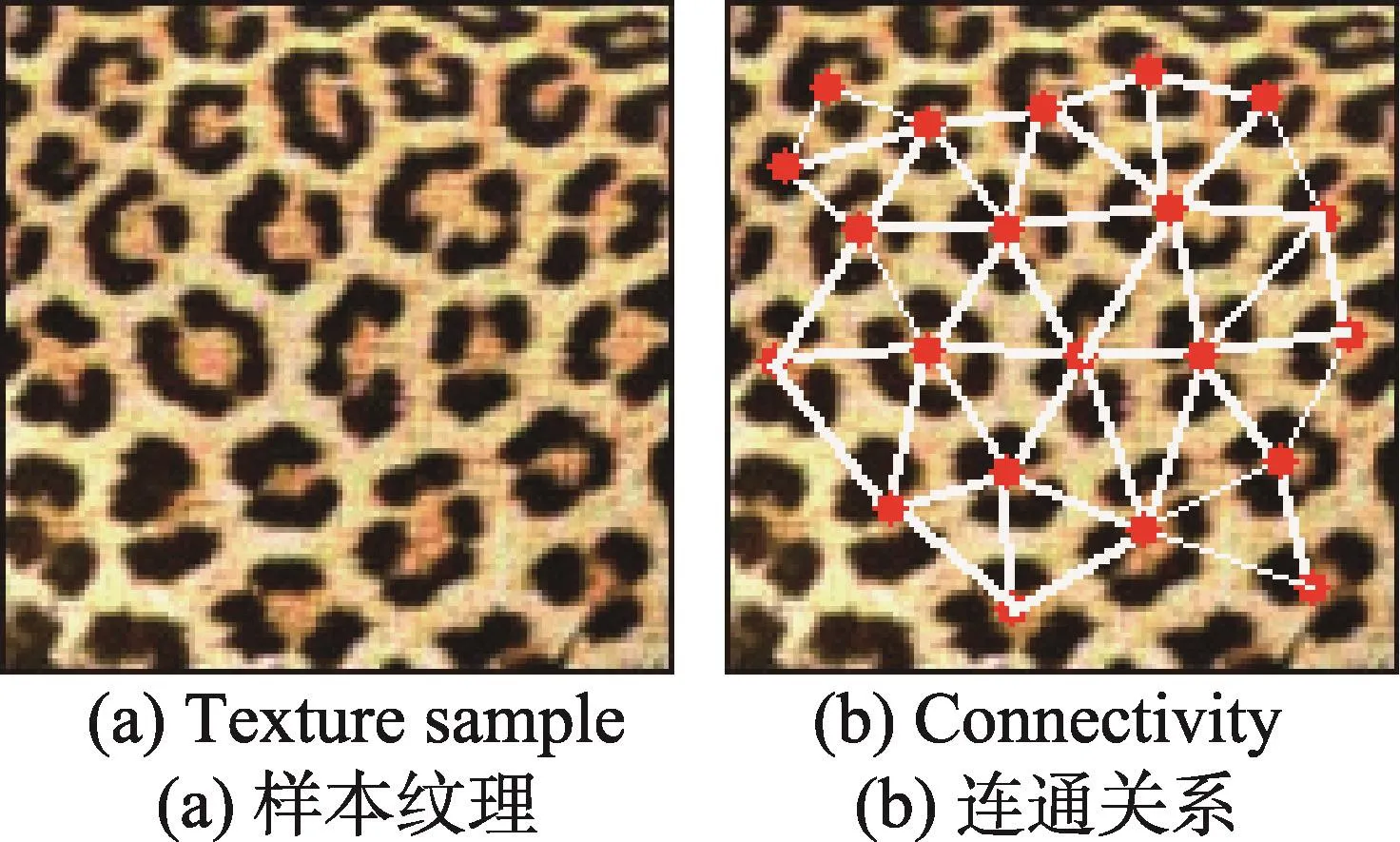
Fig.1 Connectivity construction图1 连通关系示意图
当获得了二维纹理元素的分布之后,在三维表面上,从用户指定的初始位置开始逐步构建纹理元素的分布。
步骤1首先在三维模型表面上确定初始位置(初始的种子),然后从参照连通关系中选择信息最丰富的邻域(即具有足够多的相邻纹理元素)放在所选初始位置上。
步骤2在三维表面上选择离初始种子测地距离(geodesic distance)最短的种子作为下一次扩张的中心种子。
步骤3采用改进的邻域比较方法,从参照连通关系中选取最佳匹配邻域,将中心种子的邻域中缺少的纹理元素作为待添加的种子(详见3.1.1节)。
步骤4通过对三维模型进行候选点采样,并根据待添加种子相对中心种子空间位置信息,选择最佳的候选点作为新种子在三维模型表面上的位置(详见3.1.2节)。
步骤5对新添加种子进行冲突检测,移除发生位置冲突的种子(详见3.1.2节)。
步骤6重复步骤2到步骤5,直到种子覆盖了整个三维模型表面,从而最终获得三维表面上的纹理元素的分布。
上述三维模型表面纹理元素分布构建的过程以及步骤4和步骤5的详细处理过程由如算法1描述。
算法1模型表面分布构建算法


由算法1可知,假设样本纹理中纹理元素数量为m,合成的纹理元素数量为n,那么步骤2~5的时间复杂度分别为O(n)、O(m)、O(m)和O(nlbn)。因此,上述纹理元素分布构建算法的总时间复杂度为O(n2lbn)。
3.1.1 最佳匹配邻域选取
最佳匹配邻域的选取是保证合成分布外观相似性最重要的部分,这直接关系到模型表面纹理元素分布构建的效果。设ω(eref)为样本纹理中与纹理元素eref直接相邻的纹理元素组成的邻域,同理ω(etar)为待合成纹理元素分布中纹理元素etar的邻域。需要指出的是,此处的纹理元素均为种子。本文采用邻域比较(neighborhood comparisons)方法[12]度量邻域ω(eref)和邻域ω(etar)之间的相似程度,即比较两个邻域中所有纹理元素在相对位置和类别上的差异。然而,由于参照的纹理元素分布是二维的,而模型表面上待构建的种子与种子之间的分布却是三维的,现有的二维邻域不能直接进行比较。因此,在进行邻域比较之前,本文方法需要采用投影变换方法将模型表面上当前所选中心种子及其邻域映射到基平面S0,即以所选中心种子所在三角面片为基平面,从而产生与模型表面种子分布相对应的二维平面上的种子分布(图2(a));再将映射后的邻域与样本纹理中纹理元素的邻域进行比较,以确定待添加的新种子,进而使得能够有效地在模型表面上进行种子的扩张。在三维模型表面上,由于邻域中各种子与中心种子的距离很短,以及各种子所在三角形面片与基平面的法向差异也很小,因而邻域中各种子分布的方向性将不受投影变换的影响。由此,可以根据投影后的分布获得模型表面上待添加新种子的方向信息,以及确定待添加新种子与中心种子之间的空间距离。
设ω(etar)中有m个种子,ω(eref)中有n个种子,且满足n≥m的条件。将ω(etar)中的每个种子依次与ω(eref)中的各种子进行匹配,即为每一个种子指定一个不重复的种子。由此,可以获得邻域 ω(etar)和 ω(eref)之间的一个匹配,其中匹配 f中的种子是一一对应的。一旦获得邻域ω(etar)和邻域ω(eref)之间的匹配集F,其含了个匹配 f,度量投影后的邻域ω′(etar)和邻域ω(eref)之间差异的误差函数定义如下:

通过逐个比较各匹配 f下邻域ω(etar)和邻域ω(eref)之间的误差 Error(ω′(etar),ω(eref)),当邻误差 Error(ω′(etar),ω(eref))为最小值时,可以在样本纹理中找到与当前所选种子邻域ω(etar)最相似的邻域ω(eref),并获得最佳匹配 fbest,如图2(b)所示。对比最佳匹配 fbest中邻域ω(eref)与邻域ω(etar)之间一一对应的种子信息,能够获得n-m个待添加种子和与之分别对应的样本纹理元素,并获得待添加新种子的相对位置信息和。待添加种子用X标记,如图2(c)所示。

Fig.2 Illustration for neighborhood comparisons图2 邻域比较示意图
3.1.2 模型表面种子的局部扩展
将获得的添加种子的相对位置信息作为在模型表面种子扩张的依据,即以作为待添加新种子与模型表面上中心种子etar之间的空间距离;而方向角则用于确定待添加新种子相对于中心种子etar的偏移程度。由此,以中心种子etar的位置为球心P0,并以当前所选待添加种子与中心种子etar之间的空间距离为半径作一个球O。此时,可由方向角和球心P0得到与基平面S0垂直的平面Sθ。当三维模型上某一面片St、平面Sθ与球O相交于点P时,交点P即为待添加种子在三维模型表面上的位置,如图3所示。

Fig.3 Position of seeds to be added图3 模型表面待添加种子的位置

其中,P0表示中心种子etar在三维模型表面上的位置;Pt是面片St内一点;V(P0,P)表示从P0到P的方向向量;nt为面片St法向量;n0是平面S0的法线;nθ是平面 Sθ的法线。
事实上,虽然通过求解上述方程组能够精确地计算待添加种子在模型表面上的位置,但复杂度高,容易导致时间效率低下,难以达到实时计算的要求。因此,本文首先在模型表面的某一三角形面片所在平面St上选取W个候选点,然后用所有候选点依次替代P。当取得最小值时,为P最近似的位置估计。需要指出的是,候选点要尽量地分布均匀。当候选点数量增多时,随着计算量的增加,所估计的模型表面纹理元素的位置也就越准确。也就是说,通过在三角面片上选取一定数量的采样点,使得能够将复杂的方程组求解问题转化为种子近似估计问题,从而极大地提高了待添加种子位置计算的效率。

Fig.4 Collisions detection图4 冲突检测示意图
此外,由于邻域比较和扩张中产生的误差累计,待添加种子和三维模型表面上已合成的种子会产生冲突,导致种子分布出现过于稀疏或者过于密集的情况。因此,每当在三维模型表面增加新种子时,需要对其进行冲突检测,并修正已构建的种子分布,以降低误差累计带来的影响。检测的冲突类型主要包括两类:区域冲突检测和种子间冲突检测(图4(a)和图4(b))。区域冲突是指在已合成种子的邻域覆盖区域内添加新种子,从而产生过于密集的分布。当新添加种子位于中心种子邻域覆盖区域(图4中深灰色区域),则删除种子及其所有连接边;当新添加种子位于其他种子邻域覆盖区域(图4中浅灰色区域),则保留种子,但在之后的合成过程中不再以该种子作为中心种子进行邻域的比较和扩展。种子间的冲突是指当新添加种子和已合成的某一种子之间的距离过短(l<lshort)时,将新添加种子及其所有连通边合并到该种子内,其中lshort是三维模型表面上已合成种子之间最短连接边中的长度。按照上述方法进行邻域比较及扩张,当模型表面种子数目达到一定数量,或模型表面种子过于密集时,则停止种子扩张过程。此时,将最终获得模型表面的纹理元素分布。
3.2 纹理元素的映射
一旦构建了三维模型表面上的纹理元素分布,即确定了待合成纹理中各纹理元素的位置,接下来的主要工作就是从给定纹理样本中提取出纹理元素,并用其替换已合成纹理元素分布中的各个种子,以获得最终的模型表面纹理合成结果。本文采用现有交互的基于图割(Graphcut)的目标对象提取方法[20]提取纹理样本中所有完整的纹理元素,仅需要对样本纹理进行简单的前景/背景标记,就能快速地提取出所有单个的纹理元素(如图5所示)。根据任一已提取出的纹理元素的面积Aref与三维模型上对应位置P,本文首先通过最短测地距离优先遍历确定待映射纹理元素在模型表面的覆盖范围R,即以位置P所在三角面片为中心,按照最短测地距离优先的方式在模型上搜索与其相邻的三角形面片。如果面片到位置P的测地距离小于r=S×Aref,则此面片在该纹理元素覆盖范围内,其中S是待映射纹理元素所对应的样本纹理元素的面积。

Fig.5 Texture elements extraction图5 纹理元素提取
在获得待映射纹理元素的局部覆盖范围R之后(如图6(a)所示),本文需要对其进行曲面局部参数化,以计算覆盖范围R内所有顶点的纹理坐标,从而将纹理元素映射至这一区域。由于除了可扩展曲面外,其他曲面上不可能存在保形映射。曲面的局部参数化会受到曲率变化的影响,特别是模型表面曲率较大部位,一般的参数化方法容易产生较大的各向异性拉伸,这样贴在三维模型表面上的纹理元素会出现参数缝隙。因此,本文根据模型各部位曲率不同自适应地在三维模型表面映射纹理元素。
在三角形网格上,以覆盖范围内三角形法线的方差近似表示覆盖范围R的曲率其中ni表示R内所有三角形的法向量,而n是其平均值。当曲率较大时(dnor>λ1,λ1是曲率阈值),直接投影对纹理元素产生较大程度的拉伸。因此,本文采用曲面参数化方法[21]以消耗更多计算量为代价,通过迭代的方式对参数化结果进行调整,以消除参数缝隙,能够有效地减少对映射后纹理元素的拉伸。当曲率较小时(dnor<λ1),为了加快合成速度,使用简单快速的直接投影对三维模型表面上所有纹理元素的覆盖区域进行参数化,即将面片投影到中心纹理元素的参考平面上;再旋转至XOY平面,缩放到(x,y)∈[(0,0),(1,1)]范围,从而映射到纹理空间。事实上,纹理元素的覆盖区域相对整个模型很小,大多数纹理元素所覆盖的区域都是较为平坦的。在这些区域内使用直接投影方法所产生的纹理拉伸、变形程度较为轻微,使得能够在保证质量的同时,快速高效地将纹理元素贴于对应的覆盖区域中。
对覆盖范围R进行参数化后,网格会产生一定程度的拉伸变形。网格拉伸程度可以由覆盖范围R内所有三角面片平均拉伸程度表示。给定任一三角形面片t参数化前后3个顶点的坐标分别为{u1,u2,u3},u∈(si,ti)和{x1,x2,x3},xi∈R3,J 是映射 A:u→x的雅克比矩阵,根据网格拉伸程度分析方法[22],其覆盖范围R内网格的拉伸程度L2可以表示为:

其中,γi和Γi是矩阵Ji的两个奇异值,分别代表三角形面片ti的局部最小和最大拉伸程度;n是覆盖范围R内三角形面片的个数。当拉伸程度过大时(L2(R)>λ2,λ2是拉伸程度阈值),使用文献[22]的方法对其重新进行参数化,即通过提高迭代次数以降低网格拉伸程度。实验表明,当λ1=0.5,λ2=1.28时,网格拉伸程度和计算开销能保持在较低水平。单个纹理元素映射结果如图6(b)所示。

Fig.6 Texture mapping图6 纹理映射示意图
4 实验结果分析与讨论
为了验证本文方法的可行性和有效性,使用多张样本纹理在多个几何模型上进行纹理合成。所有实验结果都是在CoreTMi5-4670 3.40 GHz CPU/16GB RAM的PC中进行,并采用OpenGL编程实现。

Fig.7 Experimental results comparison for algorithms图7 算法结果比较
图7给出了本文与现有4种三维模型表面纹理合成方法在合成结果上的比较,分别包括渐变纹理合成方法[6]、基于外观空间的纹理合成方法[9]、离散元素纹理合成方法[18]和基于基元分布的纹理合成方法[19]。方法[6]引入纹理元素遮片,能够很好地保存纹理元素的完整性。方法[9]使用外观向量来进行最佳匹配,但不能很好地保存样本纹理的潜在规律性。方法[18]以迭代的方法,利用能量公式对纹理元素的空间分布进行优化。但是这3种方法都需要对整个模型进行参数化来完成纹理映射。在映射过程中,受到模型表面曲率变化的影响,纹理的结构会发生变形,纹理元素的完整性也难以保证。方法[6]使用了PRAUN提出的基于块扩张的合成方法,一定程度上避免了纹理扭曲。但是由于该方法本质上还是基于像素来进行纹理合成,对顶点数量要求很高,合成的速度也较慢。方法[6]和方法[13]只能根据二维图形样本生成二维结果,再通过地图集参数化的方法映射到三维表面上,无论是纹理的结构或是纹理元素的完整性在映射过程中都无法保证。方法[19]则是直接在三维模型表面上进行合成,能在一定程度上保持样本纹理的结构规律。在将纹理元素映射到三维模型表面上对应位置的过程中,该方法使用了一种较为简单的局部参数化方法,虽然快速地获得合成结果,但是容易引起纹理元素的扭曲变形。本文方法首先直接在三维模型表面生成纹理元素的分布,以保证纹理结构的潜在规律性,再通过自适应的局部参数化方法将单个纹理元素分别贴到指定位置,从而保持纹理的完整性,以最终获得高质量的合成结果。
表2对本文方法和进行比较的方法[6]、方法[9]、方法[18]和方法[19]在纹理合成耗时上进行了统计。从表2中最后一列给出的统计数据可以看出,方法[6]合成时间与模型顶点数量相关,当模型顶点数量较大时,合成速度很慢。方法[9]能实时地合成纹理,但是需要在合成纹理前先对模型进行预处理,并使用硬件加速。直接使用方法[18]只能合成二维纹理,且相较于比较成熟的二维纹理合成方法速度较慢。而要合成三维表面纹理,还需将二维纹理映射到三维模型表面,耗时会更长。本文方法在时间效率上与方法[19]相近,但分布构建和纹理映射耗时都要更长。主要原因在于本文方法在构建分布时,为了保持样本纹理的潜在规律,反复使用邻域比较选取最佳匹配邻域,而且在纹理映射过程中使用了计算量更大的局部参数化方法以提高纹理映射的质量。需要特别说明的是,表2中的“—”表示在这一位置所对应的方法没有使用到该步骤,因而不存在对应的数据。
图8给出了使用本文方法获得的在不同三维模型上的合成结果。从中可以看出,无论纹理样本中纹理元素的分布是规则还是较为不规则,合成结果都能很好地保持其规律性。主要原因在于:本文方法能够合成与样本纹理具有外观相似的纹理元素分布。此外,通过进行局部参数化分别映射每个纹理元素,有效地保证了纹理元素的完整性。在模型中心位置,也就是用户指定的初始位置,合成纹理与样本纹理的相似度很高。然而,由于分布构建中的误差累积,随着每一次的扩张,合成纹理与样本纹理的视觉相似度逐渐降低。模型曲率变化过大也会加剧这一误差,甚至在纹理覆盖全部模型之前使合成提前终止。因此,本文方法需要在空白处手动添加纹理元素,以保证获得理想的结果。

Table 2 Running time statistics for surface textures synthesis表2 模型表面纹理合成时间统计
表3对模型表面纹理合成结果中合成的纹理元素的总数量以及总的合成时间进行了统计。从表3中可以看出,主要耗时的步骤在于三维表面上纹理元素分布的构建,其中用户给定的样本纹理会在一定程度上影响构建分布的时间。例如,样本1(图8第1列第1行)比样本2(图8第1列第2行)中的纹理元素数量多,而在模型表面上进行的分布构建所消耗的时间却更少(如表3中最后1列第1、第2行所示)。其主要原因在于样本1比样本2中的纹理元素的数量更多,分布信息更为充分,在选择最佳匹配邻域时,由于在参照二维分布中存在较多邻域可以进行选择,因而总能选取到具有最小误差的邻域,这也使得能够在纹理元素分布构建过程中有效地避免种子之间的冲突。另外,相较于分布构建的时间,纹理映射所消耗时间很少(如表3中第7列所示),且基本和纹理元素数量成正比(如表3中第5列所示)。这主要原因是,在纹理合成过程中,对大部分的纹理元素进行纹理映射的方法都是利用投影方式进行参数化的,该方法在处理不同纹理元素时所消耗的时间差别较小。

Fig.8 Experimental results for method in this paper图8 本文方法合成结果

Table 3 Number of texture elements and running time statistics for texture synthesis表3 纹理元素数量及合成时间统计
5 结束语
本文提出了一个基于分布构建的纹理合成框架,利用二维样本纹理中纹理元素的分布规律直接在三维表面生成纹理元素的分布,较好地保持了纹理结构信息。另外,通过对模型表面上纹理元素的覆盖范围分别进行局部参数化,合成的纹理元素较为完整且扭曲变形程度较低。本文方法也在一定程度上存在缺陷,当样本纹理中纹理元素分布过于密集时,三维模型表面分步构建的累积误差过大,影响了纹理结构的规律性。另外,在每一次局部扩张中反复使用邻域比较方法耗时较多,时间效率上仍有待提高。因此,如何解决以上问题也将成为本文以后探讨的主要方向。
[1]Wei Liyi,Lefebvre S,Kwatra V,et al.State of the art in examplebased texture synthesis[R].Eurographics-State of the Art Reports,Munich,Germany,2009:93-117.
[2]Zhang E,Mischaikow K,Turk G.Vector field design on surfaces[J].ACM Transactions on Graphics,2006,25(4):1294-1326.
[3]Turk G.Texture synthesis on surfaces[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques,Los Angeles,USA,Aug 12-17,2001.New York:ACM,2001:347-354.
[4]Wei Liyi,Levoy M.Texture synthesis over arbitrary manifold surfaces[C]//Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques,Los Angeles,USA,Aug 12-17,2001.New York:ACM,2001:355-360.
[5]Dischler J M,Maritaud K,Lévy B,et al.Texture particles[J].Computer Graphics Forum,2002,21(3):401-410.
[6]Zhang Jingdan,Zhou Kun,Velho L,et al.Synthesis of progressively-variant textures on arbitrary surfaces[J].ACM Transactions on Graphics,2003,22(3):295-302.
[7]Praun E,Finkelstein A,Hoppe H.Lapped textures[C]//Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques,New Orleans,USA,Jul 23-28,2000.New York:ACM,2000:465-470.
[8]Lefebvre S,Hornus S,Neyret F.Texture sprites:texture elements splatted on surfaces[C]//Proceedings of the 2005 Symposium on Interactive 3D Graphics,Washington,Apr 3-6,2005.New York:ACM,2005:163-170.
[9]Lefebvre S,Hoppe H.Appearance-space texture synthesis[J].ACM Transactions on Graphics,2006,25(3):541-548.
[10]Barla P,Breslav S,Thollot J,et al.Stroke pattern analysis and synthesis[J].Computer Graphics Forum,2006,25(3):663-671.
[11]Takashi I,Radomír M,Takeo I,et al.An example-based procedural system for element arrangement[J].Computer Graphics Forum,2008,27(2):429-436.
[12]Hurtut T,Landes P E,Thollot J,et al.Appearance-guided synthesis of element arrangements by example[C]//Proceedings of the 7th International Symposium on Non-Photorealistic Animation and Rendering,New Orleans,USA,Aug 1-2,2009.New York:ACM,2009:51-60.
[13]dos Passos V A,Walter M,Sousa M C.Sample-based synthesis of illustrative patterns[C]//Proceedings of the 18th Pacific Conference on Computer Graphics and Applications,Hangzhou,China,Sep 25-27,2010.Washington:IEEE Computer Society,2010:109-116.
[14]Gui Y,Ma L Z.Periodic pattern of texture analysis and synthesis based on texels distribution[J].The Visual Computer,2010,26(6/8):951-964.
[15]Chen Dongbin,Dong Feng.Adaptive surface texture synthesis using round-shaped neighbourhoods[J].Computer Graphics Forum,2008,27(8):2128-2142.
[16]Chen Renjie,Liu Ligang,Dong Guangchang.Local resampling for patch-based texture synthesis in vector fields[J].International Journal of Computer Applications in Technology,2010,38(1/3):124-133.
[17]Gilet G,Dischler J M.Procedural texture particles[C]//Proceedings of the 2010 Symposium on Interactive 3D Graphics,Washington,Feb 19-21,2010.NewYork:ACM,2010:6.
[18]Ma Chongyang,Wei Liyi,Tong Xin.Discrete element textures[J].ACM Transactions on Graphics,2011,30(4):62.
[19]Huang Jun,Li Feng,Gui Yan,et al.Surface texture synthesis based on texel distribution[J].Journal of Chinese Computer Systems,2016,37(10):2361-2365.
[20]Yang Nongying,Li Feng,Gui Yan.Repeated texture elements extraction from texture images[J].Journal of Frontiers of Computer Science and Technology,2015,10(8):1154-1165.
[21]Yoshizawa S,Belyaev A G,Seidel H P.A fast and simple stretch-minimizing mesh parameterization[C]//Proceedings of the 2004 International Conference on Shape Modeling and Applications,Genova,Italy,Jun 7-9,2004.Washington:IEEE Computer Society,2004:200-208.
[22]Yao Jin,Qian Guiping,Zhao Jieyi,et al.Stretch-minimizing volumetric parameterization[J].Journal of Computer Science and Technology,2015,30(3):553-564.
附中文参考文献:
[19]黄峻,李峰,桂彦,等.利用基元分布的模型表面纹理合成方法[J].小型微型计算机系统,2016,37(10):2361-2365.
[20]杨弄影,李峰,桂彦.纹理图像中重复纹理元素提取方法[J].计算机科学与探索,2015,10(8):1154-1165.

桂彦(1985—),女,湖南永州人,2012年于上海交通大学获得工学博士学位,现为长沙理工大学讲师、硕士生导师,主要研究领域为计算机图形学,计算机视觉,可视媒体编辑与处理等。

LIU Yang was born in 1990.He is an M.S.candidate at Changsha University of Science&Technology.His research interest is computer graphics.
刘杨(1990—),男,湖南长沙人,长沙理工大学计算机与通信工程学院硕士研究生,主要研究领域为计算机图形学。

LI Feng was born in 1964.He is a professor and M.S.supervisor at Changsha University of Science&Technology.His research interests include image processing,pattern recognition,computer vision and information security,etc.
李峰(1964—),男,湖南澧县人,博士,长沙理工大学教授、硕士生导师,主要研究领域为图像处理,模式识别,计算机视觉,信息安全等。
《计算机工程与应用》投稿须知
中国科学引文数据库(CSCD)来源期刊、北大中文核心期刊、中国科技核心期刊、RCCSE中国核心学术期刊、《中国学术期刊文摘》首批收录源期刊、《中国学术期刊综合评价数据库》来源期刊,被收录在《中国期刊网》、《中国学术期刊(光盘版)》、英国《科学文摘》(SA/INSPEC)、俄罗斯《文摘杂志》(AJ)、美国《剑桥科学文摘》(CSA)、美国《乌利希期刊指南》(Ulrich’s PD)、《日本科学技术振兴机构中国文献数据库》(JST)、波兰《哥白尼索引》(IC),中国计算机学会会刊
《计算机工程与应用》是由中华人民共和国中国电子科技集团公司主管,华北计算技术研究所主办的面向计算机全行业的综合性学术刊物。
办刊方针 坚持走学术与实践相结合的道路,注重理论的先进性和实用技术的广泛性,在促进学术交流的同时,推进科技成果的转化。覆盖面宽、信息量大、报道及时是本刊的服务宗旨。
报导范围 行业最新研究成果与学术领域最新发展动态;具有先进性和推广价值的工程方案;有独立和创新见解的学术报告;先进、广泛、实用的开发成果。
主要栏目 理论与研发,大数据与云计算,网络、通信与安全,模式识别与人工智能,图形图像处理,工程与应用,以及其他热门专栏。
注意事项 为保护知识产权和国家机密,在校学生投稿必须事先征得导师的同意,所有稿件应保证不涉及侵犯他人知识产权和泄密问题,否则由此引起的一切后果应由作者本人负责。
论文要求 学术研究:报道最新研究成果,以及国家重点攻关项目和基础理论研究报告。要求观点新颖,创新明确,论据充实。技术报告:有独立和创新学术见解的学术报告或先进实用的开发成果,要求有方法、观点、比较和实验分析。工程应用:方案采用的技术应具有先进性和推广价值,对科研成果转化为生产力有较大的推动作用。
投稿格式 1.采用学术论文标准格式书写,要求文笔简练、流畅,文章结构严谨完整、层次清晰(包括标题、作者、单位(含电子信箱)、摘要、关键词、基金资助情况、所有作者简介、中图分类号、正文、参考文献等,其中前6项应有中、英文)。中文标题必须限制在20字内(可采用副标题形式)。正文中的图、表必须附有图题、表题,公式要求用MathType编排。论文字数根据论文内容需要,不做严格限制,对于一般论文建议7 500字以上为宜。2.请通过网站(http://www.ceaj.org)“作者投稿系统”一栏投稿(首次投稿须注册)。
3D Surfaces Texture Synthesis Based on Elements Distribution Construction*
GUI Yan1,2,LIU Yang1,2+,LI Feng1,2
1.School of Computer&Communication Engineering,Changsha University of Science&Technology,Changsha 410114,China 2.Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation,Changsha University of Science&Technology,Changsha 410114,China
This paper proposes a novel method for surfaces texture synthesis based on elements distribution construction,in order to preserve the underlying regularity of texture samples in the synthesized texture over surfaces.This paper firstly specifies an initial position on the 3D surface by user interaction,and then expands it outward by using local growth based on neighborhood comparisons under collision detection,in order to construct the distribution of texture elements over 3D surfaces,which maintains a certain visual resemblance with the input 2D reference connectivity.According to the positions information provided by the constructed distribution of texture elements,this paper obtains the final synthesized result by pasting the extracted texture elements onto the 3D surfaces.The experimental results show that the proposed method can produce high quality textures over surfaces,which not only preserve the texture elements integrity and the underlying structural regularity well,but also guarantee low distortions and no cracks in the synthesized results.
the Ph.D.degree from Shanghai Jiaotong University in 2012.Now she is a lecturer and M.S.supervisor at Changsha University of Science&Technology.Her research interests include computer graphics,computer vision and visual media editing,etc.
2016-08, Accepted 2016-11.
A
TP391
+Corresponding author:E-mail:ly_hn@foxmail.com
GUI Yan,LIU Yang,LI Feng.3D surfaces texture synthesis based on elements distribution construction.Journal of Frontiers of Computer Science and Technology,2017,11(9):1484-1495.
10.3778/j.issn.1673-9418.1608030
*The National Natural Science Foundation of China under Grant No.61402053(国家自然科学基金);the Scientific Research Fund of Hunan Provincial Education Department under Grant Nos.16C0046,16A008(湖南省教育厅科学研究项目).
CNKI网络优先出版: 2016-11-11, http://www.cnki.net/kcms/detail/11.5602.TP.20161111.1627.010.html
Key words:surface texture synthesis;texture element distribution;neighborhood comparisons;local growth

