直觉模糊测度的计算树逻辑*
鱼先锋,李 超,李永明
1.商洛学院 数学与计算机应用学院,陕西 商洛 726000 2.陕西师范大学 计算机科学学院,西安 710062
直觉模糊测度的计算树逻辑*
鱼先锋1+,李 超1,李永明2
1.商洛学院 数学与计算机应用学院,陕西 商洛 726000 2.陕西师范大学 计算机科学学院,西安 710062
直觉模糊Kripke结构;直觉模糊测度;直觉模糊计算树逻辑;模型检测
1 引言
模型检测[1-5]作为一种形式化自动验证技术,自1981年由Clarke、Emerson等人提出之后,在计算机软硬件设计与可靠性分析、通信协议、安全协议等正确性分析方面获得了成功的应用。经典模型检测技术主要验证系统定性性质,近些年来,许多学者注重系统定量性质的验证,提出了量化模型检测技术,包括概率模型检测[6-7]、可能性模型检测[8-14]等。这些量化模型检测技术在验证不确定环境下系统量化性质方面有着各自的特点。概率模型检测用于验证系统转移在确定概率分布情况下的性质。可能性模型检测用以验证系统转移具有模糊不确定的性质,比概率模型检测表现力要强。直觉模糊集[15]是模糊集[16]的推广,可以更客观自然地表示对象间不确定的隶属关系和非隶属关系。因此研究基于直觉模糊测度的模型检测理论与技术有着重要的理论和现实意义。本文将在直觉模糊模型检测方面做些初步探索工作。
2 直觉模糊集与直觉模糊Kripke结构
定义1(intuitionistic fuzzy structure,IFS)[15]设 X是一个给定的论域,称 A={<x,μA(x),vA(x)>|x∈X}为 X上的IFS,其中,μA(x):X→I,vA(x):X→I,且 0≤μA(x)+vA(x)≤1(∀x∈X)。 μA(x)表示 x对 A的隶属程度,vA(x)表示x对A的非隶属程度。X上的所有IFS记为IFS(x)。称πA(x)=1-μA(x)-vA(x)为x对 A的犹豫度。X中x对A的隶属度与非隶属度所组成序对(μA(x),vA(x))称为直觉模糊数。因此,可以将X上的IFSA看作直觉模糊数的集合,即可记A={(μA(x),vA(x))|x∈X}。
定义2(直觉模糊关系的合成)[17]设 P=(μPij,γPij)n×n和 Q=(μQij,γQij)n×n为直觉模糊矩阵,若 R=P∘Q=(μij,γij)n×n,则称R是P和Q的合成矩阵,这里
定义3(直觉模糊数的序)对任意两个直觉模糊数 a=(μ1,λ1),b=(μ2,λ2) ,,若 μ1=μ2且λ1=λ2,则称直觉模糊数a等于b,记作a=b;否则:
(1)若d>0,则称a大于b,记作a>b;
(2)若d<0,则称a小于b,记作a<b。
若 μ1=μ2且 λ1=λ2,则称直觉模糊数a等于b是很自然的。若 μ1>μ2,λ1≤λ2,此时 a>b也是自然的,但若出现 μ1>μ2,λ1>λ2这种情况,就不好刻画 a 与 b的大小了。比如,a=(0.8,0.1),b=(0.7,0.05)。这种情况下考虑隶属度比值与非隶属度比值的差异情况,即即d>0,说明隶属度的差异较大,对直觉模糊数的大小区别做主要贡献,故认为a>b是合理的。同理定义3中关于a<b的定义也是合理的。
定义 4(intuitionistic fuzzy Kripke structure,IFKS)一个直觉模糊Kripke结构(IFKS)是一个五元组,表示为M=(S,P,I,AP,L),其中:
(1)S是一个可数非空状态集合。
(2)P:S×S→[0,1]2是直觉模糊转移函数,满足对于每个状态s都有成立;一般的∀s,s′∈S,P(s,s′)=(μ,γ),这里 (μ,γ)∈[0,1]2是一个直觉模糊数。其中 μ刻画了从状态s迁移到状态s′的可达度,γ刻画了从状态s迁移到状态s′的不可达度,π=1-μ-γ刻画了从状态s迁移到状态s′的犹豫程度。
(3)I:S→[0,1]2是初始可能性分配函数,使得
(4)AP是一组原子命题之集。
(5)L:S→2AP是标记函数,即在每个状态下都有一个赋值(AP的子集)。
如果S和AP是有穷的,则称M为有穷的直觉模糊Kripke结构。
注意1这里假设 AP=S和L(s)={s},对X⊆[0,1],集合X的最小上界和最大下界分别用∨X和∧X表示。所有满足I(s)>0的状态s被定义为初始状态。对于状态s和T⊆S,P(s,T)表示从状态s出发经过一步转移到达T中的某些状态t的可达度,表示为。
例1如图1所示为一个IFKSM=(S,P,I,AP,L)的图形表示,图中圆圈代表状态,箭头代表转移,箭头上的数字表示一个状态转移到另一个状态的可达度。其中 S={s0,s1,s2,s3},I(s0)=(1,0),即初始状态是 s0,L(s0)={s0},L(s1)={s1},L(s2)={s2},L(s3)={s3},P(s0,s1)=(1,0),P(s0,s2)=(0.2,0.6),P(s1,s2)=(1,0),P(s1,s3)=(0.9,0.06),P(s2,s1)=(0.7,0.1),P(s2,s3)=(1,0),P(s3,s3)=(1,0)。通常用矩阵(P(s,t))s,t∈S表示直觉模糊转移函数P:S×S→[0,1]2,称其为直觉模糊转移矩阵。该IFKS的直觉模糊转移矩阵为(按顺序 s0<s1<s2<s3表示第1、2、3、4行和列):


Fig.1 IFKS M has 4 states图1 四状态的IFKS M
对于IFKSM,无穷状态序列π=s0s1s2…∈Sw表示M中的无穷路径,其中对于所有的i∈N,满足P(si,si+1)>0。用Paths(M)表示M中无穷路径集合。Pathsfin(M)表示M中所有有穷路径集合,有穷路径形如 s0s1…sn(n∈N),对于 0≤i<n,P(si,si+1)>(0,1)。Paths(s)表示M中从状态s出发的无穷路径集合。Pathsfin(s)表示M中从状态s出发的有穷路径集合,形如s0s1…sn,其中 s0=s。
M中的状态和状态集合的前驱(记为Pre)、后继(记为Post)的定义如下:

3 直觉模糊Kripke结构上的直觉模糊测度


实际上,上述直觉模糊测度满足以下定理2的3个条件,从而称IFPM为Ω上的直觉模糊测度是合理的。另外,在不发生歧义的情况下,IFPM简写为IFP。
定理1设M是一个IFKS,则有穷路径扩展的无穷路径的直觉模糊测度表示为:

特别地,

证明 因为Cyl(s0s1…sn)=⋃{π∈Sw|s0s1…sn∈Pref(π)},则有 IFP(Cyl(s0s1…sn))=∨{Po(π)|s0s1…sn∈Pref(π)}=


在文章后续,用IFP(s0s1…sn)来表示。
定理2直觉模糊测度IFP满足以下3个性质:
(1)IFP(∅)=(0,1),IFP(Paths(M))=(1,0);
(2)如果 Ai∈Ω ,i∈N ,则;
(3)如果 A⊆B,A,B∈Ω,则IFP(A)≤IFP(B)。但一般的,下列性质未必是成立的:
(4)如果 A1⊇A2⊇…为下降列,则
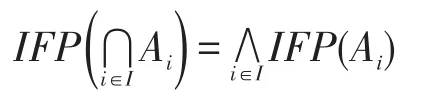
证明 (1)①因为 IFP(∅)= ∨{IFP(π)|π∈∅}=(0,1),所以 IFP(∅)=(0,1)。),所以 IFP,根据定理1可知 IFP(Paths(M))=。又因为对于,所以 IFP(Paths(M))=(1,0)。
(2)因为

所以性质(2)成立。
(3)因为 A⊆B,根据性质(2)可得:

进而推出IFP(A)≤IFP(B)。


Fig.2 IFKSMhas 2 states图2 二状态的IFKS M
定义7M=(S,P,I,AP,L)为IFKS,P是关于状态s的直觉模糊传递分布。∀s∈S,T⊆S,P(s,T)表示经s一步转移至T的直觉模糊测度,即∀s,t∈S,P的传递闭包P+定义为:

注意2∀s,t∈S,在IFKSM=(S,P,I,AP,L)中必然存在有穷路径使得其中s0=s,sn=t。因此P的传递闭包P+还可以表示成。其中 Pk+1=Pk∘P ,这里∘为定义2给出的直觉模糊矩阵合成运算,即maxmin复合运算。
下面引入函数r(s)方便描述本文后续结果。
定义8 M=(S,P,I,AP,L)为IFKS,r:S→[0,1]2,∀s∈
下面给出r(s)的一种形式化计算方法。
定理3 M=(S,P,I,AP,L)为IFKS,假设 n=|S|是有穷的,则∀s∈S,有:

证明 分两步证明:

(2)因为 P+(s,t)∧P+(t,t)=P(s1,s2)∧…∧P(si,t)∧P(t,t1)∧P(t1,t2)∧…∧P(tr,t),其中 s1=s,si,t,tr∈S,i,r∈N,所以对M中的任一无穷路径π+=s1s2…si(tt1…trt)ω,有:

由π+的任意性可得,
综合(1)、(2)知定理3成立。 □
注意3定理3计算r(s)的时间主要取决于计算直觉模糊关系矩阵P的传递闭包P+,所以时间复杂度为O(n2lbn)[18]。
4 直觉模糊计算树逻辑及其性质
直觉模糊计算树逻辑(intuitionistic fuzzy computation tree logic,IFPCTL)是建立在IFKS上的一种计算树逻辑。和经典计算树逻辑(computation tree logic,CTL)公式一样,IFPCTL公式也包含状态公式和路径公式。不同的是IFPCTL不再使用路径量词∃、∀,而用 IFPJ(φ)代替。这里 φ 是路径公式,J⊆[0,1]2,J表示公式φ的直觉模糊上界和下界。∀s∈IFKS M,s╞IFPJ(φ)表明IFP(Paths(s))⊆J。定量性是指到达坏状态的IFP足够小,或者到达好状态的IFP很大,超过给定值。定性性是定量性的一个特例,它要求所有转移的IFP不是(0,1)就是(1,0)。
定义9定量的IFPCTL语构定义如下。
IFPCTL的状态公式:

其中,a∈AP;ϕ、ϕ1、ϕ2是IFPCTL状态公式;φ是IFPCTL路径公式;J⊆[0,1]2。 IFP≤(0.5,0.25)(φ)表示IFP[(0,1),(0.5,0.25)](φ)。
IFPCTL的路径公式:

其中 ϕ、ϕ1、ϕ2是IFPCTL状态公式,n∈N 。
定义10M=(S,P,I,AP,L)为IFKS,∀s∈S,a∈AP,ϕ1、ϕ2是IFPCTL状态公式,φ是IFPCTL路径公式,则IFPCTL满足的关系为:
(1)s╞IFPJ(φ)当且仅当IFP(s╞φ)∈J,其中IFP(s╞φ)=IFP({π∈Path(s)|π╞φ});
(2)π╞ϕ1⋃≤nϕ2当且仅当∃0≤j≤n,π[j]╞ϕ2且∀0≤k<j,π[k]╞ϕ1。
特别的:
(1)π╞⋄ϕ当且仅当∃j≥0,π[j]╞ϕ;
(2)π╞□ϕ当且仅当∀j≥0,π[j]╞ϕ;
(3)π╞ϕ1Wϕ2当且仅当 π╞ϕ1⋃ϕ2或 π╞□ϕ1。
其他满足关系与经典的CTL公式满足关系相同,详见文献[19]。
定义11 ϕ、ψ为IFPCTL状态公式,记Sat(ϕ)={s|s∈S,s╞ϕ},称ϕ与ψ等价,记作ϕ≡ψ,当且仅当Sat(ϕ)=Sat(ψ)。
定理 4 IFP>(0,1)(○IFP>(0,1)(⋄ϕ))≡ IFP>(0,1)(⋄IFP>(0,1)(○ϕ))。
证明 先证 Sat(IFP>(0,1)(○IFP>(0,1)(⋄ϕ)))⊆Sat(IFP>(0,1)(⋄IFP>(0,1)(○ϕ))),∀s∈ Sat(IFP>(0,1)(○IFP>(0,1)(⋄ϕ))),即:

则s有直接后继顶点t0,满足t0╞IFP>(0,1)(⋄ϕ)。这样就存在从 t0出发,到达 tn∈Sat(ϕ)的路径 t0t1…tn。其中,tn-1╞IFP>(0,1)(○ϕ),这样就得到路径st0t1…tn-1,满足s╞IFP>(0,1)(⋄IFP>(0,1)(○ϕ))。因此,s∈Sat(IFP>(0,1)(⋄ IFP>(0,1)(○ϕ))),也就有:

再 证 Sat(IFP>(0,1)(⋄ IFP>(0,1)(○ϕ)))⊆ Sat(IFP>(0,1)(○IFP>(0,1)(⋄ϕ))),∀s∈Sat(IFP>(0,1)(⋄IFP>(0,1)(○ϕ))),即:

则存在路径s0s1…sn,其中s=s0,sn╞IFP>(0,1)(○ϕ)。这样sn必有一直接后继t,且t╞ϕ。这样就得到路径s1s2…snt使得s1╞IFP>(0,1)(⋄ϕ),由于s1为s0的一个后继,故有s╞IFP>(0,1)(○IFP>(0,1)(⋄ϕ))。因此,s∈Sat(IFP>(0,1)(○IFP>(0,1)(⋄ ϕ))),也就有:

综上 Sat(IFP>(0,1)(○IFP>(0,1)(⋄ϕ)))=
Sat(IFP>(0,1)(⋄ IFP>(0,1)(○ϕ)))
由定义10知:
IFP>(0,1)(○IFP>(0,1)(⋄ ϕ))≡IFP>(0,1)(⋄IFP>(0,1)(○ϕ)) □
定义12定性的IFPCTL的语构递归定义如下。
IFPCTL的状态公式:
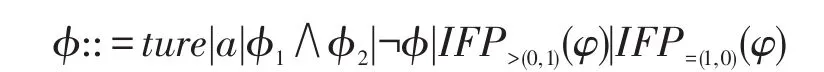
其中,a∈AP;ϕ、ϕ1、ϕ2是IFPCTL状态公式;φ是IFPCTL路径公式。
IFPCTL的路径公式:

其中ϕ、ϕ1、ϕ2是IFPCTL状态公式,n∈N。
定义13 ϕ、ψ为IFPCTL或PoCTL(possibilistic computation tree logic)或CTL,称 ϕ 等价于 ψ ,记作 ϕ≡ψ,当且仅当 Sat(ϕ)=Sat(ψ)。
注意4定义12指出若满足给定的IFPCTL,PoCTL和CTL的状态之集相同,就可以称所满足的公式是等价的,这使得IFKS、PoKS和KS间的模拟刻画成为可能。
定理5以下IFPCTL、PoCTL和CTL公式等价:
(1)IFP>(0,1)(⋄a)≡PO>0(⋄a)≡∃⋄a
(2)IFP>(0,1)(○a)≡ PO>0(○a)≡ ∃○a
(3)IFP>(0,1)(□a)≡ PO>0(□a)≡∃□a
(4)IFP>(0,1)(a⋃b)≡PO>0(a⋃b)≡∃(a⋃b)
(5)IFP>(0,1)(aWb)≡PO>0(aWb)≡∃(aWb)
证明(1)先证IFP>(0,1)(⋄a)≡∃⋄a。设s╞IFP>(0,1)(⋄a),则IFP(s╞⋄a)>(0,1)。因此{π|π∈Path(s),π╞⋄a}≠∅,故s╞∃⋄a。另一方面设s╞∃⋄a,则存在路径s0s1…si…,其中s=s0且∃si使得si╞a。因此IFP(s╞⋄a)≥IFP((s0s1…si…)╞⋄a)>(0,1),从而s╞IFP>(0,1)(⋄a)。综 上 IFP>(0,1)(⋄a)≡∃⋄a 。再 证 PO>0(⋄a)≡∃⋄a,与 IFP>(0,1)(⋄a)≡∃⋄a的证明方法一样,不再累述。所以 IFP>(0,1)(⋄a)≡PO>0(⋄a)≡∃⋄a。
(2)、(3)的证明与(1)类似。
(4)先证明IFP>(0,1)(a⋃b)≡∃(a⋃b)。假设s╞IFP>(0,1)(a⋃b),则IFP(s╞(a⋃b))>(0,1)。因此{π|π∈Path(s),π╞(a⋃b)}≠∅,故s╞∃(a⋃b)。另一方面设s╞∃(a⋃b),则存在有穷路径s0s1…sn,其中s=s0且si╞a(i=0,1,…,n-1),sn╞b。因此IFP(s╞(a⋃b))≥IFP((s0s1…sn)╞(a⋃b))>(0,1),从而s╞IFP>(0,1)(a⋃b)。综上IFP>(0,1)(a⋃b)≡∃(a⋃b)。再证 PO>0(a⋃b)≡∃(a⋃b),与 IFP>(0,1)(a⋃b)≡∃(a⋃b)的证明方法一样,不再累述。因此IFP>(0,1)(a⋃b)≡PO>0(a⋃b)≡∃(a⋃b)。
(5)先证明IFP>(0,1)(aWb)≡∃(aWb)。假设s╞IFP>(0,1)(aWb),则IFP(s╞(aWb))>(0,1)。因此{π|π∈Path(s),π╞(aWb)}≠∅,故s╞∃(aWb)。假设s╞∃(aWb),则存在有穷路径s0s1…sn,其中s=s0且si╞a(i=0,1,…,n-1),sn╞b;或存在路径s0′s1′…,其中s′=s0′且∀i≥0,si′╞a。因此IFP(s╞(aWb))≥IFP(s0s1…sn)∨IFP(s0′s1′…)>(0,1),从而s╞IFP>(0,1)(aWb)。综上IFP>(0,1)(aWb)≡∃(aWb)。再证 PO>0(aWb)≡∃(aWb),与 IFP>(0,1)(aWb)≡∃(aWb)的证明方法一样,不再累述。 □
定理6以下IFPCTL和PoCTL公式等价:
(1)IFP=(1,0)(⋄ a)≡ PO=1(⋄ a)
(2)IFP=(1,0)(□a)≡ PO=1(□a)
(3)IFP=(1,0)(○a)≡ PO=1(○a)
(4)IFP=(1,0)(a⋃b)≡PO=1(a⋃b)
(5)IFP=(1,0)(aWb)≡ PO=1(aWb)
直觉模糊测度的非隶属度为“0”,它就退化成对应的可能测度了,因此定理6成立是显然的。
定理7以下IFPCTL和CTL公式不等价:
(1)IFP=(1,0)(⋄a)≢∀⋄a
(2)IFP=(1,0)(□a)≢∀□a
(3)IFP=(1,0)(○a)≢∀○a
(4)IFP=(1,0)(a⋃b)≢∀(a⋃b)
(5)IFP=(1,0)(aWb)≢∀(aWb)
假设ϕ既是IFPCTL也是CTL,则Sat(IFP=(1,0)(ϕ))={s|s∈S,IFP(path(s))=(1,0)},考虑 s∈Sat(IFP=(1,0)(ϕ)),存在从 s出发的路径 s10s11…,s20s21…,…sk0sk2…,其中s=s10=s20=…=sk0,k∈N。因为(si0si1…╞ϕ),所以 s∈Sat(IFP=(1,0)(ϕ)),必须且只需∃0≤i≤k,使得 IFP(si0si1…╞ϕ)=(1,0)。而 s∈Sat(∀ϕ)要求∀0≤i≤k,使得 IFP(si0si1…╞ϕ)=(1,0),显然 Sat(∀ϕ)⊆Sat(IFP=(1,0)(ϕ))。
因此一般情况下IFP=(1,0)(ϕ)≡∀ϕ。对于定理7中的结论很容易给出反例来证明它们。
5 小结
本文建立了IFKS模型(定义4),提出了直觉模糊测度空间理论(定义6),讨论了IFKS的一系列性质(定理1、定理2)。定义了IFKS中任一路径的直觉模糊测度以及从任一状态出发的路径簇的直觉模糊测度。提出了路径转移矩阵P及其传递闭包P+的概念(定义7),给出了通过计算路径转移矩阵传递闭包计算路径IFP的算法(定理3),分析了算法的复杂度。提出了直觉模糊计算树逻辑(IFPCTL)理论(定义9、定义13),讨论了一组IFPCTL、PoCTL和CTL公式的等价性(定理4、定理5)。给出了一组等价的IFPCTL和PoCTL公式(定理6),以及一组不等价的IFPCTL和CTL公式(定理7)。这些性质是IFPCTL、PoCTL和CTL模拟刻画的基础,也是直觉模糊测度模型检测的基础。
[1]Clake E,Grumberg O,Peled D.Model checking[M].Cambridge,USA:MIT Press,1999.
[2]Lin Huimin,Zhang Wenhui.Model checking:theories,techniques and applications[J].Acta Electronica Sinica,2002,30(12A):1907-1912.
[3]Baier C,Katoen J P.Principles of model checking[M].Cambridge,USA:MIT Press,2007.
[4]Rozier K Y.Linear temporal logic symbolic model checking[J].Computer Science Review,2011,5(2):163-203.
[5]Yu Xianfeng,Lei Lihui,Li Yongming.Modeling and verification of batch system[J].Computer Science,2011,38(4):257-259.
[6]Hart S,Sharir M.Probabilistic propositional temporal logics[J].Information and Control,1986,70(2/3):97-155.
[7]Hansson H.Time and probability in formal design of distributed systems[M].New York:Elsevier Science Inc,1994.
[8]Xue Yan,Lei Hongxuan,Li Yongming.Computation tree logic based on possibility measure[J].Computer Engineering and Science,2011,33(9):70-75.
[9]Xue Yan,Lei Hongxuan,Li Yongming.Possibilistic Kripke structure decision processes[C]//Proceedings of the 2012 Conference on Quantitative Logic and Soft Computing,Xi'an,China,May 12-15,2012.Singapore:World Scientific Publishing Company,2012:295-302.
[10]Li Yongming,Li Lijun.Model-checking of linear-time properties based on possibility measure[J].IEEE Transactions on Fuzzy Systems,2013,21(5):842-854.
[11]Deng Hui,Xue Yan,Li Yali,et al.Computation tree logic CTL*based on possibility measure and possibilistic bisimulation[J].Computer Science,2012,39(10):258-263.
[12]Li Yali,Li Yongming.Some properties of computation tree logic under possibility measure[J].Journal of Shaanxi Normal University:Natural Science Edition,2013,41(6):6-11.
[13]Li Yongming.Two methods for possibilistic linear temporal logic model checking[J].Journal of Shaanxi Normal University:Natural Science Edition,2014,42(6):21-25.
[14]Ma Zhanyou,Li Yongming.Model checking of reachability problem based on possibility measure[J].Fuzzy Systems and Mathematics,2014,28(6):88-97.
[15]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and System,1986,20(1):87-96.
[16]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[17]Zhao Faxin,Ma Zongmin,Yan Li.Fuzzy clustering based on vague relations[C]//LNCS 4223:Proceedings of the 3rd International Conference on Fuzzy Systems and Knowledge Discovery,Xi'an,China,Sep 24-28,2006.Berlin,Heidelberg:Springer,2006:79-88.
[18]Garmendia L,González R C,López V,et al.An algorithmto compute the transitive closure,a transitive approximation and a transitive opening of a fuzzy proximity[J].Mathware and Soft Computing,2009,16(2):175-191.
[19]Baier C,Katoen J P.Principles of model checking[M].Cambridge,USA:MIT Press,2007.
附中文参考文献:
[2]林惠民,张文辉.模型检测:理论、方法与应用[J].电子学报,2002,30(12A):1907-1912.
[5]鱼先锋,雷丽晖,李永明.单道批处理系统的建模与验证[J].计算机科学,2011,38(4):257-259.
[8]薛艳,雷红轩,李永明.基于可能性测度的计算树逻辑[J].计算机工程与科学,2011,33(9):70-75.
[11]邓辉,薛艳,李亚利,等.基于可能性测度的计算树逻辑CTL*与可能性互模拟[J].计算机科学,2012,39(10):258-263.
[12]李亚利,李永明.可能性测度下计算树逻辑的若干性质[J].陕西师范大学学报:自然科学版,2013,41(6):6-11.
[13]李永明.可能LTL模型检测的两种方法[J].陕西师范大学学报:自然科学版,2014,42(6):21-25.
[14]马占有,李永明.基于广义可能性测度的可达性问题的模型检测[J].模糊系统与数学,2014,28(6):88-97.

YU Xianfeng was born in 1984.He is an M.S.candidate and lecturer at Shangluo University.His research interest includes model checking and fuzzy system analysis,etc.
鱼先锋(1984—),男,陕西商州人,商洛学院硕士研究生、讲师,主要研究领域为模型检测,模糊系统分析等。

LI Chao was born in 1965.He is a professor at Shangluo University.His research interest includes model checking and fuzzy system analysis,etc.
李超(1965—),男,陕西镇安人,商洛学院教授,主要研究领域为模型检测,模糊系统分析等。
Computation Tree Logic Based on Intuitionistic Fuzzy Measure*
YU Xianfeng1+,LI Chao1,LI Yongming2
1.Institute of Mathematics and ComputerApplication,Shangluo University,Shangluo,Shaanxi 726000,China 2.School of Computer Science,Shaanxi Normal University,Xi'an 710062,China
This paper establishes the intuitionistic fuzzy Kripke structure(IFKS)model,proposes the intuitionistic fuzzy measure theory based on IFKS,and expounds a series of properties of IFKS.Then,this paper proves that the intuitionistic fuzzy probability(IFP)of every path in an IFKS is the infimum of the IFP of the initial state and every translation in the path,and the IFP of those paths that start from the same initial state is the supremum of their IFP.This paper also defines the transfer matrix of pathPand its transitive closureP+,gives an algorithm which can be used for calculatingP+,and analyzes the complexity of the algorithm.After that,this paper builds the intuitionistic fuzzy computation tree logic(IFPCTL)theory,and discusses the equivalence of a set of formula about IFPCTL,possibilistic computation tree logic(PoCTL)and computation tree logic(CTL).Finally,this paper gives a set of equivalent formula about IFPCTL and PoCTL,and a set of inequitable formula about IFPCTL and CTL at the same time.
intuitionistic fuzzy Kripke structure;intuitionistic fuzzy probability;intuitionistic fuzzy computation tree logic;model checking
the Ph.D.degree from Sichuan University in 1996.Now he is a professor and Ph.D.supervisor at Shaanxi Normal University,and the senior member of CCF.His research interests include intelligent computing,fuzzy system analysis,quantum information and quantum logic,etc.
2016-06, Accepted 2016-08.

A
TP301.2
+Corresponding author:E-mail:pioneer.369@163.com
YU Xianfeng,LI Chao,LI Yongming.Computation tree logic based on intuitionistic fuzzy measure.Journal of Frontiers of Computer Science and Technology,2017,11(9):1523-1530.
10.3778/j.issn.1673-9418.1606020
*The National Natural Science Foundation of China under Grant No.61228305(国家自然科学基金);the Special Research Foundation of Department of Education of Shaanxi Province under Grant No.2015JK0605(陕西省教育厅专项科研计划项目);the Science Foundation of Shangluo University under Grant No.15SKY001(商洛学院科研项目).
CNKI网络优先出版: 2016-08-19, http://www.cnki.net/kcms/detail/11.5602.TP.20160819.0932.002.html
摘 要:建立了直觉模糊Kripke结构(intuitionistic fuzzy Kripke structure,IFKS)模型,提出了基于直觉模糊Kripke结构的直觉模糊测度空间理论,阐述了IFKS的一系列性质。证明了任一路径转移的直觉模糊可达度(intuitionistic fuzzy probability,IFP)为初始状态的直觉模糊测度与各转移的IFP所取下确界,任一状态出发的所有路径上路径转移的IFP为所有路径可达度的上确界。给出了路径转移矩阵P及其传递闭包P+的概念,给出了通过计算路径转移矩阵传递闭包,计算路径可达度的算法,并分析了算法的复杂度。提出了直觉模糊计算树逻辑(intuitionistic fuzzy computation tree logic,IFPCTL)理论,讨论了一组IFPCTL、可能测度计算树逻辑(possibilistic computation tree logic,PoCTL)和经典计算树逻辑(computation tree logic,CTL)公式的等价性。最后给出了一组等价的IFPCTL和PoCTL公式以及一组不等价的IFPCTL和CTL公式。
李永明(1966—),男,陕西大荔人,1996年于四川大学获得博士学位,1999年于西北工业大学博士后流动站出站,现为陕西师范大学教授、博士生导师,CCF高级会员,主要研究领域为计算智能,模糊系统分析,量子计算与量子逻辑等。

