模糊保险箱算法的模板校准参数优化研究*

张 璐，王金海，崔 军，赵军发，陈泓宇

天津工业大学 电子与信息工程学院，天津 300387

模糊保险箱算法的模板校准参数优化研究*

张 璐，王金海，崔 军+，赵军发，陈泓宇

天津工业大学 电子与信息工程学院，天津 300387

在模糊保险箱（fuzzy vault）算法的具体实现中，几何哈希法是一种用于生物特征模板自动校准的常见技术。针对算法实现时的参数取值模糊问题，研究了影响Fuzzy Vault模板匹配精度的3个参数：图片像素大小、哈希表基点数和哈希表量化参数（α和β）。通过设计单因素实验方法，得到了这3个参数的最优取值范围，并改进了Fuzzy Vault算法细节点的提取范围和基点距离的选取规则，最后基于FVC指纹数据库对算法优化前后的匹配精度进行对比实验。结果表明，优化后算法的拒真率（false rejection rate，FRR）至少降低了9.84%，认假率（false acceptance rate，FAR）至少降低了7.12%，说明该优化方案提高了算法的匹配精度，具有一定的鲁棒性和实用性。

模糊保险箱；生物特征；几何哈希法；自动校准；指纹

1 引言

当今，信息化高速发展，身份认证被广泛应用于各个场景。生物特征识别技术将用户的数字身份与物理身份进行有效统一而备受关注。但是生物特征所具有的唯一性、不可撤销性等特点，导致信息一旦丢失，将再也无法恢复使用。因此，为保障生物特征信息的安全，生物特征加密（biometric encryption，BE）技术应运而生。生物特征加密最早由Tomko[1]在1994年提出。这种技术最为经典的算法是模糊保险箱（fuzzy vault）[2]，该算法的最大优势是把生物特征的模糊性和密码的精确性良好地结合起来。此后，Clancy等人[3]提出了Fingerprint Vault的概念，实现了基于指纹的加密库。Uludag等人[4]提出了Fuzzy Vault for Fingerprint算法，这种算法更为实用和安全。此后，许多文献对指纹模糊保险箱进行了改进，Moon等人[5]用一种自适应的多项式阶数表示用户的细节提取数量。文献[6]通过增加细节点的方向信息，增强了指纹模糊保险箱的精度与安全性。谭台哲等人[7]解决了指纹Fuzzy Vault中密钥长度决定解码时需要匹配细节点个数的问题，使算法更加灵活。文献[8]建立了一种基于细节点成对结构的指纹模糊保险箱。Malkauthekar[9]采用两个多项式对细节点进行加密。Moon等人[10]分析了模糊保险箱在智能卡上的实际应用。此外，模糊保险箱还被应用到其他生物特征识别中。Lee等人[11]提出了基于虹膜图像的模糊金库。然后，Sowkarthika等人[12]提出了虹膜与指纹融合的模糊金库，识别结果更为准确。Wu等人[13]提出了基于掌纹的密码系统。2015年，又有学者提出了精度更高的两种混合可撤除掌纹密码系统[14]。基于人脸的模糊保险箱算法也由Wu等人[15]最早提出。另外，Eskander等人[16]提出了一种基于离线签名图像的Fuzzy Vault系统。本文算法参数优化的研究对象为指纹模糊保险箱算法。

模糊保险箱算法中的一个难点是模板校准问题。由于采集指纹时会发生形变（移动、旋转、缩放），对应点的坐标值相应改变，导致在模糊保险箱解密阶段，注册模板与验证模板进行对比时，无法识别真实细节点，从而影响精确度。如果不进行模板校准，模糊保险箱仅能识别同一张指纹图片，在实际应用中就无法完成用户的身份认证。Yang等人[17]通过在极坐标中找到一组新的特征集来进行校准。Nandakumar等人[18]提出了基于辅助数据的配准方法。2010年，出现了一种免配准模糊保险箱算法，它基于细节描述符[19]和细节局部结构[20]，并且用SHA-2（secure hash algorithm 2）替代了循环冗余校验（cyclic redundancy check，CRC）编码[21]。后来，Nasiri等人[22]提出了另一种免校准方法，在注册阶段由一个指纹模板生成多个模糊保险箱库，在验证阶段只要有两个库解码成功即可恢复密钥。此外，又有学者提出在指纹的核心处构建一个局部定位模型的方法进行校准[23]。Yang等人[24]用一种Delaunay四边形的方法对指纹图片进行配准。文献[25]提出一种基于指纹细节点频谱的指纹匹配算法，利用傅里叶-梅林变换进行指纹模板的校准。Chung等人[26]提出一种基于几何哈希表的配准方法。Moon等人[27]在此基础上进行了实验分析，并得到了一系列的实验数据。文献[28-29]也应用几何哈希法对指纹模板进行校准，并指出该方法的研究价值。几何哈希法是根据几何特征编码形成一个可以存储大量信息的哈希表，哈希表中仅存储细节点的相对位置信息，保护了用户的隐私，因此广泛应用于加密域中的校准问题。但现有文献都没有明确指出参数的具体取值问题，导致在应用过程中匹配精度不高和实验重现困难。

本研究在实现基于几何哈希自动校准技术的模糊保险箱算法平台的基础上，实验分析图片像素大小、哈希表基点数以及哈希表量化参数（α和 β）对匹配精度的影响，得到参数的最优取值范围，并优化细节点提取和基点选取规则，最终提高了算法的匹配精度。

2 指纹模糊保险箱基础知识

模糊保险箱算法的安全性是基于多项式重构问题的，并且该算法的处理对象是无序集合。因此，该算法特别适用于生物特征数据，例如指纹的细节点[30]。

2.1 指纹模糊保险箱算法

指纹Fuzzy Vault算法是在Fuzzy Vault的基础上实现的更为实用化的一种算法。该算法通过指纹信息达到了个人身份特征与密钥信息相互绑定的目的。该算法的基本原理是：加密时，首先通过CRC对密钥进行编码，然后将其作为多项式的系数构造多项式函数，注册用户将生物特征信息映射到多项式曲线上，而后随机地添加杂凑点形成完整的集合作为模板存储在保险箱中（如图1所示）；解密时，从验证用户中提取细节信息先进行校准，然后与加密模板对比，当解密模板提供足够多与加密模板相近的特征信息时，即可确定为真实的解锁集合，并通过多项式重构获得密钥信息，最后再使用CRC来确定真实的密钥（如图2所示）。

该算法的具体实现过程通过一个例子体现。

为简单说明，多项式阶数设定为2阶，即P=ax2+bx+c，细节点个数设为4，即 L={mi=(xi,yi,θi,ti)|1≤i≤ 4}，杂凑点个数为 2，即 B={ci=(xi′,yi′,θi′,ti′)|1 ≤ i≤2}。其中x、y表示细节点的坐标值；θ表示细节点的方向场值；t表示细节点的类型（端点、分叉点等）。

（1）注册阶段

①利用随机数生成器生成32 bit随机数作为密钥K={a,b}，通过CRC编码为KC={a,b,c}。

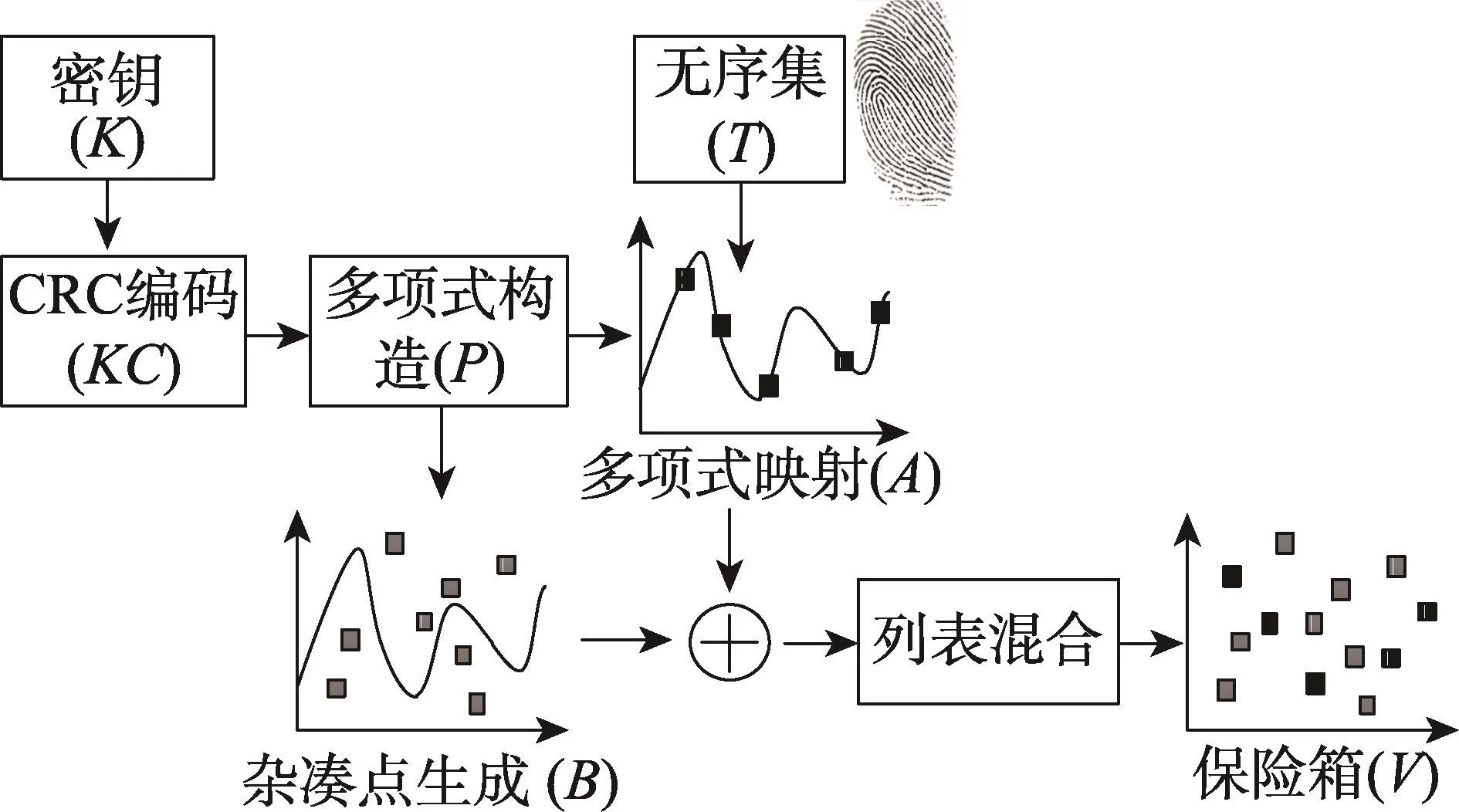
Fig.1 Encryption of fuzzy vault for fingerprint图1 指纹模糊保险箱加密

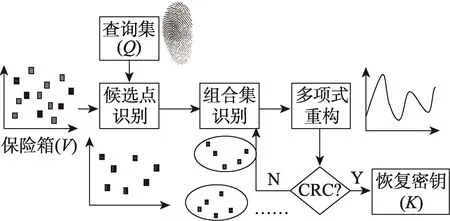
Fig.2 Decryption of fuzzy vault for fingerprint图2 指纹模糊保险箱解密

②将KC中的值转换到有限域GF（216）中，作为多项式各项的系数，构造多项式为P=ax2+bx+c。

③提取出细节点集的坐标L={mi=(xi,yi)|1≤i≤4}，级联 x和 y，即 x|y ，再转换到GF（216）域中，计算x|y在多项式P上的投影点，得到A={ti=(xi|yi,P(xi|yi))|1≤i≤4}，再加入随机生成的杂凑点集 B′={ti′=(xi′|yi′,∉ P(xi′|yi′))|1 ≤ i≤ 2}，最终将投影点与杂凑点组合，形成模糊保险箱 V=A⋃ B′={t1,t2,t3,t4,t1′,t2′}存储起来，注册阶段结束。

（2）验证阶段

①从验证用户中提取细节点集Q，将注册模板与验证模板进行校准，找出待解密的真实细节点集L′={mi=(xi,yi)|1≤i≤n}（具体过程在2.2节中介绍）。

②根据真实细节点集L′，在模糊保险箱V中找到对应多项式点集 A′={ti=(xi|yi,P(xi|yi))}的值，如果多项式点集A′中的元素个数大于或等于多项式系数的个数，即可以通过Lagrange插值法重构出多项式P，因此本例中至少能找到t1、t2、t3、t4中的任意3个多项式点才能重构多项式P，得到系数a、b、c。

③利用CRC判断是否为原始多项式系数KC={a,b,c}，如果校验结果为0，则匹配成功，释放密钥K={a,b}，否则，无法释放密钥K。至此，验证阶段结束。

对于细节点提取个数的选取，文献[30]基于安全性和计算复杂度两方面的考虑，对指纹细节点进行过滤，选取了最可靠的20个细节点作为模板特征，因为太多的细节点会使多项式构建变得极为复杂，严重影响加解密的效率。

2.2 几何哈希自动校准技术

几何哈希技术是一种有效的模型识别方法，由经过任意变换的点集合和线性近似的曲线集合组成的具有几何特征的物体，运用几何特征的最小编码物体的几何关系进行识别[31]。由于几何哈希法具有鲁棒性、高效率和低多项式复杂度等特点，得到了广泛应用[29]。该算法应用于Fuzzy Vault的基本原理是：在模糊保险箱的注册阶段，对提取出的细节点进行几何哈希变换生成注册哈希表（如图3所示）；验证阶段，通过验证用户的细节点生成验证哈希表，与注册哈希表对比，获取真实细节点在模糊保险箱中对应的多项式点集，用于重构多项式，释放密钥（如图4所示）。

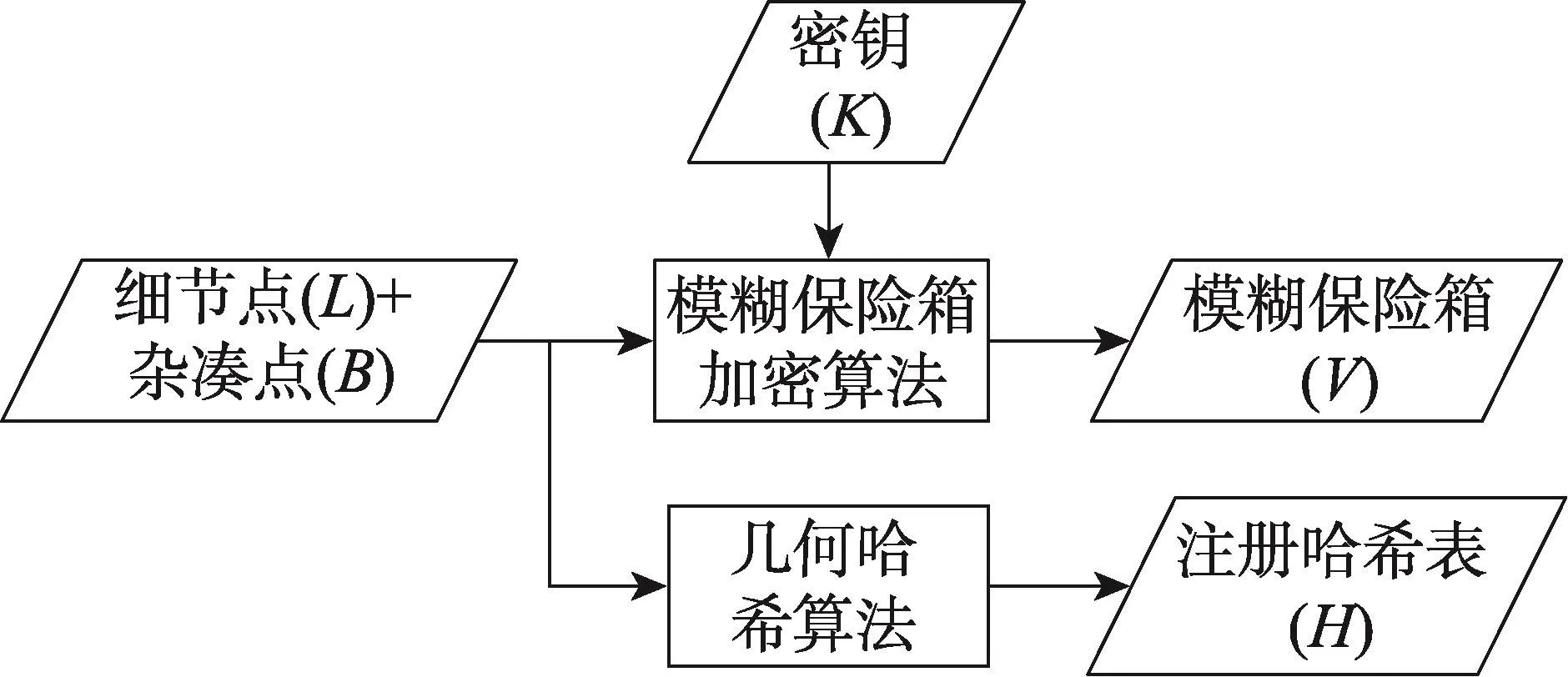
Fig.3 Template register of fuzzy vault for fingerprint based on geometric hashing algorithm图3 基于几何哈希法的指纹模糊保险箱模板注册

基于2.1节介绍的例子，几何哈希算法是利用指纹Fuzzy Vault算法中提取的细节点集L={mi=(xi,yi,θi,ti)|1 ≤ i≤ 4}和杂凑点集 B={ci=(xi′,yi′,θi′,ti′)|1 ≤ i≤2}进行校准，本文使用的细节点类型都是端点。该算法的具体实现过程如下。

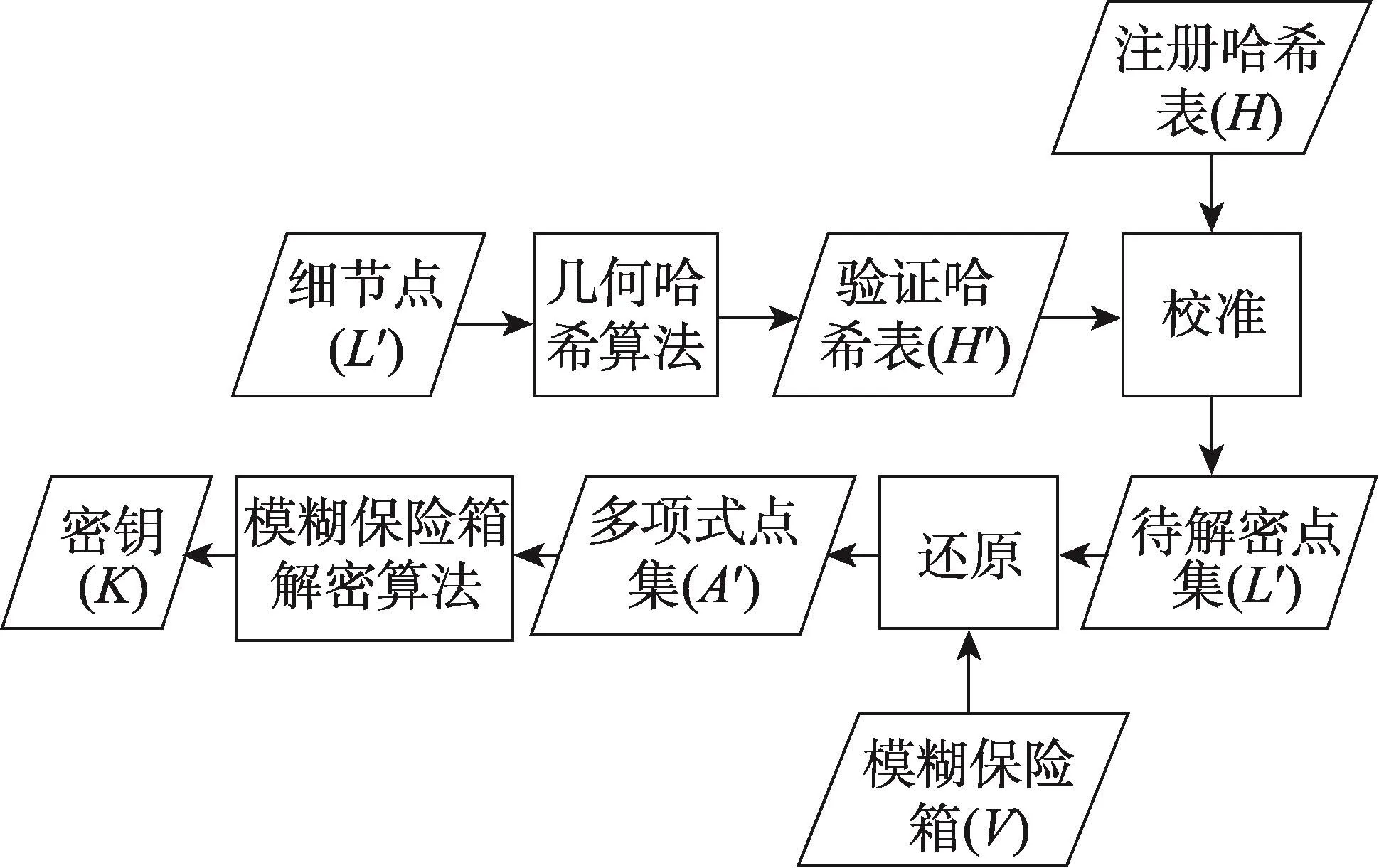
Fig.4 Template verification of fuzzy vault for fingerprint based on geometric hashing algorithm图4 基于几何哈希法的指纹模糊保险箱模板验证

（1）注册阶段

① 以 m1=(x1,y1,θ1,t1)为基点，即 m1(1)=(1,1,1,1)，将剩下所有的点m2、m3、m4、c1、c2分别代入到几何哈希变换公式（1）中进行旋转和平移变换，即TRmj(1)表示第 j个细节点进行旋转和平移后的结果，共变换5次，结果用集合T1={mj(1)=(xj(1),yj(1),θj(1),tj(1))|1＜j≤6}表示，并将得到的6个结果依照m1、m2、m3、m4、c1、c2的顺序排列作为注册哈希表的第1行元素。

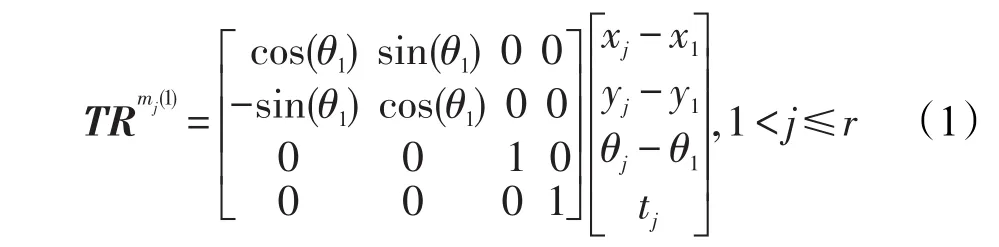
②分别以点 m2、m3、m4、c1、c2为基点，按照步骤①重复进行变换，最终得到注册哈希表的第2至第6行。

③为减少信息量，需要对哈希表进行量化，量化公式如式（2）所示，α表示坐标量化参数，β表示角度量化参数。式（2）仅代表对哈希表的第1行进行量化的结果，将剩余行依次进行量化后即完成了注册阶段工作，得到注册哈希表，如式（3）所示。

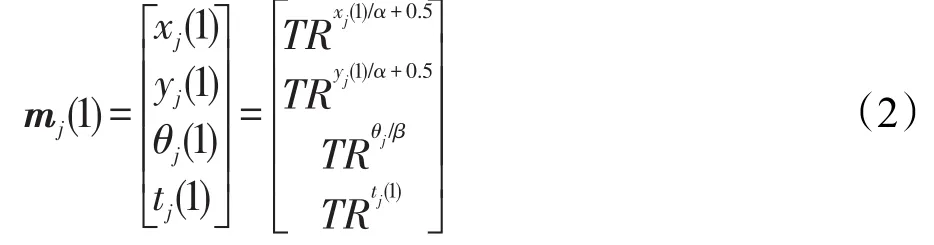
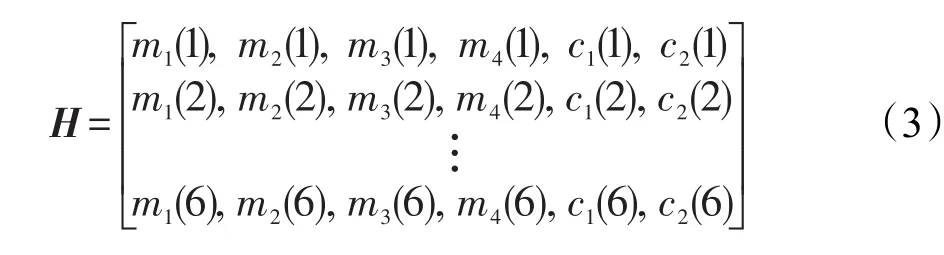
（2）验证阶段

①验证过程生成哈希表的原理与注册时相同，但细节信息仅包含真实细节点，不再添加杂凑点。提取验证用户的真实细节点集Q={mi′=(xi,yi,θi,ti)|1≤i≤4}，真实细节点的个数至少大于等于3才能重构多项式，本文提取了4个细节点，通过几何哈希变换形成一个验证哈希表，如式（4）所示。

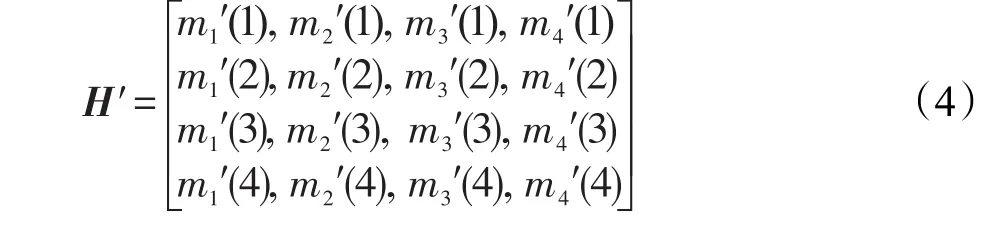
②将验证哈希表中的第1行与注册哈希表的每一行进行对比，每个点中的x、y、θ、t值都相近时该点值表示为1，视为相近的x、y坐标容忍度为d，角度容忍范围为l，理想情况下，结果如式（5）所示。

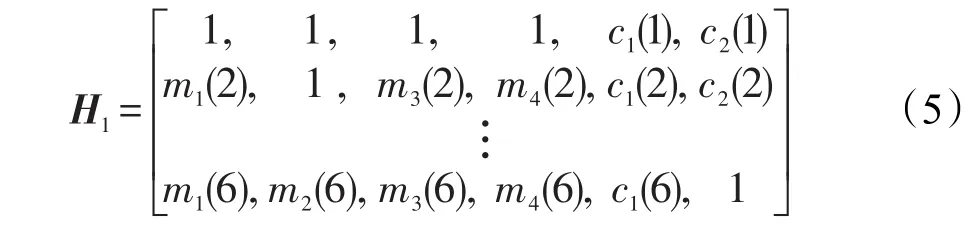
③统计注册哈希表中每一行值为1的个数，找出数量最多的一行，如果该行1的数量小于多项式系数的个数（本例中多项式系数的个数为3），即无法重构出本文的二阶多项式，则依据步骤②继续对比验证哈希表的下一行；如果个数大于等于3，则找出值为1对应位置所表示的所有细节点集L={mi=(xi,yi,θi,ti)|1≤i≤n}，根据排列组合原理，得到从中选择3个细节点的所有组合方式，即。

④将选择出的3个细节点作为待解密的真实细节点集L′={mi=(xi,yi)|1≤i≤3}，还原出模糊保险箱中对应的多项式点集A′={ti=(xi|yi,P(xi|yi))|1≤i≤3}，通过多项式重构，恢复出多项式系数a、b、c，再进行CRC校验，如果结果为0，则匹配成功，释放密钥K={a,b}，否则重复进行步骤④。

⑤如果所有组合都校验失败，则返回到步骤②，继续将验证哈希表中的第2行至6行的值与注册哈希表的每行进行对比，直到CRC校验为0，匹配成功，释放密钥K；如果注册哈希表的所有行中1的个数都小于3，或所有待解密细节点集L′的组合都校验失败，则视为非同一用户的指纹信息，无法恢复密钥K。至此，整个校准过程结束。

对于验证哈希表的每行与注册哈希表进行对比时，容忍度范围d、l的选取，文献[26]通过实验分析得到，x、y坐标容忍度选为[-3,3]，角度容忍范围是22.5°。

在描述重现算法的过程中，指纹图片细节点的提取个数，选取多少个细节点作为基点进行校准，以及哈希表量化参数（α和β）的取值都需要进一步确定。但是，在算法描述中这些参数都没有明确标注，导致实现更为复杂。并且在设置不同值进行实验时，得到的算法精度差别很大。因此，本文对以上参数取值进行了分析和优化。其中，指纹图片提取细节点的个数与设置的图片像素有关，即不同图片像素下能够提取出的细节点个数不同。

3 细节点提取与量化影响因素分析和改进

根据算法分析，匹配时图片像素大小、哈希表基点数以及哈希表量化参数（α和β）的范围都直接影响匹配结果的精度。因此，本文选择以上3个参数作为目标变量，分别以提取出的细节点个数、拒真率（false rejection rate，FRR）、认假率（false acceptance rate，FAR）作为目标函数。基于指纹库FVC2004，对不同参数取值下的匹配精度进行实验分析。

3.1 图片像素大小对算法的影响分析

图片像素的设置决定了算法能够提取出指纹细节点的数量。指纹库中的图片或实际采集的图片像素并不相同，因此算法在设定图片像素的大小时，需要满足能够提取出足够的细节点用于匹配。本文对指纹库FVC2004中的图片进行细节点提取，设置指纹图片像素在200×200到400×400之间，统计细节点个数如图5所示。从图中可以看出，图片像素太小严重影响了细节点的提取效果，像素越大，效果越好。当像素值达到300左右时，能够取出足够的指纹细节点用于指纹Fuzzy Vault算法中，约为70个；当像素值达到330左右时，可以取出指纹图片上所有的细节点，约为120个。

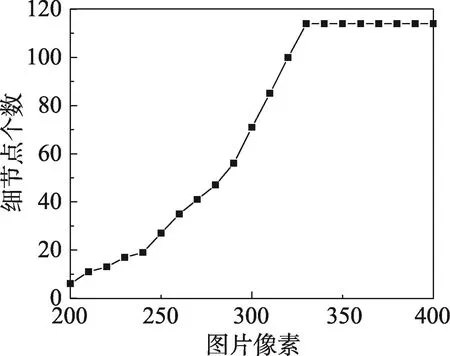
Fig.5 Influence of image pixel on the number of minutiae图5 图片像素对细节点个数的影响

另一方面，模糊保险箱算法在加密过程中将细节点的坐标值x、y级联为x|y后转换到有限域GF（216）中，即x、y的坐标范围应在[0,255]之间，才能保证细节点坐标值不超出域值，因此并不是图片像素值越大越好。针对此问题，根据指纹图片上细节点一般集中在中央位置，本文对细节点的选取加以约束。算法提取出细节点后，对细节点的横坐标和纵坐标进行筛选，去除掉坐标值超过范围[0,255]的边缘点，保留范围内的点，保证了所有用于模糊保险箱加密的细节点级联后都在有限域GF（216）内，避免了算法超出域值的错误。

因此，在算法中将图片像素设定为300×300，然后对细节点坐标进行筛选，并在指纹库FVC2000、FVC2002和FVC2004中验证，结果证明优化方案可行。

3.2 哈希表基点数对算法的影响分析

通过几何哈希变换生成一个几何哈希表，最基本的要素是基点，即本文2.2节中提到的细节点集L={mi=(xi,yi,θi,ti)|1≤i≤4}，例子中为便于说明，基点的个数设为4。实际在指纹Fuzzy Vault算法的匹配过程中，基点个数影响了算法的匹配精度，是非常关键的一个参数。基于此，本研究设计实验对基点个数的选取进行分析。指纹图片基于指纹库FVC2004，图片像素值设置为300×300。对于多项式阶数的设定，文献[21，23，27，29]等对不同阶数的多项式得到的算法匹配精度进行了说明：多项式阶数越多，算法的拒真率越高，认假率越低。但是，在本文实现算法时发现，多项式阶数越高，导致算法的运行时间越长，时间性能越差。因此，将多项式阶数设定为8。然后，选择多个同源和非同源的指纹模板进行实验测试，统计算法结果的拒真率和认假率，如图6所示。实验结果表明，选取基点的个数太少或太多，算法的匹配精度都不高，基点个数的最优取值范围应选择在20个左右。

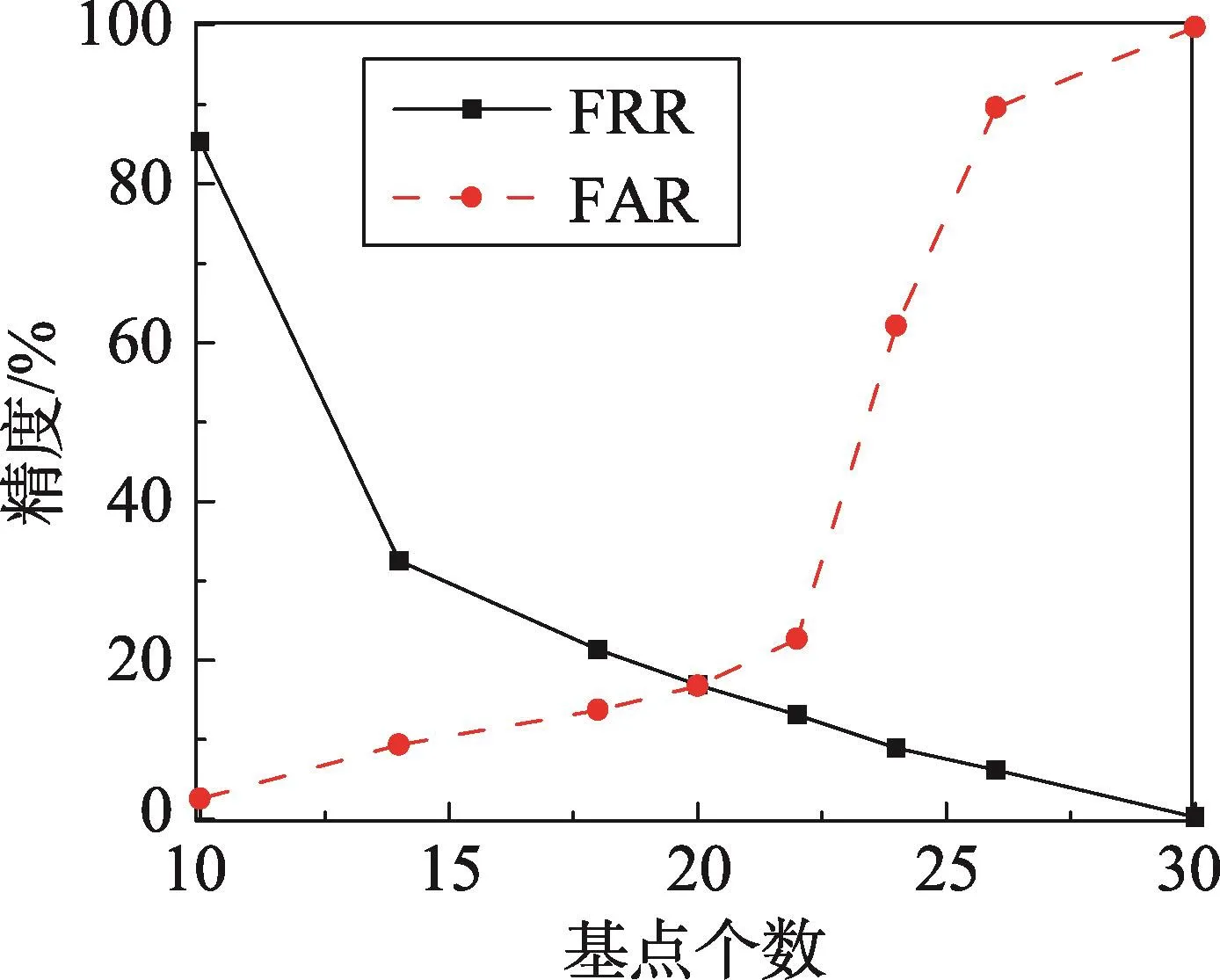
Fig.6 Influence of hash table basis points number on accuracy图6 哈希表基点个数对精度的影响

另一方面，通过几何哈希的变换公式（1）对细节点的坐标进行变换时发现，细节点之间的坐标距离越大，转换后得到数值差异越大，从而在验证过程中将注册和验证哈希表进行对比时，减少了因数值差异小而导致本不是对应的细节点被误识为同一细节点的出现次数。综上所述，本文对基点选取进行了优化，设置在提取出的细节点选取为基点时，能够作为一个基点的细节点选取标准是与其他基点的坐标值距离在10以上，即10，否则将不被视为一个基点。

因此，本文进行几何哈希自动校准时，选取了20个细节点作为基点，并对选取基点的坐标距离进行了优化。通过在指纹库FVC2000、FVC2002和FVC2004中验证，结果证明优化方案可行。

3.3 哈希表量化参数（α和β）对算法的影响分析

几何哈希自动校准算法中，基点是以指纹模板中细节点的实际值为基准，没有进行有限域GF（216）的转换，从而通过平移、旋转后形成的哈希表中数据量较大，一般达到小数点后4位以上，导致存储空间较大，影响算法性能，因此需要将哈希表进行量化以减少数据量。但是，量化参数取值不同，量化后哈希表数值也不同，对算法的匹配精度会造成一定影响。基于此，量化参数α和β的取值需要进一步确定，但现有文献并没有对其进行具体说明。本文对几何哈希算法量化公式（2）中的量化参数α和 β值进行实验分析（如图7、图8所示），指纹图片仍然基于指纹库FVC2004，设置图片大小为300×300像素，多项式阶数为8，用于对比的基点个数为20。从数据可以看出，随着α和 β值的增加，拒真率越来越低，认假率越来越高，即量化值越大，同一人的指纹匹配成功率和不同人的指纹匹配成功率都升高。为保证算法性能，α值应在[2,3]之间，β值应在[1.0,1.5]之间。

为得到更精确的参数数值，根据实验数据，在α的[2,3]范围内，β 的[1.0,1.5]范围内，对FRR、FAR的值求平均数 AVG（average），即AVG=(FRR+FAR)/2。结果得到α=2.6，β=1.0时，AVG的值最小，匹配精度最高。

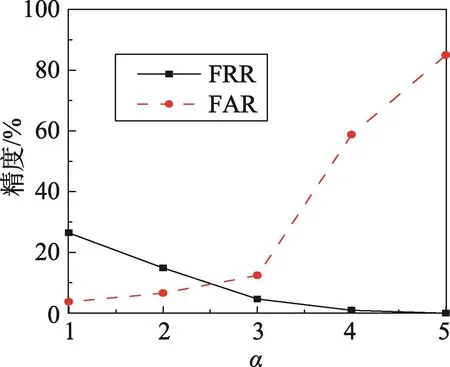
Fig.7 Influence of hash table quantization parameterαon accuracy图7 哈希表量化参数α对精度的影响

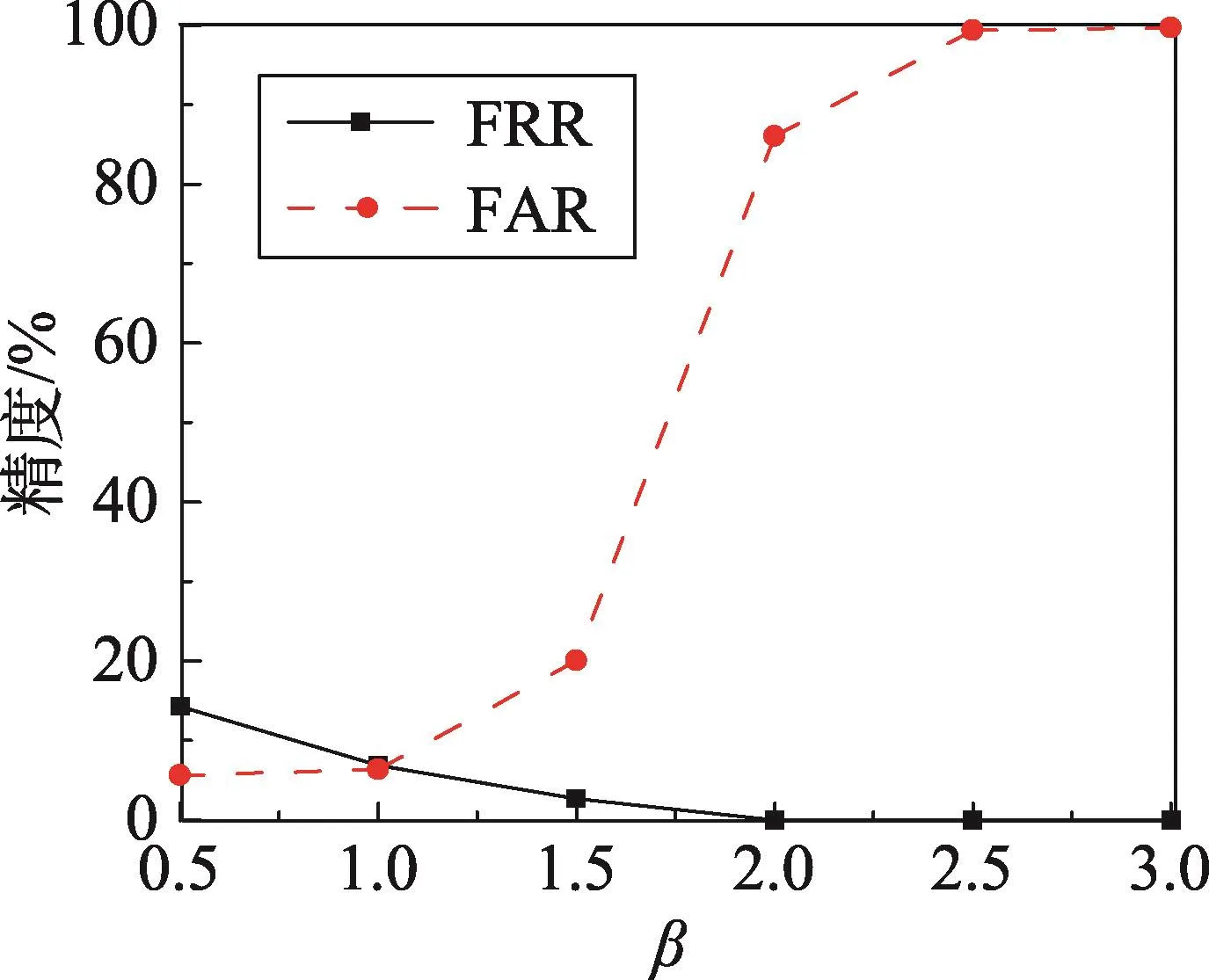
Fig.8 Influence of hash table quantization parameterβon accuracy图8 哈希表量化参数β对精度的影响

4 实验验证与结果分析

为了验证本文得出的指纹FuzzyVault算法优化方案的可行性，在软件Matlab 7.6.0（R2008a）上进行验证实验。基于指纹库FVC2000、FVC2002和FVC2004，每个指纹库中的同源指纹图片和非同源指纹图片分别进行实验300次，统计算法优化前和优化后的匹配精度。对于优化前算法参数的选取，图片像素值设为250×250，基点个数设为15，多项式阶数为8，α和β的值分别为2和1；对于优化后的算法，图片像素值为300×300，基点个数设为20，多项式阶数为8，α和β的值分别为2.6和1.0。实验的精度对比结果如表1所示。

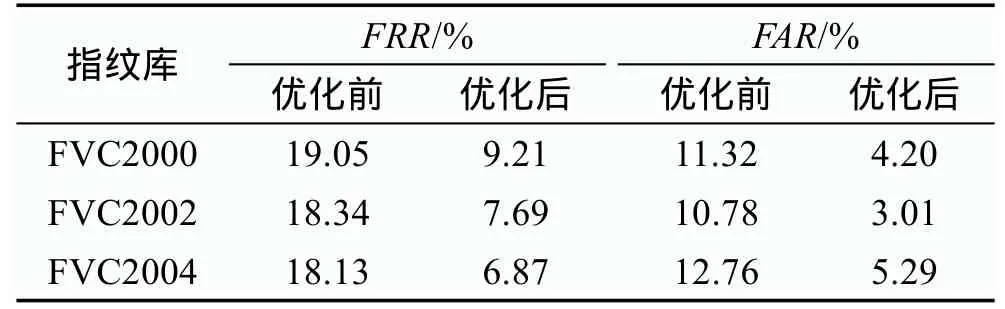
Table 1 Matching accuracy comparison of algorithm before and after optimization in differentfingerprint databases表1 算法优化前和优化后在不同指纹库中的匹配精度对比

从表1中可以看出，算法优化后在3个库中的匹配精度都有所提高，对于拒真率，FVC2000库降低的百分比最少，为9.84%，FVC2004库最多，为11.26%；对于认假率，FVC2000库降低最少，为7.12%，FVC2002库最多，为7.77%。说明本文的优化方案应用在不同的指纹库时，都提高了匹配精度，具有较好的普遍性，并且提高的幅度是较为稳定的，具有良好的鲁棒性，因此该优化方案可实际应用。另一方面，对于不同库的精度提高不同，在统计结果时发现FVC2002中的DB2、DB4与FVC2004中的DB4这些子数据库的精度提高效果明显，分析主要原因是与库中指纹图片识别难度有关，而造成识别难度不同的原因有采集仪、志愿者等。

对于优化算法的时间性能，文中统计了上述验证过程中算法的平均时间消耗，在7.148 028 s左右，而主要时间消耗在指纹图片的细节点提取过程，约为6.902 138 s，因此指纹模糊保险箱过程消耗时间仅为0.245 890 s。

5 结束语

本文基于生物特征加密技术领域中应用最为广泛的指纹模糊保险箱（fuzzy vault）算法，针对算法中的自动校准过程，采用几何哈希算法实现指纹图片的自动校准。对算法中几个关键参数，即图片像素大小、哈希表基点数和哈希表量化参数（α和 β）进行了实验分析，统计了参数的最优取值范围。然后，对几何哈希校准算法中的细节点提取和基点选取规则进行了优化。最后，通过多个不同指纹库进行实验，验证了算法优化方案的正确性，使几何哈希自动校准算法更加的实用化。

[1]Schmidt G J,Soutar C,Tomko G J.Fingerprint controlled public key cryptographic system:USA,5541994[P].1996.

[2]Juels A,Sudan M.A fuzzy vault schem[J].Designs,Codes and Cryptography,2006,38(2）:237-257.

[3]Clancy T C,Kiyavash N,Lin D J.Secure smartcard based fingerprint authentication[C]//Proceedings of the 2003 ACM SIGMM Workshop on Biometrics Methods and Applications,Berkley,USA,Nov 8,2003.New York:ACM,2003:45-52.

[4]Uludag U,Pankanti S,Jain A K.Fuzzy vault for fingerprints[C]//LNCS 3546:Proceedings of the 5th International Conference on Audio-and Video-Based Biometric Person Authentication,Hilton Rye Town,USA,Jul 20-22,2005.Berlin,Heidelberg:Springer,2005:310-319.

[5]Moon D,Choi W Y,Moon K,et al.Fuzzy fingerprint vault using multiple polynomials[J].World Academy of Science Engineering&Technology,2009,59:290-293.

[6]Nagar A,Nandakumar K,Jain A K.A hybrid biometric cryptosystem for securing fingerprint minutiae templates[J].Pattern Recognition Letters,2010,31(8):733-741.

[7]Tan Taizhe,Zhang Hongyan.An improved fingerprint vault fuzzy encryption scheme[J].Computer Application Research,2012,29(6):2208-2210.

[8]Benhammadi F,Bey K B.Password hardened fuzzy vault for fingerprint authentication system[J].Image&Vision Computing,2014,32(8):487-496.

[9]Malkauthekar M D.Template security for fingerprint recognition system with two variables polynomial of fuzzy vault for minutiae points[C]//Proceedings of the 2015 International Conference on Communications and Signal Processing,Melmaruvathur,India,Apr 2-4,2015.Piscataway,USA:IEEE,2015:1856-1859.

[10]Moon D,Chung Y,Seo C,et al.A practical implementation of fuzzy fingerprint vault for smart cards[J].Journal of Intelligent Manufacturing,2014,25(2):293-302.

[11]Lee Y J,Bae K,Lee S J,et al.Biometric key binding:fuzzy vault based on iris images[C]//LNCS 4642:Proceedings of the 2007 International Conference on Advances in Biometrics,Seoul,Aug 27-29,2007.Berlin,Heidelberg:Springer,2007:800-808.

[12]Sowkarthika S,Radha N.Securing iris and fingerprint templates using fuzzy vault and symmetric algorithm[C]//Proceedings of the 7th International Conference on Intelligent Systems and Control,Coimbatore,India,Jan 4-5,2013.Piscataway,USA:IEEE,2013:189-193.

[13]Wu Xiangqian,Wang Kuanquan,Zhang D.A cryptosystem based on palmprint feature[C]//Proceedings of the 19th International Conference on Pattern Recognition,Tampa,USA,Dec 8-11,2008.Washington:IEEE Computer Society,2008:1-4.

[14]Lu L,Teoh A B J.Alignment-free row-co-occurrence cancelable palmprint fuzzy vault[J].Pattern Recognition,2015,48(7):2290-2303.

[15]Wu Yongdong,Qiu Bo.Transforming a pattern identifier into biometric key generators[C]//Proceedings of the 2010 International Conference on Multimedia and Expo,Singapore,Jul 19-23,2010.Washington:IEEE Computer Society,2010:78-82.

[16]Eskander G S,Sabourin R,Granger E.A bio-cryptographic system based on offline signature images[J].Information Sciences,2014,259(3):170-191.

[17]Yang Shenglin,Verbauwhede I.Automatic secure fingerprintverification system based on fuzzy vault scheme[C]//Proceedings of the 2005 International Conference on Acoustics,Speech,and Signal Processing,Philadelphia,USA,Mar 18-23,2005.Piscataway,USA:IEEE,2005:609-612.

[18]Nandakumar K,Jain A K,Pankanti S.Fingerprint-based fuzzy vault:implementation and performance[J].Information Forensics and Security,2008,2(4):744-757.

[19]Tico M,Kuosmanen P.Fingerprint matching using an orientation based minutia descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(8):1009-1014.

[20]Jiang Xudong,Yau W Y.Fingerprint minutiae matching based on the local and global structures[C]//Proceedings of the 15th International Conference on Pattern Recognition,Barcelona,Spain,Sep 3-8,2000.Washington:IEEE Computer Society,2000:6038-6041.

[21]Li Peng,Yang Xin,Cao Kai,et al.An alignment-free fingerprint cryptosystem based on fuzzy vault scheme[J].Journal of Network and ComputerApplications,2010,33(3):207-220.

[22]Nasiri AA,Fathy M.Alignment-free fingerprint cryptosystem based on multiple fuzzy vaults[C]//Proceedings of the 2015 International Symposium on Artificial Intelligence and Signal Processing,Mashhad,Iran,Mar 3-5,2015.Piscataway,USA:IEEE,2015:455-458.

[23]Tams B.Absolute fingerprint pre-alignment in minutiaebased cryptosystems[C]//Proceedings of the 12th International Conference of Biometrics Special Interest Group,Darmstadt,Germany,Sep 4-6,2013.Piscataway,USA:IEEE,2013:75-86.

[24]Yang Wencheng,Hu Jiankun,Wang Song.A Delaunay quadrangle-based fingerprint authentication system with template protection using topology code for local registration and security enhancement[J].IEEE Transactions on Information Forensics&Security,2014,9(7):1179-1192.

[25]Chen Hantao,Hu Xuxiao.Research on fingerprint image matching algorithm based on the spectrum of detail points[J].Journal of Zhejiang Sci-Tech University,2015,33(6):858-863.

[26]Chung Y,Moon D,Lee S,et al.Automatic alignment of fingerprint features for fuzzy fingerprint vault[C]//LNCS 3822:Proceedings of the 1st SKLOIS Conference on Information Security and Cryptology,Beijing,Dec 15-17,2005.Berlin,Heidelberg:Springer,2005:358-369.

[27]Moon D,Lee S,Chung Y,et al.Implementation of automatic fuzzy fingerprint vault[C]//Proceedings of the 7th International Conference on Machine Learning and Cybernetics,Kunming,China,Jul 12-15,2008.Piscataway,USA:IEEE,2008:3781-3786.

[28]Han Caiyun,Liu Jiayong.Revocable automatic registration of fingerprint encryption scheme based on chaos mapping[J].Information Security and Communications Privacy,2014(4):110-113.

[29]Yao Xu,Liu Jiayong,Han Caiyun,et al.Multiple control fuzzy vault scheme based on fingerprint automatic registration[J].Journal of Sichuan University:Natural Sciences,2014,51(6):1205-1210.

[30]Tian Jie,Yang Xin.Biometric identification theory and application[M].Beijing:Tsinghua University Press,2009:390-393.

[31]Wolfson H,Riggoutsos I.Geometric hashing:an overview[J].IEEE Computational Science&Engineering,1997,4(4):10-21．

附中文参考文献:

[7]谭台哲,章红燕.一种改进的指纹Fuzzy Vault加密方案[J].计算机应用研究,2012,29(6):2208-2210.

[25]陈汉涛,胡旭晓.基于细节点频谱的指纹图像匹配算法研究[J].浙江理工大学学报,2015,33(6):858-863.

[28]韩彩芸,刘嘉勇.基于混沌映射的可撤销自动配准指纹加密方案[J].信息安全与通信保密,2014(4):110-113.

[29]姚旭,刘嘉勇,韩彩芸,等.基于指纹自动配准的多重控制模糊金库方案[J].四川大学学报:自然科学版,2014,51(6):1205-1210.

[30]田捷,杨鑫.生物特征识别理论与应用[M].北京:清华大学出版社,2009:390-393.

ZHANG Lu was born in 1991.She is an M.S.candidate at Tianjin Polytechnic University.Her research interests include biometric recognition and encryption.

张璐（1991—），女，山东德州人，天津工业大学硕士研究生,主要研究领域为生物特征识别与加密。

王金海（1966—），男，江西南昌人，2007年于天津大学物理电子学专业获得博士学位，现为天津工业大学教授、硕士生导师，主要研究领域为信号与信息检测与处理，嵌入式系统设计，生物医学电子检测技术。

CUI Jun was born in 1979.He received the Ph.D.degree in cryptography from Beijing University of Posts and Telecommunications in 2013.Now he is a lecturer at Tianjin Polytechnic University.His research interests include biometric recognition and encryption,identity authentication and access control.

崔军（1979—），男，湖南安乡人，2013年于北京邮电大学密码学专业获得博士学位，现为天津工业大学讲师，主要研究领域为生物特征识别与加密，身份鉴别，访问控制。

ZHAO Junfa was born in 1979.He received the Ph.D.degree from Nankai University in 2010.Now he is a lecturer at Tianjin Polytechnic University.His research interests include optical fiber sensor and biometric recognition.

赵军发（1979—），男，天津人，2010年于南开大学获得博士学位，现为天津工业大学讲师，主要研究领域为光纤传感，生物特征识别。

CHEN Hongyu was born in 1993.He is an M.S.candidate at Tianjin Polytechnic University.His research interests include biometric recognition and encryption.

陈泓宇（1993—），男，天津人，天津工业大学硕士研究生，主要研究领域为生物特征识别与加密。

Research on Parameters Optimization for Fuzzy Vault Algorithm of Template Alignment*

ZHANG Lu,WANG Jinhai,CUI Jun+,ZHAO Junfa,CHEN Hongyu
School of Electronics and Information Engineering,Tianjin Polytechnic University,Tianjin 300387,China

In the concrete implementation of fuzzy vault algorithm,geometric Hashing is a kind of common technology for the biometric template automatic alignment.To solve the fuzzy problem of parameters selection in the algorithm implementation,this paper studies three parameters which affect the matching accuracy:image pixels size,the number of basic points and quantitative parameters of a Hash table(α and β).The optimal ranges of three parameters are obtained by carrying out the factor experiment analysis.Then,the extracting range of the minutiae algorithm and the rule of selecting the distance of basis points can be further optimized.Finally,the matching accuracy before and after optimization is compared and validated by the fingerprint picture based on the FVC databases.The experimental results show that the proposed optimization scheme can improve the matching accuracy of the algorithm because the FRR(false rejection rate)is reduced by 9.84%,at least FAR(false acceptance rate)is reduced by 7.12%,and has a certain robustness and practicality.

fuzzy vault;biometric;geometric hashing algorithm;automatic alignment;fingerprint

the Ph.D.degree in physical electronics from Tianjin University in 2007.Now he is a professor and M.S.supervisor at Tianjin Polytechnic University.His research interests include signal and information detection and processing,embedded system design and biomedical electronics testing technology.

2016-06, Accepted 2016-12.

A

TP309.2

+Corresponding author:E-mail:cuijun@tjpu.edu.cn

ZHANG Lu,WANG Jinhai,CUI Jun,et al.Research on parameters optimization for fuzzy vault algorithm of template alignment.Journal of Frontiers of Computer Science and Technology,2017,11(9)：1451-1460.

10.3778/j.issn.1673-9418.1606064

*The Science and Technology Development Foundation of High Education of Tianjin under Grant No.20140805(天津市高等学校科技发展基金计划项目).

CNKI网络优先出版: 2016-12-21, http://www.cnki.net/kcms/detail/11.5602.TP.20161221.1128.010.html