考虑线型因子的变压器油纸绝缘系统微水含量评估

郑文迪， 蔡金锭， 曾静岚

(福州大学 电气工程与自动化学院，福建 福州 350116)

考虑线型因子的变压器油纸绝缘系统微水含量评估

郑文迪， 蔡金锭， 曾静岚

(福州大学 电气工程与自动化学院，福建 福州 350116)

针对现有的时域介质响应方法无法直观诊断变压器受潮情况，现从微观动力学的角度分析线型因子与微水含量的内在联系。提出的时域微分解析法将隐含在去极化电流曲线中的不同介质极化过程逐一分解，不但可求得线型因子，而且能直观地判断弛豫项数。通过对变压器测试曲线的解析结果表明，变压器的受潮程度与弛豫项数相关及线型因子有密切联系：弛豫项数越多，绝缘系统内部微水含量越多；绝缘系统受潮越严重，表征绝缘纸极化的线型因子越大。

油纸绝缘；变压器；微水含量；弛豫项数；线型因子

0 引 言

大型油浸式变压器的绝缘状态是影响电力系统安全运行的重要因素之一[1-2]，而微水的存在严重影响绝缘系统的电气寿命和机械寿命，其会降低绝缘系统的击穿电压并增加介质损耗，同时微水还直接参与纤维素等大分子的降解，加速整体的绝缘劣化过程，严重时可能导致设备击穿或烧毁[3-4]。因此采用有效方法及时地检测绝缘的微水含量，对于避免因绝缘问题引起停电事故具有重要意义[5-6]。

国内外有很多诊断油纸绝缘变压器微水含量的方法，例如油纸水平衡关系曲线法、露点法、卡尔费休滴定法等，但这些方法具有分析数据不易获取或可能对设备造成污染等缺点。而时域介质响应法是一种研究油纸绝缘系统受潮状态的无损诊断方法，具有抗干扰性强、携带信息丰富等特点[7-8]，能有效揭示绝缘介质在缓慢极化过程中的特性变化，克服了传统诊断方法数据不易获取、损害变压器的缺陷，因此被广泛应用于评估电力变压器油纸绝缘系统的微水含量。

近年来大部分学者通过建立介质响应的数学模型，从中挖掘时域特征量与油纸绝缘系统微水含量的内在联系。但是现有的建模方法仍然存在一些问题：1)现有的介质响应函数未能反映油纸绝缘介质的实际极化过程。如文献[9]和文献[10]中的介质响应数学模型是建立在假设偶极子松弛介质间不会相互作用的前提下，虽简化了计算但不够全面。2)现有的建模方法无法直观反映等效电路模型中弛豫项数和极化类型。如文献[11]和文献[12]通过人为假设固定的弛豫项数进行参数辨识，故这类寻优方法只是在数学上满足最优的结果，未能体现扩展德拜模型的物理意义。3)目前为止未见到应用去极化电流弛豫特征量直观、准确地评估绝缘系统的微水含量的相关文献和报道。如文献[13]和文献[14]是只是定性地分析在不同情况下去极化电流曲线的变化，而对去极化电流内部弛豫特性与微水含量的关系少有研究。

基于上述问题，本文引入微观动力学的线型因子以改进现有的数学模型，建立了带线型因子的介质响应函数[15]，该模型更符合介质的实际极化规律。同时根据时域微分谱函数的数学特性，提出了微分解析法用于弛豫过程的分解，不仅能直观地判断弛豫项数，还能反映不同类型的弛豫过程，体现极化的物理意义。最后通过分析弛豫项数、线型因子和绝缘系统微水含量的内在联系，提出评估变压器油纸绝缘系统受潮程度的新方法。

1 基于线型因子的介质响应函数建模

变压器油纸绝缘系统主要由绝缘油、绝缘纸、隔板、撑条和油隙构成。单一弛豫机构仅能描述某种介质的极化过程，对于复杂的油纸绝缘系统就不适应，因此大多数学者采用快慢相应速率不同的弛豫机构项叠加，来描述油纸绝缘材料的极化过程，即采用基于扩展Debye形式的介质响应函数模型[16]，其数学表达式为

(1)

式中：n为弛豫机构的数目；Bi为第i个弛豫机构作用所占的比重；ti表示第i个弛豫机构极化的时间常数。基于扩展Debye形式的变压器油纸绝缘等值电路如图1所示[17]。

图1 扩展Debye模型的等效电路Fig.1 Dielectric response equivalent circuit based on extended Debye model

图1中，Rg和Cg分别是绝缘电阻和工频下的几何电容，与绝缘结构有关；Ri和Ci(i=1,2,…，n)分别代表极化电阻和极化电容，二者串联的极化支路用于描述不同弛豫时间ti=RiCi的极化过程；n为等效的极化支路数，也就是弛豫项数，然而扩展Debye的介质响应函数是在假设偶极子松弛介质间不会相互作用的前提下获取的。李景德、曹万强等学者通过大量的压电实验和电极化实验发现，介质极化过程并不是单一指数衰减形式的叠加，同一种介质在不同的外界条件下的极化过程将呈现两种不同的弛豫规律[15]。热释电弛豫数据表明，在外加电场的作用下，介质极化呈现出单指数的衰减形式，其极化称为随机弛豫；而在无外电场、应力且恒温的情况下，介质的极化过程呈现出开方根指数衰减的特点[18]。随机弛豫和自由弛豫可分别表示成以下2种极化阶跃响应函数的形式[15]：

FR(t)=e-t/τi，

(1)

(2)

其中：下标R表示随机弛豫，F表示自由弛豫。

综合以上2种极化现象，随机弛豫和自由弛豫的指数衰减形式的幂具有1和1/2两个典型值，再进一步结合实际极化中扩散作用可能部分地制约弛豫过程，则衰减指数的幂被约束在1/2至1之间[19]。因此，可引入微观动力学标志——线型因子αi，整个弛豫过程呈现方根指数衰减规律，改进后的非典型线型介质响应函数表达式如式(3)所示。

(3)

式(3)的介质响应函数可看作由n个弛豫机构的不同方根指数衰减项之和。不仅考虑了2种弛豫现象，且综合了实际扩散作用的影响，使之更贴近实际的极化规律。

当各弛豫项的线型因子αi=1时，可得到扩展Debye形式的介质响应模型，这种传统的模型仅考虑了随机弛豫过程。若按经典德拜模型定义弛豫时间，则在自由弛豫过程中，将导致方根指数型衰减规律exp(-(t/t)1/2)通过若干指数衰减函数exp(-t/t)叠加进行描述，弛豫时间t将失去其物理意义[15]。

对于复合绝缘介质，绝缘油显弱极性，而绝缘纸属于极性介质，二者建立极化、去极化过程的时间不同，两者将在介质响应函数上呈现出较大线性因子αi的差异。变压器在长期高温下运行时，内部的金属粉屑和水等杂质会加速绝缘系统的氧化过程，绝缘油中某些高分子烃类和绝缘纸中纤维素大分子的化学键均会发生断裂，产生糠醛、酮、酸、CO、CO2和微水等老化产物。尤其是微水这类强极性物质的存在，会进一步加剧绝缘油的劣化，加速绝缘纸板的水降解和氧化降解过程，使得绝缘油和绝缘纸的极化速率大大提高。不同的微水含量对介质极化过程的加速程度不一，线型因子αi上的大小也不尽相同。因此通过分析表征油纸绝缘系统极化速率的线型因子αi，即可准确地诊断出介质的微水含量。

2 时域微分谱函数的解析

实际中介质响应函数的数量级极小，无法通过直接测量获得准确的数值。由于去极化电流id和介质响应函数f(t)之间具有简单线性关系[5,9]，因此时域诊断中通常采用去极化电流id来解析介质响应函数，二者间的关系如下

id(t)=C0U0(f(t)-f(t+tc)+εrδ(t))。

(4)

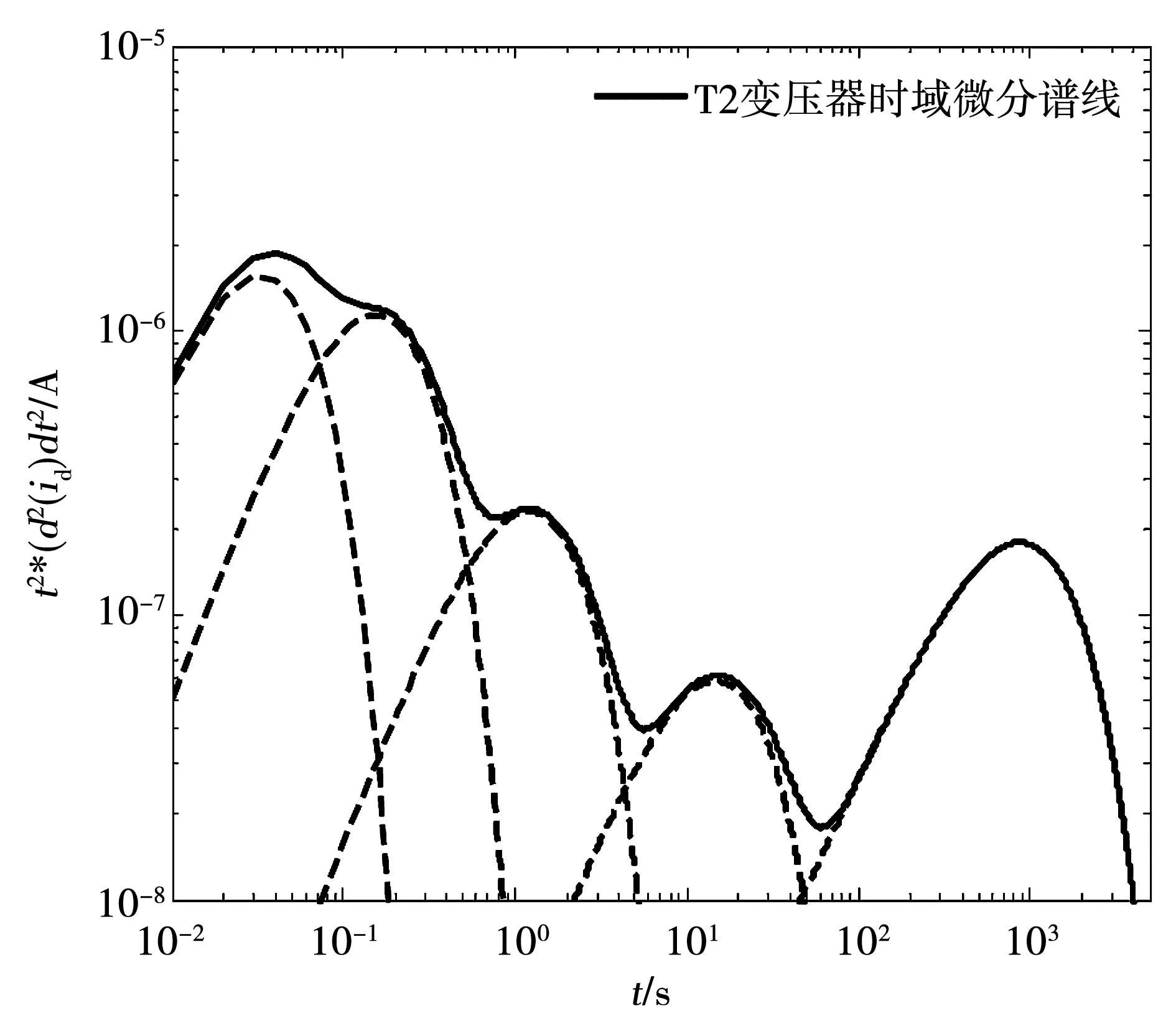
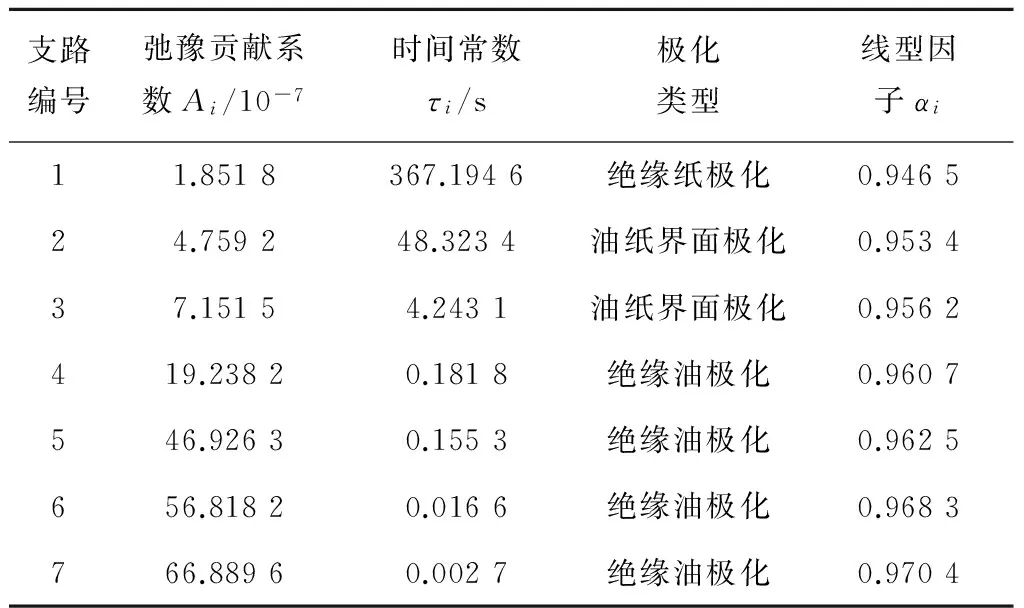
其中：C0代表绝缘系统的真空几何电容值；U0为直流的充电电压；tc为极化时间；εr表示相对介电常数。由于f(t)是方根指数衰减的形式，在极化时间tc足够长的情况下，满足f(t+tc)<

(5)

式中定义Ai=U0C0Bi为第i个机构的弛豫贡献系数。

由式(5)可见，去极化电流id也是由若干个方根指数衰减项的叠加而成，无法直接从去极化电流曲线直观地判断其弛豫项数，因此为了便于观察，现将去极化电流曲线转化为各单峰值曲线叠加作用的结果，对式(5)的谱函数进行二次微分处理，即

(t/τi)αiexp(-(t/τi)αi)=

(6)

其中：定义F(t)为时域微分谱函数，φi(t/τi,αi)为时域子谱线。

2.1 时域微分谱函数的特性分析

在αi>0，τi>0的前提下，时域子谱线φi(t/τi,αi)是一条单一峰值的凸函数，具体如图2所示。

图2 时域子谱线Fig.2 Time domain sub-line

下面对时域子谱线φi(t/τi,αi)的数学特性进行分析，为后续的微分解谱提供理论依据。从图2时域子谱线的曲线可以看出：

1)当00，则时域子谱线φi(t/τi,αi)是单调递增；

2)当timax

3)当t=timax时，dφi(t/τi,αi)/dt=0，则时域子谱线φi(t/τi,αi)具有唯一的峰值点。

其中，峰值时间的表达式如下：

(7)

根据上述分析，时域子谱线fi(t/τi,ai)具有以下特性：

特性1：时域子谱线φi(t/τi,αi)是一个单一峰值的凸函数，在t=timax时，φi(t/τi,αi)达到峰值，并随时间变化在峰值点的两侧逐渐衰减最后趋近于0；

特性2：线型因子αi决定子谱线的波形，定义φi=0.5φimax时对应的时宽为半高线，则时域子谱线φi(t/τi,αi)的半高线狭窄，若αi=1时，半高线仅为0.737；

特性3：以logφi为纵坐标时，在t<

特性4：由于τi和αi值的大小各异，则各时域子谱线φi(t/τi,αi)峰值点及其峰值时间也各不相同。故时域微分谱线F(t)是由n条单一峰值且峰值位置不同的时域子谱线叠加之和，F(t)中势必存在n个大小和位置不同的峰值点。

特性5：时间常数大的子谱线衰减缓慢，反之衰减的越快，故时间常数大的子谱线对二次时域微分谱线的末端贡献越大，反之贡献就越小，故对F(t)谱线末端影响可忽略不计。

2.2 时域微分谱函数的参数求解

时域微分谱线F(t)实质上是由若干个峰值点位置各不相同的子谱线叠加而成。图3给出了三条时域子谱线叠后的图形示意。通过上一节的分析可知，时域子谱线φi(t/τi,αi)的半高线较窄，不同弛豫时间的子谱线叠加后将出现n个局部峰值。因此可推断出图3时域微分谱线中的弛豫项数为3，即可直接从时域微分谱线的局部峰值数目判断弛豫项数。

图3 时域子谱线叠加Fig.3 Superimposed curve of time domain sub-line

综合以上分析，时域微分谱线F(t)的参数(Ai,τi,αi)求解过程如下：

步骤1：首先对去极化电流函数进行微分处理得到时域微分谱线，并对时域微分谱函数F(t)两端同取对数，根据谱线的局部峰值个数来确定弛豫项数n。

步骤2：从谱线末端开始，读取末端局部峰值的初始斜率即可解出αi，由局部峰值点(timax,Fimax)代入下式：

(8)

由式(8)求出Ai和τi，然后代入Aiφi(t/τi,αi)，即可求出第1条子谱线L1。将时域微分谱线减去第1条子谱曲线，得到剩余谱线Gi(*)。

步骤3：判断当前求解的子谱线数是否大于n。若i≥n，参数解析结束；若i

3 油纸绝缘系统微水含量评估

为了研究油纸绝缘系统弛豫项数和线型因子αi与微水含量的内在联系，分析了多台变压器测试的时域微分谱线。由于篇幅限制，现以表1所示的4台不同受潮程度的变压器为例，对其诊断过程进行具体阐述。表1中的微水含量是通过CA-100微水测定仪对变压器绝缘油样例进行测试获得的。

表1 各变压器的基本信息Table 1 Basic information of each transformer

去极化电流测试过程中，外加充电电压设置为1 000 V，充电/放电时间都为5 000 s，测试温度约为26 ℃，得到去极化电流曲线见图4。

3.1 弛豫项数与微水含量的联系

采用上述的微分解析法对图4的4条去极化电流曲线进行分解，可得到各变压器的时域微分谱线和各子谱线如图5～图8所示。

以油中微水含量作为变压器绝缘受潮程度的判断标准，T1变压器是新投入运行不久的变压器，微水含量较小，整体绝缘状态良好。从图5可以看出，T1变压器的时域微分谱线具有5个局部峰值，可推断出其介质响应中的弛豫项数为5。

图4 测试的去极化电流曲线Fig.4 Test depolarization current curve

图5 T1变压器时域微分谱线和各子谱线Fig.5 Time-differential line and each sub-lines of T1 transformer

对于运行多年的T2、T3变压器，整体绝缘水平一般，这两台变压器的时域微分谱线和各子谱线如图6和图7所示。从图6可见T2变压器的时域微分谱线具有5个局部峰值，其绝缘的弛豫项数为5。而从图7的时域微分谱线可以看出，T3变压器油纸绝缘内部具有6个局部峰值，其弛豫项数为6。

图6 T2变压器时域微分谱线和各子谱线Fig.6 Time-differential line and each sub-lines of T2 transformer

图7 T3变压器时域微分谱线和各子谱线Fig.7 Time-differential line and each sub-lines of T3 transformer

T4是受潮严重而退役的变压器，内部微水含量高达1.463%，其时域微分谱线的解谱情况如图8所示。可以看出T4变压器油纸绝缘系统具有7条极化支路，弛豫项数为7。

通过对比上述四台变压器的弛豫项数可大致得到以下结论：弛豫项数越多，油纸绝缘系统受潮越严重，内部微水含量就越多。这是因为，在去极化电流谱线中，它不仅包含了油纸绝缘系统内部的各介质的弛豫过程信息，而且也包含了与绝缘受潮有关的各种产物，如微水、醛、醇、酸和酮等的弛豫响应过程。微水的存在对绝缘物质的极化特性有着很大的影响，在外电场的作用下，绝缘介质中的极化将由束缚水和自由水的弛豫共同作用而引起的。同时，水分和纤维素的结合也将引起介质的界面极化，并降低绝缘介质的电导，增大其介质损耗。绝缘受潮的情况越严重，内部微水含量越高，从而引起越多的产物，则去极化电流谱线中包含的弛豫信息就越多，弛豫项数也就越多。反之，绝缘状况良好，微水含量越少，去极化电流曲线中包含的弛豫信息越少，弛豫项数就越少。

图8 T4变压器时域微分谱线和各子谱线Fig.8 Time-differential line and each sub-lines of T4 transformer

但是对于弛豫项数同为5的T1和T2变压器，T2变压器的微水含量远多于T1变压器，无法直接通过弛豫项数这一特征量诊断这两台变压器的绝缘受潮状态，因此需要进一步分析其他特征量与微水含量的内在联系。

3.2 线型因子与微水含量的联系

利用2.2节所述的解析法对表1变压器的时域微分谱函数进行参数辨识，可依次获得各个弛豫机构的线型因子。根据时间常数可将线型因子分为三类：1)小时间常数支路的线型因子(ti<1 s)反映绝缘油的极化过程；2)中时间常数支路的线型因子(1100 s)反映绝缘纸的极化状态[20]。现以表1变压器的解析结果为例，按时间常数值可将线型因子分为3类，不同微水情况下变压器解谱出的线型因子结果如表2～表5所示。

表2 T1变压器时域微谱线参数

表3 T2变压器时域微谱线参数

表4 T3变压器时域微谱线参数

表5 T4变压器时域微谱线参数

由表2～表5可以看出，随着微水含量从0.341%变化到1.463%，表征绝缘油极化(小时间常数支路)的最大线型因子从原来的0.949 9增至0.970 4；表征油纸界面极化(中时间常数支路)的最大线型因子从0.943 8增至0.956 2；而表征绝缘纸极化(大时间常数支路)的最大线型因子从0.827 3增加到0.946 5。可见表征绝缘纸极化的线型因子变化更明显，其对微水含量的变化反应更为灵敏，因此将绝缘纸的线型因子作为评估绝缘受潮状况的标准。

通过上述变压器分析诊断表明：随着受潮程度加剧，微水含量增加，绝缘纸的极化支路增加，绝缘纸极化的线型因子逐渐增大。这是因为水分属于强极性物质加快了绝缘介质中纤维素大分子的降解，产生酸类、芳香化合物和水分等老化产物，这类产物又进一步加剧绝缘系统整体的极化速率，从而线型因子增大。因此通过比较绝缘纸的线型因子可间接反映油纸绝缘系统的受潮状况。

对于新投入运行不久的T1变压器，其线型因子仅为0.827 3。而对于一般受潮状况的T2和T3变压器，表征绝缘纸极化的弛豫机构数为1，其线型因子处于0.89～0.90之间。虽然T1和T2的弛豫项数都为5，但T2的线型因子远大于T1，可推断出T2变压器的微水含量比T1多。T4为退役的变压器，其弛豫机构数明显增多，其线型因子更加接近于1，可推断出T4变压器油纸绝缘受潮严重，无法正常运行。实际中这台变压器确实存在绕组劣化、内部微水含量过高的问题，由此可见诊断结果和实际情况相符。

4 结 论

本文引入微观动力学的线型因子，改进了介质响应函数。在此基础上提出时域微分解析法用于去极化电流曲线弛豫过程的分解，不仅能根据谱线中的局部峰值点直接判断弛豫项数，还可以解析出弛豫机构的线型因子。通过对变压器的去极化电流曲线的解谱分析，可得到以下结论：

1)弛豫项数大体上可以反映油纸绝缘的受潮状况，弛豫项数越多，绝缘介质内部微水含量越多。

2)表征绝缘纸极化的线型因子对微水含量的变化反应灵敏，可作为评估油纸绝缘系统受潮状况的特征量。

3)绝缘纸的线型因子越大，内部微水含量越多，其受潮状态越严重，这为评估油纸绝缘受潮状态提供了新的思路和方法。

[1] 林智勇,蔡金锭. 运用混联等效电路诊断变压器油纸绝缘状态[J].电机与控制学报,2016,20(03):1. LIN Zhiyong, CAI Jinding. Diagnosing transformer oil-paper insulation by hybrid equivalent circuit[J].Electric Machines and Control，2016,20(03):1.

[2] 蔡金锭,曾静岚,李安娜. 采用I-APSO算法的弛豫响应等效电路参数辨识[J].电机与控制学报,2015,19(11):78. CAI Jinding,ZENG Jinglan, LI Anna.Parameter identification for equivalent circuit of relaxation response based on interval-active particle swarm optimization algorithm[J].Electric Machines and Control，2015,19(11):78.

[3] 柯春俊,林春耀,欧小波,等.步进电压下变压器匝间绝缘电压寿命指数新解法[J].哈尔滨理工大学学报,2016,21(05): 66. KE Chunjun,LIN Chunyao,OU Xiaobo,et al.New solving method for voltage endurance coefficient N of transformer turn-to-turn insulation under step-voltage[J].Journal of Harbin University of Science and Technology,2016,21(05): 66.

[4] 张明泽,赵东旭,黄玲,等.变压器油纸绝缘含水量的介电响应测量方法[J].哈尔滨理工大学学报,2016,21(02): 84. ZHANG Mingze,ZHAO Dongxu,HUANG Ling,et al.Dielectric response measuring method on moisture content of oil-paper insulation in transformer[J].Journal of Harbin University of Science and Technology,2016,21(02): 84.

[5] 张秋也,朱学成,高自伟,等.温度对油、纸介电参数及复合电场分布的影响[J].哈尔滨理工大学学报,2015,20(06): 59. ZHANG Qiuye,ZHU Xuecheng,GAO Ziwei,et al.Influence of temperature on dielectric parameters of oil & pressboard and the electric field distribution of oil-paper insulation under compound voltage[J].Journal of Harbin University of Science and Technology,2015,20(06):59.

[6] 杨丽君,齐超亮,邓帮飞,等.采用修正Cole-Cole模型提取油纸绝缘频域介电谱的特征量方法[J].高电压技术,2013,39(2): 310. YANG Lijun,QI Chaoliang,DENG Bangfei,et al.Application of modified Cole-Cole model to extract characteristics of frequency dielectric spectroscopy of oil-paper insulation [J].High Voltage Engineering,2013,39(2): 310.

[7] 廖瑞金,孙会刚,袁泉,等．采用回复电压法分析油纸绝缘老化特征量[J].高电压技术，2011,37(1):136. LIAO Ruijin,SUN Huigan,YUAN Quan,et a1.Analysis of oil-paper insulation aging characteristics using recovery voltage method [J].High Voltage Engineering,2011,37(1): 136.

[8] 唐勇波,桂卫华,彭涛,等.基于互信息变量选择的变压器油中溶解气体浓度预测[J].仪器仪表学报,2013,34(7): 1492. TANG Yongbo,GUI Weihua,PENG Tao,et al.Prediction method for dissolved gas concentration in transformer oil based on variable selection of mutual information[J].Chinese Journal of Scientific Instrument,2013,34(7): 1492.

[9] SAHA T K,PURKAIT P.Investigation of polarization and depolarization current measurements for the assessment of oil-paper insulation of aged transformers[J].IEEE Transactions on Dielectrics and Electrical Insulation,2004,11(1): 144.

[10] SAHA T K,PURKAIT P,MULLER F.Deriving an equivalent circuit of transformers insulation for understanding the dielectric response measurements[J].IEEE Transactions on Power Delivery,2005,20(1): 149.

[11] 张涛,蔡金锭.油纸绝缘变压器介质响应电路参数辨识的研究[J].电工电能新技术,2010,29(4): 35. ZHANG Tao,CAI Jinding,Research on parameters identification for dielectric response equivalent circuit of transformers with oil-paper insulation[J].Advanced Technology of Electrical Engineering and Energy,2010,29(4): 35.

[12] 林智勇,蔡金锭.油纸绝缘极化等效电路参数计算方法[J] .电机与控制学报,2014,18(8):62. LIN Zhiyong,CAI Jinding.Novel method to calculate polarized equivalent circuit of oil-paper insulation[J].Electric Machines and Control,2014,18(8):62.

[13] 唐盼,尹毅,吴建东,等.基于去极化电流法的变压器油纸绝缘状态[J].电工电能新技术,2012,31(4):39. TANG Pang,YIN Yi,WU Jiandong,et al.Study of oil-paper insulated transformers’ aging state based on depolarization current measurements[J].Advanced Technology of Electrical Engineering and Energy，2012， 31(4):39．

[14] 李军浩,胡泉伟,吴磊,等.极化/去极化电流测试技术的仿真研究[J].陕西电力,2011,39(4): 1. LI Junhao,HU Quanwei,WU Lei,et al.Simulation Study of polarization and depolarization current measurements technology[J].Shanxi Electric Power,2011,39(4): 1.

[15] 李景德,曹万强,李向前,等.时域介电谱方法及其应用[J].物理学报,1996,45(7): 1225. LI Jingde,CAO Wangxiang,LI Xiangqiang,et al.Time domain dielectric spectroscopy method and its application[J].Acta Physica Sinica,1996,45(7): 1225.

[16] 张涛.基于回复电压特征量的变压器油纸绝缘状态诊断研究[D] .福州大学,2010: 60-63.

[17] JOTAAP R S,ISLAM S M,JOTA F G.Modeling the polarization spectrum in composite oil-paper insulation systems[J].IEEE Trans.on Dielectrics and Elec.Insulation,1999,6(2): 145.

[18] 李功新,江修波,蔡金锭,等.采用微分去极化电流法解析变压器油纸绝缘的介质响应函数[J].高电压技术,2012,38(8):1930. LI Gongxin,JIANG Xiubo,CAI Jinding,et al.Dielectric response function for transformer oil-paper insulation solved by method of differential depolarization current[J].High Voltage Engineering,2012,38(8):1930.

[19] 沈韩，时域介电谱的非典型线型[J].中山大学研究生学刊(自然科学版)，1997,18(4):4. SHEN Han.Non-typical line shape of time domain dielectric spectroscopy[J].Natural Science Journal of the Graduates.Sun Yat-sen University,1997,18(4): 4.

[20] 彭积城,蔡金锭.油纸绝缘变压器老化特征分析[J].电子测量与仪器学报，2014,28(7):763. PENG Jicheng,Cai Jinding,Analysis on characteristics of oil-paper insulation transformer[J].Journal of Electronic Measurement and Instrumentation,2014,28(7): 763.

Evaluationonmicrowaterconditionoftransformerinsulationconsideringlineshapefactor

ZHENG Wen-di， CAI Jin-ding， ZENG Jing-lan

(College of Electrical Engineering and Automation，Fuzhou University，Fuzhou 350116，China)

The relation of line shape factor and micro water condition from the perspective of microscopic dynamics is analyzed for damp condition of transformer not being evaluated directly by conventional time domain dielectric response method.The different dielectric polarization processes hidden in the polarization current were resolved individually by the proposed time-differential method.The method not only solved the line shape factor,but also determined the number of relaxations directly.The results on analysis of transformer test curves shows that the damp condition is related to the number of relaxations and line shape factors closely.The larger number of relaxations,the more micro water in the insulation.The damp condition goes worse when line shape factors increase.

oil-paper insulation; transformer; micro water condition; number of relaxation; line shape factor

(编辑：贾志超)

2016-05-26

国家自然科学基金(61174117)；福建省自然科学基金(2017J01480)

郑文迪(1984—)，男，博士，讲师，研究方向为电力设备智能诊断与控制技术； 蔡金锭(1954—)，男，博士，教授，研究方向为电力设备故障诊断； 曾静岚(1990—)，女，硕士，助理工程师，研究方向为变压器绝缘诊断。

郑文迪

10.15938/j.emc.2017.08.005

TM 411

:A

:1007-449X(2017)08-0033-08