接地面积可变的履带驱动机构设计与分析

向 猛，黄晶晶，高立婷，肖名涛，孙松林

（1.湖南农业大学 教育学院，湖南 长沙 410000；2.湖南农业大学 工学院，湖南 长沙 410128）

接地面积可变的履带驱动机构设计与分析

向 猛1，黄晶晶1，高立婷1，肖名涛2，孙松林2

（1.湖南农业大学 教育学院，湖南 长沙 410000；2.湖南农业大学 工学院，湖南 长沙 410128）

为了解决履带式农田作业机械接地面积与通过性的关系矛盾，设计了一种可使接地面积变化的履带驱动机构，通过操控履带变形装置，可改变履带的接地面积，从而使机器在水田作业时增加接地面积防止履带车辆沉陷，在转运或越障时增加接近角、减少履带接地面积提高履带车辆通过性。为了确定履带变形装置的详细参数，建立了履带变形装置的数学模型，设计了基于MATLAB软件的程序，通过仿真分析和优化，论证了履带变形装置的可行性。

履带；履带长度；可变接地面积；MATLAB

履带机构凭借其较大的接地面积、高抗沉陷能力，广泛应用于土质松软、环境复杂等工作环境。可改变接地面积的履带驱动机构，能在越坎爬坡时加大接近角，增强其通过性。在平坦地面做主要工作时，又能调低前后支撑轮的高度，从而增大接触面积，降低接地压力以提高抗沉陷能力。

这种机构在变化时，前后支撑轮会移动位置，因此变形过程中可能会影响其与履带的配合松紧度，而松紧度直接关系到机器的安全与稳定性能，过松会导致履带容易滑脱，过紧则会使变形过大而卡死或断裂。因此优化机构参数，让履带机构在满足接近角、最小接地面积等设计要求的同时，始终有一个合适的松紧度，成了亟待解决的问题。

1 履带变形装置设计

参考以往履带机构的设计，有驱动轮、承重轮与机架等基本组成，又为了实现接地面积可变/接近角可调等功能，选用由液压杆的伸缩推动多杆同时运动，控制前后支撑轮上下移动，使装置的前后接近角变化来实现接地面积的结构来实现。

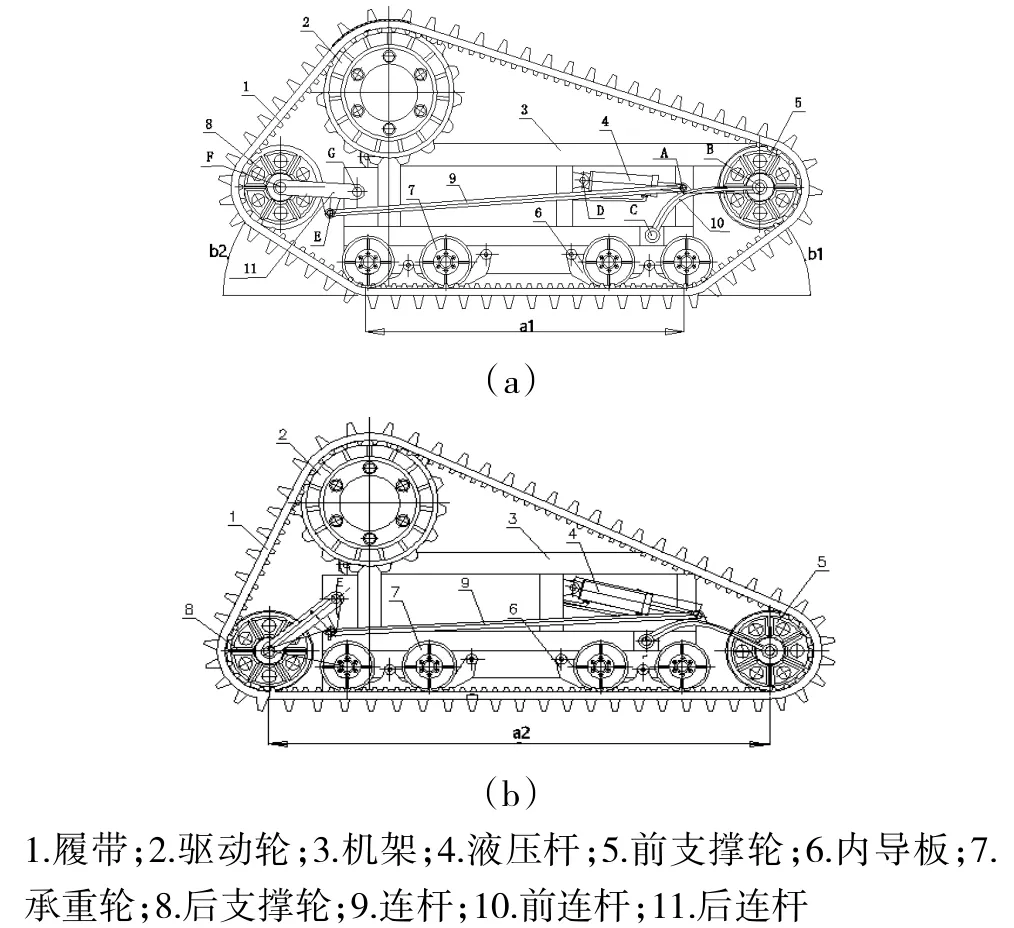
图1 可变接地面积的履带驱动机构图

如图1所示a图为装置变形前，b图为装置变形后。a1、a2表示装置最小与最大接地长度，b1、b2表示装置最大前后接近角。

装置运动原理为：液压杆一端定位于机架上点D，另一端与前连杆、连杆相连于点A。液压杆的伸出缩进控制这两杆同时运动。其中前连杆一端定位于机架上点C，一端与前支撑轮轴孔配合，前连杆运动时控制前支撑轮上下移动。连杆另一端与后连接杆相连于点E，后连杆一端定位于机架上点G，另一端与后支撑轮轴孔配合。在液压杆伸出时，前支撑轮下移，连杆前移且拉动后连接杆绕点G逆时针旋转，使后支撑轮下移。驱动轮定位于机架上方，承重轮定位于机架底部。因为履带包覆在所有轮子外围，所以液压杆的伸长最终使履带驱动机构的接地面积增大，如图1（b）所示。

在平坦或松软环境工作时，液压杆伸长，装置的接地面积增大，提高其抗沉陷能力。在需要越垄过坎爬坡时，液压杆缩短，装置的接近角增到最大，以适应最复杂的环境。而对于一般复杂的环境，则可调节到合适的液压杆长，使得装置的通过性与抗沉陷能力处于合适状态，保证其最佳运动性。

2 建模分析

2.1 多杆机构位置计算

在图2的机构模型图中，点A为坐标原点，点A、点I、点E分别表示后支撑轮、前支撑轮、驱动轮的圆心位置；FG为液压杆，点F与机架固定；JGH为前支撑轮连杆，点J与机架固定，点H为前支撑轮圆心；BG为连杆；BDC为后支撑轮连杆，点D固定于机架，点C为后支撑轮圆心。

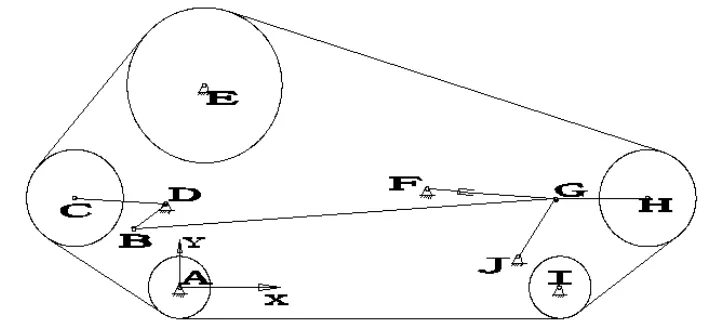
图2 机构模型图

以计算液压杆FG点G为例，设计圆心点F（xF，yF）、点J（xJ，yJ）坐标，以及FG、JG长度后，可用如下两圆相交于两点求交点的方程组求得液压杆FG的点G坐标。

式（1）实际情况会出现两个解，由分析可知取y值大的点。具体matlab程序如下：

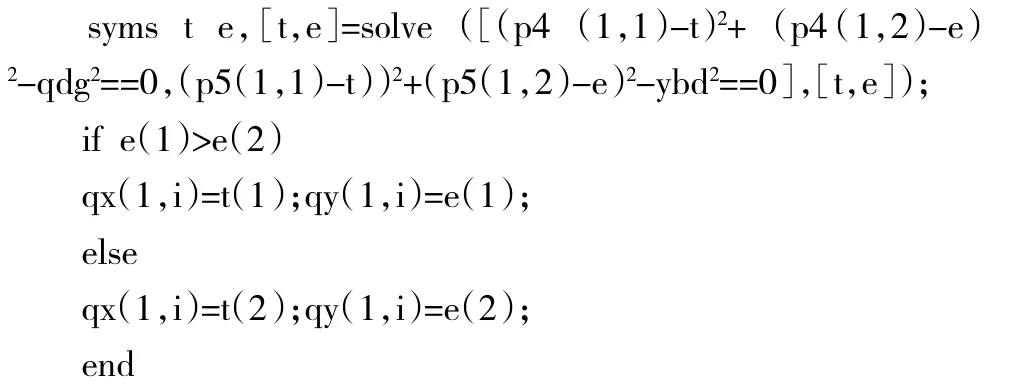
其中：p4为点F坐标；p5为点J坐标；qdg为液压杆长度FG，这是调节量；ybd为JG长度；（qx（1，i），qy（1，i））即所求点；i为程序变量。

最终优化后点G轨迹变化如图3所示（即液压杆伸长过程中的轨迹变化，下同）：

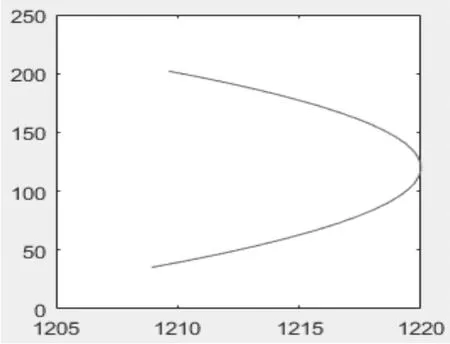
图3 液压杆变动点轨迹

用类似的方法计算出前后两支撑轮圆心轨迹如图4所示：

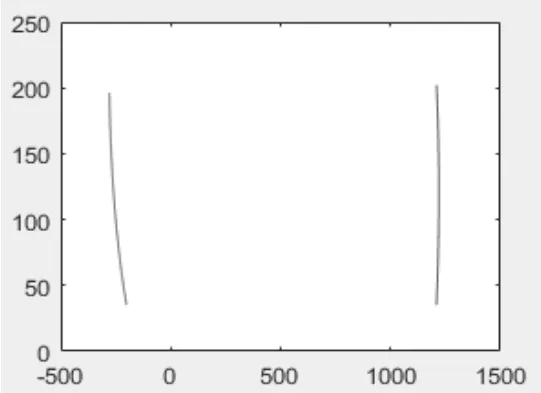
图4 前后两支撑轮圆心轨迹

由图4可以看出，前（蓝）后（红）两支撑轮圆心起始终止时都几乎处于同一水平面上。经后续计算，以及两轮半径相等，得出此两轮在液压杆最长时与底部四个承重轮基本处于同一水平面上，接近理想设计。

2.2 切线长与包线长长度计算

履带是包覆在机构上的，机构四周都是圆轮，而圆轮间的所有切线长与包线长（履带与轮子贴合部分长度）之和，就是履带长。通过以下方法可以计算出后下承重轮包线长，以及其到后支撑轮的切线长：

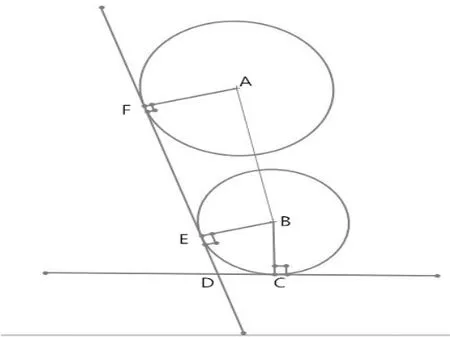
图5 后支撑轮与后下承重轮结构模型图

图5中圆A圆B分别表示后支撑轮与后下承重轮。

图5中公共切线EF同时与AF、BE垂直，得AF//BE，因此有：

EF即切线长。由点A、点B求出AB与CD（水平）的夹角，再由AB与EF求其夹角，两角之和等于角CDF。而圆心角CBE等于180°减去角度CDF，从而可以求出圆弧CE长，也就是包线长。

具体matlab程序如下：

k21=180+atan（（zby（1，i）-p1（1，2））/（zbx（1，i）-p1（1，1）））×（180/pi）；%两圆心倾斜角

d1=norm（p1-［zbx（1，i），zby（1，i）］）；%圆心距

k22=k21+tan（（zbdr-zczr）/d1）×（180/pi）；%切线倾斜角

ld2（1，i）=2×pi×zczr×（（180-k22）/360）；%包线长

ld3（1，i）=sqrt（（zbdr-zczr）2+d12）；%切线长

其中：p1为后承重轮圆心，即点B；（zbx（1，i），zby（1，i））为后支撑轮圆心；zbdr，zczr为后变动轮与承重轮半径；i为程序变量。

经计算得图6数据：

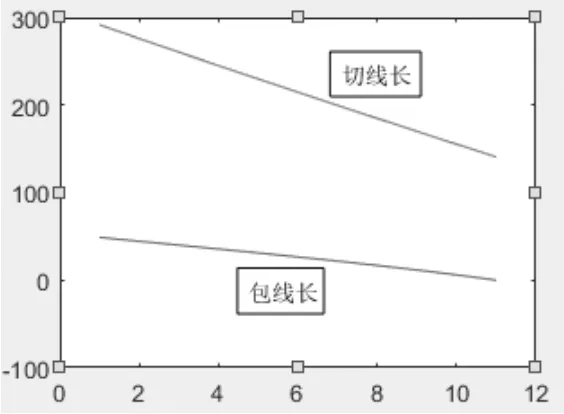
图6 切线长与包线长

从图6可以看出后支撑轮在下降过程中，这一段切线长与包角长都持续下降，并且包线长趋向0，即后支撑轮底部与机构底部趋向水平。

2.3 履带总长计算与分析

履带总长为所有切线长包线长之和。经多次优化设计得出表1数据：

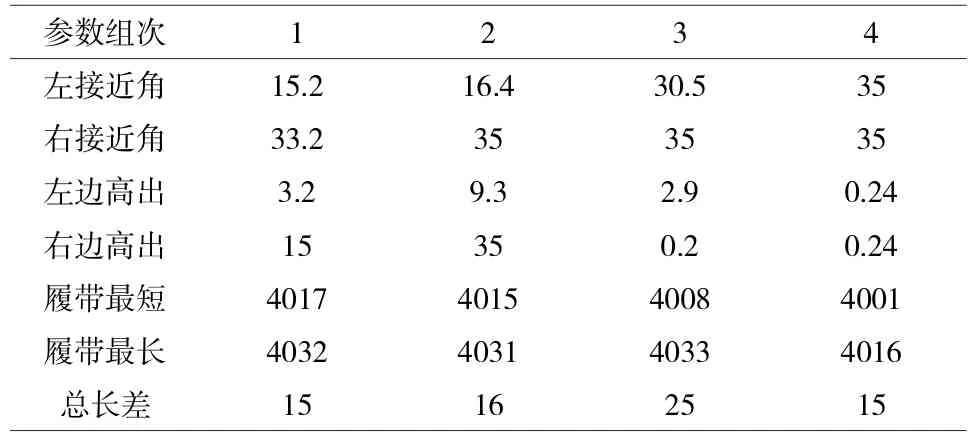
表1 履带总长计算与分析

其中第四组最符合设计要求，具体的履带总长变化如图7所示：

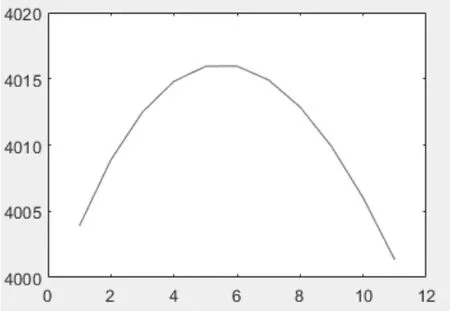
图7 履带总长

在第四组参数时，履带变化总长差为15mm，总长始终略大于4000mm，在选用的履带许可范围内。并且前后最大接近角皆为35°，保证了装置的复杂路面通过性。前后支撑轮最小离地高度皆趋近零，即在履带机构实现最大接地面积时，底面近乎水平，符合设计期望。在履带变形前，装置最小接地长度a1为1040mm，装置变形后接地长度a2为1409.8mm，增加了35.6%。

3 结论

文章通过MATLAB对一种可变接地面积的履带驱动机构进行了数学建模分析，计算出履带长度的变化规律，验证了装置设计的可行性。且通过改变机构参数，优化了结构，使机构在满足设计要求的接近角、最小接地面积等参数时，也保证履带长度在合适的范围内变化，为此机构的设计提供了技术参数。

［1］江创华，刘文强，尚元瑞，等.柔性履带的应用研究［J］.秦皇岛天业通联重工股份有限公司，2010，（10）.

［2］肖名涛，孙松林，黄毅，等.一种可改变接地面积的履带驱动机构［P］.中国专利：CN204567828U,2015-08-19.

［3］项宏伟.便携式可变形履带式机器人的机构设计与运动研究［D］.沈阳：沈阳工业大学，2015.

［4］刘虹玉.微型履带山地拖拉机性能分析与仿真——稳定性、通过性分析与仿真［D］.咸阳：西北农林科技大学，2014.

［5］朱岩，王明辉，李斌，等.履带可变形机器人越障性能研究［J］.机器人ROBOT，2015，（6）.

［6］顾履平.履带拖拉机行走机构的设计［J］.洛阳拖拉机研究所，1984，（3）.

［7］肖永开，李晓雷.高速履带车辆履带预紧张力对平顺性的影响［J］.计算机仿真，2006，（7）.

［8］肖名涛，孙松林，罗海峰，等.双平行多杆栽植机构运动学分析与试验［J］.农业工程学报，2014，（17）.

湖南省科技厅重点研发计划项目（2015NK2006，2016NK2111）。

向猛（1993-），男，大学本科，主要从事农业机械设计与研究工作。

肖名涛，副教授，主要从事农业机械研究工作。