中国金融业不同板块间风险传导的非对称性研究——基于非对称MVMQ-CAViaR模型的实证分析

曾裕峰，简志宏，彭 伟

(1. 复旦大学经济学学院，上海 200433；2. 华中科技大学经济学院，湖北 武汉 430074；3.中南财经政法大学，湖北 武汉 430073)

中国金融业不同板块间风险传导的非对称性研究
——基于非对称MVMQ-CAViaR模型的实证分析

曾裕峰1，简志宏2，彭 伟3

(1. 复旦大学经济学学院，上海 200433；2. 华中科技大学经济学院，湖北 武汉 430074；3.中南财经政法大学，湖北 武汉 430073)

针对原始MVMQ-CAViaR模型未考虑正负冲击具有非对称性的不足，本文将其扩展为非对称MVMQ-CAViaR模型和联合非对称MVMQ-CAViaR模型，继而运用该模型分析了我国金融业不同板块间的风险传导效应，并采用严谨的后测检验对比了各个模型的预测效果。结果表明，银行对证券和保险板块均具有显著的风险传染效应，而证券只能单方向地吸收其他板块的风险溢出；正负信息冲击对自身以及其他板块存在不同程度的非对称特征，且指数下跌对VaR的影响效果要强于指数上涨，联合负向冲击会放大原有的风险水平；新构建的两个非对称模型能显著提升原有模型风险预测精度，其中联合非对称MVMQ-CAViaR模型的预测效果更佳。

风险传导；MVMQ-CAViaR模型；非对称性；系统性风险

1 引言

2012年以来，我国金融体制改革进一步深化，监管层逐步放松对金融的管制，特别是利率市场化改革对我国金融机构带来两方面最直接的影响:一是促进传统金融机构从单一存贷、保费等业务向多种创新业务盈利模式转变，并通过金融机构的并购、重组等手段促进目前以分业经营为主的金融体制逐渐转向混业经营改变；二是推动各类金融创新和金融衍生产品的快速发展，将银行、证券公司和保险公司等不同类型的市场参与主体联结得更加紧密。金融领域这种重大改变所带来金融服务业务广泛的关联性和交叉性使得系统性金融风险大大增强。我国现阶段系统性金融风险日益凸显，而相关市场主体的风险防范意识相对淡薄且风险管理水平较弱。我国金融市场哪个板块对其他市场的传染效应最强？哪个板块对整体金融风险的贡献最为巨大？以及金融系统内部风险传导规律及内在机制如何？回答这些问题不仅有利于投资者根据板块的关联性做出最优的投资组合决策，而且为政策制定者和市场监管者如何更有效防范系统性风险提供了理论依据和实践指导。

不同行业(或者不同市场)之间风险传染都有着内在的传递机制和经济基础，关于金融业不同板块间的风险传导关系主要依据以下两个渠道：(1)金融机构间复杂的业务往来和信贷关联：金融机构之间在存款、信贷和支付体系上相互联结, 一家金融机构的倒闭势必会引起与之有业务关联的金融机构发生支付困难,如果其自有资本不能补偿损失, 则同样将面临倒闭风险,通过这种链式反应(Chain Reaction)不断传递，从而引发整个金融体系发生大范围的违约和倒闭事件[1]；(2)心理预期的变动引发投资者恐慌和信心的崩溃：当单个金融板块发生金融困境时，由于信息的不对称，投资者会依据一个板块的价格变化去预测其它板块指数的价格走势，为了尽量避免损失，投资者将会提前进行撤资来满足自我的流动性偏好，最终对其具有关联度的板块也造成了严重冲击[2-3]。特别地，在我国中小投资者占绝对比例，投资者显著的“投机心理”和“羊群效应”会强化第二个渠道的影响效果。

国内外关于市场风险传导的文献相对详尽，其中主要集中在收益率的一阶矩[4]和二阶矩[5]层面上，且大部分文献探讨的对象主要是股票市场和汇率市场[6]、股票市场和债券市场[7]、股票市场和石油市场[8]等不同市场之间的风险传导。近年来，部分学者开始关注金融机构和金融板块的系统性风险传导话题，其中贾彦东[9]基于我国银行2007-2010年明细的支付结算数据，将金融网络结构因素纳入到对系统性风险的测度中，以此估算出我国金融机构对整个市场的“直接贡献”和“间接参与贡献”以及系统重要性排序。欧阳红兵和刘晓东[10]采用最小生成树(MST)和平面极大过滤图(PMFG)方法有效地识别出金融网络中节点的重要性，且MST的唯一性可以确保全面和直观地显示系统性风险的潜在传导路径。陈建青等[3]基于静态CoVaR模型和“滚动窗口”的动态CoVaR模型分别探讨了我国银行、证券和保险板块之间的系统性金融风险的溢出效应，研究发现金融不同板块间的溢出效应具有正向性和非对称性。Billo等[11]采用主成分分析和格兰杰因果网络方法分析了美国四个金融部门的复杂网络关系，发现它们近年来彼此高度相互关联，并且银行市场的冲击对整体金融系统的影响最强。White 等[12]首次提出多元多变量条件自回归风险价值即(MVMQ-CAViaR)模型，并分析了单个金融机构与整个金融系统的风险溢出效应。然而该模型忽略了市场冲击项对VaR的非对称影响。

非对称性被视为金融市场中最重要的典型事实之一，是指金融市场在遭遇信息冲击时，好消息和坏消息对股价波动的影响效果不一致[13]。该性质在金融建模过程中得到了广泛应用。Li 和Zou[5]运用非对称的DCC-MGARCH研究了中国政策的转变对股债关系的影响，研究发现股债相关关系在受到联合负向信息冲击时显著增强，而上证和深圳股票相关系数在受到联合正向冲击时趋于变大。Beber和Brandt[14]研究也发现，在不同类型的信息冲击和不同的商业周期阶段中，金融机构的资产回报呈现显著的不对称性，其中在经济扩张阶段遭受的负向冲击影响最大。陆蓉和徐龙炳[15]采用EGARCH实证研究我国股票市场在牛市和熊市阶段对“利好”与“利空”的不平衡性反应特征，并从投资者预期、投资者结构和交易机制等方面解释这种非对称性产生的原因。刘庆富和周程远[13]构造了非对称门限随机波动模型去检测重大风险事件对我国股票市场影响的杠杆效应。文凤华等[16]同时考虑市场波动的杠杆效应和价量关系，发现新构造的LHAR-RV-V模型能改善对已实现波动率的预测精度。非对称性在VaR的建模上同样非常重要，Engle和Manganelli[17]在提出最原始CAViaR模型时就考虑到市场冲击项对VaR潜在的非对称效应，因此在提出SAV模型的同时也给出了具有非对称性质的AS模型。López-Espinosa等[18]为研究个体金融机构和金融系统之间非线性的尾部联动时提出了非对称的CoVaR模型，发现国际银行的正负收益冲击对金融系统的影响并不相同。简志宏和彭伟[19]在SAV模型和AS模型的基础上构造了隔夜-SAV模型和隔夜-AS模型，研究表明美元走弱对这三个市场隔夜风险影响大于美元走强所带来的影响。

总体而言，现有文献主要集中探讨了收益率均值和波动率的杠杆效应，但自Engle和Manganelli[17]提出CAViaR模型以来，非对称性在VaR度量上也得到了重要的运用。为了将非对称的性质引入到多元分位数回归模型中，我们首先将对称的MVMQ-CAViaR模型扩展为非对称的MVMQ-CAViaR模型，探讨了正向冲击和负向冲击对VaR影响效果的差异，这是本文的第一个贡献。同时考虑到联合负向冲击可能是市场中的共同冲击(Common Shock)，这种冲击会被市场过度反应，最终可能具有一定的放大效果，所以本文进一步将其扩展为联合非对称MVMQ-CAViaR模型，这是本文方法论上第二个贡献。另外，本文通过分位数脉冲响应函数探讨了不同板块单独或同时出现正负信息冲击时，对不同市场风险影响的动态变动过程，有益于我们更清晰地辨别不同金融板块在整个系统中风险传导重要性。这是本文第三点贡献。

2 研究方法简介

2.1 实证模型

Engle和Manganelli[17]认为市场的波动率与风险价值成正相关关系，而金融市场中股价存在显著的波动聚集效应，那么与波动率密切相关的风险价值也应具有类似的性质。为此，作者在分位数回归思想的基础上，提出具有自相关特征的CAViaR(Conditional Autoregressive Value at Risk)模型直接对金融市场的风险价值进行度量。然而，CAViaR模型主要适用于分析单个板块(或单个市场)的动态风险特征，却无法捕捉不同板块(或不同市场)之间风险相互传染的复杂关系。为克服上述模型的不足，White 等[12]将传统的CAViaR模型扩展成为MVMQ-CAViaR模型，该模型将单方程的分位数回归思想扩展到向量自回归的结构化方程，并揭示了单个板块(或单个市场)的风险价值不仅受到本身市场的影响，还受到其他市场的风险溢出，市场之间是相互影响、相互传染的。具体表达式如下：

(1)

其中，qit(θ)表示市场收益率Yit-1在θ概率下的条件分位数，也可看作为市场收益率对应θ概率的风险价值VaR。|Yit-1|表示市场指数i的收益率绝对值，该项代表市场冲击项，且暗含滞后一期的正向冲击和负向冲击对当期VaR具有相同的影响效果。qit-1代表滞后的条件分位数，它能很好地描述金融市场尾部分布的自相关性。以银行板块和证券板块为例，假设q1t代表银行的VaR，而q2t代表证券的VaR，式(1)表明了银行的风险价值q1t不仅受到了自身市场的影响，还受到证券板块的极端风险q2t-1和市场冲击项|Y2t-1|的影响。

模型(1)假设市场冲击项不具有“杠杆效应”，换言之，本市场和其他市场的正向冲击和负向冲击对风险价值的影响效果是等价的，现实生活中投资人效用函数中常对损失带来的负效用施以更大的权重，对收益带来的正效用给予较小权重，所以本文将(1)式扩展为非对称MVMQ-CAViaR模型，模型表达如下：

(2)

其中，(Y1t-1)+和(Y1t-1)-分别表示滞后一期收益率的正部和负部。当两个板块同时出现负向冲击时，此时的冲击很可能是共同冲击，这种冲击将会破坏公众投资信心，投资者的恐慌心理将会进一步放大原有的市场风险，为了更深入地研究不同金融板块同时受到负向冲击时对VaR的非对称效应，同时通过借鉴Li和Zou[5]对联合负向冲击的多元GARCH模型的建模思路，我们将模型(2)进一步扩展成为联合非对称MVMQ-CAViaR模型，具体模型表示如下：

(3)

2.2 分位数脉冲响应分析

由方程(1)-(3)可知，金融行业不同板块间的风险会相互传导，单个市场的市场冲击项(即Yit)会直接影响到自身和其他市场的风险价值。一般而言，当期的市场冲击会改变投资者对未来一期金融资产风险价值的预期，进而直接导致VaRt大小的变化。另外，由于市场中的资金可以在不同行业中自由地流动，投资者会根据风险状况的变动改变其在不同板块间的投资组合，这种板块的联动效应将间接引起其他市场VaRt的变化。为了考察变量之间互动的更为清晰的方法是脉冲响应分析，传统的脉冲响应分析主要探讨市场信息冲击对收益率的均值影响，而本文需要考察的是市场冲击对收益率尾部的动态影响过程，因此采用的是White等[12]最新提出的分位数脉冲响应分析(Quantile Impulse Response Function，即QIRF)。该方法的具体计算步骤如下：

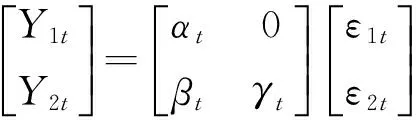
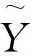
最后，根据不同板块的冲击得出ΔYit值，并由模型(1)-(3)估计出的系数值进一步分析其对不同板块的风险价值VaR的动态影响过程。

2.3 模型的估计方法

MVMQ-CAViaR模型属于多元分位数回归范畴，可采用最小绝对离差法(Least Absolute Deviation，LAD)估计，它需要优化的目标函数为：

(4)

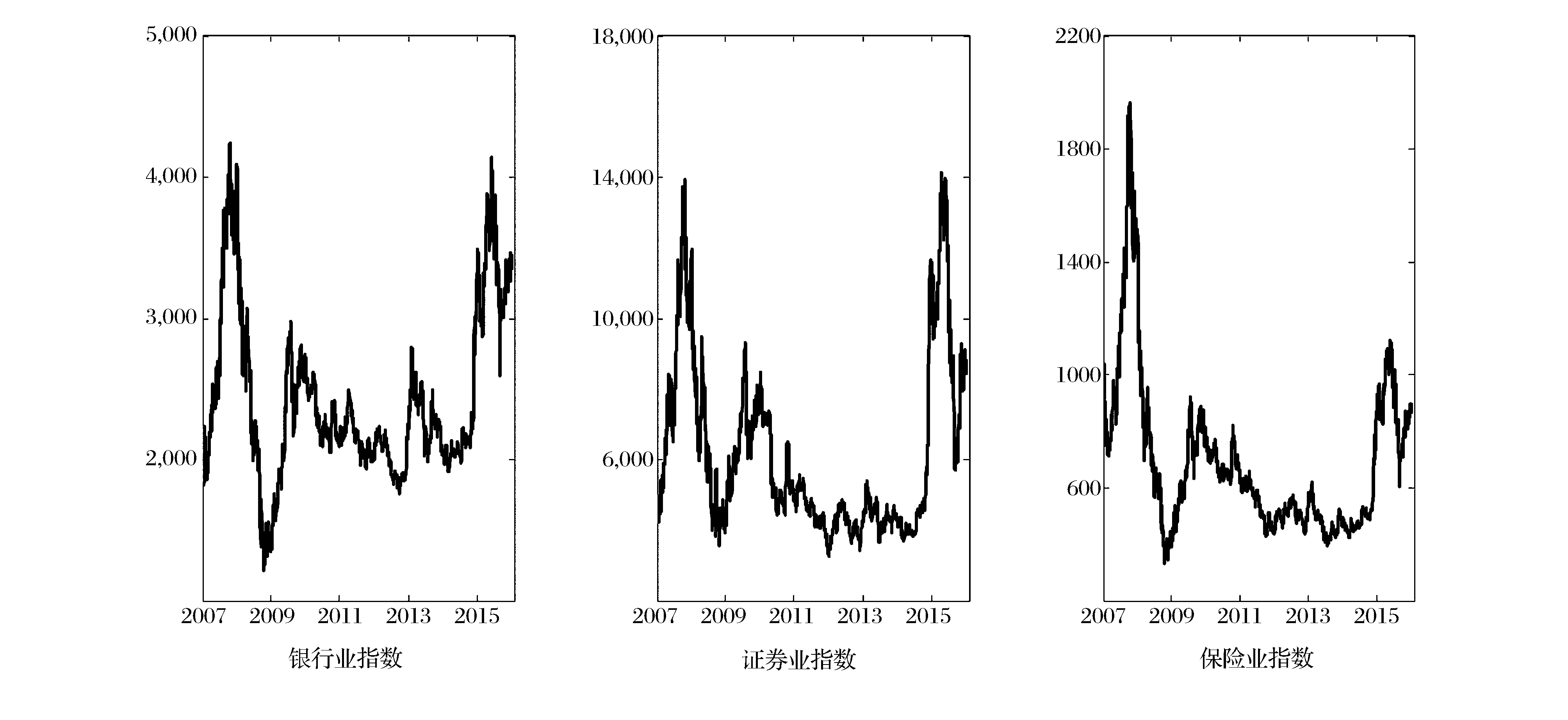
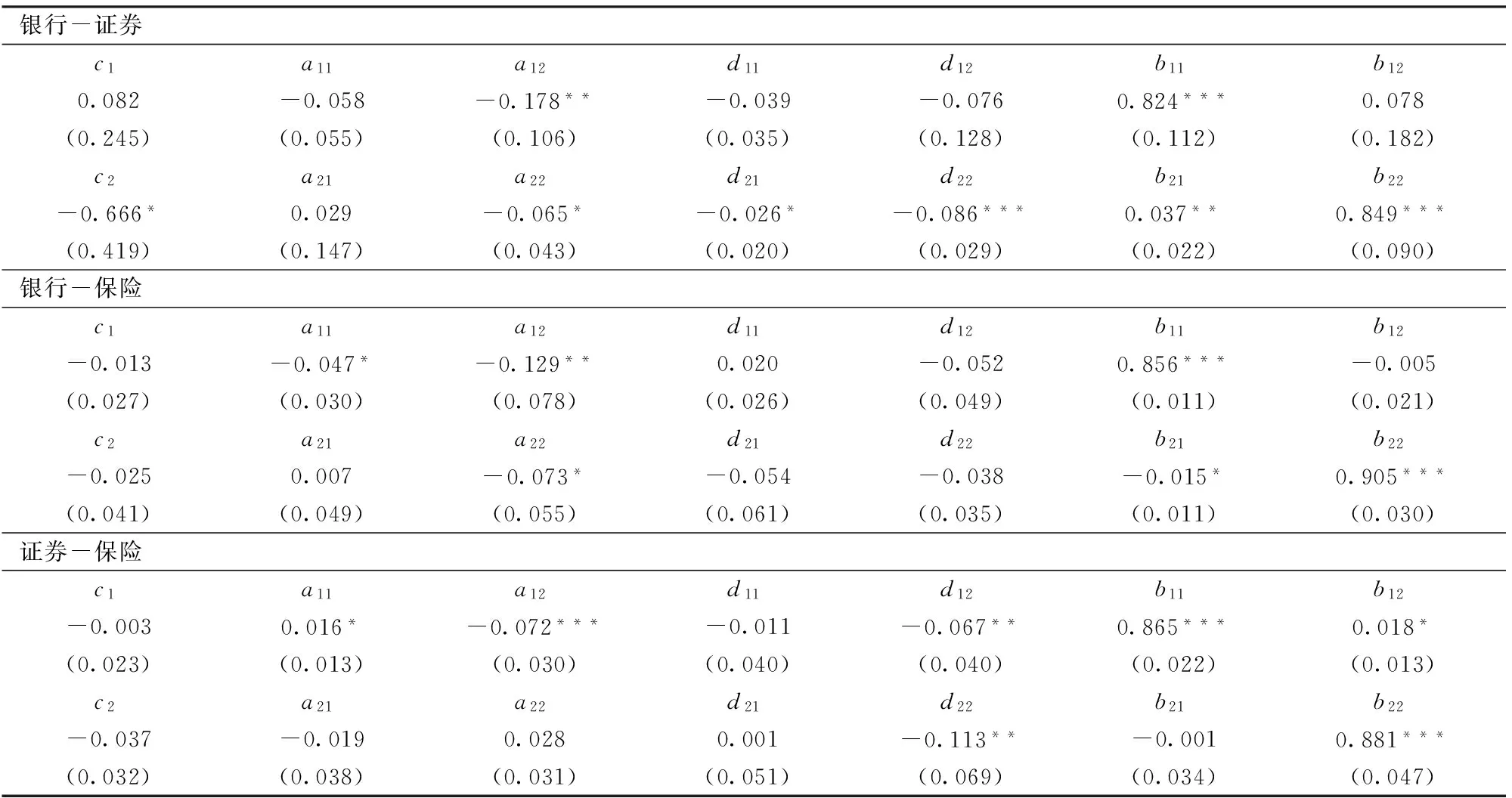
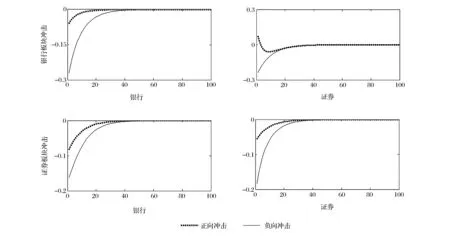
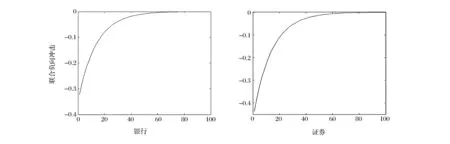
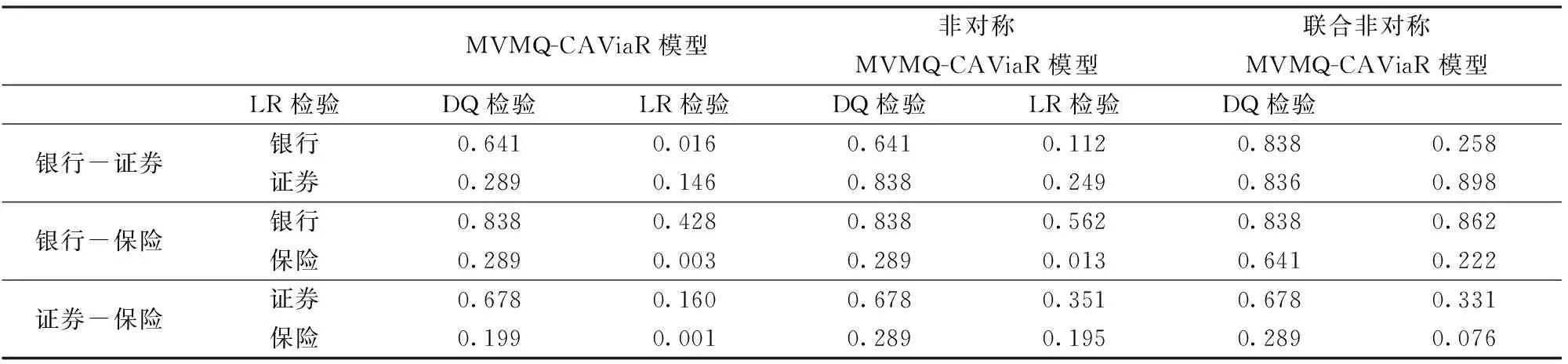
其中，ρ(θi)=θi-I(Yit

本文以金融业不同板块指数在θ=5%的条件分位数为例,取前100个观测值对应的分位点来初始化qi1，并运用单纯形算法(Simplex Algorithm)和拟牛顿算法(Quasi-Newton Method)对模型进行优化。为提高结构化模型的估计效率，本文采用了两步估计法：第一步，首先估计Engle和Manganelli[17]提出的单变量分位数SAV(Symmetric Absolute Value)模型，并将其估计的结果作为第二步优化的初试估计系数；第二步，对多元分位数模型(1)-(3)进行整体优化，使目标函数(4)达到最小化。具体估计步骤可参考White等[12]的文献。

2.4 模型稳健性检验方法

模型的样本内表现并不能简单地扩展到样本外，为了进一步论证该模型预测VaR的效果，还必须进行样本外的稳健性检验。Kupiec[20]假设该模型能有效地预测风险，进一步证明了“击中事件”序列服从贝努利分布，并构造似然比的非条件检验统计量：

(5)

其中，p为显著性水平，N为预测的样本总数，n为预测样本中的击中次数。当LR统计量大于给定置信水平下卡方分布的临界值，则拒绝原模型。相反，当统计量小于临界值，则接受该模型。

通过(5)式可知到Kupiec 似然比检验量是刻画实际击中次数接近理论击中次数程度的指标。进一步的研究表明，除了检验失败比率以外，还应检验击中事件是否存在相关性，如果发生VaR预测失败的观测值之间具有明显的相关性，那么有可能发生连续超过VaR的损失，这将给投资者带来巨大的损失，也就是说，精确可靠的风险测度模型的击中序列应该是无偏并且无自相关的。由此，Engle和Manganelli[17]提出了动态分位数检验(Dynamic Quantile test，DQ test)，以多头风险为例，该检验首先定义一个新的击中序列：

HITθ,t=I(yt<-VaRt)-θ

(6)

其中，θ为给定的分位数，当yt<-VaRt时，HITθ,t=1-θ；当yt>-VaRt时，HITθ,t=-θ。显然，如果模型参数估计正确，那么E(HITθ,t|Ωt-1)=0。这说明HITθ,t对于任何滞后的HITθ,t-k以及预测的VaRt-k都应不具备相关性，构造如下回归方程：

HITθ,t=β0+β1HITθ,t-1+β2HITθ,t-2+……+βpHITθ,t-p+βp+1VaRt+ut

(7)

把上述模型表述成矩阵形式：HITθ,t=Xβ+ut，其中X是T×K矩阵向量，取p=5,k=7。在原假设：β=0的情况下，构造的DQ检验统计量为：

(8)

3 实证结果与分析

3.1 数据来源及描述性统计

本文选取了申银万国二级行业指数中的银行业、证券业以及保险业三个板块的指数作为原始数据，由于保险业指数于2007年1月17日才正式公布，所以本文以2007年1月17日为起始日，以2015年12月29日为结束日，共获得2176个有效的日频率收益率数据，所有数据均来源于Wind数据库。为了检验本文所使用模型的稳健性，整个数据样本划分为样本内和样本外，其中前1676个数据样本用于拟合实证模型，最后500个数据用于样本外的回测检验。

由表1的结果可知，在本文所选的样本区间内，银行和证券的平均收益率均为正值，其中证券平均收益率达到0.033，而保险业却为负值，如果股价指数的变动反映了该行业经营业绩的整体预期，从这个角度而言证券业要比保险业发展的更为景气，同时证券板块的标准差相对最大，即它的波动最为剧烈，高风险同时带来了更高的风险溢价，符合金融学中的“小盘股效应”；三个板块指数均具有“负偏”和“尖峰厚尾”的典型特征；最后根据J-B统计量和ADF统计量的P值，进一步发现所以指数收益率均是非正态的平稳时间序列。

图1给出了三个板块指数的价格走势图，整体而言，银行、证券和保险的走势基本保持一致。具体而言，2007年1月到2007年10月，我国A股市场经历了有史以来最大的牛市行情，金融行业三大板块在大盘的驱动下快速地拉升达到顶峰；2008年受美国金融危机的波及，我国股市开始断崖式下跌，截至2008年9月，三个板块平均跌幅达到65%以上，其中保险板块跌幅最大；随后一直处于震荡箱型轨道，直到2014年6月，受益于政策的改革红利、充足的货币流动性以及舆论媒体的鼓吹，推动着我国股票市场进入了疯牛状态，但牛市背后所潜藏的杠杆交易过度滥用、场外证券活动缺乏监管的风险，再次让预期的慢牛市成为泡影。

3.2 MVMQ-CAViaR模型估计结果

表2分别给出了银行和证券、证券和保险以及银行和保险在5%分位数水平下相互之间的风险传导结果，总体而言，所有的系数b11和b22均在1%显著性水平下拒绝原假设，且系数值均大于0.8，说明金融不同板块风险水平都具有高度的序列相关性，其他具体结果如下：

第一，在银行和证券的多元回归模型中，系数a11达到了10%的显著性水平，说明银行前期收益率对VaR具有显著的负向影响，系数a22也显著异于零，说明证券板块的市场冲击同样会加大市场的风险值。另外，我们还发现系数a21和b21也达到了10%的显著性水平，表明银行板块的极端风险和市场冲击会传导到证券板块，且影响方向为负。但是证券板块对银行板块却不具有显著的风险传导效应。

第二，针对银行和保险的回归结果，可发现系数a22在统计意义上并不显著，说明保险板块风险并不受到前期市场冲击项的影响，系数a21显著，表明银行的极端风险会传递到保险板块，而保险行业的风险未能传染到银行。

第三，至于证券和保险之间的实证结果，可以看出保险的极端风险对证券具有显著的单向溢出效应，而证券不具备主动传导风险的功能。

总之，银行对证券和保险均具有显著的风险传导效应，而其他板块对银行却不具有风险溢出。可能是由于我国金融体系中银行具有绝对主导地位，与其他金融机构之间业务合作相对更复杂和密切，而且银行体系本身的预防机制和风险防范制度相对更完善，因此它与其他板块的风险传导具有明显的非对称性。而证券处于从属地位，这可能与国内很多券商资产规模相对较小，且部分券商为银行或企业集团的全资子公司有密切关系。

表1 样本的描述性统计结果

注：正态分布的JB检验和平稳性的ADF检验均给出的是该统计量的P值，P值越小，以更大的可能性拒绝原假设。

图1 金融行业不同板块的价格走势图

银行-证券c1a11a12b11b12-0.013-0.106*-0.0280.952***0.011(0.162)(0.080)(0.040)(0.161)(0.142)c2a21a22b21b22-0.042-0.042*-0.089**0.041**0.960***(0.131)(0.033)(0.048)(0.022)(0.114)银行-保险c1a11a12b11b120.005-0.091**-0.0070.961***0.003(0.035)(0.050)(0.033)(0.028)(0.027)c2a21a22b21b22-0.013-0.039-0.0470.022**0.973***(0.033)(0.041)(0.045)(0.012)(0.029)证券-保险c1a11a12b11b12-0.006-0.068**-0.0530.949***0.031**(0.031)(0.038)(0.068)(0.082)(0.023)c2a21a22b21b22-0.0220.010-0.0870.0220.934***(0.037)(0.043)(0.083)(0.133)(0.179)

注：括号内数据是对应系数的标准误，*、**、***分别表示在10%、5%和1%的显著性水平下拒绝原假设。以下表述方式类似。

3.3 非对称的MVMQ-CAViaR模型估计结果

表2并未区分板块指数上涨和下跌对VaR的不同效果。为进一步探讨金融行业VaR的杠杆效应，表3给出了非对称MVMQ-CAViaR模型的实证结果，可以看出三个多元分位数回归模型的估计结果与表2基本是保持一致，主要的差异体现在非对称系数上。由系数a11、a12和d21、d22的显著性易知，银行板块的风险受到自身负向市场冲击的显著影响，而正向市场冲击影响的并不完全显著；证券板块则同时受到正向、负向市场冲击的显著影响；另外保险板块主要也偶尔会受到负向市场冲击的作用。并且所有参数的绝对值并不对应相等，这意味着我国金融行业的市场冲击对不同板块的VaR具有明显的非对称效应，且板块指数下跌所带来的冲击要大于板块指数上涨。再由系数a21、a22和d11、d12估计结果可以看出，银行的负向市场冲击会传染到证券板块和保险板块，并显著地加大这两个板块的风险价值，而正向市场冲击系数均不显著；保险的负面信息也会传染到证券板块，证券则处于一个相对被动的地位，不存在对其他市场的风险溢出效应。

联合非对称MVMQ-CAViaR模型在非对称MVMQ-CAViaR模型基础上引入了联合负向信息冲击项，由系数e1的显著性可知，当前期银行和证券同时出现负向市场冲击时，类似与“共振”的作用效果，这种冲击会显著地增加下一期两个市场的风险；同样地，银行和保险同时出现负向冲击时，也会进一步放大原有市场的VaR；然而，证券和保险的联合负向冲击却不具有统计意义上的显著效果。

图2和图3分别给出了银行和证券板块的分位数脉冲响应结果，限于篇幅，其他板块的QIRF结果备索。无论是源于银行板块还是证券板块的一个标准差信息冲击，发现负的信息冲击对原有市场的影响强度要大于正的信息冲击，且这些冲击大概持续到40期左右慢慢衰减为0。值得一提的是，银行板块的正向冲击对证券的初期影响效果为正，然后快速衰减为负。对比图2和图3可以清晰发现，当出现联合负向信息冲击时，这种冲击的强度要显著大于单个市场的负向冲击,而且波动性较大的证券板块风险扩大值要明显大于银行。

表3 非对称MVMQ-CAViaR模型的估计结果

图2 银行和证券板块市场冲击的脉冲响应过程 注：图2上半部分给出了银行板块受到1个单位标准差新信息冲击时，对银行和证券未来100期的反应；同理，下半部分是证券板块受到1个单位新信息冲击时，对银行和证券未来100期的反应。

银行-证券c1a11a12d11d12e1b11b120.001-0.040-0.173*-0.032-0.053-0.081*0.847***-0.013(0.045)(0.053)(0.120)(0.033)(0.056)(0.066)(0.023)(0.015)c2a21a22d21d22e2b21b22-0.0130.004-0.178***-0.012-0.062*-0.123**-0.028**0.851***(0.034)(0.045)(0.047)(0.025)(0.048)(0.074)(0.016)(0.017)银行-保险c1a11a12d11d12e1b11b12-0.001-0.035**-0.134***0.015-0.072-0.078**0.839***-0.024*(0.034)(0.020)(0.044)(0.020)(0.033)(0.050)(0.009)(0.016)c2a21a22d21d22e2b21b22-0.0320.013-0.093*-0.022*-0.046-0.095*-0.023**0.820***(0.033)(0.029)(0.062)(0.017)(0.058)(0.071)(0.011)(0.013)证券-保险c1a11a12d11d12e1b11b12-0.0210.023*-0.075**-0.030-0.084**0.0030.869***-0.016*(0.040)(0.015)(0.041)(0.048)(0.045)(0.013)(0.060)(0.011)c2a21a22d21d22e2b21b22-0.004-0.080-0.0400.106-0.140*-0.0110.0930.862***(0.109)(0.062)(0.090)(0.095)(0.084)(0.033)(0.090)(0.092)

总之，这部分从回归结果的系数值以及分位数脉冲响应两种方法很好地阐述了我国金融业不同板块之间风险传导的显著非对称性，进一步还发现我国银行对其他板块具有显著风险传染效应，而证券则处于被动接收其他板块风险的不利地位。

图3 银行和证券联合负向冲击的脉冲响应过程 注：图3给出了银行板块和证券板块同时受到1个单位标准差新信息冲击时，对银行和证券未来100期的反应。

MVMQ-CAViaR模型非对称MVMQ-CAViaR模型联合非对称MVMQ-CAViaR模型LR检验DQ检验LR检验DQ检验LR检验DQ检验银行-证券银行0.6410.0160.6410.1120.8380.258证券0.2890.1460.8380.2490.8360.898银行-保险银行0.8380.4280.8380.5620.8380.862保险0.2890.0030.2890.0130.6410.222证券-保险证券0.6780.1600.6780.3510.6780.331保险0.1990.0010.2890.1950.2890.076

注：黑色字体表示在95%的置信水平下拒绝原模型。表中数据为VaR似然比检验和DQ检验的P值，P值越大，表明该模型计算的VaR精确度越高。

3.4 模型的稳健性检验

表5给出了在5%分位数下不同板块的回测检验结果，可以发现：在5%的显著性水平下，三个模型的Kupiec似然比结果均通过了稳健性检验，但从预测的准确度来看，非对称MVMQ-CAViaR模型要明显优于原始的MVMQ-CAViaR模型，进一步，联合非对称MVMQ-CAViaR模型又要略优于非对称MVMQ-CAViaR模型；另外，从DQ检验来看，传统模型出现了3次拒绝原假设的结果，而非对称MVMQ-CAViaR模型拒绝原假设仅1次，联合非对称MVMQ-CAViaR模型则完全通过了统计意义上的DQ检验。总之，本文新提出的两个模型能显著地提高金融不同板块风险的预测准确性，且联合非对称MVMQ-CAViaR模型相对更有竞争优势，说明对市场冲击项进行杠杆分解具有理论依据和实践意义。

4 结语

为检验收益率市场冲击项对我国金融业不同板块VaR的非对称效应，本文将White等[12]最新提出的多元分位数模型(即MVMQ-CAViaR模型)进行两步扩展，使其成为能刻画市场冲击具有杠杆效应的非对称MVMQ-CAViaR模型和联合非对称MVMQ-CAViaR模型，并运用Kupiec似然比检验和动态分位数检验对模型的预测效果进行评估，主要得出的结论有：银行、证券和保险板块的VaR均具有高度显著的自相关特征，且三个板块指数的整体走势具有较强的一致性；从极端风险溢出的角度而言，银行板块的极端风险会显著地向证券和保险板块进行传染，保险板块的极端价格变动也会引发证券和银行风险水平的变动；从市场冲击项的角度来看，三个板块自身的市场冲击均具有一定程度的杠杆效应，同时银行板块的市场冲击会传递到证券板和保险板块，从而加大其他市场的VaR值，保险板块时常也会对证券板块产生市场冲击，证券板块则只能单方向地被动接收源于其他板块的市场冲击；当不同市场同时发生负向信息冲击时，此时对市场具有“共振”的效果，会进一步加大原来的市场风险水平。

本文的相关研究结论对如何防范我国系统性金融风险具有重要的政策含义，首先，对不同系统重要性的金融机构进行差异化监控和防范。银行在我国整个金融体系具有举足轻重的地位，监管层要重点强化银行相关风险状况的披露制度，加强银行财务信息的透明度。其次，以全局观念来看待我国整个金融系统的风险，强化宏观审慎的监管要求，建立好不同行业间共同应对风险的预警体系。从分业经营慢慢转变为混业经营已成为当前金融业发展的趋势，监管部门和金融机构应积极做好相关的制度安排以减少板块风险联动所带来的负面冲击。最后，要重点监测金融业不同板块同时发生负面消息时对整个金融系统的影响，局部风险的影响相对较小，但不同金融板块同时出现风险事件会严重破坏公众的投资信心，容易造成市场的恐慌心理，从而会剧烈地扩大市场的风险水平。

[1] Kaufman G G, Scott K E. What is systemic risk, and do bank regulators retard or contribute to it?[J]. Independent Review, 2003, 7(3): 371-391.

[2] Kupiec P, Nickerson D. Assessing systemic risk exposure from banks and GSEs under alternative approaches to capital regulation[J]. The Journal of Real Estate Finance and Economics, 2004, 28(2-3): 123-145.

[3] 陈建青,王擎,许韶辉. 金融行业间的系统性金融风险溢出效应研究[J]. 数量经济技术经济研究,2015, (9): 89-100.

[4] Forbes K J, Rigobon R. No contagion, only interdependence: measuring stock market comovements[J]. The Journal of Finance, 2002, 57(5): 2223-2261.

[5] Li Xiaoming, Zou Liping. How do policy and information shocks impact co-movements of China’s T-bond and stock markets?[J]. Journal of Banking & Finance, 2008, 32(3): 347-359.

[6] Lee C H, Doong S C, Chou P I. Dynamic correlation between stock prices and exchange rates[J]. Applied financial economics, 2011, 21(11): 789-800.

[7] 胡秋灵,马丽.我国股票市场和债券市场波动溢出效应分析[J]. 金融研究,2011,(10): 198-206.

[8] 李素芳,朱慧明,李荣. 基于贝叶斯机制转换协整模型的石油——股市非对称效应研究[J]. 中国管理科学,2015,23(9): 46-54.

[9] 贾彦东. 金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J]. 金融研究,2011,(10): 17-33.

[10] 欧阳红兵,刘晓东. 中国金融机构的系统重要性及系统性风险传染机制分析——基于复杂网络的视角[J]. 中国管理科学,2015,23(10): 30-37.

[11] Billio M, Getmansky M, Lo A W, et al. Econometric measures of connectedness and systemic risk in the finance and insurance sectors[J]. Journal of Financial Economics, 2012, 104(3): 535-559.

[12] White H, Kim T H, Manganelli S. VAR for VaR: Measuring tail dependence using multivariate regression quantiles[J]. Journal of Econometrics, 2015, 187(1): 169-188.

[13] 刘庆富,周程远.中国股票市场的非对称效应研究[J].系统工程学报,2012,27(5): 648-655.

[14] Beber A, Brandt M W. When it cannot get better or worse: The asymmetric impact of good and bad news on bond returns in expansions and recessions[J]. Review of Finance, 2010, 14(1): 119-155.

[15] 陆蓉,徐龙炳.“牛市”和“熊市”对信息的不平衡性反应研究[J]. 经济研究,2004,(3): 65-72.

[16] 文凤华,刘晓群,唐海如,等. 基于LHAR-RV-V模型的中国股市波动性研究[J]. 管理科学学报,2012,15(6): 59-67.

[17] Engle R F，Manganelli S. CAViaR: Conditional autoregressive value at risk by regression quantile[J]. Journal of Business and Economic Statistics, 2004, 22(4):367-381.

[18] López-Espinosa G, Moreno A, Rubia A, et al. Short-term wholesale funding and systemic risk: A global CoVaR approach[J]. Journal of Banking & Finance, 2012, 36(12): 3150-3162.

[19] 简志宏,彭伟. 基于CAViaR模型的汇率隔夜风险研究[J].中国管理科学,2015,23(6): 17-24.

[20] Kupiec P H. Techniques for verifying the accuracy of risk measurement models[J]. Journal of Derivatives, 1995, 3(2):73-84.

Study on Asymmetric Effect of Risk Transmission between Different Financial Sectors in China

ZENG Yu-feng1, JIAN Zhi-hong2, PENG Wei2

(1. School of Economics, Fudan University, Shanghai 200433, China；2. School of Economics HUST, Wuhan 430074, China；3. School of Finance, Zhongnan University of Economics and Law, Wuhan 430073, China)

Ever since the 2008 global financial crisis, the supervision of systemic financial risk has been a hot topic in the field of academic and policy-making departments, both at home and abroad. Especially since 2012, financial system reform began to accelerate, and investment constrain have been gradually deregulated. The extensive relevance and intersectionality of the financial services business brought about significant changes in the financial sector, which led to a substantial increase in systemic financial risk.

The multivariate quantile regression model provides a good tool for analyzing systemic risk. Considering the deficiency of original MVMQ-CAViaR model ignores the asymmetric impacts of positive and negative shock. In this paper, it is extended to asymmetric MVMQ-CAViaR model and joint asymmetric MVMQ-CAViaR model. Subsequently, these models are used to study China's financial industry risk transmission effect between different sectors. Then both Kupiec LR(likelihood ratio) test and dynamic quantile test are used to backtest the prediction performance of these models.

The results show that：Banks have significant spillover effects on securities and insurance sectors, while securities can just unidirectional absorb other sectors' risk；The impacts of good and bad news exhibit leverage effect to some extent to their own as well as other sectors. In general, negative shock has greater effect than positive effect. Furthermore, joint negative impact will amplify the current risk level；Two newly constructed models can significantly improve the risk prediction accuracy, and joint asymmetric MVMQ-CAViaR model is relatively more competitive.

Important practical and social implication are suggested．First of all. Regulators should pay special attention on strengthening the disclosure system of bank risk and the transparency of bank financial information. Then policy makers should strengthen the macro-prudential regulatory requirements and build good co-operation relationship between different industries in order to deal with emergency warning system.

risk transmission；MVMQ-CAViaR model；asymmetric characteristics；systemic risk

1003-207(2017)08-0058-10

10.16381/j.cnki.issn1003-207x.2017.08.007

2016-02-27；

2017-03-07

中央高校基本科研业务费资助项目(2016AD007)；国家自然科学基金资助项目(71402191)

简志宏(1968-)，男(汉族)，四川泸州人，华中科技大学经济学院教授，博士生导师, 研究方向：金融数学、宏观金融,E-ml：jian8822@sina.com.

F830.91

A