三轴向振动台运动耦合装置的参数优化*

刘志华，蔡晨光，于 梅，夏 岩，李京胜

(中国计量科学研究院力学与声学计量科学研究所 北京，100029)

三轴向振动台运动耦合装置的参数优化*

刘志华，蔡晨光，于 梅，夏 岩，李京胜

(中国计量科学研究院力学与声学计量科学研究所 北京，100029)

通过建立三轴向振动台运动耦合装置的传递模型，根据需求频率范围合理选择运动耦合装置刚度。采用有限元方法求解气体润滑问题，仿真分析了供气压力和气膜厚度对气体静压轴承刚度的影响。结果表明，气体静压轴承的刚度随着供气压力的增大而增大，在特定的供气压力下存在一个使气体静压轴承的刚度取得极值的气膜厚度极值点。在此基础上，优化得到一组满足运动耦合装置传递特性要求的供气压力和气膜厚度参数，并通过原理样机进行了验证。实验结果表明，优化得出的运动耦合装置参数满足传递特性要求。

三轴向振动台;运动耦合装置;传递特性;气体静压轴承;参数优化

引 言

随着高灵敏度、宽频率范围等振动传感器的发展以及工业上日益增长的高精度振动测量需求，振动传感器的校准正变得越加重要。目前，国际上振动计量正在向更接近实际测量环境的振动计量体系发展。三轴向振动校准方法的研究是接近实际测量环境振动计量体系研究的基础[1-2]。三轴向振动台是整个校准系统的关键部分，用于产生标准的正弦振动环境，其动态特性直接决定校准的准确度和可靠性。运动耦合装置是三轴向振动台的核心部件，用于实现振动台面沿x,y,z3个方向的独立振动。美国白沙导弹靶场采用球形静压轴承连接激振台和振动台面，保证了两联接件之间的刚度，并允许一定角度的转动，避免各轴向激振台的耦合影响[3]。日本IMV公司发明了一种复合结构装置，通过非接触连接形式的静压轴承传递振动，实现了各轴向振动的解耦[4]。液体静压轴承是一种典型的非接触连接形式，其静压油膜具有很强的承载能力，在多轴向振动台中应用广泛[5-6]。气体静压轴承具有高精度、低摩擦和无污染等优点，在运动耦合装置的应用中具有独特的优势[7]。气体润滑理论奠定于1913年，Harrison在保留气体连续性方程中的密度项、引入等温假设的条件下推导出了可压缩Reynold方程[8]。20世纪80年代以来，随着计算机技术和计算流体力学技术的发展，有限差分法、有限体积法、有限元法和边界元法等计算技术的出现，促进了气体润滑技术的发展[9-11]。三轴向振动台中运动耦合装置的运动激励产生于标准电动台，学者们对标准电动台的动力学模型、结构特性和阻抗特性进行了广泛研究[12-14]。有学者指出，被测对象的负载质量和结构刚度等直接影响标准电动台的动力学特性[15-16]。运动耦合装置中的气体静压轴承也势必会对标准电动台的动力学行为和振动输出能力产生重要影响。为了有效地传递标准电动台的振动激励，有必要对三轴向振动台运动耦合装置的传递特性展开研究。

笔者针对三轴向振动台运动耦合装置，建立运动耦合装置的传递模型，采用有限单元方法求解气体润滑问题的雷诺方程。对运动耦合装置的参数优化方法进行研究，通过应用实例进行详细说明，并进行了实验验证。

1 动力学建模

1.1 系统描述

如图1所示，三轴向振动台由3个标准电动台、运动耦合装置和振动台面组成。其中，3个标准电动台分别沿3条正交轴线方向(x,y,z)布局，形成一套三轴向正交激励系统；运动耦合装置将来自x,y,z3个方向的振动激励合成空间运动轨迹提供给振动台面；被校传感器通过安装适配器固定在振动台面，以获得空间运动轨迹的振动输入。

为实现空间运动轨迹合成要求，运动耦合装置不能与任一方向的标准电动台刚性连接，可采用气体静压轴承的连接形式，结构原理如图2所示。x,y,z轴的气膜能够用于传递相同方向标准电动台的振动，另外又可为垂直方向的运动提供导向功能，但却不会对其运动形成约束。运动单元的x轴方向设置的一个传力导向机构用于振动传递，另一个传力导向机构为随动用于保持刚度，y轴方向也同样设置两个传力导向机构，z轴则仅在底部设置一个传力导向机构。每个传力导向机构是通过内外两个气膜夹住运动单元，从而实现往返方向振动的传递。

1.2 传递模型

三轴向振动台的空间运动轨迹合成基于标准电动台的振动产生和运动耦合装置的振动传递，三轴向振动台单轴向的传递模型如图3所示。可将标准电动台简化成一个两自由度机械系统,其中：m1，k1和c1分别为动圈台面质量、支承弹簧刚度和阻尼；m2，k2和c2分别为线圈质量、与动圈台面的刚度和阻尼。另外，将传力导向机构简化成一个两自由度机械系统，其中：m4为运动单元的质量；运动单元与静压板和动圈台面构成的气体静压轴承的刚度均为k4；c3，c4为阻尼均；k3为动圈台面和静压板之间机械连接的刚度；x1，x2，x3和x4分别为动圈台面、线圈、静压板和运动单元的振动位移；R为线圈电阻；L为线圈电感；I为电路电流；E为输入电压；Ke为反电动势常数；Kf为电磁力常数；Eback为反电动势；FC为励磁线圈的电磁力。

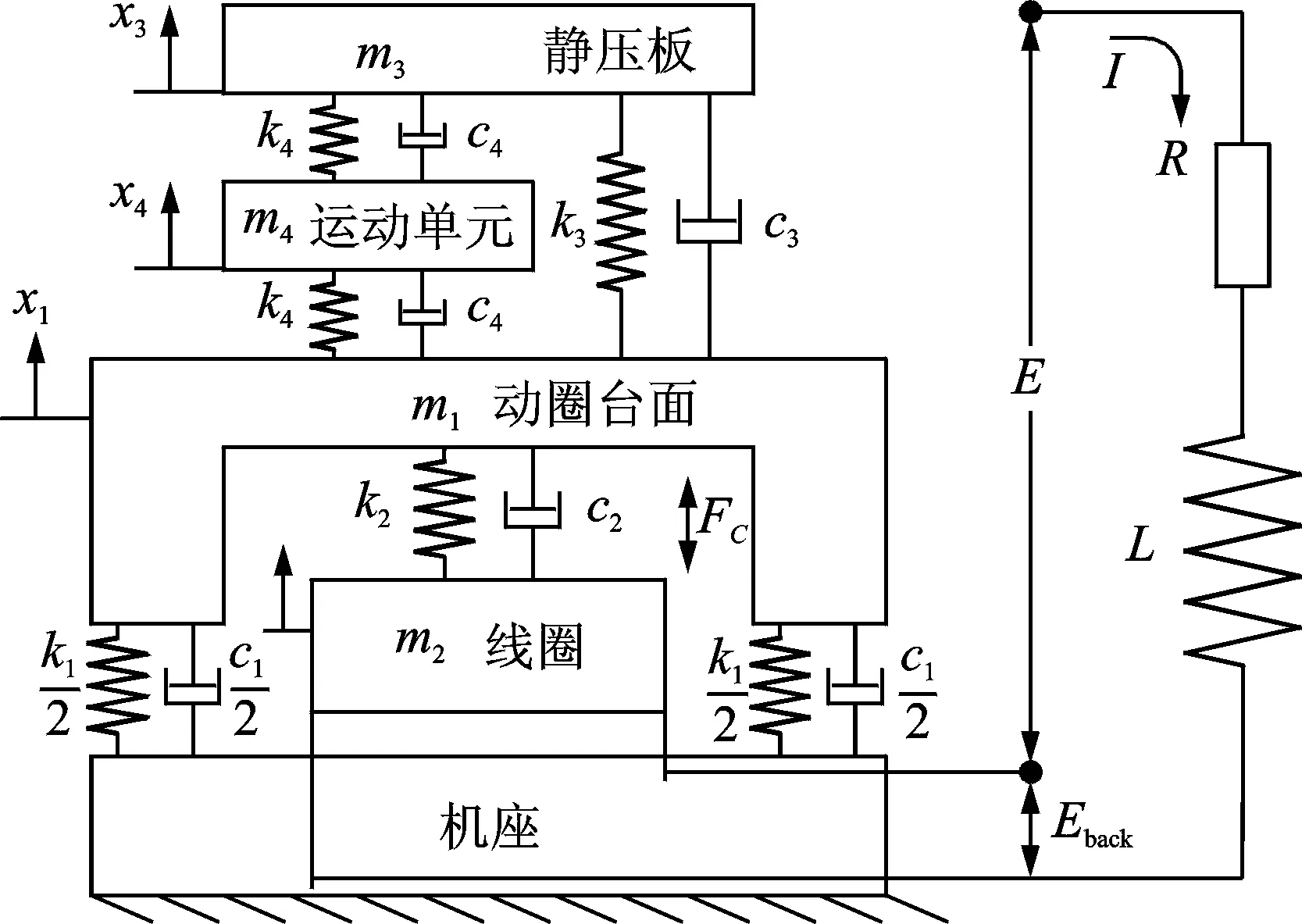
图3 振动台动力学模型Fig.3 Dynamic model of the exciter

根据图3建立三轴向振动台的动力学方程

(1)

该动力学模型中动圈台面和线圈的质量、刚度和阻尼等参数由标准电动台决定。运动单元和静压板的质量以及二者之间的刚度和阻尼取决于运动耦合装置的结构。上述参数的确定方法已较为成熟，在此不做详细介绍。

2 刚度求解

(2)

δj为Kronecker delta函数，即

(3)

其中：0为在无节流孔处；1为在有节流孔处。

(4)

其中：F为n×1维的待求节点压方函数；K为n×n维的刚度矩阵。

K第i行第j列的元素为

(7)

图4 有限单元模型Fig.4 Finite element model

(8)

其中：Ar为节流孔面积；φ为修正系数。

φr根据节流孔处节点压力p的不同，有

(9)

其中

(10)

通过求解式(5)，得到Ω域中各单元体的节点压力大小。在此基础上计算气体静压轴承的承载能力W为

(11)

如果给气膜间隙减小Δh，可求出对应的承载能力W1，则轴承的刚度为

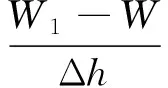
(12)

3 参数优化

3.1 优化问题

三轴向振动台的振动激励产生于3个标准电动台，并通过运动耦合装置进行传递，因此单轴向的振动能力取决于标准电动台的动力学特性和运动耦合装置的传递特性。

根据式(1)计算出图3中四自由度机械系统的前两阶固有频率ω1和ω2。为了保证足够宽的工作频率范围，应该合理设计运动耦合装置中的刚度k3和k4，使ω1和ω2之间的频率范围覆盖运动耦合装置所需要的频率范围，即满足

(13)

通过数值计算搜索出满足频率范围要求的k3和k4组合，具体流程为：a.以k3和k4为坐标轴建立平面搜索区域，并确定k3和k4的搜索范围；b.在搜索范围内选定某一k3和k4组合，通过式(1)计算前两阶固有频率ω1和ω2，若满足式(13)，则认为选定的刚度组合满足传递特性要求；c.采用极坐标或直角坐标方式搜索并确定满足传递特性要求的k3和k4组合的可行区域或边界；d.从可行区域中选择一组k3和k4组合作为运动耦合装置的刚度取值。其中：k3由动圈台面和静压板的机械连接决定，可以通过增大或减小直径来调整刚度；k4取决于运动单元与静压板和动圈台面构成的气体静压轴承。设计加工完成后，节流孔布局和承压面积就已确定，仅能通过供气压力和气膜间隙来调整刚度。

3.2 应用实例

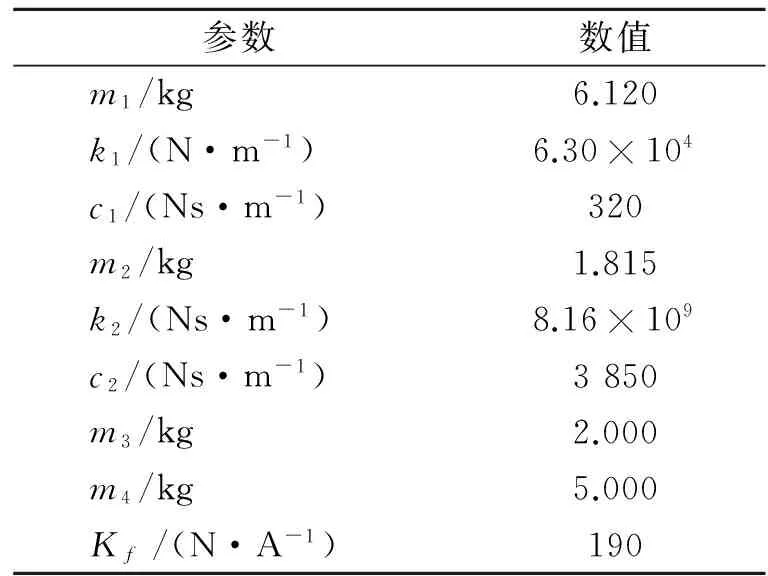
表1 标准电动台参数Tab.1 Parameters of the exciter

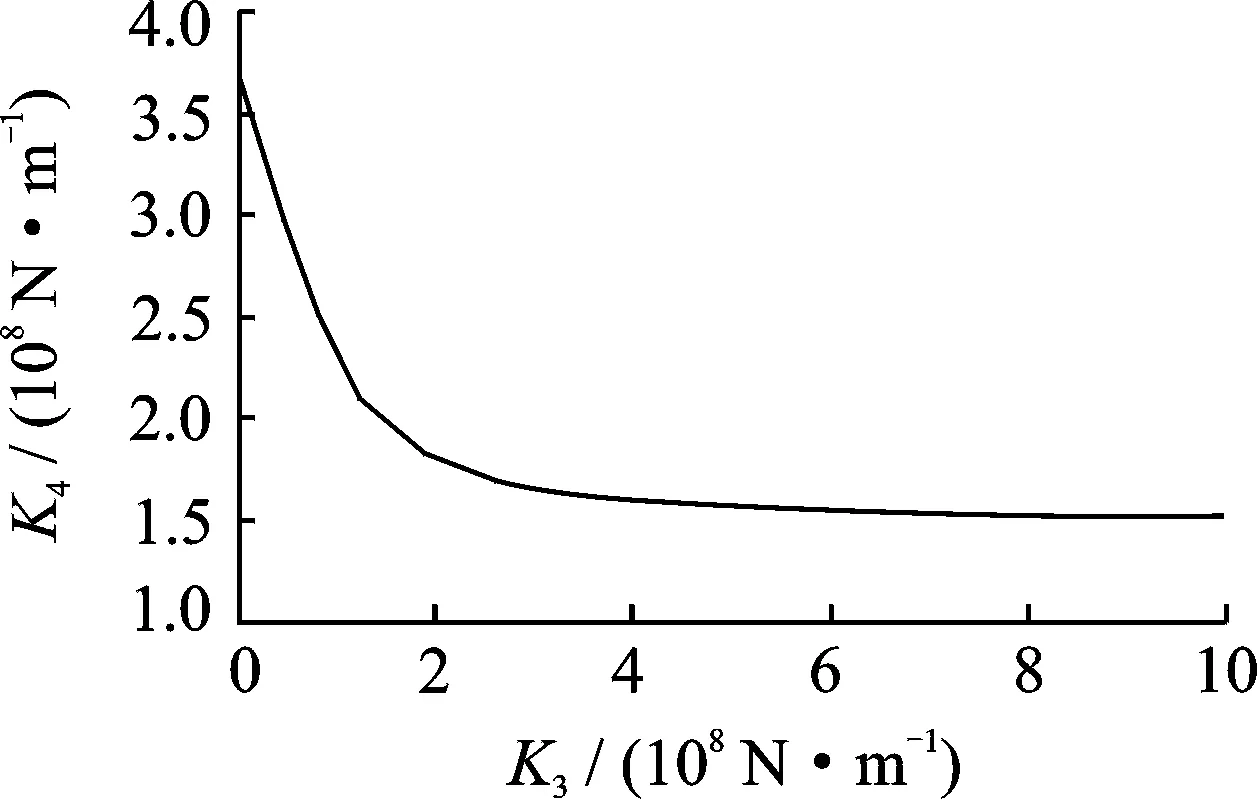
图5 边界刚度曲线Fig.5 The boundary stiffness curve

按照优化结果k3和k4，取c3=5 000 Ns/m和c4=5 000 Ns/m。优化的单轴向加速度-电流幅频特性如图6中的虚线所示，图6中的实线为假设运动耦合装置刚性联接的理想曲线。可以看出：优化曲线的低阶固有频率和理想曲线较为接近，约为10 Hz；高阶固有频率分列成两个谐振频率，其中较低的谐振频率约为1 515 Hz，满足式(13)的优化目标要求。仿真结果表明，选取的刚度组合满足运动耦合装置的幅频特性要求。

图6 优化幅频特性Fig.6 Optimized amplitude frequency response

对供气压力和气膜间隙进行优化，以满足气体静压轴承的刚度要求。气体静压轴承的承压面积和节流孔布局如图7所示，其中节流孔的直径d为0.2 mm。

图7 节流孔布局(单位：mm)Fig.7 Throttle hole layout(unit:mm)

根据式(5)和式(12)求解气体静压轴承的气膜压力和刚度。气体参数ρa=1.23×10-8N·s/cm-4，pa=1×105Pa，η=1.8×10-9N·s/cm-2。当供气压力和气膜间隙为p0=6×105Pa和hm=0.018 mm时，1/4承压面积上的气膜压力分布如图8所示，气膜压力在各节流孔出口最高，并逐渐向四周扩散，在承压边界最小接近大气压。不同供气压力和气膜厚度时，气体静压轴承的刚度如图9所示。在特定的供气压力下，当气膜厚度逐渐增大时，刚度先增大后降低，即存在一个最大值。气体静压轴承最适宜工作在最大值状态下，此时所需要的供气压力最小，且刚度随气膜厚度的变化敏感度最小。另外，刚度随着供气压力增大的增大而增大。当供气压力为6.0×105Pa时，刚度最大值达到1.72×104N/m，满足k3的取值要求，对应的气膜厚度为0.018 mm。可见，根据运动耦合装置的传递特性目标要求，选择合适的运动耦合装置的机械连接刚度和气体静压轴承刚度组合，优化得出的气体静压参数可用于三轴向振动台的设计和调试，如表2所示。

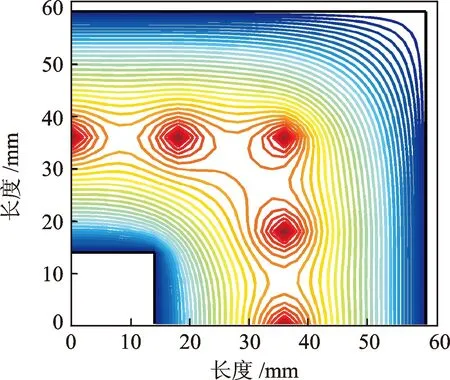
图8 气膜压力分布Fig.8 Gas film pressure distribution

图9 气膜厚度与供气压力对刚度的影响Fig.9 Influence of gas supply pressure and gas film thickness on the stiffness

表2 运动耦合装置的优化参数Tab.2 Optimized parameters of the cross-coupling unit

4 实 验

图10 三轴向振动台实验样机Fig.10 Experimental prototype of the tri-axis vibration exciter

通过三轴向振动台的原理样机来验证运动耦合装置在需求频率范围内的传递特性，原理样机如图10所示。优化目标频率范围为20 Hz～1 000 Hz，由于低频时较容易实现，因此主要验证1 000 Hz时的传递特性。采用优化得出的供气压力和气膜厚度等参数调试原理样机，分别利用1 kHz的标准正弦驱动信号激励各轴向标准电动振动台振动，通过三轴向加速度计测量得出台面振动，如图11所示。

图11 各轴向振动波形Fig.11 Waveform of the axial vibrations

可以看出，测量得出台面沿x,y,z轴向的加速度输出均接近标准正弦信号，正弦信号的幅值比较平稳，相位连续，说明气体静压轴承连接形式的运动耦合装置能够稳定的传递各轴向振动。

z轴向振动的频谱如图12所示。可以看出,振动信号的频率成分明显集中分布在1 kHz，基波的幅值接近12 m/s2，最大的2次谐波幅值约为0.5 m/s2，其余高次谐波幅值很小，因此波形失真度并不大。实验结果表明，原理样机的运动耦合装置能够良好地传递1 000 Hz的高频振动，说明优化得出的供气压力和气膜厚度参数满足运动耦合装置需求频率范围内的传递特性。

图12 z轴向振动频谱Fig.12 Frequency spectrum of the z-axial vibration

5 结束语

采用有限单元方法求解气体润滑问题的雷诺方程，分析供气压力和气膜厚度对气体静压轴承刚度的影响。提出运动耦合装置的参数优化方法，优化得到一组满足运动耦合装置传递特性要求的供气压力和气膜厚度参数。实验结果表明，优化得出的运动耦合装置参数满足传递特性要求。

[1] Umeda A,Onoe M,Sakata K,et al.Calibration of three-axis accelerometers using a three-dimensional vibration generator and three laser interferometers[J].Sensors and Actuators A:Physical,2004,114(1):93-101.

[2] Hof C,Kobusch M.Comparison of the calibration of a heavy multi-component vibration transducer on different exciter systems (calibration of heavy triax-transducer)[C]∥IMEKO 20thTC3,3rdTC 16 and 1stTC22 International Conference Cultivating Metrological Knowledge.Merida,Mexica:[s.n.],2007:9-10.

[3] Edgington F M.A three directional vibration system[J].The Shock and Vibration Bulletin,1986,8:521-527.

[4] Aoki H,Tsutsumi S,Fukushima T,et al.Vibration testing apparatus with increased rigidity in static pressure bearing:U.S.,5549005[P].1996-08-27.

[5] Whiteman W E,Berman M S.Fatigue failure results for multi-axial versus uniaxial stress screen vibration testing[J].Shock and Vibration,2002,9:319-328.

[6] Harman C,Pickel M B.Multi-axis vibration reduces test time[J].Evaluation Engineering,2006,45(6):44-47.

[7] 刘暾,刘育华,陈世杰.静压气体润滑[M].哈尔滨：哈尔滨工业大学出版社,1990：122-153.

[8] Bulat M P，Bulat P V.The history of the gas bearings theory development[J].World Applied Sciences Journal，2013,27(7):893-897.

[9] Reddi M M.Finite element solution of the incompressible lubrication problem[J].Transcations of ASME,Series F,1969,91(3):254-533.

[10]Pandian M C.A new method for the numerical solution of the Reynolds equation for gas-lubrication slider bearings[J].Journal of Engineering Mathematics,1985,19(3):3-19.

[11]Shooroki H R,Meybodi R R,Karbassi S M,et al.Numerical solution of Reynold′s equation governing noncircular gas bearing system using radial basis function[J].Iranian Journal of Science and Technology,2014,38(A4):389-397.

[12]McConnell K G.Vibration testing:theory and practice[M].New York:John Wiley &Sons,1995:419-460.

[13]Lang G F.Understanding the physics of electrodynamic shaker performance[J].Sound and Vibration,2001,35(10):24-33.

[14]Hirunyapruk C，Plangsangmas V.Investigation into the resonances of vibration exciter[C]∥ IMEKO 22ndTC3,12thTC5 and 3rdTC22 International Conferences.Cape Town:[s.n.],2014:1-4.

[15]Varoto P S,de Oliveira L P R.Interaction between a vibration exciter and the structure under test[J].Sound and Vibration,2002,36(10):20-26.

[16]Delima W J,Ambrose M N.Experimental characterization and simulation of vibration environmental test[J].Topics in Modal Analysis,2015,10:45-55.

10.16450/j.cnki.issn.1004-6801.2017.04.022

* 国家自然科学基金青年基金资助项目(51605461)；中国博士后科学基金资助项目(2016M591229)；质检公益性行业科研专项资助项目(201410009)

2016-03-12；

2016-04-06

TH39

刘志华，男，1987年10月生，博士后。主要研究方向为振动计量技术和方法。曾发表《Research on the dynamic coupling of the rigid-flexible manipulator》(《Robotics and Computer Integrated Manufacturing》2015，Vol.32)等论文。 E-mail:liuzhihua@nim.ac.cn