力控法兰的模糊PID恒力控制方法*

黄 婷，孙立宁，王振华，禹鑫燚，陈国栋

(1．苏州大学机器人与微系统研究中心 苏州，215021)(2.浙江工业大学信息工程学院 杭州，310023)

力控法兰的模糊PID恒力控制方法*

黄 婷1，孙立宁1，王振华1，禹鑫燚2，陈国栋1

(1．苏州大学机器人与微系统研究中心 苏州，215021)(2.浙江工业大学信息工程学院 杭州，310023)

针对工业机器人进行接触式作业过程中对末端接触力的要求，提出了一种基于力控法兰的末端恒力控制方法。对力控法兰进行了分析建模与参数辨识，设计了模糊控制与比例积分微分(proportion integral derivative,简称PID)控制并行的模糊PID控制器，通过Matlab仿真对纯模糊控制与模糊PID控制效果进行了对比，并研究了模糊PID控制器各参数对控制性能的影响。最后，搭建了基于Labview和外部设备互连(peripheral component interconnect,简称PCI)总线数据采集卡的实验平台，对力控法兰末端输出力进行了实验验证。仿真结果表明，纯模糊控制可提高系统响应性能，但存在一定的稳态误差。加入PID控制与模糊控制并行控制后，仿真与实验证明，阶跃响应的稳态误差消除，正弦跟随效果明显改善，恒力控制输出力在期望力F=10 N时波动误差为±0.8 N。因此，通过模糊PID控制可实现力控法兰末端的恒力控制，具有较好的动态响应性和跟随鲁棒性。

力控法兰；恒力控制；实验测定法；模糊PID控制

引 言

随着工业机器人的快速发展，其在各工业领域的应用越来越广泛[1]。一些接触式作业场合，要求工业机器人具有对接触力的感知与控制能力，以达到精密操作的要求，例如，磨削、抛光和装配作业等[2-3]。在进行磨抛作业时，加工工具随着使用而发生磨损，产生表面位置误差[4]，使接触力发生变化，进而影响加工效果。因此，实现工具与工件的恒力接触对工业机器人在接触式作业中的应用有着重要的实践意义。

目前，实现接触力控制的方式主要有主动力控制和被动力控制两种[5]。主动力控制由机器人控制器实现，一般采用力/位混合控制的方法[6-8]。由于该方法需要同时实现力和位置的控制，存在力/位耦合，因而实现较为复杂。相比较而言，被动力控制引入独立于机器人的柔性装置，将力控制从机器人控制器分离出来，通过柔性装置实现，比主动力控制简单易行，因此在工业应用场合有更广泛的应用前景。文献[9]提出了远中心柔顺手腕(remote center compliance,简称RCC)用于装配作业,能对任意柔顺中心进行顺从运动。由于RCC装置的柔顺中心一旦确定，就很难调整，因而通用性较差。文献[10]给机器人研磨和抛光系统的研抛砂带增加了柔顺机构，在接触后能够自适应改变研磨接触力,代替了人工研磨涡轮机叶片。文献[11]基于气囊抛光加工技术分析了下压深度和充气压力对接触力的影响，采用BP神经网络PID控制策略进行抛光接触力控制，获得了较好的加工效果。

笔者在以上研究的基础上，引入一种力控法兰装置。该装置可被动上下调节以适应机器人和工件之间的距离，伺服阀根据控制信号对气缸内的气压进行调节，使位移被动发生变化的过程中接触力保持恒定，从而实现末端恒力控制。对力控法兰进行建模，设计一种模糊PID控制器，以改善其末端输出力的动态性能和鲁棒性。

1 力控法兰建模

力控法兰装置模型图和样机如图1所示，该装置主要包括法兰接口、上基座、导向机构、下基座、伺服阀、气缸以及位移传感器。其工作原理如下：首先，给伺服阀预设一个气压值，使气缸对基座和机械接口产生一定张力。导向机构约束上下基座只能在一个方向相对移动，当工具与工件接触产生接触力，使得上下两端压缩，压力传感器反馈气缸腔内气压值。当接触力偏小时，伺服阀进气口打开向气缸腔内进气以增加压力；当接触力偏大，气缸腔内的气压超过设定气压时，伺服阀排气口打开，通过气管向外排气以减小压力。在平衡状态下，依靠伺服阀维持气缸腔内的压力保持不变，从而使输出力保持恒定。根据装置结构，综合考虑伺服阀流量方程、气缸质量流量连续性方程及系统的力平衡方程，对力控法兰进行分析与建模。

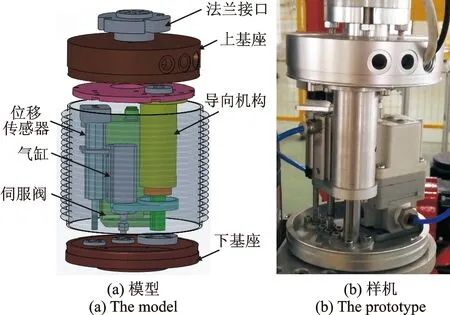
图1 力控法兰装置Fig.1 Force-controlled flange device

1.1 力控法兰流量模型

力控法兰气体流通原理图如图2所示。法兰的输入信号为控制电压u，输出为力Fn。根据输入的控制电压u，控制伺服阀输出气压至低摩擦气缸。伺服阀和气缸之间采用气管连接(图2中虚线表示气管连接)，气压作用于气缸，产生输出力Fn。

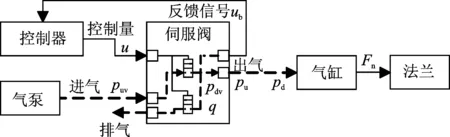
图2 力控法兰气体流通原理图Fig.2 Schematic diagram of gas flow in force-controlled flange

伺服阀供气口通过的流量与供气口压强、出气口压强和阀口开度有关。采用Sanvile流量公式有

(1)

其中：q为通过阀口的流量；Puv为供气口的压强；Pdv为出气口的压强；Av为阀口的有效面积；k为绝热系数；Cf为伺服阀节流口流量参数；T为绝对温度；Rc为理想气体常数。

在实际抛磨中，一般所需接触力较小，故出气口气压通常较小，式(1)中的第1式成立。此时，假设供气口压强和伺服阀内气体温度一定，则阀口流量仅与阀口有效面积有关，而阀口有效面积与伺服阀控制电压有关，其影响的是出气口的压强，因此可以认为流量公式是与控制电压u及阀出气口压强Pdv有关的函数。将其在零位附近线性化，得到伺服阀的流量增量模型为

Δq=K1Δu+K2ΔPdv

(2)

伺服阀输出的气流经过一段长度为L的气管，进入气缸的上腔。气管中气体流量等于伺服阀出口流量。根据Anderson理论，有

q=K3(Pu-Pd)

(3)

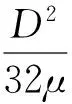
根据式(3)得到气管内气体流量增量模型

Δq=K3(ΔPu-ΔPd)

(4)

气体经过伺服阀和气管进入气缸。假设气缸内的气体为理想气体，满足理想气体状态方程，则有

Pd=ρdRcTd

(5)

其中：Pd为气缸腔内的气体压强；ρd为腔内气体密度；Td为腔内气体的热力学温度。

假设气体流通过程中温度满足绝热过程，根据质量流量q等于该腔内气体质量m的变化率。结合式(5)推导可得气缸腔内流量模型为

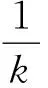
(6)

分别将式(2)，(4)和(6)进行Laplace变换，有

Q(s)=K1U(s)+K2Pdv(s)

(7)

Q(s)=K3Pu(s)-K3Pd(s)

(8)

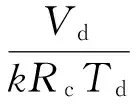
(9)

气管进气口压强Pu即伺服阀出气口压强Pdv，即Pdv(s)=Pu(s)。联立式(7)～(9)可得

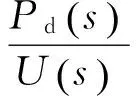
(10)

因此，根据对力控法兰各部分的流量进行建模分析，得到装置从输入的伺服阀控制电压到气缸内输出压强的关系模型，如式(10)所示。

1.2 力控法兰力平衡方程

腔内压强Pd作用于气缸，气缸受力面积为Ad。对力控法兰进行受力分析，如图3所示。

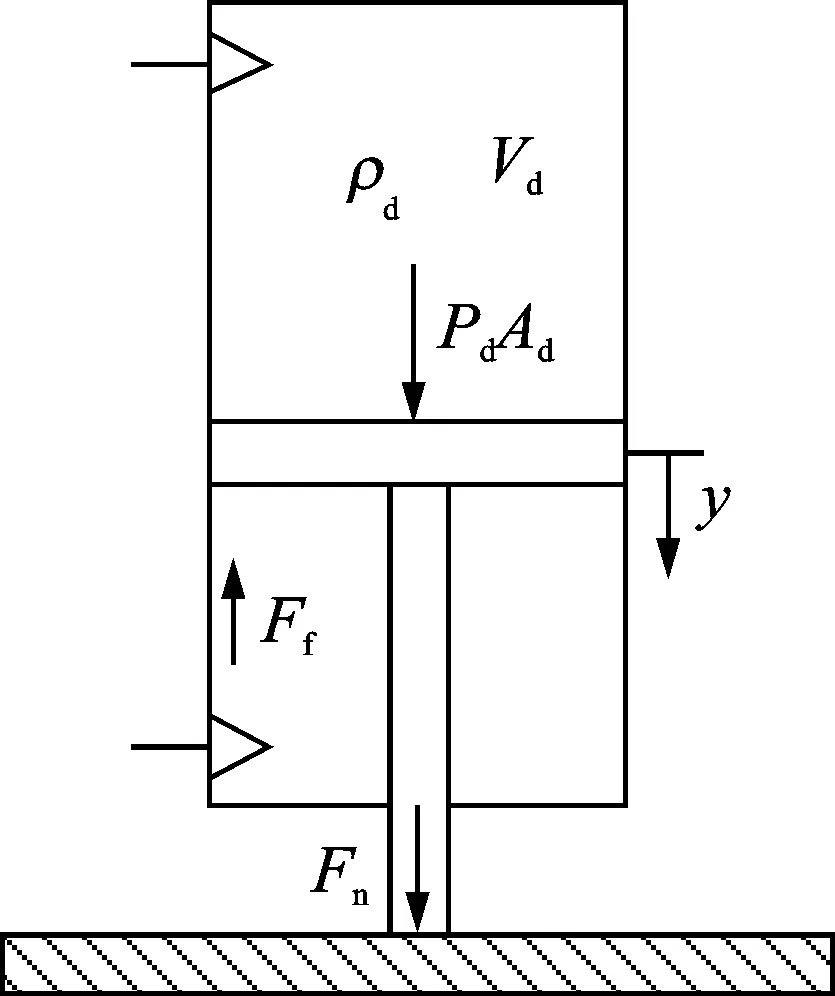
图3 力控法兰受力分析Fig.3 Force analysis of force-controlled flange

根据牛顿第二定律，有

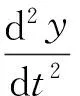
(11)

其中：Fn为力控法兰输出力；Ff为摩擦力；M为气缸连接部件的总质量；Cp为黏性阻尼系数；y为气缸活塞运动的位移。

忽略低摩擦气缸的摩擦力，对式(11)进行拉普拉斯变换，有

(12)

末端工具与工件接触，作用力Fn使力控法兰被动产生位移y。等效刚度系数为Ke，则有

Fn(s)=KeY(s)

(13)

联立式(12)和(13)可得

（一）在主推品种方面 武隆县在肉牛产业发展中，主推西门塔尔牛和安格斯牛，首先用西门塔尔牛冷冻精液配种川南山地黄牛经产母牛，再用安格斯牛冻精配种“西杂牛”，并将“红西本”三杂牛作为商品牛进行育肥出售。

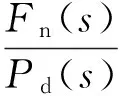
(14)

综合式(10)，式(12)～(14)，装置的传递函数框图如图4所示。

图4 力控法兰开环系统传递函数框图Fig.4 Open-loop system transfer function diagram of force-controlled flange

结合式(10)与式(14)，系统的开环传递函数可表示为

G(s)=

(15)

得到力控法兰的输入控制量与输出抛磨力之间的模型如式(15)所示。可见，该系统是一个三阶系统。由于该模型中存在许多非线性影响因素，无法对其进行准确量化。为了对系统进行控制，可以将其作为一个“黑盒子”进行参数辨识。

2 力控法兰模型测定

数学模型实验测定是通过给系统施加特定的信号，采集响应输出信号随时间变化的曲线进行分析，从而实现对模型参数的辨识。主要方法有时域测定法、频域测定法和统计相关测定法。笔者采用相对简单易行的时域测定法。为了提高实验测定模型的精度，采用有延迟的n阶惯性环节进行拟合。表达式为

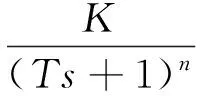
(16)

在t=0时，施加阶跃输入控制电压u，力控法兰输出力F随时间变化的响应曲线如图5所示。

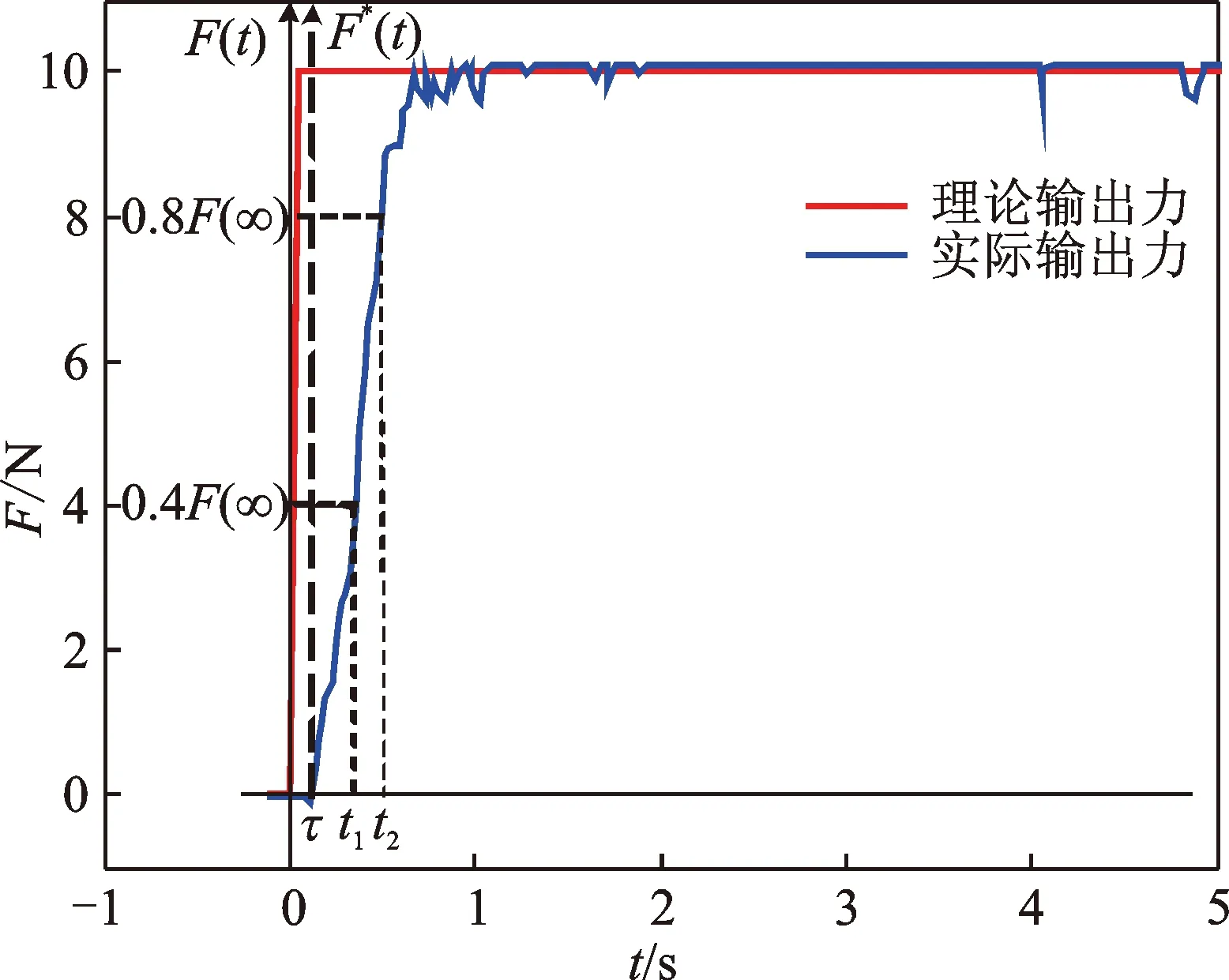
图5 有延迟的n阶拟合两点法Fig.5 N order fitting two-point method with delay

2.1 参数确定

2.1.1 增益K

如图5所示，设给定阶跃输入幅值为u，其增益K可按下式求取

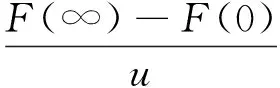
(17)

将u=0.759 2 V,F(0)=0,F(∞)=10.11N代入式(17)，得到K=13.316 6。

2.1.2 延迟时间τ

响应曲线延迟时间τ根据阶跃响应曲线开始出现变化的时刻来确定。如图5所示，在t=0时施加输入信号，t=0.078 s时输出信号响应曲线开始发生变化，因此τ=0.078 s。

2.1.3 阶次n和时间常数T

计算阶次n的近似公式为

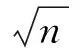
(18)

将计算结果取整，得到阶次n=5。

时间常数为

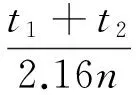
(19)

代入参数，计算得到T=0.059 4 s。

因此，实验测定力控法兰模型为

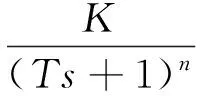
(20)

2.2 模型简化

由于时间常数T=0.059 4 s，分母部分展开后其高阶部分系数远小于1，对系统影响较小，可近似忽略。因此，忽略系统的高阶项，得到模型为

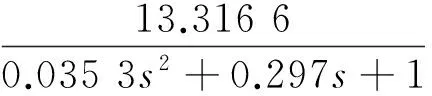
(21)

由拉氏变换延迟定理可知，延迟环节的传递函数可表示为

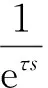
(22)

将eτs按泰勒级数展开，得到

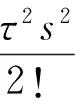
(23)

由于τ很小，忽略高阶项，取其前两项，eτs=1+τs，于是有

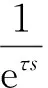
(24)

式(24)表明，在延迟时间很小的情况下，延迟环节可用一个小惯性环节来代替。

得到力控法兰的最终实验测定模型为

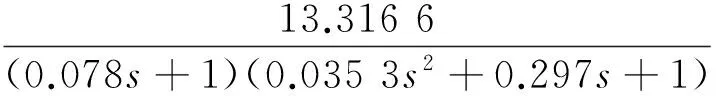
(25)

通过Matlab/Simulink仿真，在t=0时施加一个阶跃输入信号u=0.579 2，所得阶跃响应曲线如图6所示，并与力控法兰实际响应曲线对比进行模型验证。

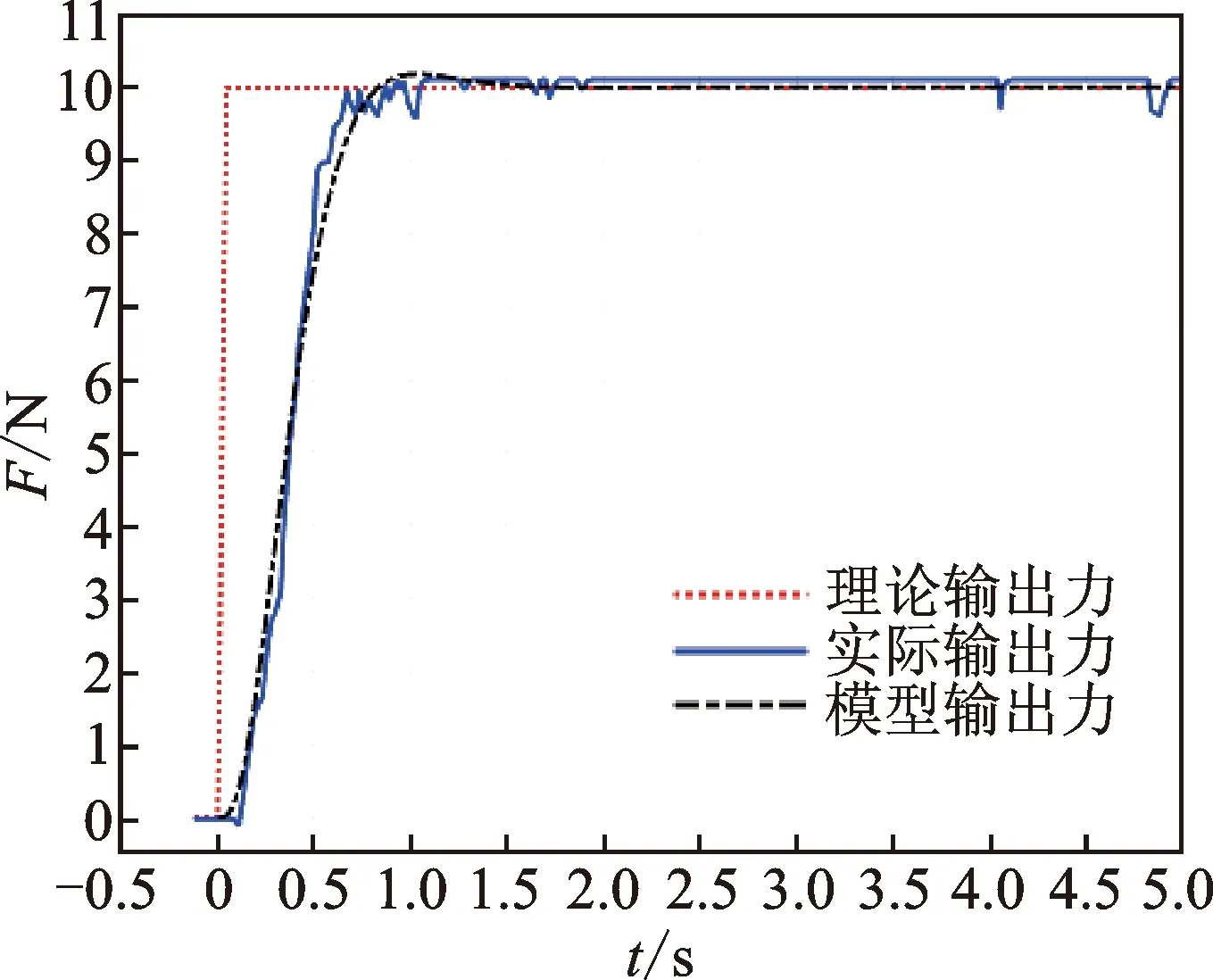
图6 模型验证Fig.6 Model verification

从图6可以看出，模型输出力响应曲线与实际输出力响应曲线总体来说比较接近，说明该模型较好地还原实际模型。但由于实验模型在测定过程中忽略了其高阶项，且实际响应曲线的获取受很多未知因素的影响，数据在一定范围内具有不确定性，因此其上升曲线与实际响应稍有差异。通过对比式(15)理论模型与式(25)实验测定模型可知，两者均为无零点的三阶传递函数，从而验证了理论建模的正确性。因此，实验测定模型可认为是力控法兰系统的近似数学模型。力控法兰被施加阶跃输入信号后，输出力基本无超调，说明系统的稳定性良好。由于三阶系统存在多个惯性环节，使得实际输出响应存在一定的滞后。为了满足工业应用上对系统快速性的要求，需要在此基础上对力控法兰控制系统的快速响应性能进行改善。

3 控制器设计

3.1 控制框架

力控法兰装置的控制原理如图7所示。图中：F0为期望力(设定值)；u为控制器输出给伺服阀的控制信号；P为伺服阀输出到气缸腔内气体形成的气压；Fn为气缸腔内气压向下产生的压力，即力控法兰输出力；Pb为压力传感器检测反馈的气缸腔内气压；Fb为根据压力传感器反馈气压值换算所得，经过标定Fb可准确反馈力控法兰输出力Fn，理论上控制系统稳定后，该值等于设定值F0，从而实现末端接触力的恒力控制；Xb为位移传感器测出的力反馈装置的柔顺变形位移量，可以用来检测感知力控法兰的状态。

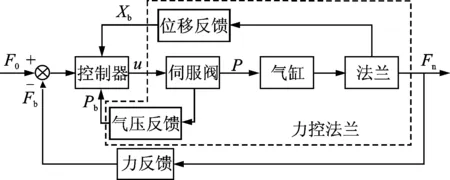
图7 力控法兰控制系统原理图Fig.7 Control system schematic diagram of force-controlled flange

力控法兰的输出力控制具体实现过程如下：在装置启动前给定目标接触力F0，控制器根据控制算法得出应该分配给伺服阀的控制信号u，伺服阀根据控制信号u向气缸输出相应的气压P，并将实际的气压值反馈给控制器，从而得到反馈力Fb。Fb与设定值F0比较，根据所得误差进行下一步的调节，最终使Fb在控制精度范围内等于F0，从而实现对法兰输出力的控制。可以看出，在此过程中，控制器的控制性能直接影响输出力的动态特性和稳定性。

3.2 控制器设计

传统的PID控制方法控制简单且具有良好的稳态精度，然而在系统的抗干扰性及对系统参数时变的鲁棒性都不够理想。力控法兰在运行的过程中具有许多的非线性因素(如气缸摩擦力、被动柔顺产生的位移变化，以及与工件接触的等效刚度等)，因此，实验测定的数学模型只能作为对力控法兰进行控制的近似模型。模糊控制是基于模糊推理和模仿人的思维的方法，不需要精确的系统数学模型，具有较强的鲁棒性，但是单独控制时会产生一定的稳态误差。笔者结合PID控制器与模糊控制器的优点，对力控法兰系统进行控制优化，根据设定的输入信号和反馈信号，计算误差e以及当前误差变化率ec，通过模糊规则进行模糊推理，同时通过PID控制进行调节，将两个控制器的控制量合并输出，从而实现力控法兰的末端输出信号的控制。控制系统框图如图8所示。

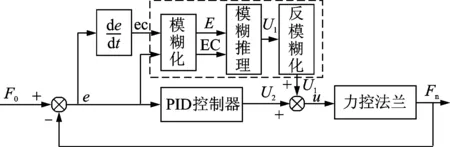
图8 模糊PID控制框图Fig.8 Fuzzy PID control block diagram

图8中，F0为期望力(设定值)，Fn为力控法兰的输出。模糊控制器以误差e和误差变化率ec作为输入，控制量u1作为输出，与PID控制器输出的控制量u2合并为系统的控制量u，实现对力控法兰的末端输出力Fn的控制，使之快速达到设定值并保持稳定。

模糊控制器设计流程如图9所示。主要有4个步骤：a.对系统输入输出进行模糊化处理；b.模糊控制规则提取；c.模糊推理和决策表生成；d.输出的反模糊化处理。

图9 模糊PID控制器设计流程图Fig.9 Flow chart of fuzzy PID controller design

对系统的输入e和ec以及输出u1均采用7段模糊子集{负大，负中，负小，零，正小，正中，正大}描述，记为{NB,NM,NS,ZO,PS,PM,PB}。论域设定为[-6,6]。考虑到对论域的覆盖程度和灵敏度，各模糊子集均选用三角形隶属函数。

控制器设计的原则是通过控制器输出的控制量使系统快速地达到设定目标值并保持稳定。模糊规则的选取直接影响到系统控制的动态性能和稳态性能。

1) 当e较大，此时无论ec为何值，控制量均应该增加以消除误差。

2) 当e较小或等于0，此时为了防止超调过大并使系统快速稳定，需要根据ec来确定控制量的变化。如果ec为正，则说明误差有增大的趋势，应该加大控制量，以抑制误差增大；如果ec为负，则说明误差在减小，此时控制量可取较小值。

根据上述原则，建立模糊控制规则，如表1所示。

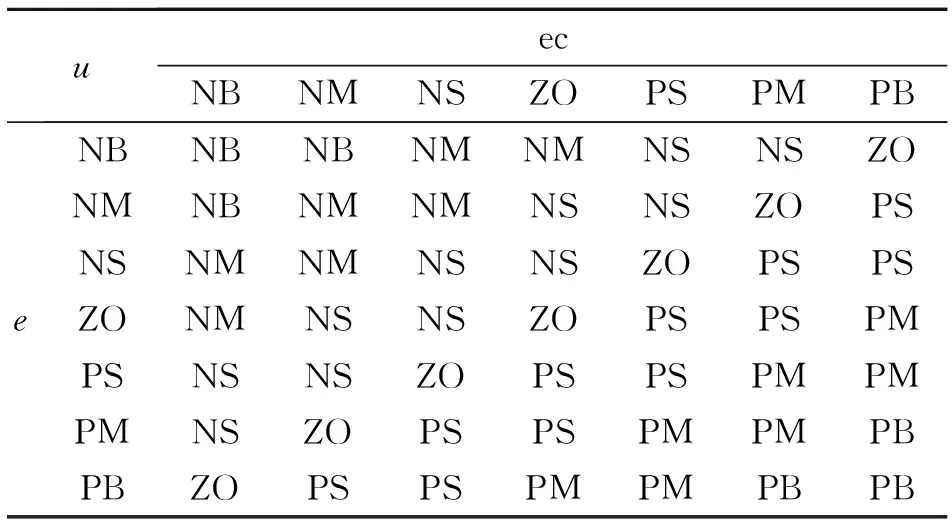
表1 模糊控制规则表Tab.1 Fuzzy control rule table

建立模糊规则后，应用模糊推理得到输出模糊量U1，再反模糊化得到实际控制量u1。由于模糊控制最终会存在一定的稳态误差，PID控制器的积分作用可以消除稳态误差，实现对设定值的无静差跟踪。因此，采用经典PID控制器对模糊控制器进行改进，由PID控制器输出控制量u2，与模糊控制器输出的控制量u1合并为总控制量u，对力控法兰进行控制。

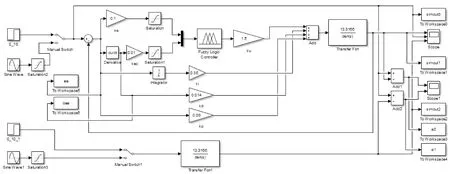
图10 力控法兰模糊PID控制Simulink模型Fig.10 Fuzzy PID control simulink model of force-controlled flange

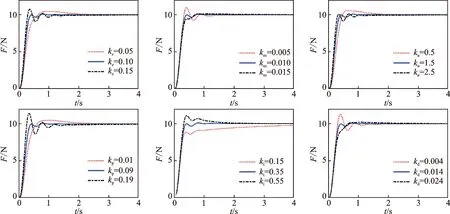
图11 参数ke,kec,ku,kp,ki,kd对阶跃响应的影响Fig.11 Parameters ke,kec,ku,kp,ki,kd effect on step response

4 仿真与实验验证

4.1 仿真验证

为了验证模糊PID控制器对力控法兰动态性能的影响，采用Simulink工具进行仿真。搭建仿真模型如图10所示，模型包括阶跃输入、模糊控制器、PID控制模块、控制对象及系统输出。其中模糊控制器为使用Simulink中的模糊控制工具箱建立的Mamdani模糊控制器，PID模块的比例、积分和微分输出的控制量直接与模糊控制输出的控制量合并为力控法兰模型的控制输入。

模糊规则确定后，模糊控制部分可调节的参数有ke，kec，ku。其中:ke，kec为输入误差和误差变化率的量化因子；ku为输出控制信号的量化因子。分别对模糊控制参数及PID控制参数kp，ki，kd进行调节。各参数取值对响应曲线的影响如图11所示。

从图11可以看出，ke和kp对系统的调节时间影响明显。ke，kp越大，响应越迅速，但参数增大，提高响应时间的同时也引起系统的振荡和超调。kec，kd对系统的超调有抑制作用，但是会使系统稳定的时间变长。ku作为输出控制量的量化因子，对系统的输出有很直观的作用，而积分系数ki对系统趋于稳态值的速度影响显著。积分环节消除稳态误差的作用在图12可进一步明确。

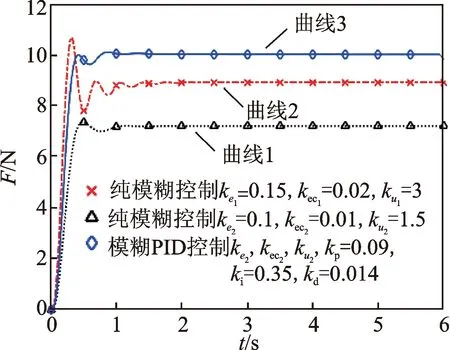
图12 响应曲线对比Fig.12 Response curve comparison

图12中，曲线1和曲线2均存在一定的稳态误差。对比曲线1和曲线2可知，采用单纯模糊控制时，量化因子取值不同，系统最终产生的稳态误差不一样。在曲线1的基础上增加PID控制，系统阶跃响应如曲线3所示。ki消除了曲线1的稳态误差，使系统稳定在设定目标值。另外，由于PID参数中的kp作用与ke相似，kd作用与kec相似，因此，得到某一较理想响应曲线的控制参数可能并不唯一。

为了验证模糊PID控制器的控制效果，分别在对模型进行阶跃响应仿真和正弦跟随仿真。在t=0时输入信号F0=10 N，得到仿真阶跃响应曲线如图13(a)所示。从仿真结果可以看出，未加模糊PID控制的实验测定模型的阶跃响应时间为0.69 s，并存在1.7%的超调量，加模糊PID控制后，系统仿真的阶跃响应时间缩短为0.34 s，经过两次很小的振荡后系统进入稳定状态，基本不存在超调，系统的动态性能和稳态精度都得到了提高。采用频率为0.5 Hz、幅值为10 N的正弦信号作为给定输入信号。系统跟随响应曲线如图13(b)所示。可以看出，加模糊PID控制器后，系统的动态调节速度明显提高，系统响应的滞后明显改善；但由于频率变化太快，系统的幅值削弱较明显。

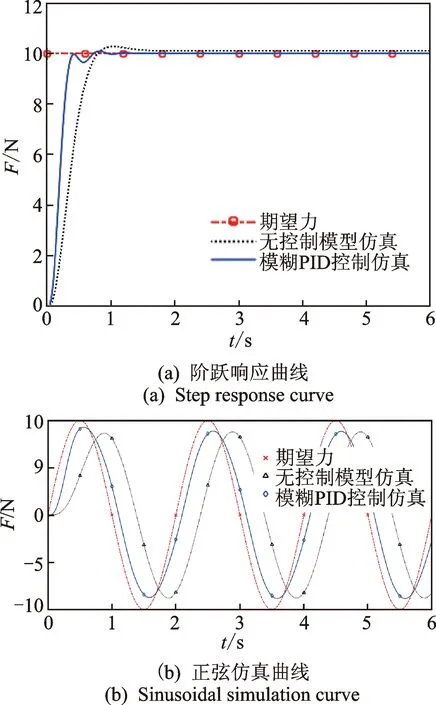
图13 加模糊PID控制前后仿真对比Fig.13 Simulation comparison before and after fuzzy PID control

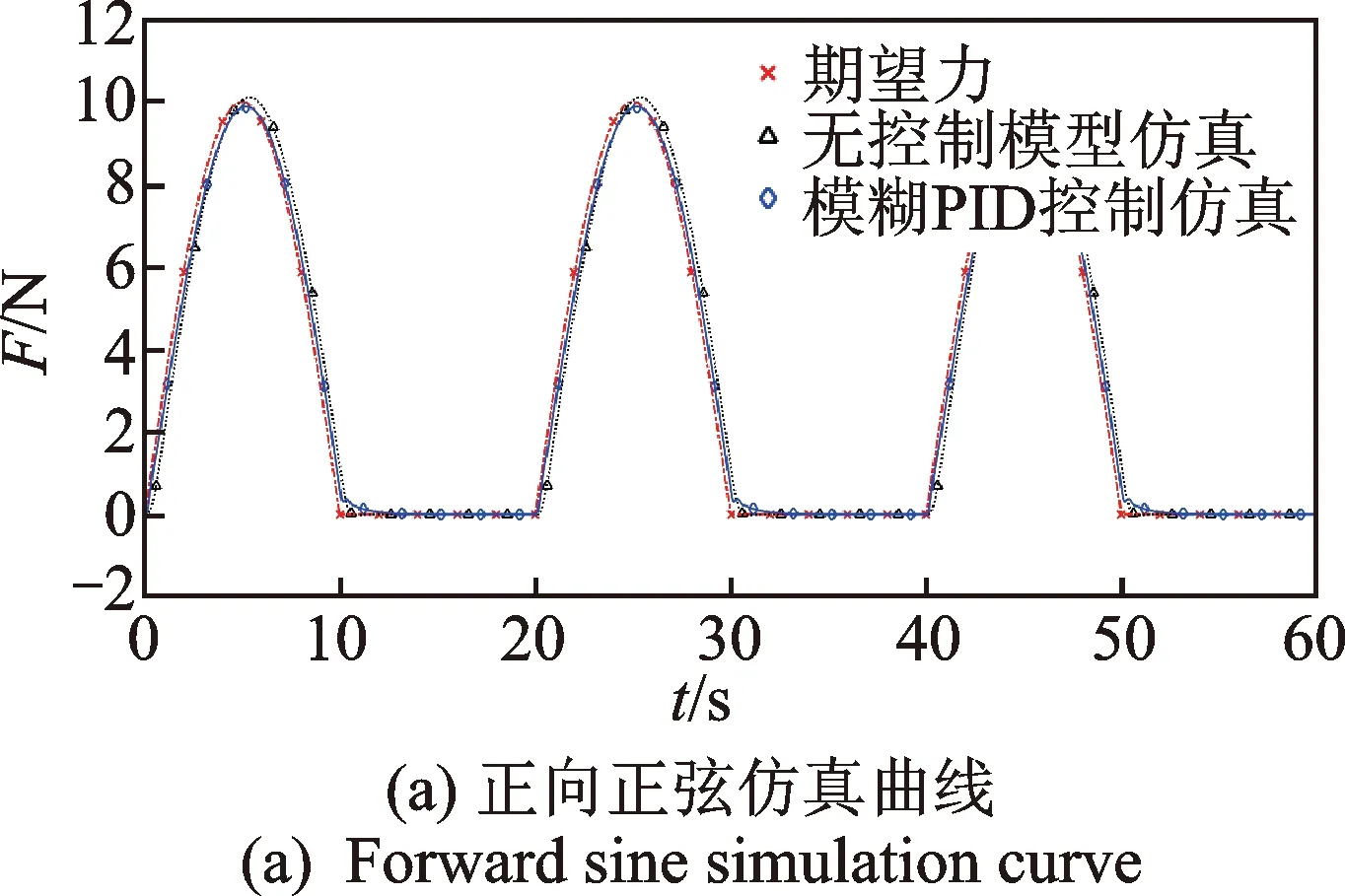
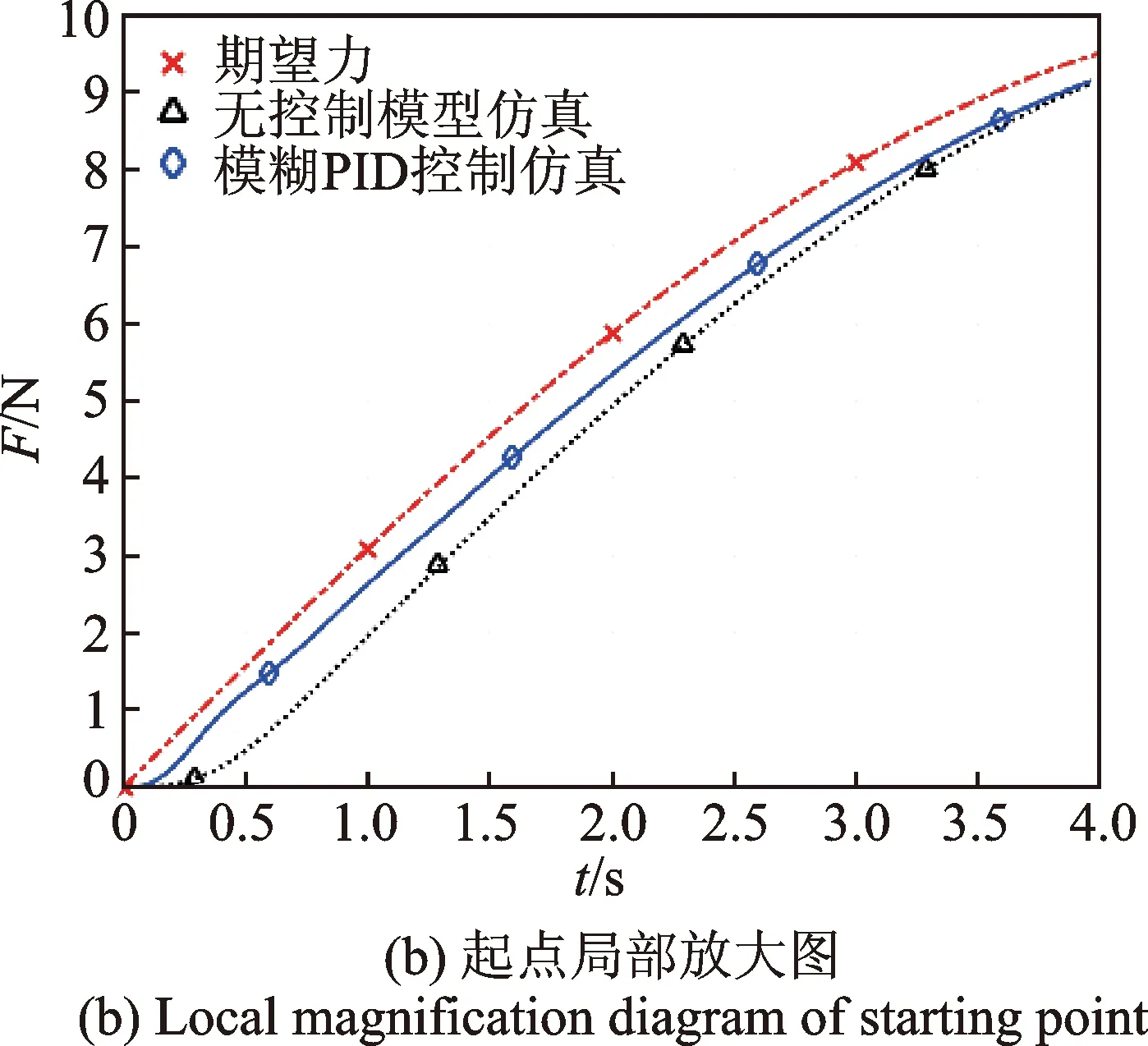
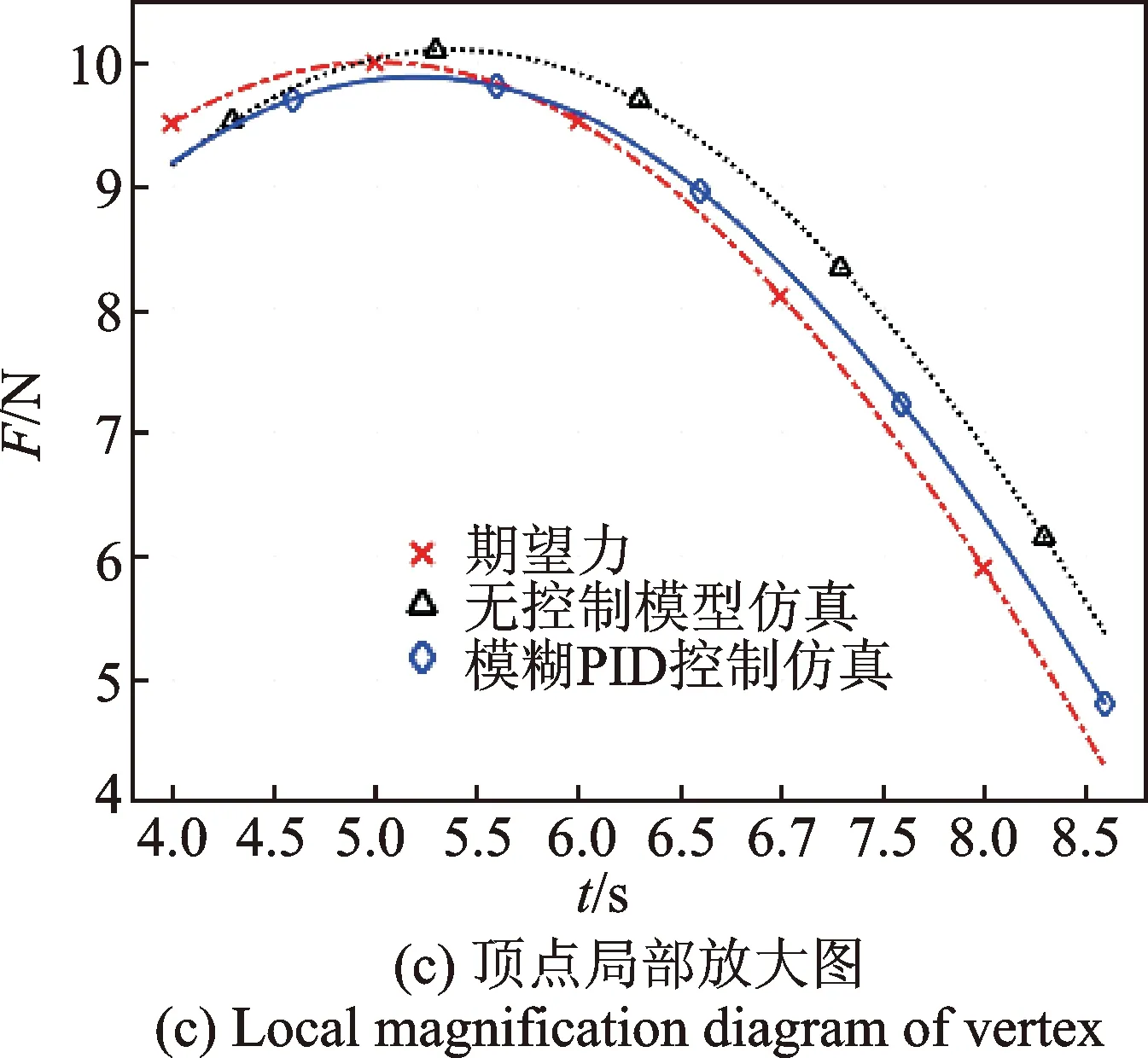
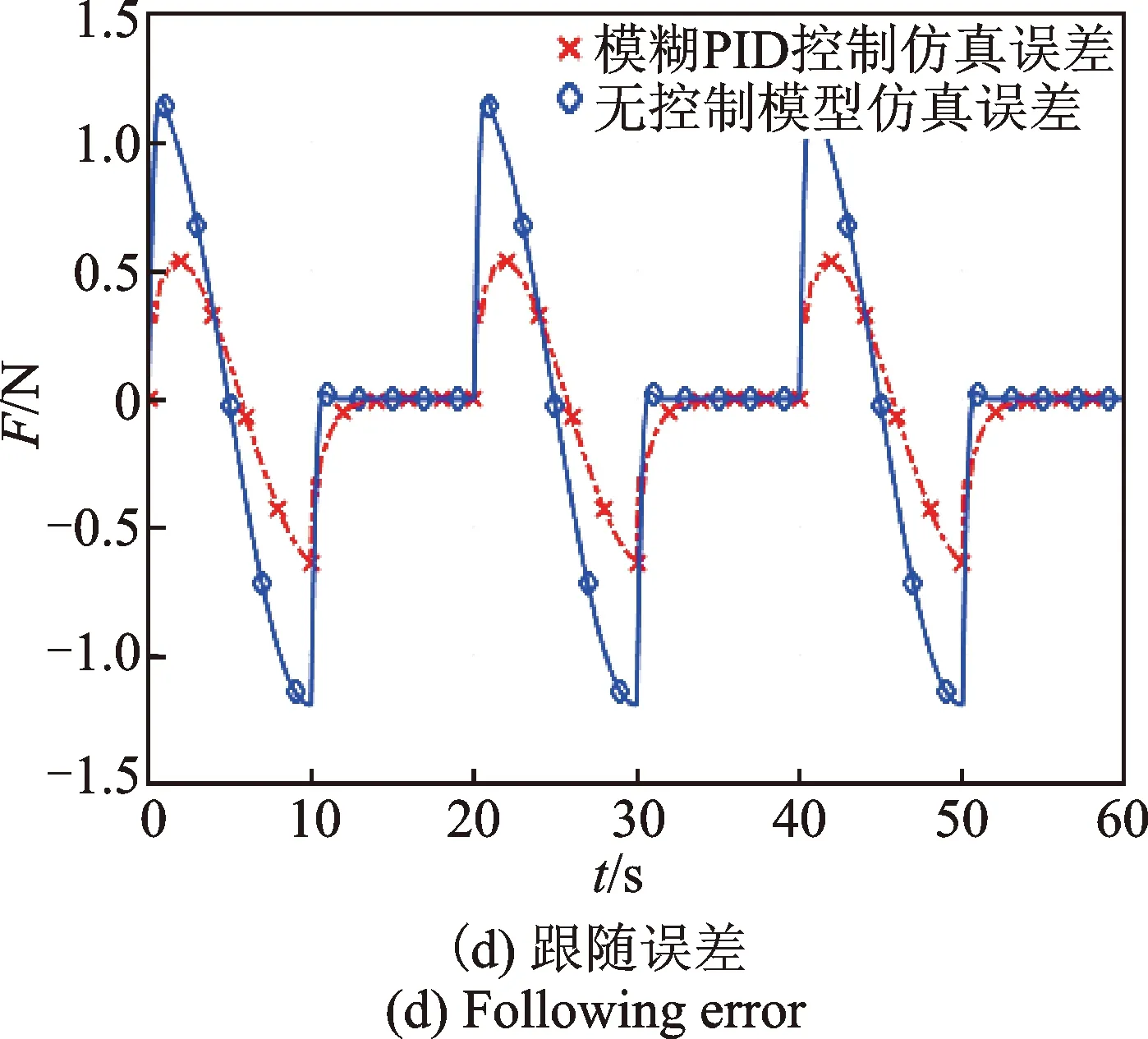
图14 正向正弦跟随仿真Fig.14 Forward sine following simulation

降低给定信号频率，采用频率为0.05Hz、幅值为10 N的正弦信号作为给定输入信号。考虑力控法兰控制信号不小于0，将正弦输入信号的负值部分过滤后进行仿真，获得仿真结果如图14所示。图14(a)为前3个周期的响应曲线，从整体来看系统跟随性良好。图14(b)～(c)分别为响应曲线起点和顶点的局部放大图。可以看出，加模糊PID控制后，在起点处稍有振荡然后迅速进入跟随状态，且其响应曲线延迟明显小于无模糊PID控制的响应曲线。从图14(d)可知，加模糊PID控制之后，力控法兰仿真的输出力跟随误差由±1.2 N减小为±0.6 N。综合以上，加模糊PID控制器后，系统的动态调节性能及跟随鲁棒性明显改善。

4.2 实验验证

为了进一步验证模糊PID控制器对力控法兰装置动态性能的影响以及其跟随鲁棒性，搭建基于Labview的力控法兰半实物实验平台，如图15所示。平台主要由力控法兰装置、PCI1710u数据采集卡及其接口板和计算机组成。实验中，为了尽量减少其他非线性因素对实验的影响，使力控法兰装置保持垂直向下的状态，不连接加工工具，可以不考虑法兰在加工运行中由位姿变化引起的受力变化和固定在法兰末端的工具重力。需要进行两组实验：a.阶跃响应实验,在实验中设定目标力F=10 N，给定气泵压力为0.7MPa，分别记录加模糊PID控制前后力控法兰输出力反馈值;b.正弦响应实验,选择幅值为10、频率为0.05Hz的正弦波信号，截取其正向部分作为控制器的给定信号，数据采集卡采集周期为10 ms，分别记录加模糊PID控制前后力控法兰输出力的反馈值。

图15 力控法兰实验平台Fig.15 Force-controlled flange experimental platform

阶跃响应实验响应曲线结果如图16所示。设定力控制信号F=10 N，两种情况下获得的末端输出力的响应曲线如图16所示。虽然采集的数据受噪声干扰存在一定的波动，但仍可以看出，增加模糊PID控制器后，力控法兰响应时间明显减小，其动态调节性能显著提升。

图16 加模糊PID控制前后阶跃响应实验曲线对比Fig.16 Comparison of experimental curves of step response before and after fuzzy PID control

正弦跟随实验结果如图17所示。图17(a)显示无模糊PID控制时，响应曲线延迟明显，加模糊PID控制器后，响应曲线延迟减小，与给定信号基本重合。响应曲线跟踪误差如图17(b)所示，跟踪误差由大约±3 N减小为大约±1.5 N。可见，实验结果与仿真结果相符。增加模糊PID控制器后，力控法兰的动态响应性能及跟随控制性能得到了提高，系统具有较强的鲁棒性。

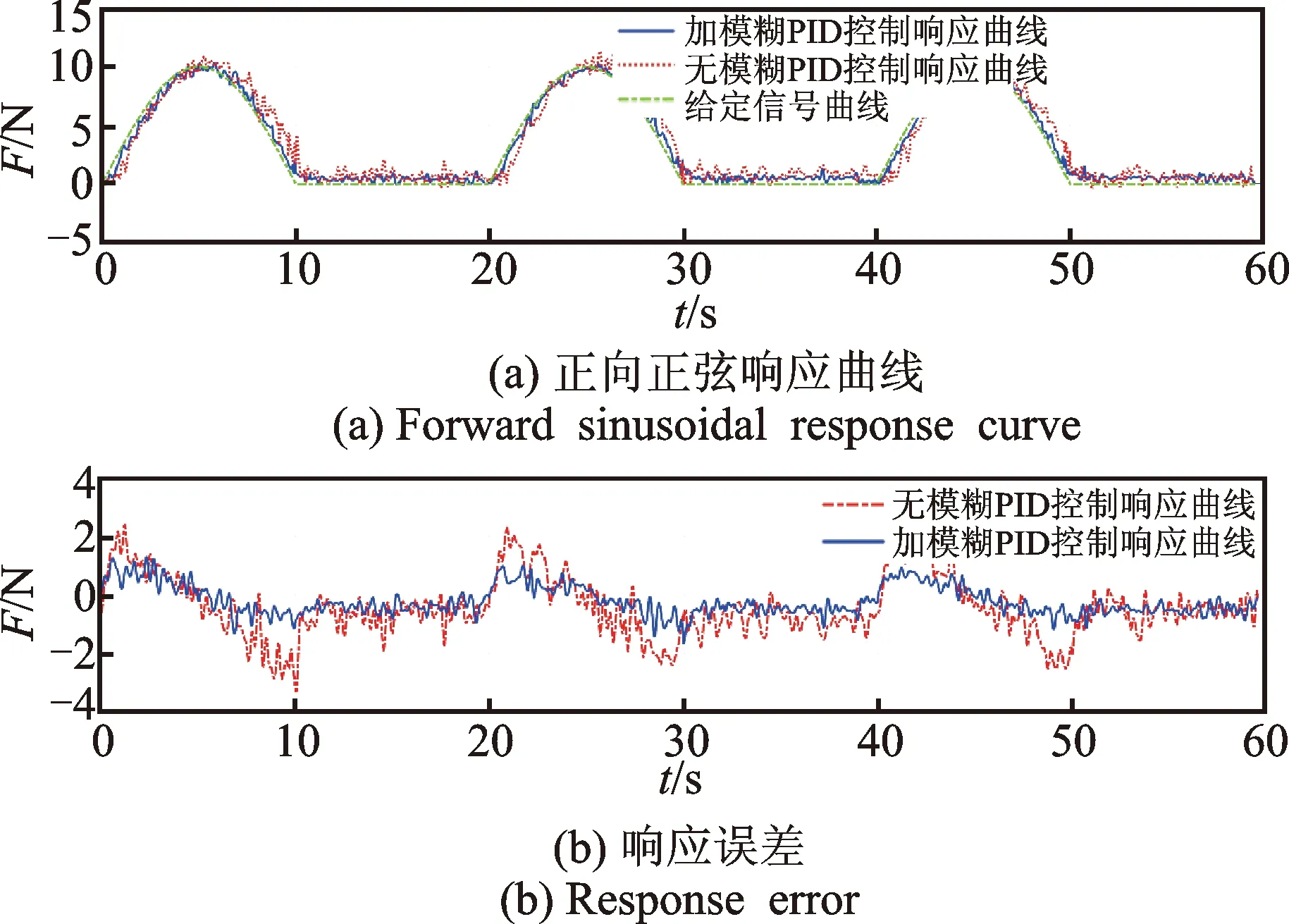
图17 正向正弦响应实验结果Fig.17 Experimental results of forward sinusoidal response

为了更直观地验证力控法兰的末端输出力控制的稳态鲁棒性，将力控法兰装置安装于机器人末端，另一端安装打磨工具。在铝合金工件上实际运行一条加工轨迹。设定法兰接触力为F=10 N，运行过程中保持工具与工件的法向接触，工具的重力根据运行的姿态进行重力补偿。得到末端输出力反馈数据如图18所示。最终实际接触力在期望力的±0.8 N范围内波动，输出力控制稳定性较好。

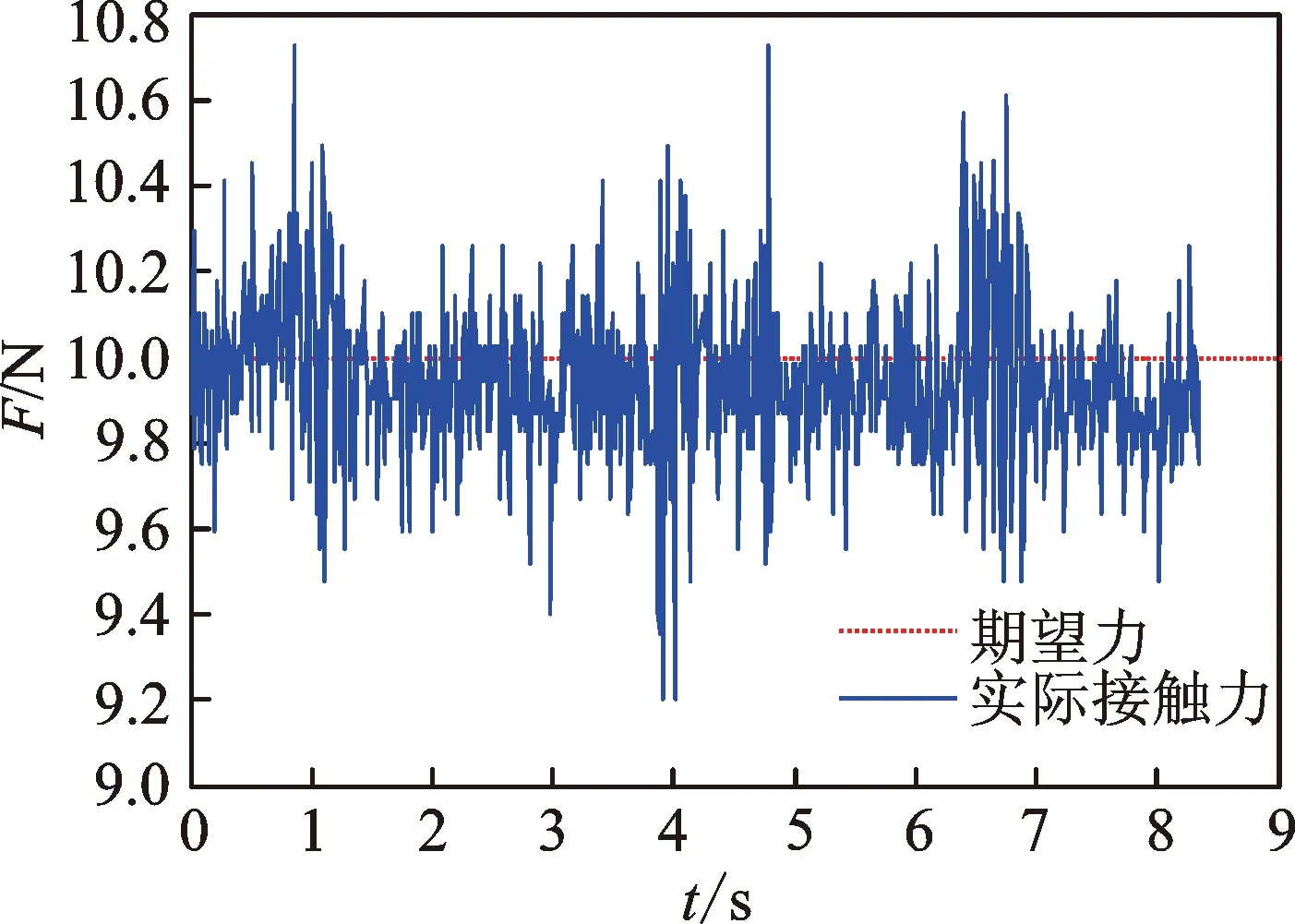
图18 力控法兰输出力测试Fig.18 Output force test of force-controlled flange

5 结束语

针对机器人进行接触式作业的过程中对工具末端与工件的接触力的要求，提出了一种基于模糊PID控制的力控法兰恒力控制方法。通过理论分析对该装置进行了建模，并通过实验测定法获得了该装置的近似模型。设计了一种模糊控制与PID控制并行的模糊PID控制器，对系统的动态调节性能进行了优化。仿真结果表明，模糊PID控制器可提高系统的响应时间，并对末端输出力进行有效跟踪。搭建基于Labview的半实物仿真平台，对力控法兰进行控制实验。实验进一步证明了仿真结果，动态响应时间缩短，动态性能明显优化。正弦跟踪实验最大跟踪误差小于1.5 N，证明控制器控制稳定性良好,具有较强的鲁棒性。最后，通过接触加工实验对输出力进行检测，验证了系统具有对末端力的恒力控制能力。

[1] 王田苗,陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报,2014,50(9):1-13.

Wang Tianmiao,Tao Yong.Research status and industrialization development strategy of Chinese industrial robot[J].Journal of Mechanical Engineering,2014,50(9):1-13.(in Chinese)

[2] Valente A.Reconfigurable industrial robots:a stochastic programming approach for designing and assembling robotic arms[J].Robotics and Computer-Integrated Manufacturing,2016,41:115-126.

[3] Chen Yonghua,Dong Fenghua.Robot machining:recent development and future research issues[J].International Journal of Advanced Manufacturing Technology,2013,66(9-12):1489-1497.

[4] 吴石,刘献礼,宋盛罡,等.铣刀磨损对铣削稳定性及表面位置误差的影响[J].振动、测试与诊断,2015,35(4):763-769.

Wu Shi,Liu Xianli,Song Shenggang,et al.The influence of wear loss of milling cutter on milling stability and surface location error[J].Journal of Vibration,Measurement &Diagnosis,2015,35(4):763-769.(in Chinese)

[5] Siciliano B,Sciavicco L,Villani L,et al.Robotics:modelling,planning and control[M].[S.l.]:Springer Publishing Company,Incorporated,2010:363-371.

[6] 孔民秀,游玮,杜志江,等.基于速度闭环的自适应力位控制算法[J].哈尔滨工业大学学报,2010,42(3):409-413.

Kong Minxiu,You Wei,Du Zhijiang,et al.Adaptive force/position control algorithm with closed loop of velocity for the haptic device[J].Journal of Harbin Institute of Technology,2010,42(3):409-413.(in Chinese)

[7] Chaudhary H,Panwar V,Prasad R,et al.Adaptive neuro fuzzy based hybrid force/position control for an industrial robot manipulator[J].Journal of Intelligent Manufacturing,2016,27:1-10.

[8] Sakaino S,Sato T,Ohnishi K.Force-based disturbance observer for dynamic force control and a position/force hybrid controller[J].Ieej Transactions on Electrical &Electronic Engineering,2013,8(5):505-514.

[9] Hogan N.Impedance control-an approach to manipulation.I-theory.II-implementation.III-applications[J].Journal of Dynamic Systems Measurement &Control,1985,107(1):1-24.

[10]Huang Han,Gong Zhiming,Chen Xiaoqi,et al.Robotic grinding and polishing for turbine-vane overhaul[J].Journal of Materials Processing Technology,2002(127):140-145.

[11]Jin Mingsheng,Ji Shiming,Pan Ye,et al.Effect of downward depth and inflation pressure on contact force of gasbag polishing[J].Precision Engineering,2017,47:81-89.

10.16450/j.cnki.issn.1004-6801.2017.04.002

* 国家科技支撑计划资助项目(2015BAF10B00)

2017-06-10;

2017-06-30

TP273.4

黄婷，女，1984年10月生，博士、工程师。主要研究方向为工业机器人控制与应用。曾发表《小功率随动系统的建模与校正网络设计》(《南昌航空大学学报：自然科学版》2008年第22卷第1期)等论文。 E-mail：hting104@163.com