高转速下主轴-双面锁紧刀柄接触特性预估*
赵永胜,许静静,蔡力钢,刘志峰
(北京工业大学机械工程与应用电子技术学院 北京,100124)
高转速下主轴-双面锁紧刀柄接触特性预估*
赵永胜,许静静,蔡力钢,刘志峰
(北京工业大学机械工程与应用电子技术学院 北京,100124)
采用有限元方法获得不同转速下端面和锥面的接触压强,基于该压强采用三维分形和赫兹接触理论计算双面锁紧刀柄与主轴的接触刚度,建立高转速下主轴-双面锁紧刀柄系统仿真模型。分析不同参数对主轴-双面锁紧刀柄(BTF40)系统锥面接触率及结合部接触刚度的影响规律,确定了该新型刀柄的极限转速、拉刀力、碟簧刚度和碟簧预紧力的合理取值区间,研究结果为双面锁紧刀柄的设计与优化提供了理论依据。
双面锁紧刀柄;高转速;三维分形理论;接触刚度
引 言
刀柄是连接机床主轴与刀具的重要单元,主轴-刀柄结合部是该系统的薄弱环节之一,其接触特性直接影响系统联接可靠性及加工精度。国内外学者对刀柄-主轴接触特性的研究主要有基于子结构耦合的频响函数辨识方法(receptance coupling substructure analysis,简称RCSA)和有限元仿真分析法。Tsutsumi等[1-2]通过实验和有限元相结合的方法研究了不同刀柄-主轴系统的刚度特性及拉刀力对刀柄抗弯刚度和轴向位移的影响,确定了拉刀力最佳取值。Aoyama等[3]提供了一种测量高转速下结合部径向刚度的方法,分析了不同转速和不同径向力对型号为HSK和BT刀柄结合部的径向刚度的影响。Schmitz等[4-5]采用子结构耦合辨识方法辨识主轴-刀柄结合面刚度,该方法通过锤击实验方法结合最小二乘理论算法辨识刀柄-主轴结合面刚度阻尼参数,并在此基础上预测刀尖点的频响函数。该方法受测试环境影响较大,无法获得高转速条件下的主轴-刀柄系统频响函数,其应用受到限制。
基于微观建模与有限元分析相结合的方法[6]是近年研究的热点,其中接触表面微观建模成为关键。分形接触理论是一种有效的微观建模方法,该方法最大特点是接触面表征参数(分形维数D,分形粗糙度参数G)具有尺度独立性,即不受仪器分辨率和取样长度的影响。文献[7]基于分形表征函数(W-M函数[8])建立了M-B分形模型。文献[9-10]以此为基础进行改进,为了准确预估结合面接触参数,Wang等[11]引入了包含域扩展因子的微接触点大小分布函数。文献[12]以M-B分形模型为基础建立了三维分形模型。上述研究为主轴-刀柄系统高转速下接触特性研究提供了一种有效途径。
笔者基于宏微观相结合的方法建立高转速下主轴-双面接触刀柄的仿真模型。宏观上假设接触表面为理想光滑表面,采用有限元方法获得其表面压强分布;微观上以三维分形接触理论计算表面的接触刚度。基于建立的模型来分析不同参数对双面锁紧刀柄-主轴系统接触特性的影响,从而确定该双面锁紧刀柄的转速上限值及拉刀力、碟簧刚度、预紧力的合理取值范围,研究结果为双面锁紧刀柄的优化与应用提供了理论依据。
1 接触表面刚度建模
与M-B分形接触模型相似,该三维分形模型假设粗糙表面各向同性,且微凸体间无相互作用力。同时,为使接触刚度预估值更加准确,在三维微凸体截面积大小分布函数中引入拓展域因子ψ,并将微凸体变形分为完全弹性阶段、弹塑性变形阶段及完全塑性阶段。
单个微凸体曲率半径R及法向变形量δ分别[10]为
其中:a′为单个微凸体横截面积;r′为截面积半径;r′2=2Rδ(R≫r′);γ为尺度参数,考虑到表面平整度及频谱分布密度考虑,γ=1.5。
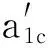
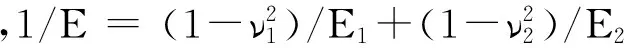
根据L-L模型[13],由弹塑性变形向塑性变形转变时,其临界变形量δ2c为
δ2c=76.4δ1c
(5)
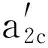
(6)
修正后的二维微凸体横截面积分布函数为
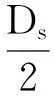
其中:Ds为二维分形维数;ψ为拓展域因子。
基于粗糙表面各向同性的假设,三维分形维数D=Ds+1,则三维微凸体横截面积大小分布函数为
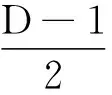
(7)
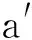
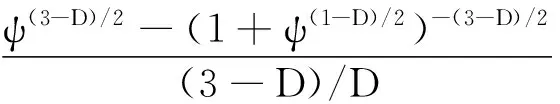
1.1 接触表面法向载荷
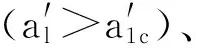
基于微凸体截面积大小分布函数在各变形区域分别进行积分,加和得到总接触表面法向载荷为
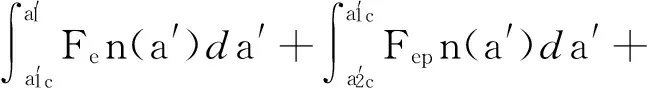
(11)
接触表面名义压强可表示为
(12)
1.2 接触表面分形接触刚度
1.2.1 法向接触刚度
由赫兹理论可知,单个微凸体的法向接触刚度为
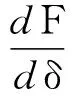
(13)
式(7)在各变形阶段分别进行积分,结合面法向接触刚度可表示为
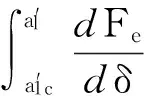
(14)
1.2.2 切向接触刚度
单个微凸体的切向变形[14]为
(15)
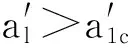
单个微凸体的切向接触刚度为
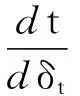
(16)
在完全弹性阶段与弹塑性阶段下分别积分,接触表面切向接触刚度可表示为
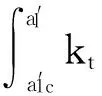
(17)
2 双面锁紧刀柄-主轴系统仿真模型
双面锁紧刀柄由刀柄本体、碟簧和锥套组成,其在高转速状态下通过碟簧自动调整刀柄锥面和主轴内锥面、以及刀柄端面与主轴端面之间的压力,从而始终保持刀柄锥面、端面与主轴内锥面、端面的相互锁紧状态,如图1所示。双面锁紧刀柄-主轴系统中主轴与刀柄材料均为20CrMo,其弹性模量为2.06×1011Pa,泊松比为0.28,材料屈服强度为1 300 N/mm2,锥面和端面粗糙度均为0.4。采用表面轮廓扫描仪得到粗糙表面轮廓的三维数据,基于功率谱方法[15]获得该结合面各分形参数,其中二维分形维数Ds=1.36,表面粗糙度参数G=6.328×10-12m。假设结合表面各向同性,结合面三维分形参数D=Ds+1=2.36。主轴和刀柄结构尺寸参数如表1,2所示。
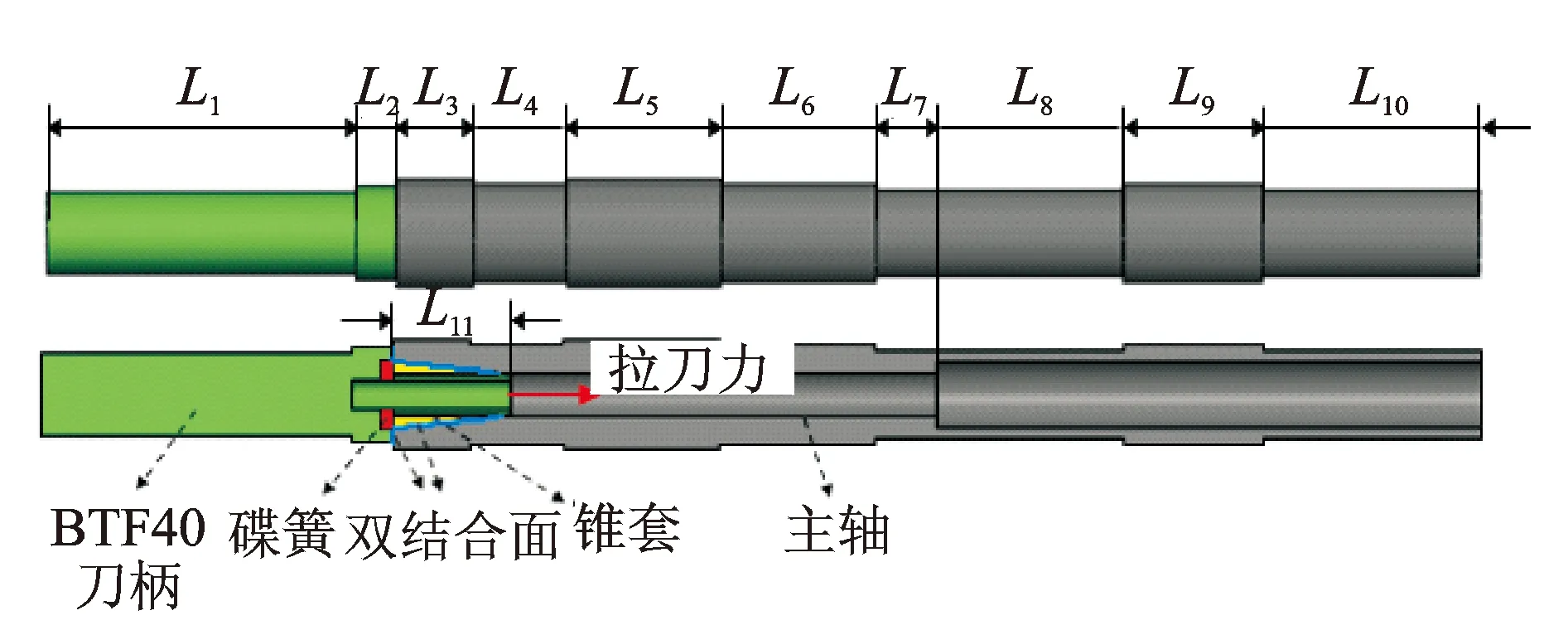
图1 BTF40刀柄-主轴系统简化几何模型Fig.1 The simplified geometry model of the BTF40 toolholder-spindle system
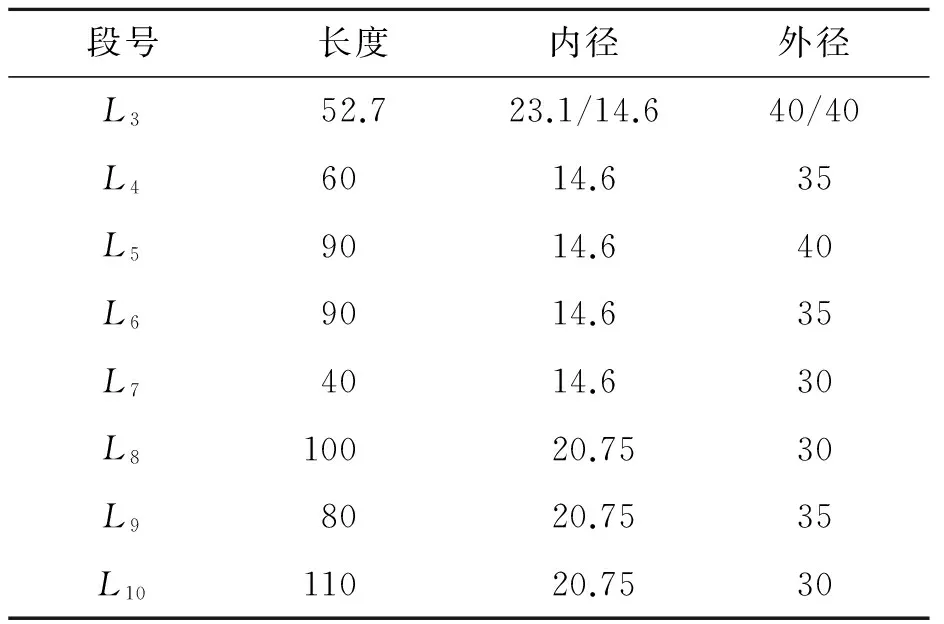
表1 主轴尺寸参数Tab.1 The dimension parameters of the spindle mm
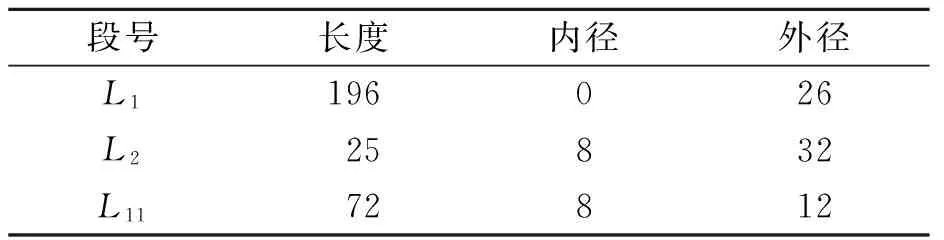
表2 刀柄尺寸参数Tab.2 The dimension parameters of the tool-holder mm
采用ANSYS仿真软件对该系统结构进行静力分析(主轴L4段轴向固定约束,施加拉刀力及碟簧预紧力)提取双结合面各节点压强。图2,3分别为刀柄端面和锥面的有限元网格(锥形与端面结合面上的网格数目分别为264与120)及无转速条件下双结合面压力云图(拉刀力为12 kN,碟簧刚度及预紧力分别为1.4 kN/mm及1 kN)。由图3可知,由于锥形结合面为旋转对称曲面,在距锥面大端相同距离的节点处压强基本相等,因此提取锥面某一母线上各节点的压强来体现锥面压强分布。
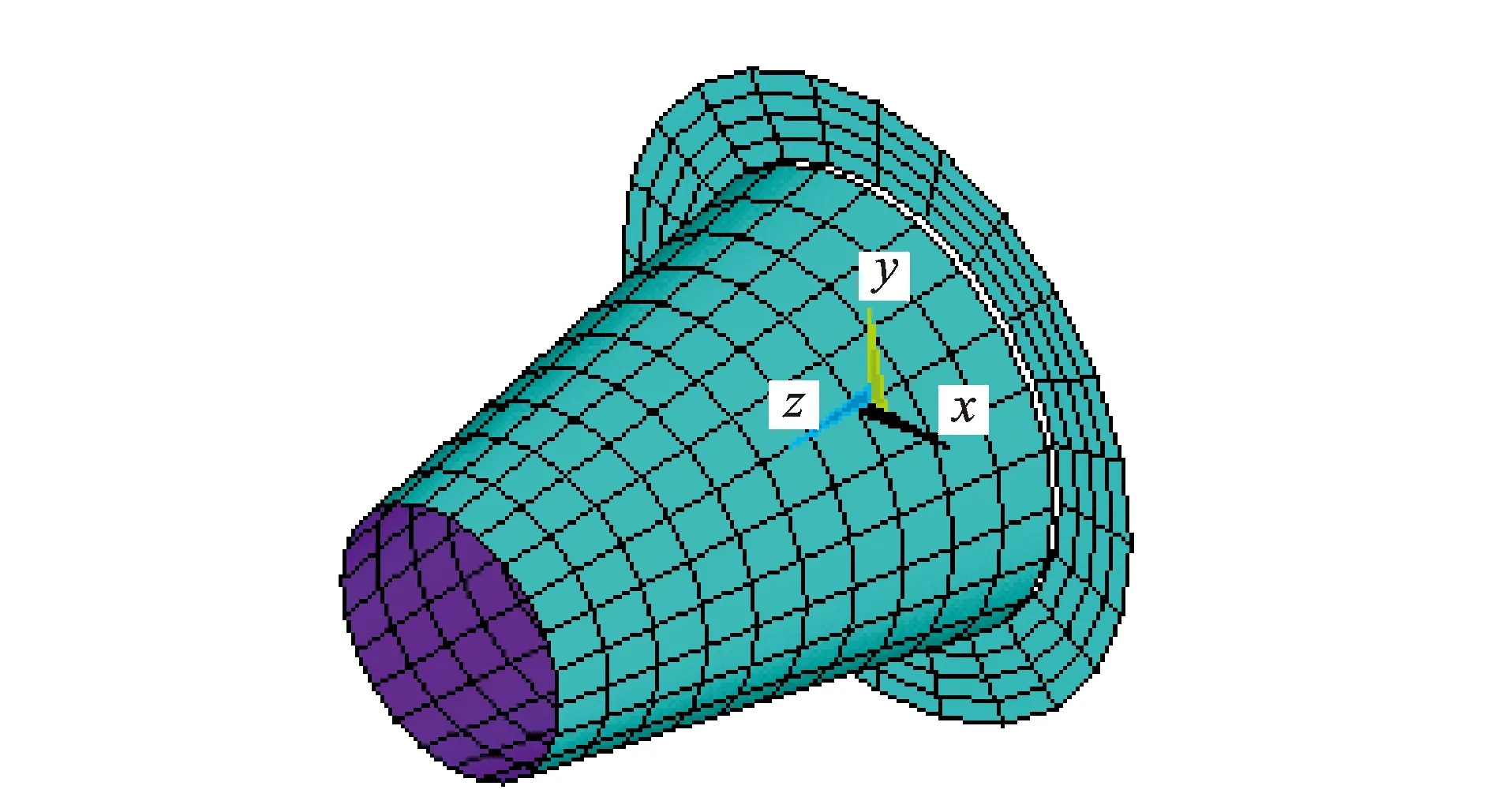
图2 端面和内锥面的有限元网格划分Fig.2 The mesh generation of the contact surfaces
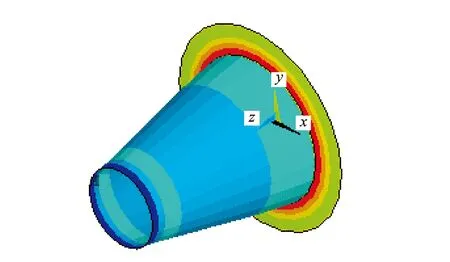
图3 结合面压力云图Fig.3 The pressure nephogram of the contact surfaces
由于结合部径向和扭转刚度是评价系统整体刚度的重要参数,需将双面锁紧刀柄接触表面的法向和切向接触刚度等效为结合部的扭转及径向刚度。图4为接触表面节点的法向及切向刚度示意图,A和B两点分别为锥面接触面与端面接触面上的节点。
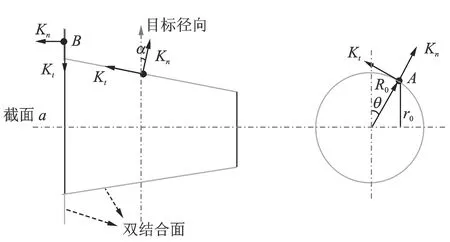
图4 双接触表面节点的法向及切向刚度示意图Fig.4 The schematic diagram of the nodal normal and tangential stiffness of the double contact surfaces
由于该模型为旋转体对称结构,则任取一径向为目标径向及轴截面a,计算等效径向刚度Ktt和扭转刚度Krr分别为
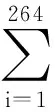
(18)
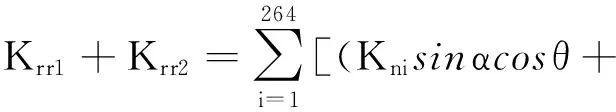
(19)
其中:Kni与Kti分别为锥形结合面上各节点处的法向刚度与切向刚度;Knj和Ktj分别为端面结合面上各节点的法向刚度与切向刚度;α,θ分别为锥面倾角与节点所在径向方向与目标径向之间的夹角;r0为节点所在位置距轴截面a的距离。
3 双面锁紧刀柄-主轴系统接触特性
高转速下,离心力、拉刀力、碟簧刚度和碟簧预紧力对双面锁紧刀柄-主轴系统联接可靠性及结合面刚度均有重要影响,需研究上述参数对结合部接触特性的影响。图5为双面锁紧刀柄-主轴系统接触特性分析流程图。基于该流程分别分析计算不同转速及高转速条件下,不同拉刀力、碟簧刚度和预紧力对应的锥面接触率及结合面等效扭转与径向刚度。
3.1 转 速
转速引起的离心力对系统联接可靠性及结合面承载能力有重要影响,研究不同转速下锥形结合面及端面结合面的接触应力情况及结合部扭转抗弯刚度系统接触特性参数变化趋势,为确定合理的转速上限提供依据。为研究不同转速对接触特性的影响,根据企业对该系统的使用参数经验值,拉刀力、碟簧刚度及碟簧预紧力分别取12 kN,1.4 kN/mm及1 kN。图6,7分别为不同转速条件下锥形结合面的节点压强分布及接触率。当转速为25 kr/min时,由于碟簧弹力与拉刀力对锥套的共同作用,使锥面中部发生局部分离且接触率为70%,该接触率为可保证刀柄-主轴系统的联接可靠性下限[16]。图8,9分别为转速对主轴-刀柄结合部等效扭转与径向刚度的影响规律。随着转速提高结合部扭转和径向刚度逐渐减小,在25 kr/min转速条件下扭转刚度与径向刚度与无转速工况下相比分别下降31.34%和32.41%。
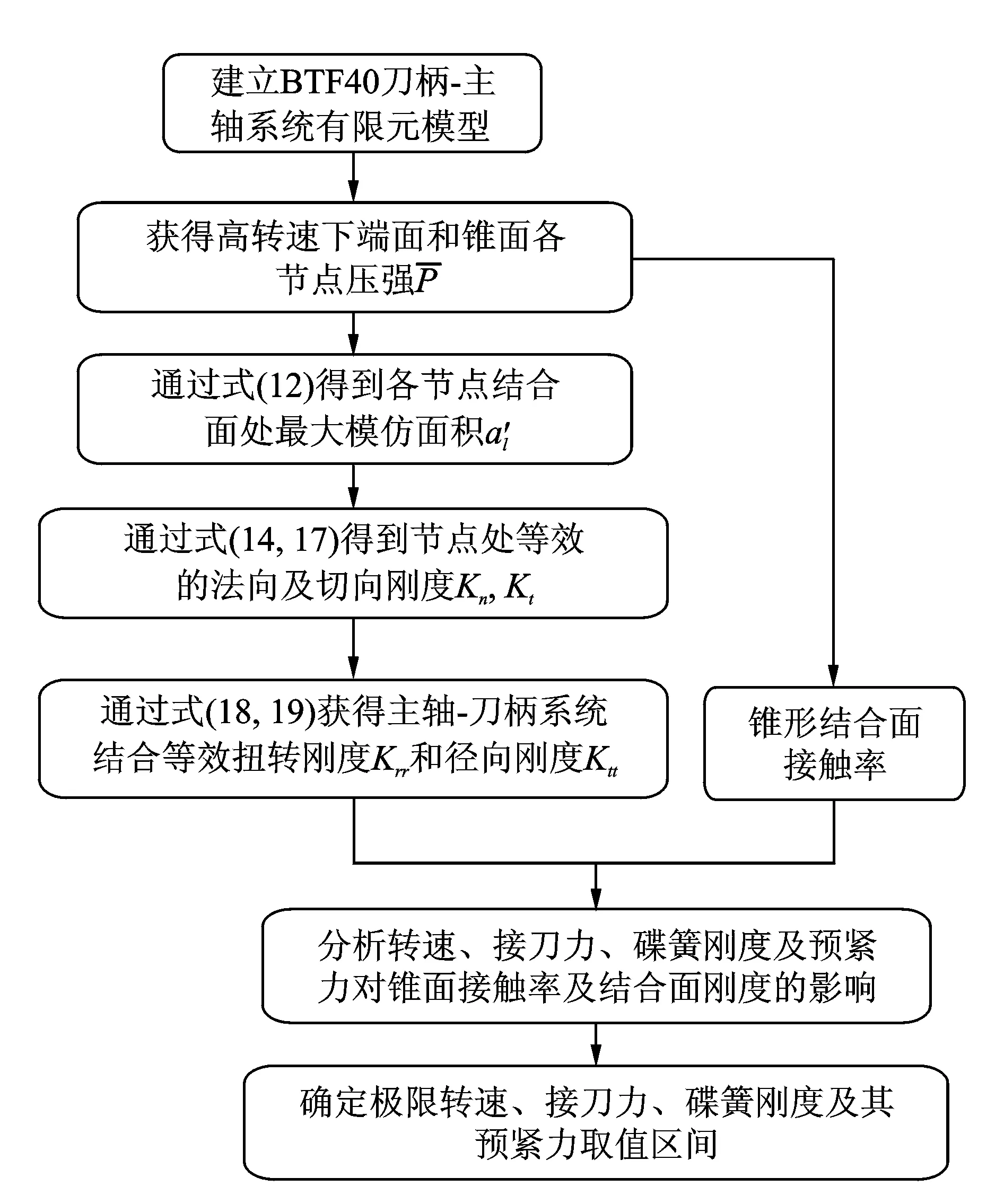
图5 双面锁紧刀柄-主轴系统接触特性分析流程图Fig.5 The flow chart of contact characteristic analysis of the double-locking toolholder-spindle system
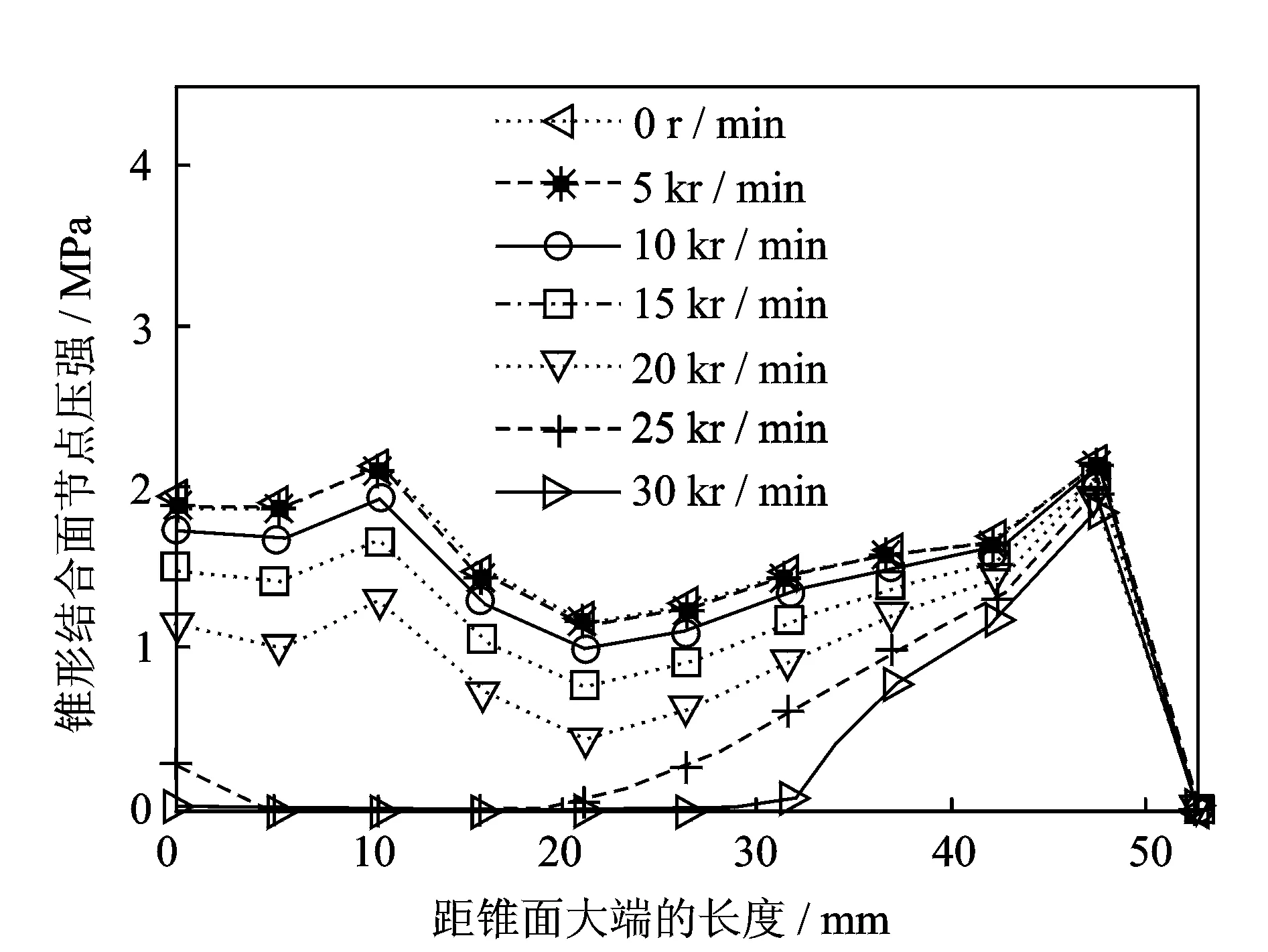
图6 不同转速下锥形结合面节点压强分布Fig.6 The taper-surface contact pressure distribution at different speeds
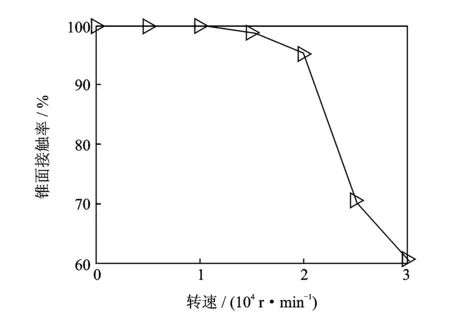
图7 转速对锥面接触率的影响Fig.7 The influence of speed on the taper-surface contact ratio
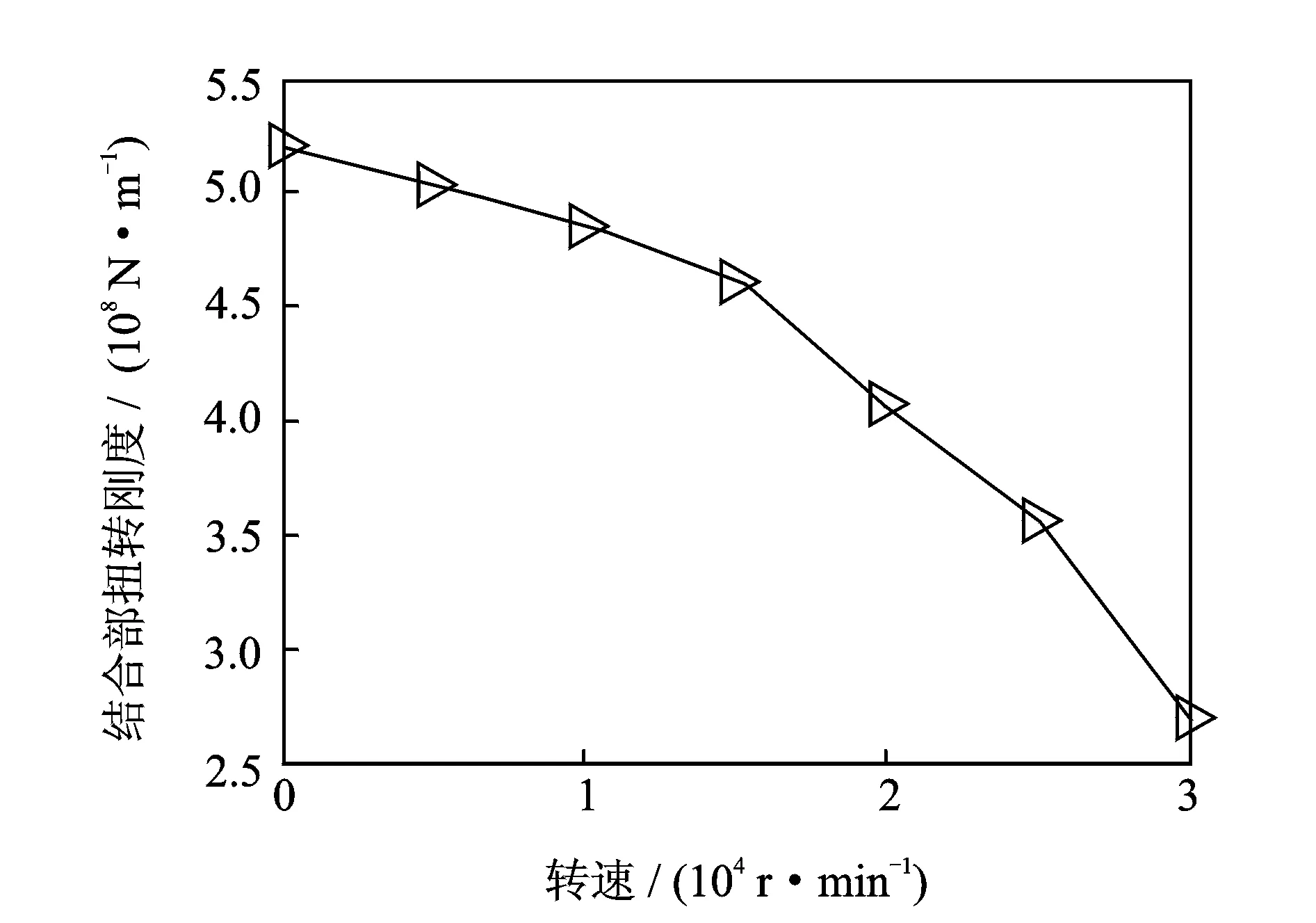
图8 转速对扭转刚度的影响Fig.8 The influence of speed on the torsional stiffness
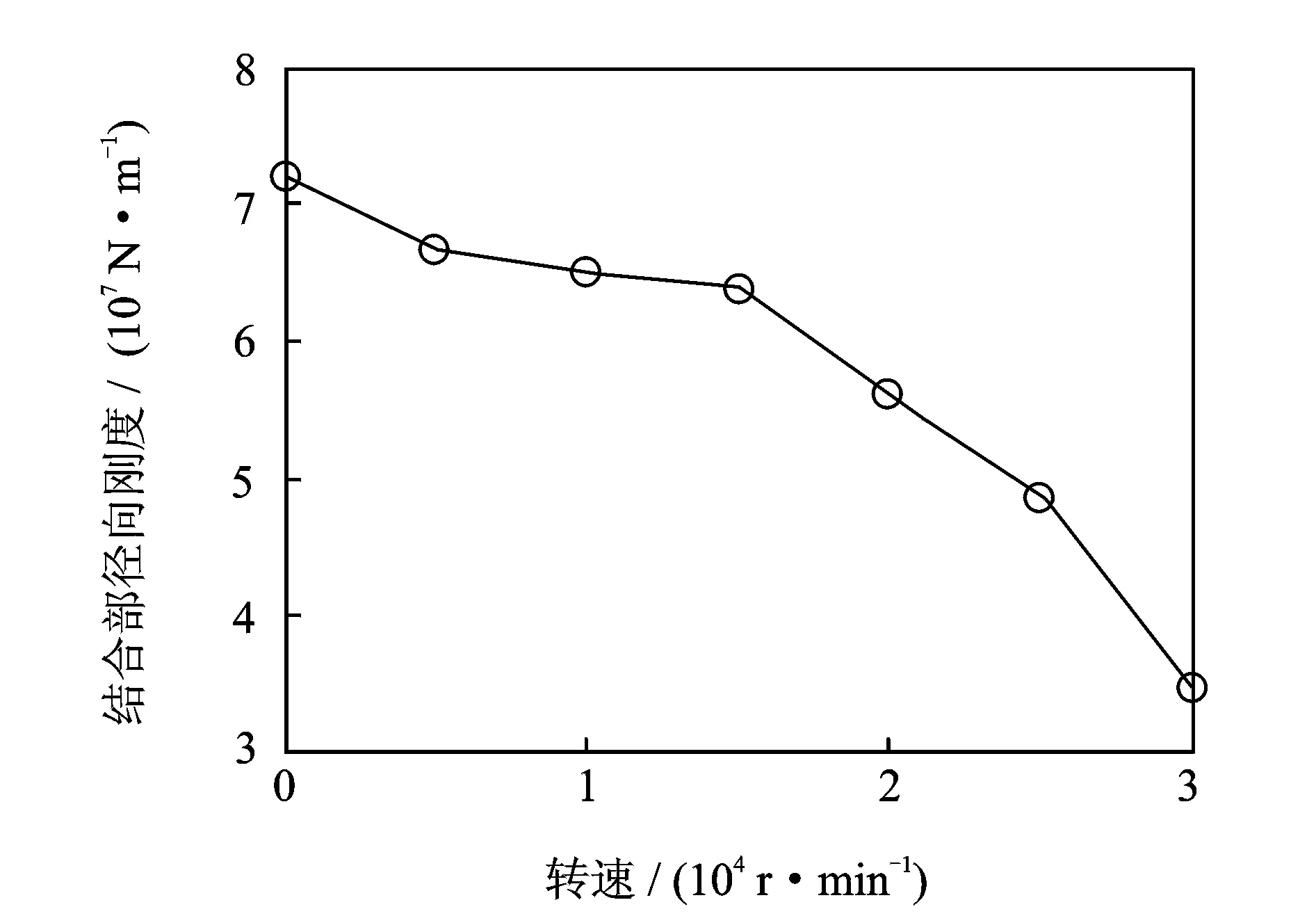
图9 转速对径向刚度的影响Fig.9 The influence of speed on the radial stiffness
3.2 拉刀力
拉刀力对主轴-刀柄系统接触特性有直接影响[1-2],拉刀力的增大导致结合面上的平均接触压力增大,结合面更易磨损,但同时又能提高其接触刚度和可靠性。为了研究高转速条件下拉刀力对锥形结合面接触率及结合部径向和扭转刚度的影响,分别取转速、碟簧刚度及预紧力分别为25 kr/min,1.4 kN/mm及1 kN。图10表示随着拉刀力的逐渐增大,锥形结合面中部的分离情况得到改善。由图11可知,拉刀力能够有效提高刀柄锥面的接触率,在转速为25 kr/min的条件下,当拉刀力小于10 kN时,接触率小于70%,系统联接不可靠。图12和图13为拉刀力对结合部扭转和径向刚度的影响规律,其随着拉刀力的增大而增大,但当拉刀力大于14 kN时,结合部刚度的增幅较小。因此,拉刀力应取为10 kN~14 kN。
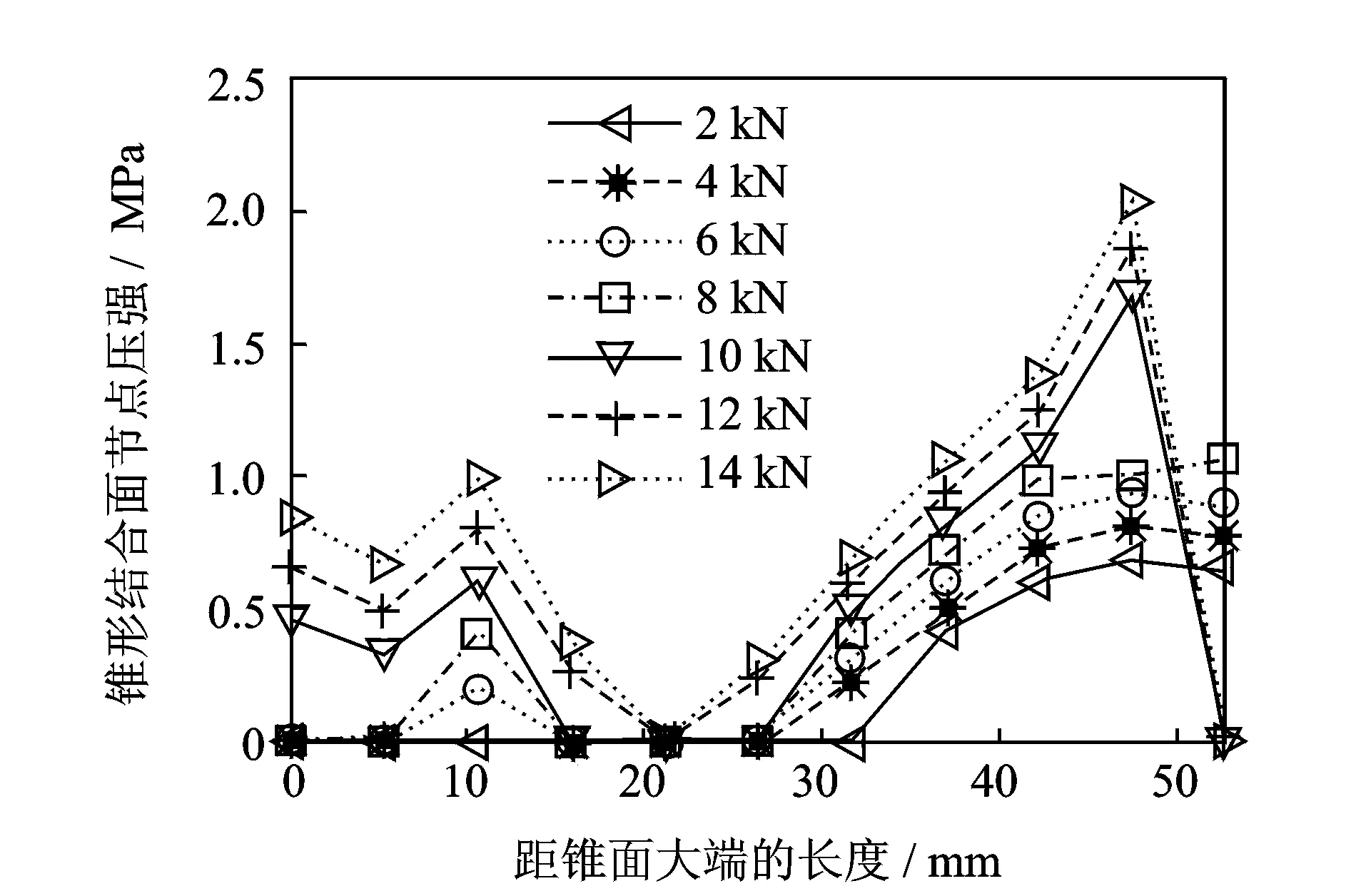
图10 不同拉刀力下锥形结合面节点压强分布Fig.10 The taper-surface contact pressure distribution at different draw-bar forces
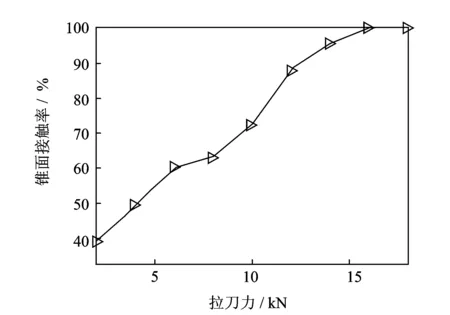
图11 拉刀力对锥面接触率的影响Fig.11 The influence of draw-bar force on the taper-surface contact ratio
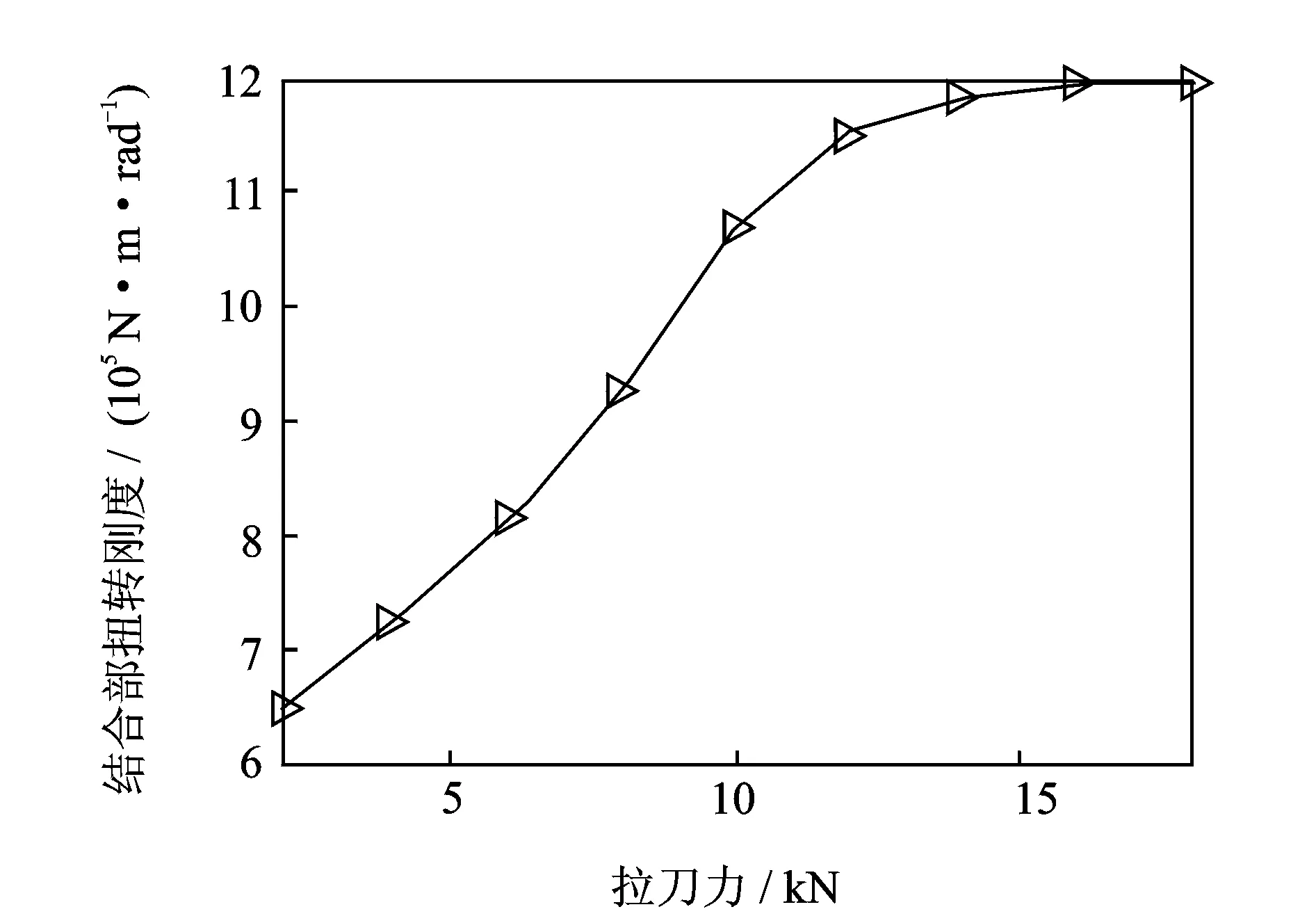
图12 拉刀力对扭转刚度的影响Fig.12 The influence of draw-bar force on the torsional stiffness
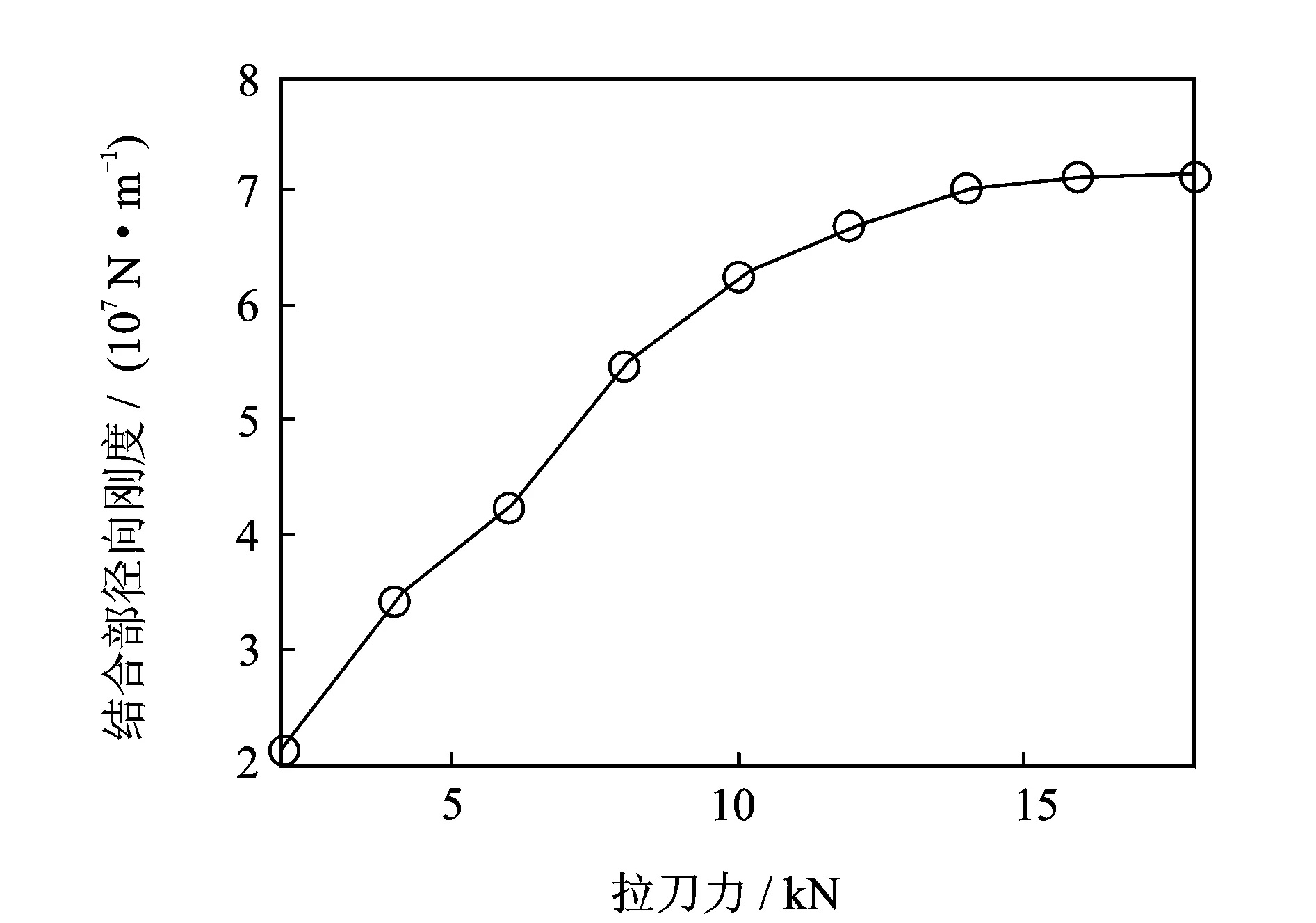
图13 拉刀力对径向刚度的影响Fig.13 The influence of draw-bar force on the radial stiffness
3.3 碟簧刚度
双面锁紧刀柄通过碟簧来调节锥面和端面的压力,碟簧刚度直接影响双面锁紧刀柄与主轴的接触状态,为研究高转速条件下碟簧刚度对系统接触特性的影响,分别选取转速、拉刀力及碟簧预紧力为25 kr/min,12 kN及1 kN。图14,15表明随着碟簧刚度的增大,锥面接触率也逐渐增大,当碟簧刚度为1.18 kN/mm时,锥面接触率增大到70.3%(满足系统可靠性联接要求)。图16和图17分别为碟簧刚度对扭转和径向刚度的影响规律,当碟簧刚度大于1.6 kN/mm时,随着碟簧刚度的增加,结合部的扭转和径向刚度变化较小。因此,碟簧刚度合理的取值范围为1.18 kN/mm~1.6 kN/mm。
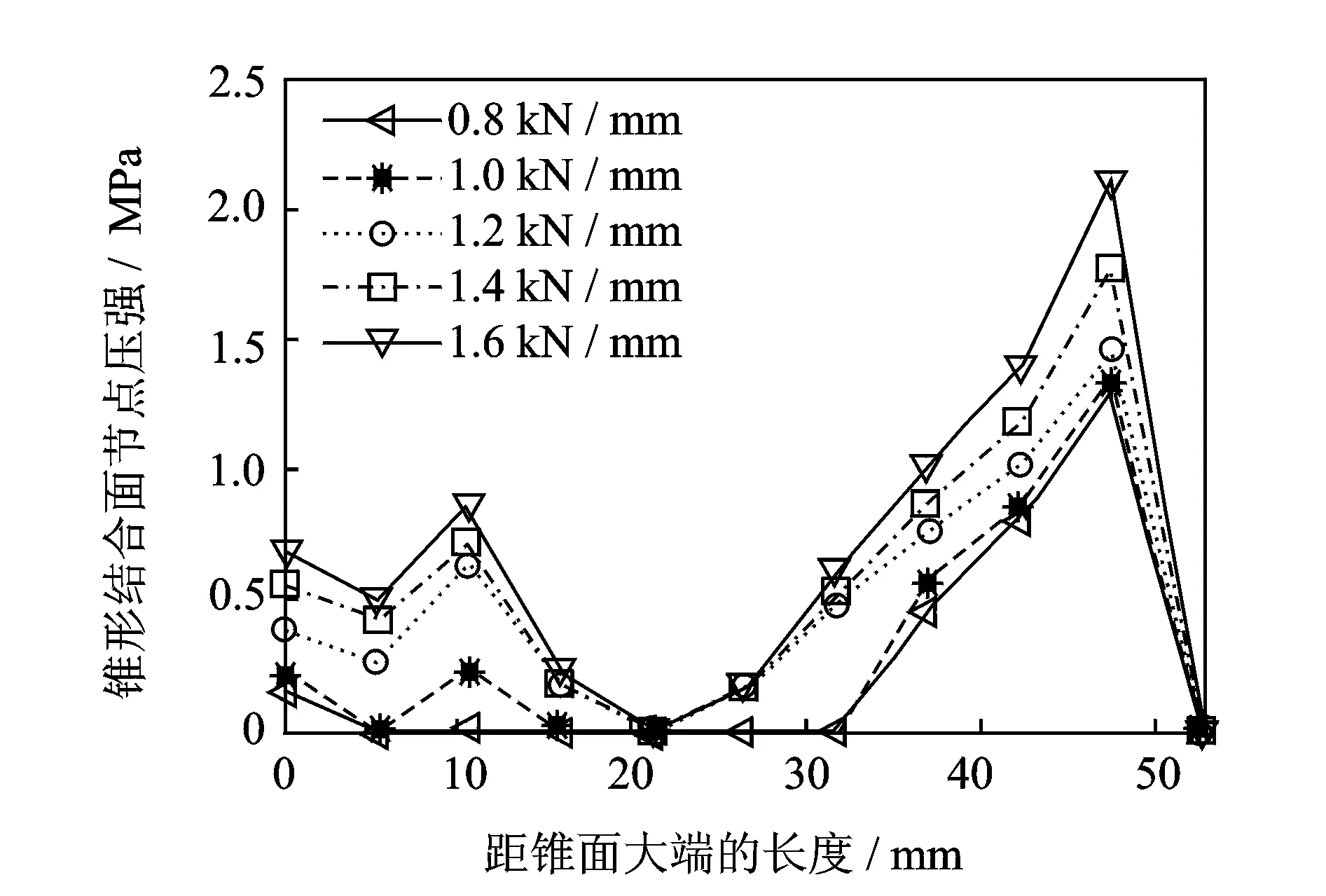
图14 不同碟簧刚度下锥形结合面节点压强分布Fig.14 The taper-surface contact pressure distribution at different disk-spring stiffness
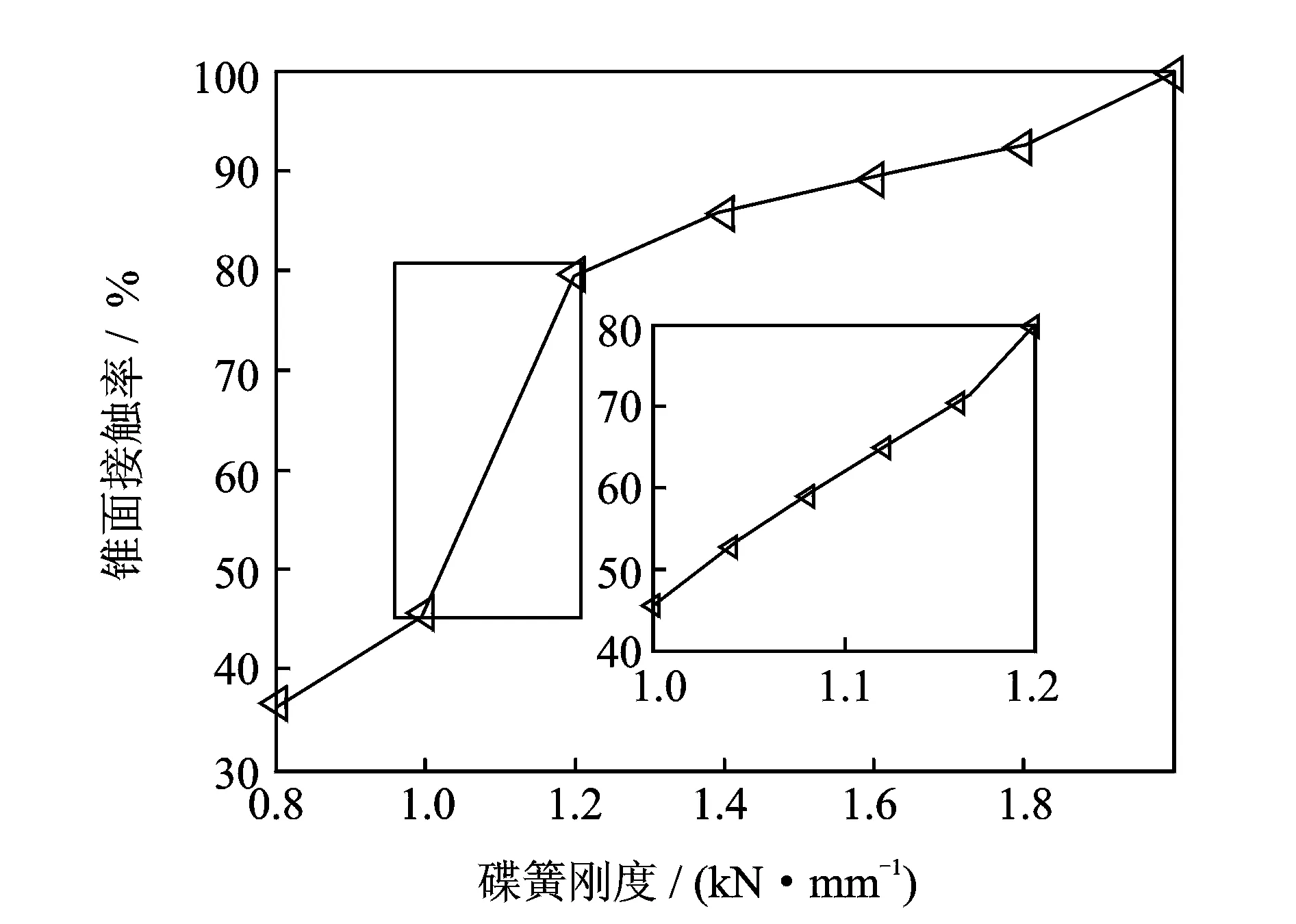
图15 碟簧刚度对锥面接触率影响Fig.15 The influence of disk-spring stiffness on the taper-surface contact ratio
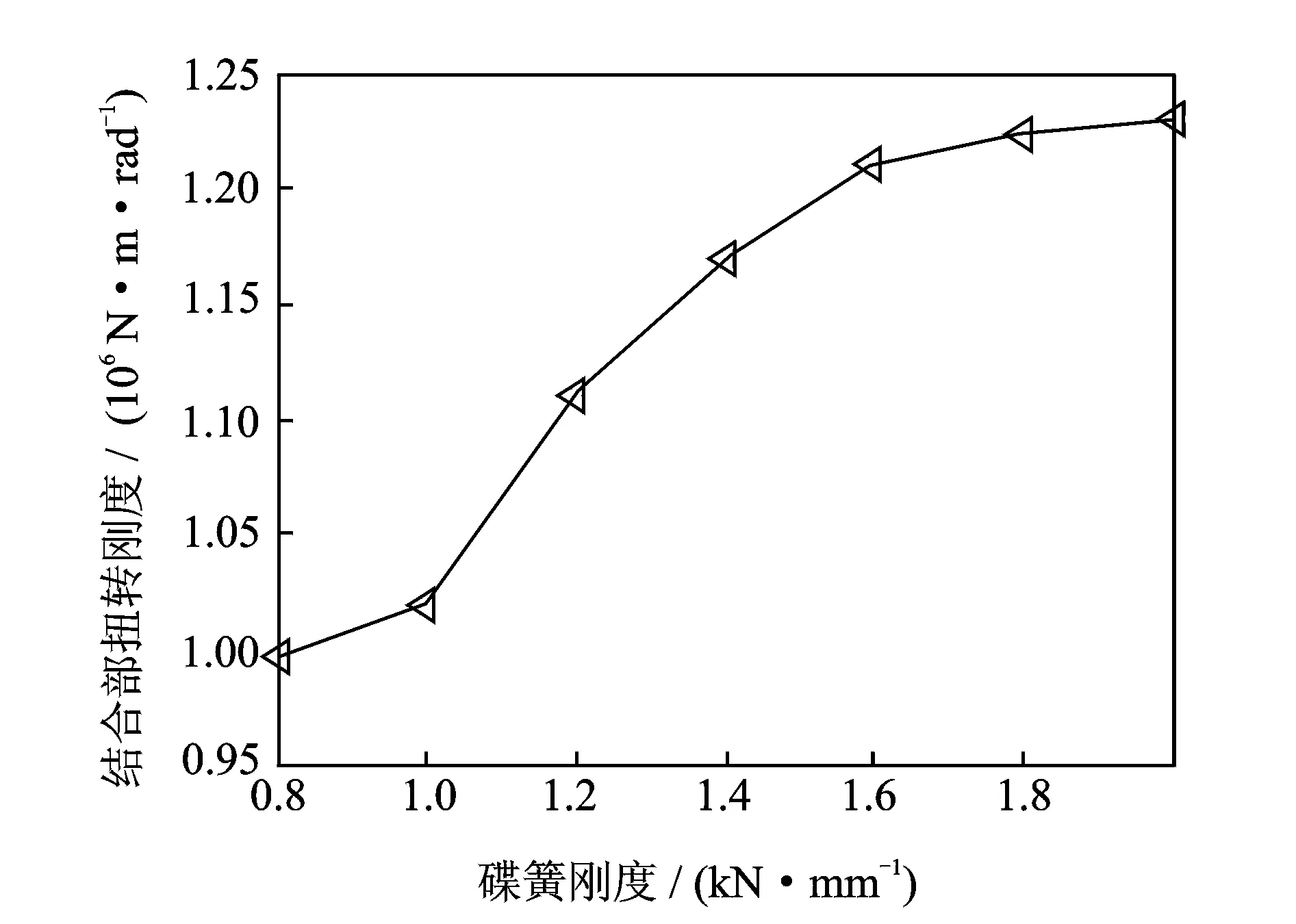
图16 碟簧刚度对扭转刚度的影响Fig.16 The influence of disk-spring stiffness on the torsional stiffness
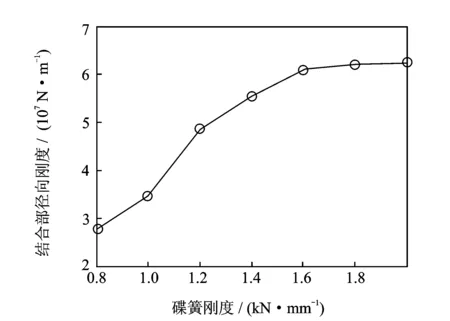
图17 碟簧刚度对径向刚度与的影响Fig.17 The influence of dis-spring stiffness on the radial stiffness
3.4 碟簧预紧力
为研究高转速条件下碟簧预紧力对系统接触特性的影响,取转速为25 kr/min,拉刀力及碟簧刚度分别为12 kN和1.4 kN/mm。图18,19为碟簧预紧力对锥面接触情况的影响规律。碟簧预紧力的增加能够提高锥面接触率,当碟簧预紧力为0.92 kN时,锥面接触率增大到71.4%,碟簧预紧力应大于0.92 kN。图20和图 21 分别为碟簧预紧力增大时结合部扭转刚度及径向刚度也随之增大,当碟簧预紧力大于1.2 kN时,结合部刚度变化幅度均较小,即碟簧预紧力对结合部刚度影响较小。可见,碟簧预紧力合理取值范围为0.92 kN~1.2 kN。
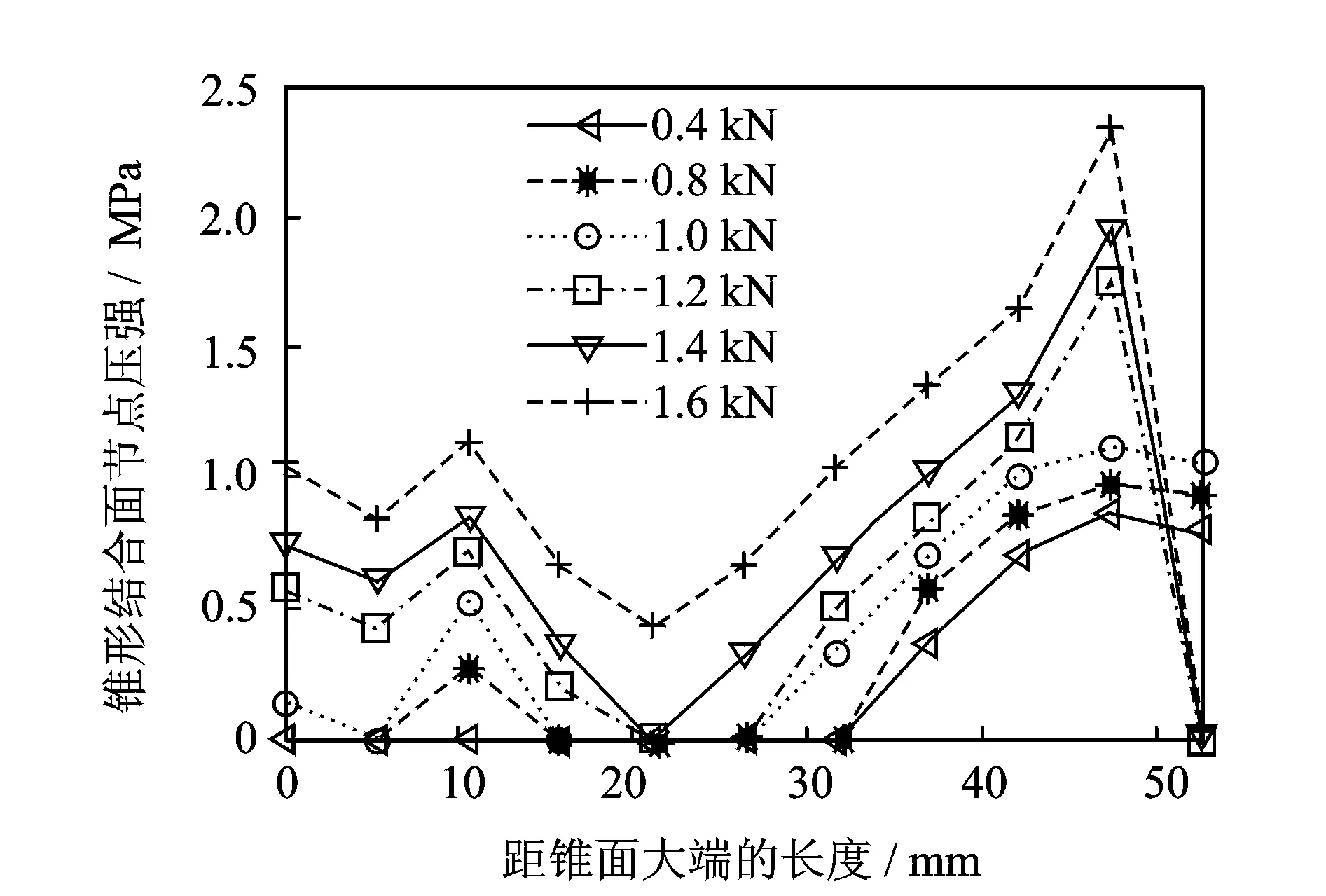
图18 不同碟簧预紧力下锥形结合面节点压强分布Fig.18 The taper-surface contact pressure distribution at different disk-spring pre-tightening forces
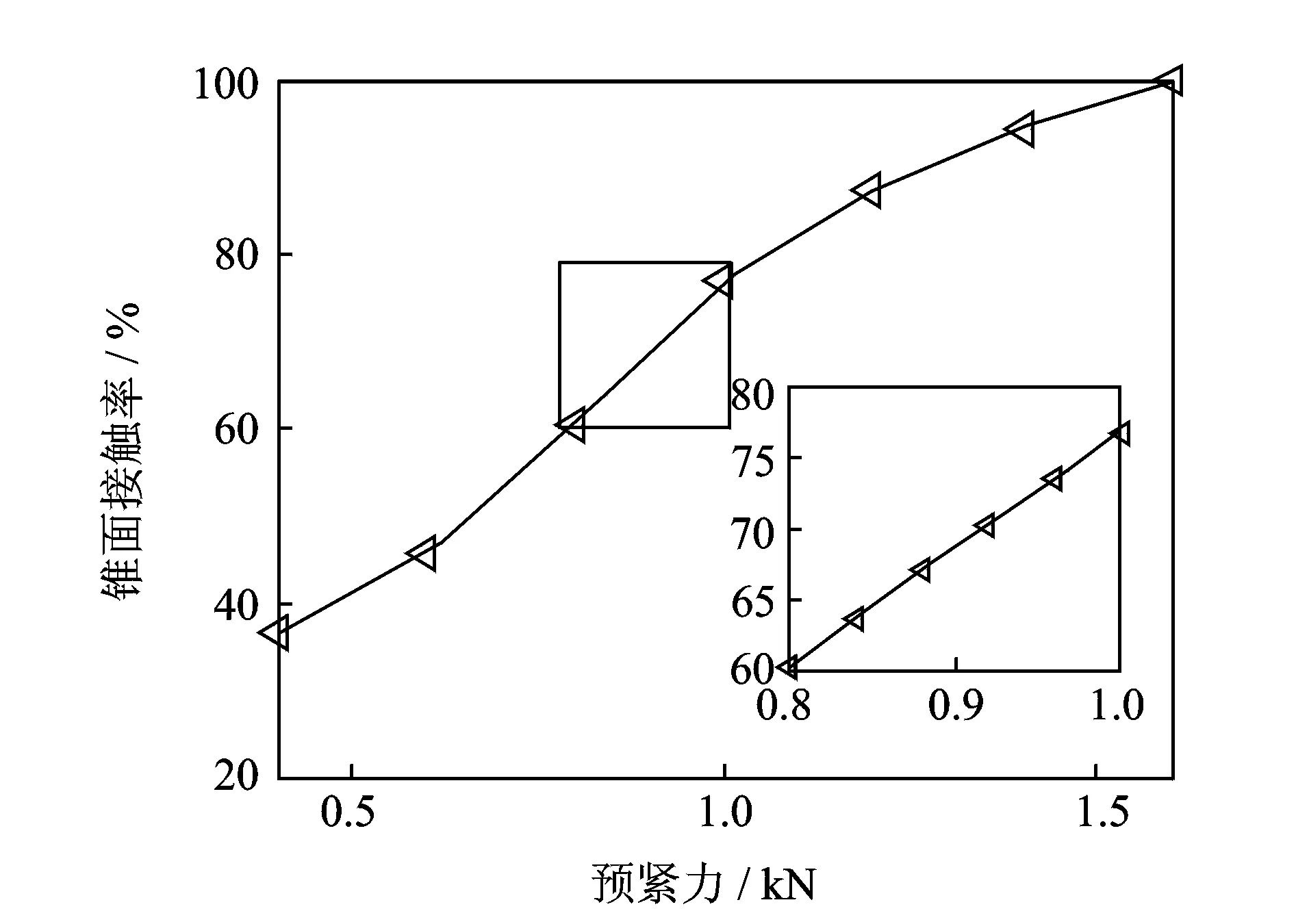
图19 碟簧预紧力对锥面接触率的影响Fig.19 The influence of disk-spring pre-tightening force on the taper-surface contact ratio
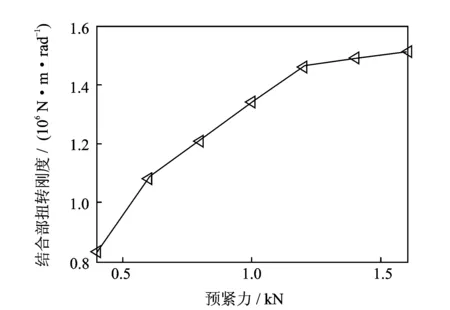
图20 碟簧预紧力对扭转刚度的影响Fig.20 The influence of disk-spring pre-tightening force on the torsional stiffness
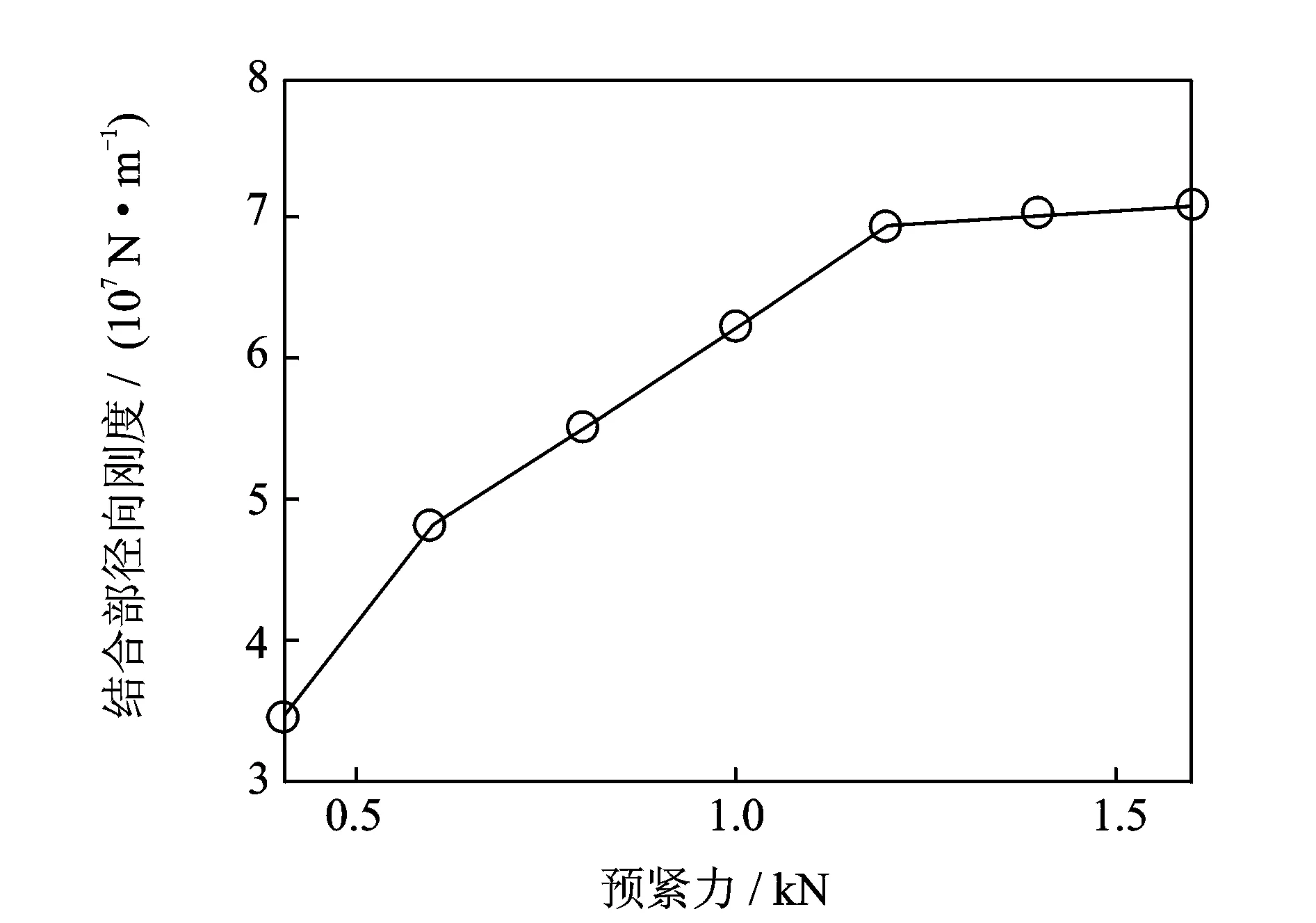
图21 碟簧预紧力对径向刚度的影响Fig.21 The influence of disk-spring pre-tightening force on the radial stiffness
4 结束语
提出宏微观相结合的方法建立高转速条件下双面锁紧刀柄(BTF40)-刀柄系统仿真模型,对其接触特性进行预估。结果表明:高转速下锥形结合部会发生分离,为保证主轴-刀柄系统联接可靠性,该刀柄工作极限转速为25 kr/min。分析了高转速条件下拉刀力、碟簧刚度和碟簧预紧力对锥面接触率、结合部径向和扭转刚度的影响规律,确定了拉刀力、碟簧刚度及预紧力的合理区间,分别为10 kN~14 kN,1.18 kN/mm~1.6 kN/mm和0.92 kN~1.2 kN。
[1] Tsutsumi M,Anno Y,Ebata N.Static characteristics of 7/24 tapered joint for machining center[J].Bulletin of the JSME,1983,26(213):461-467.
[2] Tsutsumi M,Kuwada Y,Shimizu S,et al.Static and dynamic stiffness of 1-10 tapered joints for automatic changing[J].International Journal of Japan Society of Precision Engineering,1995,30(4):301-306.
[3] Aoyama T,Inasaki I.Performances of HSK tool interfaces under high rotational speed[J].CIRP Annals Manufacturing Technology,2001,50(1):281-284.
[4] Schmitz T L,Donalson R R.Predicting high-speed machining dynamics by substructure analysis [J].CIRP Annals Manufacturing Technology,2000,49(1):303-308.
[5] Schmitz T L,Davies M A,Kennedy M D.Tool point frequency response prediction for high-speed machining by RCSA[J].Journal of Manufacturing Science and Engineering,2001,123(4):700-707.
[6] Zhao Yongsheng,Song Xiaolei,Cai Ligang,et al.Surface fractal topography-based contact stiffness determination of spindle-toolholder joint[J].Journal of Mechanical Engineering Science,2016,230(4):602-610.
[7] Majumdar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces [J].Journal of Tribology,1991,113(1):1-11.
[8] Majumdar A,Tien C L.Fractal characterization and simulation of rough surfaces[J].Wear,1990,136(2):313-327.
[9] 李小彭,郭浩,刘井年,等.考虑摩擦的结合面法向刚度分形模型及仿真[J].振动、测试与诊断,2013(2):210-213.
Li Xiaopeng,Guo Hao,Liu Jingnian,et al.Fractal model and simulation of normal contact stiffness considering the friction between joint surfaces[J].Journal of Vibration,Measurement &Diagnosis,2013(2):210-213.(in Chinese)
[10]牛作证,张学良,温淑花,等.结合面切向接触刚度三维分形模型[J].太原科技大学学报,2013,34(5):361-367.
Niu Zuozheng,Zhang Xuelaing,Wen Shuhua,et al.Three-dimensional fractal model of tangential contact stiffness of joint interfaces [J].Journal of Taiyuan University of Science and Technology,2013,34(5):361-367.(in Chinese)
[11]Wang S,Komvopoulos K.A fractal theory of the interracial temperature distribution in the slow sliding regime:part I-elastic contact and heat transfer analysis[J].Journal of Tribology,Transcations of ASME,1994,116(4):812-823.
[12]Yan W,Komvopoulos K.Contact analysis of elastic-plastic fractal surfaces[J].Jounral of Applied Physics,1998,84(7):3617-3624.
[13]Liou J L.The theoretical study for microcontact model with variable topography parameters[D].China,Taiwan:National Cheng Kung University,2006.
[14]Zhang Xueliang,Wang Nanshan,Lan Guosheng,et al.Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations[J].Journal of Tribology,2014,136(1):011704-1-011704-10.
[15]张蓉竹,蔡邦维.功率谱密度的数值计算方法[J].强激光与粒子束,2000(12):661-664.
Zhang Rongzhu,Cai Bangwei.Numerical method of the power spectral density[J].High Power Laser and Particle Beams,2000(12):661-664.(in Chinese)
[16]张松,艾兴.HSK主轴/刀具联接的有限元分析[J].机械科学与技术,2004,23(6):631-633.
Zhang Song,Ai Xing.Finite element analysis of HSK spindle/toolholder interface[J].Mechanical Science and Technology,2004,23(6):631-633.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.006
* 国家科技重大专项资助项目(51375025);国家自然科学基金资助项目(3132004)
2015-06-10;
2015-08-22
TH131
赵永胜,男,1975年11月生,博士、副教授。主要研究方向为机床动力学、非线性系统辨识、系统仿真与控制。曾发表《Surface fractal topography-based contact stiffness determination of spindle-toolholder joint》(《Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science》 2016,Vol.230,No.4)等论文。 E-mail:yszhao@bjut.edu.cn

