变分模态分解在转子故障诊断中的应用*

向 玲,张力佳

(华北电力大学机械工程系 保定，071003)

变分模态分解在转子故障诊断中的应用*

向 玲,张力佳

(华北电力大学机械工程系 保定，071003)

针对转子故障诊断问题，提出一种基于变分模态分解(variational mode decomposition，简称VMD)的信号处理方法。该方法在获取分解分量的过程中通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽，从而能够自适应地实现信号的频域剖分及各分量的有效分离，对各单分量信号进行希尔伯特变换，即可得到瞬时的频率和幅值信息。对仿真信号和典型转子故障信号进行VMD方法和经验模态分解(empirical mode decomposition,简称EMD)方法的分析比较，以验证所提方法的有效性。仿真信号的分解结果表明，变分模态能够准确分离出信号中的固有模态分量且不存在模态混叠；转子故障实验信号的分析结果表明，所提方法能够有效提取出明显的故障特征，从而准确诊断出转子存在的故障。

变分模态分解； 转子故障； 故障特征； 时频分析

引 言

转子故障诊断的方法有多种，将时域和频域相结合反映信号全局特征的时频分析是一种重要的非线性、非平稳信号的处理方法。常用的时频分析方法如希尔伯特黄变换[1-2](Hilbert-Huang transform,简称HHT)能够在时频域中清晰展示出信号中的故障特征，从而有效进行故障诊断。HHT由EMD和希尔伯特变换(Hilbert transform,简称HT)组成，即对一个采集到的信号采用EMD进行分解，得到有限固有模态函数(intrinsic mode function,简称IMF)，然后使用HT对各分量进行解调，得到原始信号的时频信息。HHT时频分析方法在近几年的机械故障诊断中得到了有效应用[3-7]，但是EMD分解过程中的模态混叠现象影响了后续的时频分析[8-9]。VMD[10]是一种新的自适应信号预处理方法，分解过程实质是变分问题的迭代求解，可分为变分模型的建立和求解，是建立在Wiener滤波、Hilbert变换和外差解调等理论基础上的自适应信号分解方法[11-13]，对其分解得到的单分量进行Hilbert变换即可得到时频图。

笔者提出基于变分模态分解的转子故障信号时频分析方法，对仿真信号和转子故障实验信号进行了基于EMD方法与VMD方法的对比。结果表明，VMD方法能更准确地分离出转子故障信号分量，且故障特征值明显，可有效诊断出转子的故障。

1 变分模态分解原理

1.1 变分模型的建立

假设输入信号x(t)是由有限个中心频率不同、带宽有限的分量组成，将信号分解问题转换到变分模型中进行分解。在各分量之和等于原始输入信号x(t)约束下，寻求各分量的聚集带宽之和最小。构造步骤如下[10]。

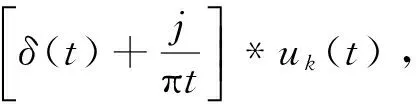
3) 计算解调信号梯度的平方L2范数，估计出模态信号带宽。受约束的最优化变分模型为

(1)

1.2 变分模型的求解

使用二次惩罚因子α和拉格朗日乘法算子λ(t)，将约束性问题变为非约束性问题。二次惩罚因子可以保证含高斯噪声的情况下信号的重构精度，拉格朗日乘子可以保证约束条件的严格性。扩展的拉格朗日函数表达式为

(2)

(3)

利用Parseval/Plancherel傅里叶等距离变换，将式(3)变换到频域，得到各模态的频域更新

（3）另取0.1 mol/L的氢氧化钠溶液2mL，滴加2滴1%的酚酞溶液，用水稀释至20mL，将0.1 mol/L的盐酸改为0.01 mol/L的稀盐酸重复上述实验操作，直至溶液的pH为2.00为止，用蒸馏水冲洗pH电极。

(4)

根据同样计算过程，将中心频率取值问题转换到频域，得到中心频率的更新

(5)

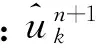
1.3 VMD算法具体过程

VMD算法具体步骤[13]如下：

2) 根据式(4)，(5)，更新uk和ωk；

3) 更新λ为

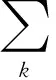
2 时频谱与边际谱

(6)

构造解析信号，得到幅值和相位函数为

瞬时频率为

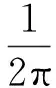
(9)

(10)

其中：Re表示取实部并忽略残余项；ak(t)为解析信号的瞬时幅值；ωk(t)为解析信号的瞬时频率。

式(10)描述了信号中每个时刻包含的频率成分，据此可作出Hilbert时频谱[14]。

进一步定义边际谱为

(11)

边际谱的幅值能准确反映原始信号中某频率分量是否真实存在，表示信号在某频率下的时间段内的幅值之和[15]。

3 仿真信号分析

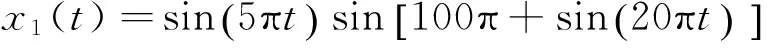
图1 仿真信号时域图Fig.1 Time domain of simulation signal

利用EMD方法对仿真信号进行分解，得到的分量时域图如图2所示,从上到下依次为IMF1，IMF2，IMF3，IMF4，IMF5。EMD分解受仿真信号中随机噪声信号的影响，分解得到的信号分量存在明显的模态混叠现象。

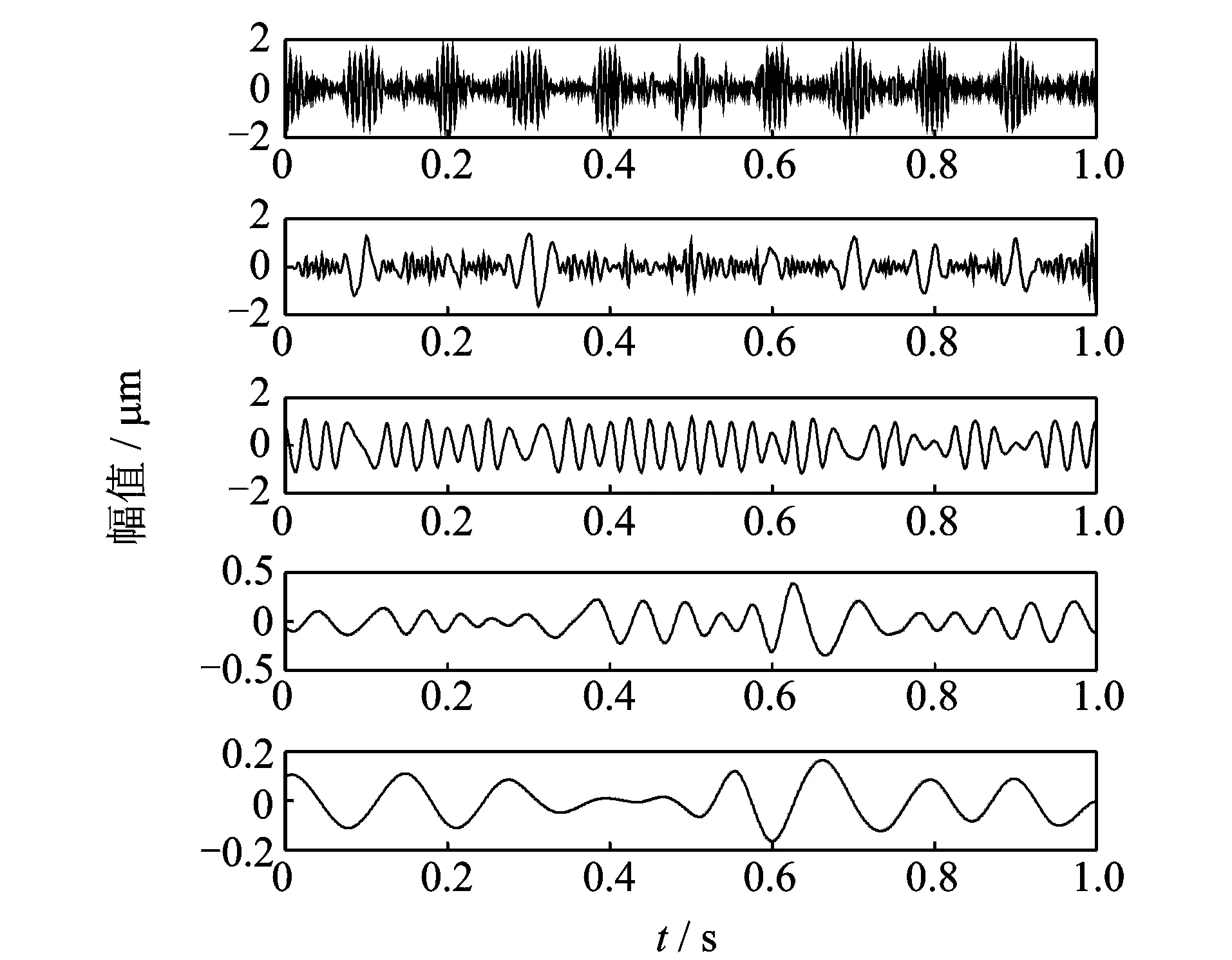
图2 仿真信号的EMD分解结果Fig.2 EMD result generated from the simulation signal

VMD分解与EMD分解的最大不同在于VMD需要提前设置所需处理信号的分解个数k。若k值偏大，会导致分解结果出现过分解；若k值偏小，则会出现欠分解，因此合理设置k值是使用VMD的关键。笔者采用中心频率相近原则[16]来选择k值，同时，惩罚因子α采用默认值2 000。不同k值时对仿真信号进行分解，并计算各模态分量的中心频率，如表1所示。由表1可知，当k=4时出现了频率中心相近的模态分量，即出现了过分解。因此，使用VMD对仿真信号进行3层分解，得到的各分量时域图如图3所示，从上到下依次为F1，F2，F3。图3中，F1，F2分量分别对应仿真信号中的正弦信号与调幅调频信号，信号分量时域图规律清晰，不存在模态混叠现象；F3分量为仿真信号中的随机噪声信号。通过对比EMD，VMD两种方法对仿真信号的分解，表明VMD能够准确将仿真信号中的不同模态分量分离。

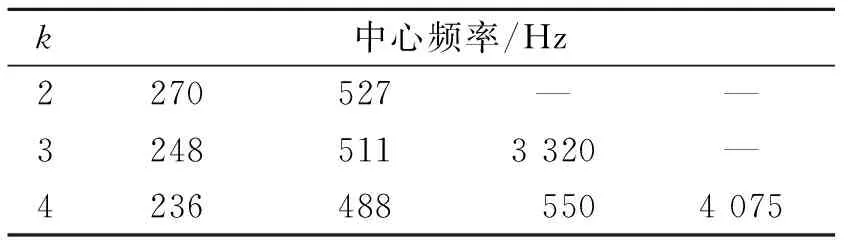
表1 不同k值各模态分量的中心频率Tab.1 Center frequency corresponding to different k

图3 仿真信号的VMD分解结果Fig.3 VMD result generated from the simulation signal

4 实验故障信号分析

使用Bebntly RK-4转子实验台模拟转子不平衡、碰摩、油膜涡动等典型故障。故障信号的记录设备采用美国Iotech公司的ZonicBook/618E。

4.1 转子不平衡故障分析

加载不平衡质量1 g在转子圆盘45°角处进行转子不平衡实验。调整转子的转速为2 480 r/min，模拟转子不平衡故障。采样频率为1 280 Hz，选取记录数据中的1 024点进行分析。

图4为转子不平衡故障信号的时域图和频谱图。由图4(a)可知，转子不平衡故障信号的时域波形呈现正弦波形。在频谱图4(b)中，41.33 Hz基频幅值明显突出，有二倍频等高频分量出现,但幅值较小，不能通过频谱图判断出是否有转子故障发生。

图4 转子不平衡故障信号的时域图和频谱图Fig.4 Time domain and spectral diagram of rotor imbalance signal

图5 转子不平衡信号的时频图Fig.5 Time-frequency spectrum of rotor imbalance signal

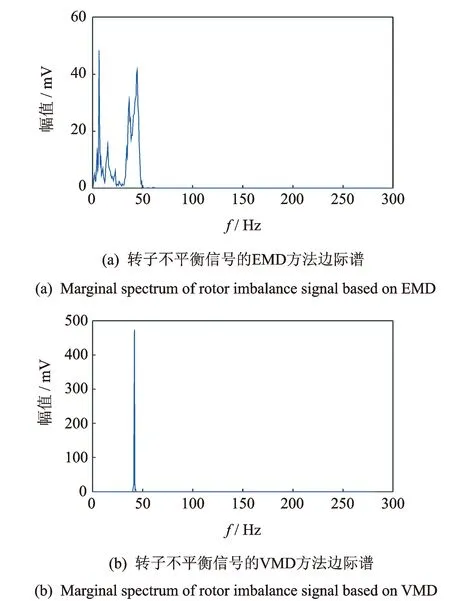
图6 转子不平衡信号的边际谱Fig.6 Marginal spectrum of rotor imbalance signal

图5(a)为基于EMD方法的转子不平衡故障信号时频分析图。图中可辨识出转子不平衡故障特征频率为41.33 Hz，但故障特征频率的调频现象明显，且在0.6～0.8 s存在模态混叠。根据中心频率相近原则，转子不平衡故障信号选择k值为4进行VMD分解分析，得到的时频图如图5(b)所示。图中不平衡故障特征频率41.33 Hz清晰可见，且不存在模态混叠现象。图6为两种方法得到的边际谱。结果表明，VMD能够准确分离出原始信号中的不平衡故障信号分量，且故障特征的幅值明显突出。在转子不平衡故障信号的时频分析中，基于VMD方法的时频图中故障特征频率清晰明显，可有效诊断出转子不平衡故障。

4.2 转子碰摩故障分析

转子局部碰摩实验时转子转速为1 260 r/min，用碰摩针与转轴进行局部碰摩故障实验。采样频率设置为1 280 Hz，选取记录数据中的1 024点进行分析。图7为转子局部碰摩故障信号的时域图和频谱图。由图7(a)可看出，转子局部碰摩时域图为规则正弦，在7(b)中，21 Hz基频分量及2倍频42 Hz幅值明显，其他高倍频分量幅值较小且不易辨识，简单的频谱分析不能有效判断出转子故障。

图7 转子局部碰摩信号的时域和频谱图Fig.7 Time domain and spectral diagram of local rotor rubbing signal

图8 转子局部碰摩信号的时频图Fig.8 Time-frequency spectrum of rotor rubbing fault signal

图9 转子碰摩故障信号的边际谱Fig.9 Marginal spectrum of local rotor rubbing fault signal

图8(a)为基于EMD方法的转子碰摩故障信号时频分析图，可辨识出转子碰摩故障特征频率21 Hz及不稳定的倍频成分。根据中心频率相近原则，转子碰摩故障信号选择k值为5进行VMD分解分析，得到的时频图如图8(b)所示。图中碰摩故障特征频率21 Hz及2倍频42 Hz清晰明显，不存在模态的混叠。进一步对比两种方法得到的边际谱图9(a),(b)可知，VMD准确分离出原始信号中的转子碰摩故障信号分量，且故障特征频率的幅值明显突出。基于VMD分解的时频分析方法提取出的碰摩故障特征明显，可有效判断出转子局部碰摩故障。

4.3 转子油膜涡动故障分析

转子产生油膜涡动故障时，理论上会产生频率值为转子转频0.43～0.48倍的故障特征频率。通过转子实验平台的调速电机控制器，使转子转速达到2 800 r/min，转子产生动力失稳从而模拟油膜涡动故障。采样频率设为1 280 Hz，选取数据中的1 024点进行分析。

图10为转子油膜涡动故障信号的时域图和频谱图。由图10(a)可知，时域图为规则信号的波动，在频谱图10(b)中，幅值最大的频率分量为半频24 Hz，基频46.67 Hz幅值也有明显突出，同时还出现了幅值不明显的高倍频分量，依靠单一频谱图分析无法准确判断出转子是否发生油膜涡动故障。

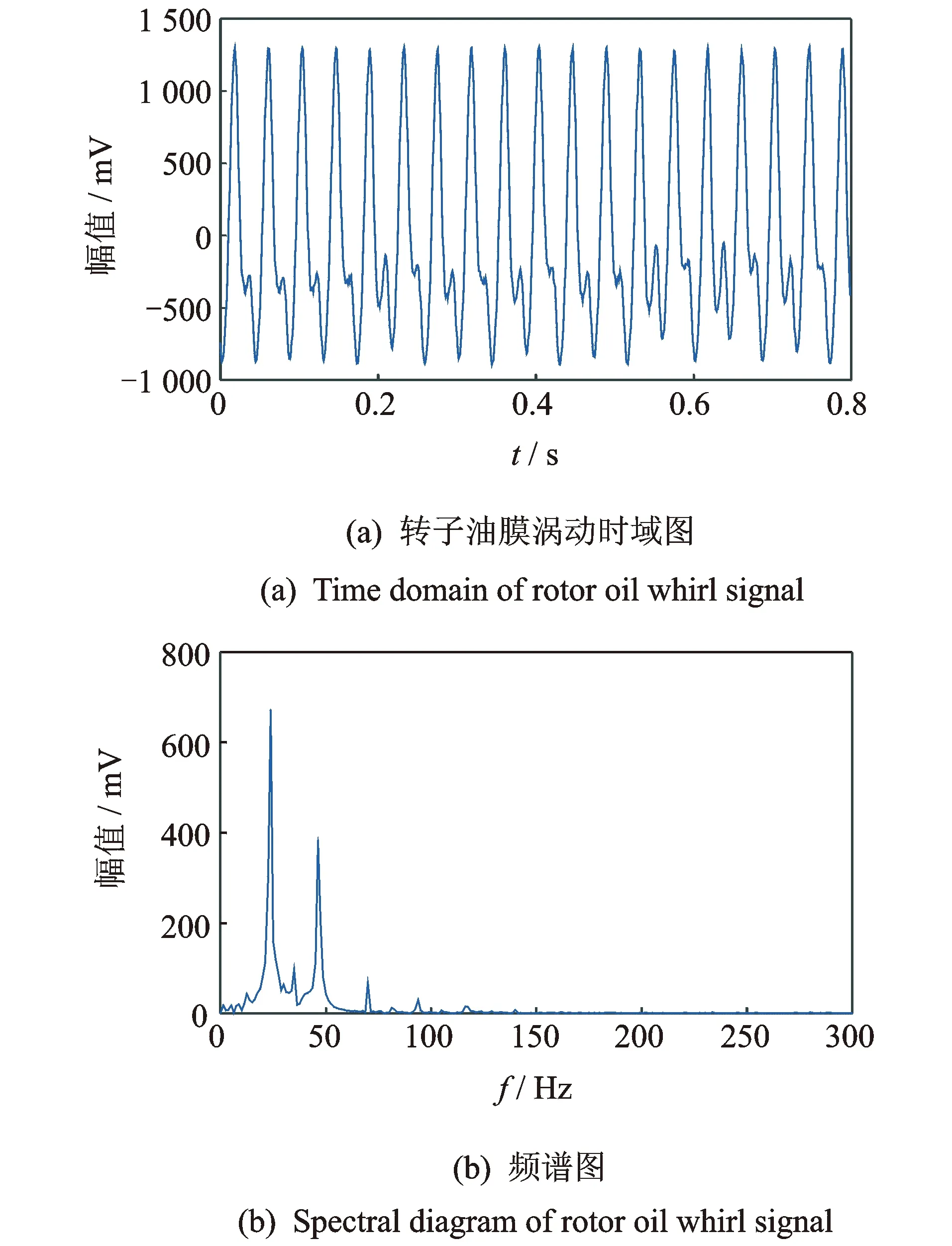
图10 转子油膜涡动故障信号的时域图和频谱图Fig.10 Time domain and spectral diagram of rotor oil whirl signal

图11 转子油膜涡动信号的时频图Fig.11 Time-frequency spectrum of rotor oil whirl signal

图11(a)为基于EMD方法得到的转子油膜涡动故障信号时频分析图。图中可以辨识出转子油膜涡动的故障特征频率24 Hz，但是0.4～0.6 s有明显的模态混叠。根据中心频率相近原则，转子油膜涡动故障信号选择k值为4进行VMD分解分析，得到的时频图如图11(b)所示。图中可以有效辨识出转子基频46.67 Hz与油膜涡动故障的特征频率24 Hz，且不存在模态混叠。12(a)，(b)为通过两种方法得到的边际谱图。结果表明，VMD可准确分离出原始信号中的故障分量信号，且故障特征的幅值明显突出，不存在模态混叠。基于VMD方法的时频分析得到的故障特征清晰明显，油膜涡动故障特征频率提取效果优于基于EMD方法的时频分析，故障诊断效果可得到提高。

图12 转子不平衡信号的边际谱Fig.12 Marginal spectrum of rotor oil whirl signal

5 结束语

提出一种基于变分模态分解的转子故障信号时频分析方法，针对仿真信号与转子实验故障信号对比分析了EMD和VMD方法的有效性。仿真信号的分解结果表明，EMD分解得到的分量信号存在模态混叠现象，VMD方法分解得到的分量信号与仿真信号中存在的分量信号一致。转子典型故障信号的分析结果表明，基于VMD的时频分析方法能够有效避免出现模态混叠，提取出的故障特征清晰明显，可准确诊断出转子存在的故障。这为转子故障的有效诊断提供了一种新的时频分析方法。

[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A，1998,454:903-995.

[2] Huang N E,Shen Z,Long S R,et al.A new view of nonlinear water waves:the Hilbert spectrum[J].Annual Review of Fluid Mechanics,1999,31:417-457.

[3] Yang Zhensheng,Yu Zhonghua,Chao Xie,et al.Application of Hilbert-Huang transform to acoustic emission signal for burn feature extraction in surface grinding process[J].Measurement,2014,47:14-21.

[4] 郑近德，程军圣.改进的希尔伯特-黄变换及其在滚动轴承故障诊断中的应用[J].机械工程学报,2015,51(1):138-145.

Zheng Jinde,Cheng Junsheng.Improved Hilbert-Huang transform and its applications to rolling bearing fault diagnosis[J].Journal of Mechanical Engineering,2015,51(1):138-145.(in Chinese)

[5] 马文朋，张俊红，马梁，等.改进的经验模式分解在机械故障诊断中的应用[J].振动、测试与诊断,2015,35(4):637-644.

Ma Wenpeng,Zhang Junhong,Ma Liang,et al.Applications of improved empirical mode decomposition in machinery diagnosis[J].Journal of Vibration,Measurement &Diagnosis,2015,35(4):637-644.(in Chinese)

[6] 熊炘，杨世锡，甘春标.运用BF-HHT的转子径向碰摩故障特征提取方法[J].振动、测试与诊断,2012,32(2):192-196.

Xiong Xin,Yang Shixi,Gan Chunbiao.Fault feature extraction method for rotor system under radial impact based on BE-HHT[J].Journal of Vibration,Measurement &Diagnosis,2012,32(2):192-196.(in Chinese)

[7] 孟宗，李姗姗.基于小波改进阈值去噪和HHT的滚动轴承故障诊断[J].振动与冲击,2013,32(14):204-208.

Meng Zong,Li Shanshan.Rolling bearing fault diagnosis based on improved wavelet threshold de-noising method and HHT[J].Journal of Vibration and Shock,2013,32(14):204-208.(in Chinese)

[8] 曹莹，段玉波，刘继承.Hilbert-Huang变换中的模态混叠问题[J].振动、测试与诊断,2016,36(3):518-523.

Cao Ying,Duan Yubo,Liu Jicheng.Research and application of mode-mixing in Hilbert-Huang transform[J].Journal of Vibration,Measurement &Diagnosis,2016,36(3):518-523.(in Chinese)

[9] 向玲，鄢小安.汽轮机转子故障诊断中LMD法和EMD法的性能对比研究[J].动力工程学报,2014,34(12):945-951.

Xiang Ling,Yan Xiaoan.Performance contrast between LMD and EMD in fault diagnosis of turbine rotors[J].Journal of Chinese Society of Power Engineering,2014,34(12):945-951.(in Chinese)

[10]Dragomiretskiy K,Zosso D． Variational mode decomposition[J].Transactions on Signal Processing,2014,62(3):531-544．

[11]Aneesh C,Sachin K,Hisham P M,et al.Performance comparison of variational mode decomposition over empirical wavelet transform for the classification of power quality disturbances using support vector machine[J].Procedia Computer Science,2015(46):372-380.

[12]Salim L.Comparative study of signal denoising by wavelet threshold in empirical and variational mode decomposition domains[J].Healthcare Technology Letters,2014,1(3):104-109.

[13]刘长良，武英杰，甄成刚.基于变分模态分解和模糊C聚类均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):3358-3365.

Liu Changliang,Wu Yingjie,Zhen Chenggang.Rolling bearing fault diagnosis based on variational mode decomposition and fuzzy C means clustering[J].Proceedings of the CSEE,2015,35(13):3358-3365.(in Chinese)

[14]张帅，杨勇，韩清凯，等.基于HHT的转子系统定点碰摩实验研究[J].振动与冲击,2010,29(7):121-125.

Zhang Shuai,Yang Yong,Han Qingkai,et al.Experimental study on a rotor system with rub-impact at fixed limiter based on HHT[J].Journal of Vibration and Shock,2010,29(7):121-125.(in Chinese)

[15]马百雪，潘宏侠，杨素梅.基于改进的HHT边际谱齿轮箱故障诊断[J].煤矿机械,2013,34(10):251-254.

Ma Baixue,Pan Hongxia,Yang Sumei.Gearbox fault diagnosis based on improved Hilbert-Huang transform marginal spectrum[J].Coal Mine Machinery,2013,34(10):251-254.(in Chinese)

[16]马增强，李亚超，刘政，等.基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J].振动与冲击,2016,35(13):134-139.

Ma Zengqiang,Li Yachao,Liu Zheng,et al.Rolling bearings′ fault feature extraction based on variational mode decomposition and Teager energy operator[J].Journal of Vibration and Shock,2016,35(13):134-139.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.025

* 国家自然科学基金资助项目(51675178，51475164)

2016-06-24；

2016-08-08

TH165.3； TK288

向玲，女，1971年4月生，博士、教授。主要研究方向为非线性动力学和故障诊断。曾发表《汽轮发电机组轴系扭振的时频特征分析》(《动力工程学报》2011年第31卷第9期)等论文。E-mail:xiangling5042@126.com