利用磁记忆信号特征参数表征拉伸应力状态*

易术春，王 威，苏三庆，徐 秦，曾发荣

(西安建筑科技大学土木工程学院 西安,710055)

利用磁记忆信号特征参数表征拉伸应力状态*

易术春，王 威，苏三庆，徐 秦，曾发荣

(西安建筑科技大学土木工程学院 西安,710055)

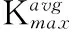
金属磁记忆； 量化关系； 特征参量； 损伤程度

引 言

铁磁构件由于其具有轻质高强、材质均匀、制作简单、韧性好和耐高压等特点，被广泛应用于机械和建筑领域。但这些构件的受力和构造复杂，在服役过程中遭受长期循环载荷、自然灾害以及人为因素的影响，不可避免地产生一些隐性损伤，威胁整个设备和结构的正常使用和安全。常规的无损检测技术(超声波法、射线法和涡流检测方法等)只能检测出已经成形的宏观缺陷，无法对早期的隐性损伤进行检测[1-3]。金属磁记忆检测技术是一种新兴的无损检测方法，能够对构件的应力集中和早期损伤进行诊断，防止突发性失效，是迄今为止对铁磁构件进行早期诊断唯一有效的无损检测方法[4]。该方法的原理是铁磁构件受工作载荷和地球磁场的共同作用，在应力和变形集中区发生具有磁致伸缩性质的磁畴组织定向的和不可逆的重新取向，进而导致漏磁场Hp的变化，即切线分量具有最大值，法向分量改变符号且过零点[5-6]。通过检测铁磁构件表面的漏磁场分布情况，可对应力集中或缺陷进行准确判断[7-8]。

由于金属磁记忆检测技术操作简单方便且不需要对被测构件进行清理、人工磁化以及贴附传感器等，因此广泛应用于石油、化工和机械等领域的检测。近年来，对漏磁信号与应力状态之间的关系展开了大量研究。文献[9]研究了应力状态、微观缺陷长度及扫描路径对漏磁信号的影响。文献[10]研究了20钢V型缺陷平板在拉伸载荷下应力磁化的反转效应。文献[11]研究了带圆孔平板试件在静拉应力作用下应力集中区磁信号和磁畴组织的变化规律。这些研究均未能建立磁记忆信号与应力之间的定量关系。

笔者通过对Q345B钢试件进行静载拉伸试验，采集规定路径上的法向漏磁场值，得到了不同应力状态下的磁记忆信号变化规律，研究了试件断裂处的法向分量Hp(y)值和特征参量随应力的变化，并建立磁场梯度指数与应力的量化关系，利用磁记忆信号表征试件应力状态。

1 试验材料与方法

1.1 试验材料

试验材料为常用的Q345B钢，其力学性能和化学组成如表1和表2所示。

表1 Q345低碳钢力学性能Tab.1 Mechanical properties of Q345 low carbon steel

表2 Q345低碳钢化学组成Tab.2 Chemical composition of Q345 low carbon steel

利用线切割机将试件尺寸加工为200 mm×50 mm×10 mm。考虑到实际应用情况,未对试件进行退磁。试验前在试件正面测量范围内画好检测线,检测线长度为80 mm，如图1所示。

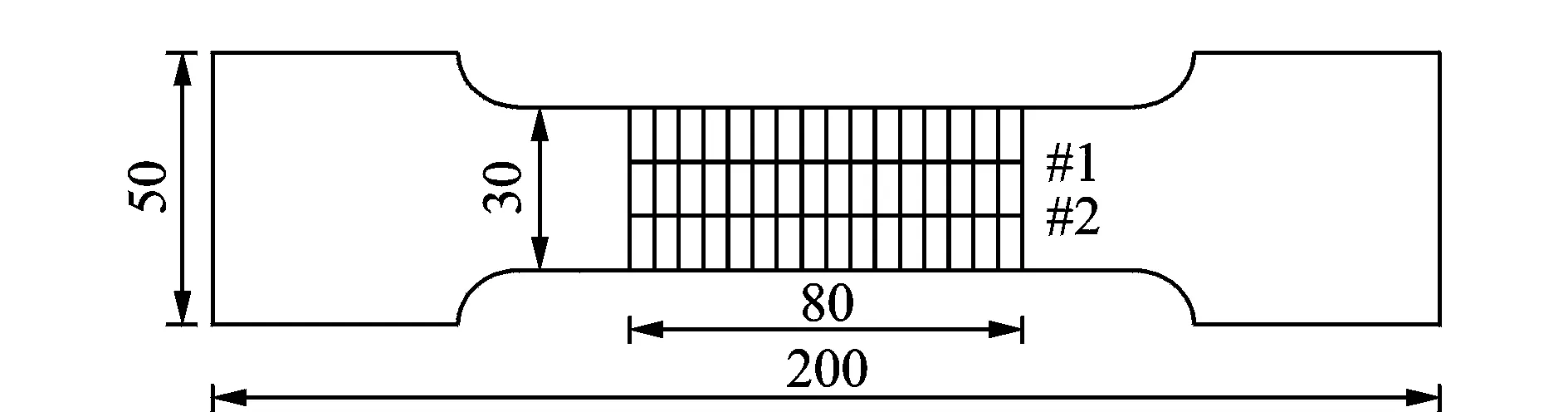
图1 试件尺寸及检测线位置(单位:mm)Fig.1 Size of specimen and the arrangement of measured lines (unit:mm)

1.2 试验设备及方法

拉伸试验在WAW-2 000D电液伺服万能试验机上进行，其主要技术参数：最大试验力为2 000 kN，试验力示值相对误差≤±1%，试验力测量范围为最大试验力的2%～100%，如图2所示。磁记忆信号检测设备选用高精度的WT10B型数字高斯计，其基本误差为±2%，精度为0.01 mT。

图2 WAW-2 000D试验机Fig.2 WAW-2 000D testing machine

试验开始前，预先对试件进行静载拉伸，得到力-位移关系曲线，如图3所示。由曲线可知，试件加载到96 kN时发生屈服，加载到120 kN时出现明显的颈缩现象。为了更好地观察试件从弹性阶段过渡到塑性阶段过程中磁记忆信号的变化特征，采取分级加载方式，并在屈服强度处进行细化，试件的加载等级为0，40，70，80，90，96，100，110和120 kN。在试验过程中，当载荷达到预先设定值后，静置一段时间，然后采用磁记忆检测仪进行在线检测。测量前，将检测设备初始化，将初始值校正到0.05 mT≈40 A/m。由于磁场是矢量场，位置及环境的改变会对磁信号产生很大影响，所以本试验均是在同一位置和同一环境下进行。检测时，沿着检测线从左至右逐点依次检测，检测步距为5 mm。根据文献[12]，将传感器直接贴着试件表面进行磁信号采集是消除提离效应的好方法。因此，测量时将传感器垂直并紧贴试件表面，保证在检测过程中提离值保持为零，且每个检测点至少检测3次，直至信号稳定，以减小误差。

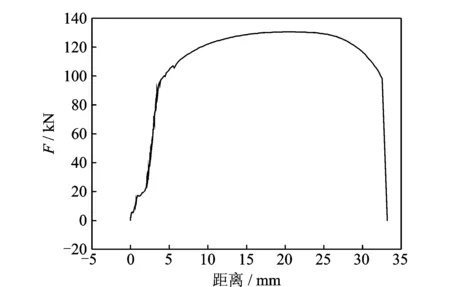
图3 试件的力-位移曲线Fig.3 Force vs.displacement curve of specimen

2 试验结果

2.1 不同载荷对磁记忆信号的影响

加载完成后，对4组试验数据进行整理，发现4组试件重复试验中检测线的磁信号有相同的变化趋势，尤其同一试件的两条测量线上法向分量值表现出很强的相似性。为减小检测误差，检测结果取两条检测线上法向分量的平均值，并选取其中一个试件作为研究对象。

图4为弹性阶段和塑性阶段试件表面法向分量分布曲线。初始阶段，试件表面具有较大的磁信号，主要是因为在试件制作过程中磁畴组织发生了重新排列。弹性阶段，试件的磁信号与初始磁信号有很大差异，磁信号曲线出现过零点现象，沿加载方向近似为斜直线且保持稳定，并随着应力的增大而增加。这表明在应力和地磁场共同作用下，试件内部产生了很高的应力能。根据物质结构实际存在状态必是能量最小状态的原则，为了使总的自由能趋于最小，在试件内部的位错聚集处磁畴壁必将发生不可逆的重新取向。同时，由于金属的多种内耗效应，试件内部将出现不同程度的磁化，且钢材在制造过程中其内部本身就有杂质和缺陷，而这些杂质和缺陷会导致材料局部的磁导率下降，形成高磁阻区，阻碍磁力线的通过，在这些缺陷区域内形成不均匀的磁势差，使原本均匀的磁力线出现畸变，从而在试件表面产生不等的自有漏磁场[13-14]。随着应力的增大，试件内部逐渐达到磁饱和状态，磁信号的分布趋于稳定。屈服阶段，磁信号曲线出现非线性变化，斜率由负变为正，相对于弹性阶段磁信号发生了反转现象，且Hp(y)变化幅度相对于弹性阶段出现了明显降低。这是由于塑性变形加速了位错密度的积累，位错对磁畴的钉扎作用阻碍了磁畴的有序化运动，并降低了磁化强度。

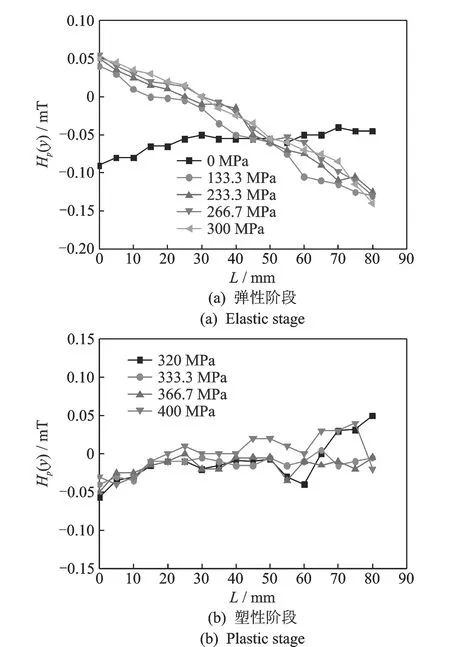
图4 不同拉伸载荷下Hp(y)值的变化Fig.4 Variations of Hp(y) values under different tensile loads

2.2 应力σ与磁记忆信号特征参数之间的关系

1) 根据磁偶极子模型，自由漏磁场反映的是磁荷密度的积分场。为了更好的建立应力σ与磁信号之间的量化关系，采用基于离散数据的中心差分算法对磁信号法向分量进行一阶微分

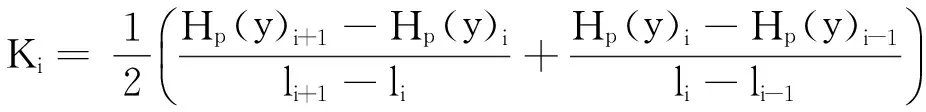
(1)

其中：Ki为第i个检测点的法向分量梯度值，反映了磁信号变化的快慢程度；Hp(y)i和li分别为第i个检测点的法向分量值和位置坐标。

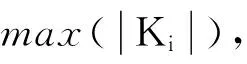
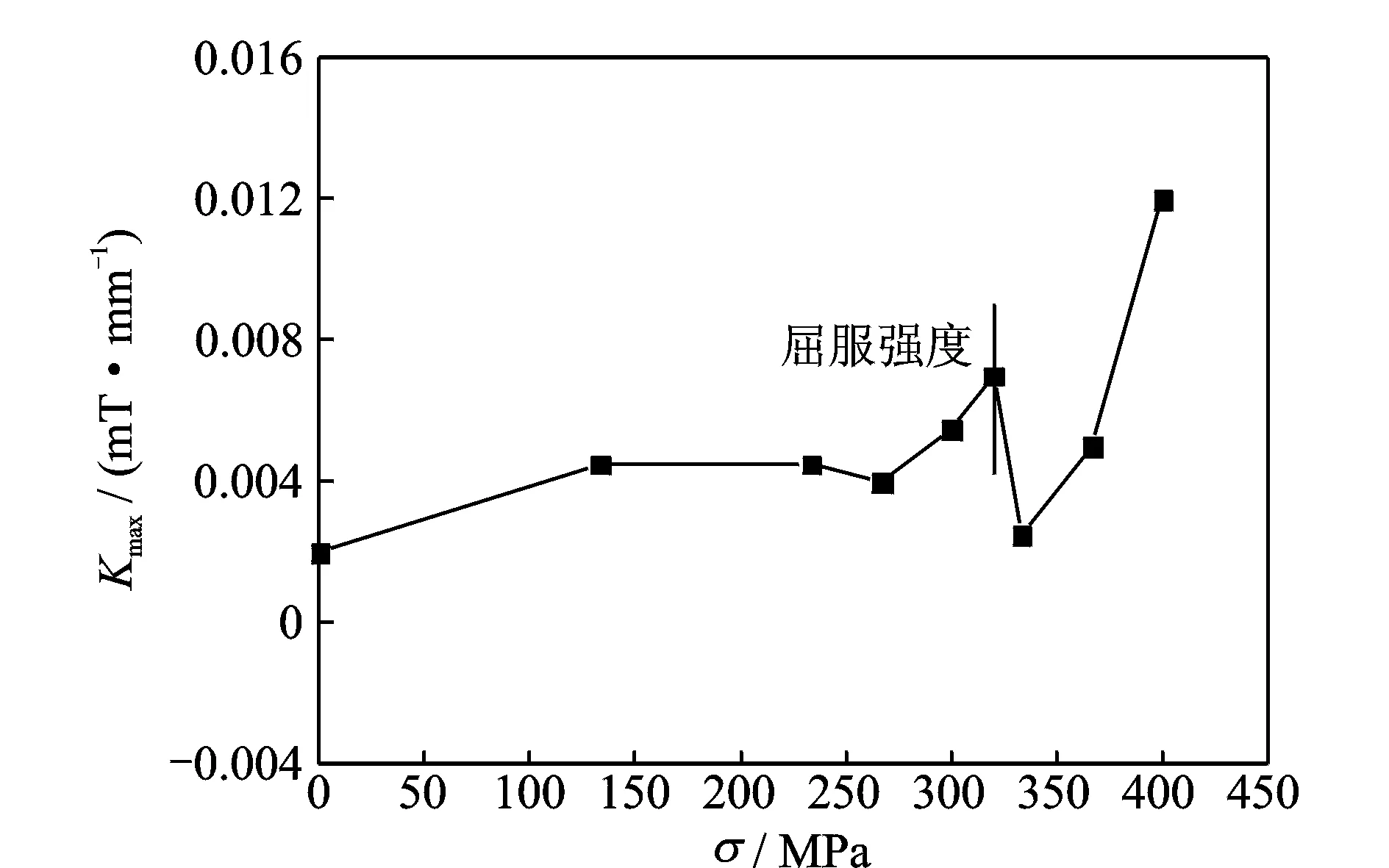
图5 应力σ与梯度Kmax之间的关系曲线Fig.5 Relationship between stress σ and gradient Kmax

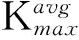
(2)

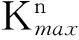
图6 应力σ与梯度之间的关系曲线Fig.6 Relationship between stress σ and gradient

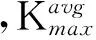
图7 应力σ与断裂处Hp(y)之间的关系曲线Fig.7 Relationship between stress σ and Hp(y) at the fracture position

3) 试件的最终断裂位置为检测线L=45 mm处。为研究钢结构易损部位的磁记忆信号变化特征，建立了试件断裂处磁场法向分量Hp(y)与应力σ的关系曲线，如图7所示。Hp(y)随着应力σ的增加而增大，并在屈服强度处出现跳变。在加载初期，Hp(y)变化幅度很小，主要是由于此时应力小，试件内部没有出现应力集中。当应力增加至屈服极限时，试件内部发生应力集中，出现滑移和位错，并且导致试件产生微裂纹，磁记忆信号出现突然地跳变。当应力增加到试件出现明显的颈缩现象时，随着裂纹的增多及相互交错，法向分量急剧增大，此时试件濒临破坏。可见，断裂处Hp(y)值能很好地反映试件断裂处的损伤程度，为钢结构易损部位的量化提供依据。

y=Aexp(R0x)+y0

(3)

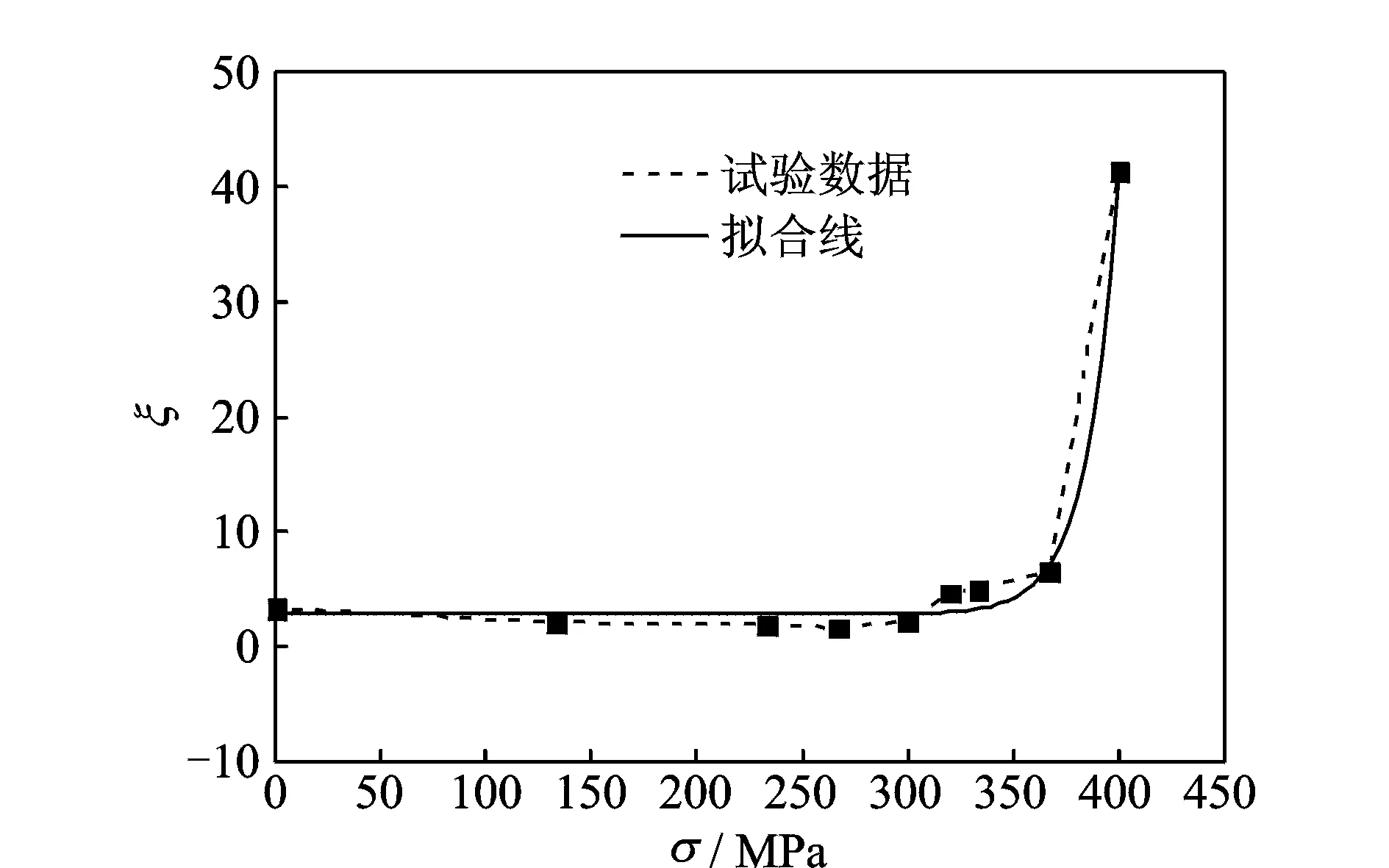
图8 应力σ与磁场梯度指数ξ之间的关系曲线Fig.8 Relationship between stress σ and magnetic field gradient index ξ

得到γ值与应力σ之间的量化关系

ξ=Aexp(R0σ)+ξ0

(4)

其中：A=1.21×10-10；R0=0.066 MPa-1；ξo=2.85；拟合度为99.1%。

结果表明，ξ值可以准确表征试件的应力状态并对构件的失效进行预警。

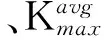
3 分析及讨论

3.1 磁信号反转分析

文献[15]中，根据Jiles-Atherton模型，单轴应力可以通过磁致伸缩改变试件内部的有效场，相当于附加了一个应力场，这个应力场为

(5)

其中：λ为磁致伸缩系数；μ0为真空磁导率；M为磁化强度；θ为应力与磁场强度之间的夹角；ν为泊松比。

本试验中，Q345B钢的泊松比ν=0.3，θ=46°，则有效磁场Heff为

(6)

试件的磁致伸缩系数λ可由经验模拟

(7)

利用文献[16]可知

γ1(0)=7×10-18m2/A2

γ2(0)=-3.3×10-30m2/A4

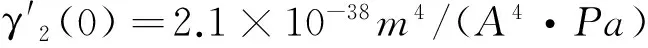
在本试验中，地磁场强度H=40 A/m，Q345B钢按线性物质考虑，假定其磁化率为210，内磁畴耦合系数α=0.001，真空磁导率μ0=4π×10-7H/m。屈服后的磁信号发生反转现象，说明Heff<0

(8)

将各参数值带入式(8)，当拉应力大于308.6 MPa和压应力大于238.7 MPa时，均会导致磁信号发生发转现象，与本试验结果一致。因此，图4中磁信号Hp(y)的反转现象可用Jiles-Atherton模型解释。

3.2 断裂处法向分量分析

试验结束后观察到，横截面积的变化主要发生在关于试件断裂处对称的区域内。假定这个区域A为无限小，并且在拉应力作用下只在区域交界处横截面积发生变化，而区域内和区域外的横截面积保持不变，如图9所示。

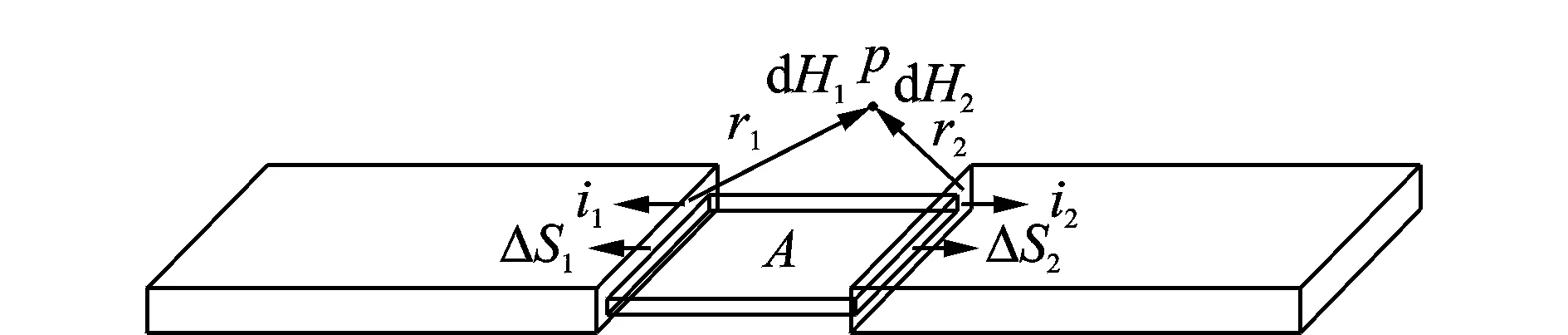
图9 感应磁场分布模型Fig.9 Model of inductive magnetic field

设试件垂直于地磁场H的横截面积为S，在应力作用下经过时间Δt后，横截面积变化了ΔS，则交界面处感应电动势为

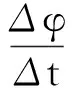
(9)

其中：μr为材料相对磁导率；μ0为真空磁导率。

由式(9)可知，电动势E正比于ΔS。在电动势的作用下，交界面处将产生感应电流i，且i正比于感应电动势，因此感应电流i也正比于ΔS。

根据比奥-萨伐尔定律可知，在电流i作用下，试件表面某点P处的磁场强度为

(10)

由式(10)可知，试件表面的磁场强度正比于电流i，因此磁场强度也正比于ΔS。

根据钢材的本构关系，应力的作用必然导致试件产生纵向应变，且应变随着应力的增加而增大。由泊松比的定义可知,横向应变与纵向应变呈正比关系，横截面积的改变量ΔS和试件断裂处的磁场强度H随着应力的增加而增大，故图7中的磁信号随应力增加而增大的现象可由式(10)定性分析。

此外，式(10)还可解释磁信号随着提离值的增大而减弱的原因。由式(10)可知，磁场强度H与测量半径r呈反比，即提离值越大时，检测到的磁场强度越小，这一现象在文献[17]已经证实。

4 结 论

1) 弹性阶段的磁信号曲线沿加载方向近似为斜直线且保持稳定，随着应力的增加而增大；屈服阶段的磁信号曲线出现非线性变化，相对于弹性阶段磁信号发生了反转现象。Jiles-Atherton模型可解释磁信号发生反转的原因。

2) 分析了磁信号特征参量Kmax随应力的变化特征，当试件达到屈服极限时，磁信号特征参量Kmax出现极大值，可以提取Kmax的极大值作为特征量，对试件是否进入塑性阶段进行判定。

4) 建立了磁场梯度指数ξ与应力σ的量化关系，ξ值可表征试件的应力状态，为金属磁记忆检测技术定量评估和安全预警提供理论和试验依据。

[1] Yang Lijian,Liu Bin,Chen Lijia,et al.The quantitative interpretation by measurement using the magnetic memory method (MMM)-based on density functional theory[J].NDT&E International,2013,55:15-20.

[2] 张伟伟,武静,马宏伟.基于Lyapunov指数的超声导波检测技术[J].振动、测试与诊断,2015,35(2):250-257.

Zhang Weiwei,Wu Jing,Ma Hongwei.Ultrasonic guided wave inspection method based on lyapunov exponents[J].Journal of Vibration,Measurement &Diagnosis,2015,35(2):250-257.(in Chinese)

[3] 胥永刚,冯明时,马海龙,等.微弱信号的差分振子检测方法[J].振动、测试与诊断,2013,33(2):224-230.

Xu Yonggang,Feng Mingshi,Ma Hailong,et al.Method of weak signal detection based on differential oscillator[J].Journal of Vibration,Measurement &Diagnosis,2013,33(2):224-230.(in Chinese)

[4] Doubov A A.Express method of quality control of a spot resistance welding with usage of metal magnetic memory[J].Welding in the World,2002,46:317-320.

[5] Ren Jilin,Pan Qianghua,Yang Sheng,et al.An experimental research of the effects of stress upon the magnetic domains in magnetic memory testing[J].International Journal of Applied Electromagnetics and Mechanics,2010,33:1143-1148.

[6] 胥永刚,谢志强,孟志鹏,等.基于奇异值分解的磁记忆信号特征提取方法[J].振动、测试与诊断,2014,34(6):1105-1109.

Xu Yonggang,Xie Zhiqiang,Meng Zhipeng,et al.Feature extraction method of magnetic memory signal based on SVD[J].Journal of Vibration,Measurement &Diagnosis,2014,34(6):1105-1109.(in Chinese)

[7] 王威,樊浩,苏三庆,等.钢结构对接焊缝隐性损伤的磁记忆检测试验研究[J].西安建筑科技大学学报:自然科学版,2014,46(4):497-501.

Wang Wei,Fan Hao,Su Sanqing,et al.Experimental detection on implicit damage of butt weld of steel structure by magnetic memory testing[J].Journal of Xi′an University of Architecture &Technology:Natural Science Edition,2014,46(4):497-501.(in Chinese)

[8] 董丽虹,徐滨士,王慧鹏,等.应力诱发铁磁材料预制切口产生的二维弱磁场信号特征研究[J].材料工程,2011(12):16-19.

Dong Lihong,Xu Binshi,Wang Huipeng,et al.Character of stress-induced two-dimensional low intensity field on precut notch zone of ferromagnetic material[J].Journal of Materials Engineering,2011(12):16-19.(in Chinese)

[9] 张辉,李龙军,杨宾峰,等.金属磁记忆定量化评价的三维仿真分析与实验[J].空军工程大学学报,2013,14(1):57-61.

Zhang Hui,Li Longjun,Yang Binfeng,et al.Dimensional finite element simulation and experimental study of metal magnetic memory quantitative evaluation[J].Journal of Air Force Engineering University,2013,14(1):57-61.(in Chinese)

[10]李一,任尚坤.铁磁试件静载拉伸时应力磁化的反转效应[J].钢铁研究学报,2013,25(3):30-33.

Li Yi,Ren Shangkun.Magnetization reversal of ferromagnetic specimen under the static tension conditions[J].Journal of Iron and Steel Research,2013,25(3):30-33.(in Chinese)

[11]方发胜,张利明,李新蕾,等.静拉应力作用下Q235钢磁记忆检测的试验研究[J].无损探伤,2013,37(3):7-10.

Fang Fasheng,Zhang Liming,Li Xinlei,et al.Experimental study of Q235 steel magnetic memory testing under the action of the static tensile stress[J].Nondestructive Test,2013,37(3):7-10.(in Chinese)

[12]Yao Kai,Deng Bo,Wang Zhengdao.Numerical studies to signal characteristics with the metal magnetic memory-effect in plastically deformed samples[J].NDT&E International,2012,47:7-17.

[13]任吉林,林俊明,池永滨,等.金属磁记忆检测技术[M].北京:中国电力出版社,2000:12-13.

[14]Yao Kai,Wang Zhengdao,Deng Bo,et al.Experimental research on metal magnetic memory method[J].Experimental Mechanics,2012,52:305-314.

[15]Yang En,Li Luming,Chen Xing.Magnetic field aberration induced by cycle stress[J].Journal of Magnetism and Magnetic Materials,2007,312:72-77.

[16]Kuruzar M E,Cullity B D.The magnetostriction of iron under tensile and compressive stress[J].International Journal of Magnetism,1971,1(14):323-325.

[17]Wang Zhengdao,Yao Kai,Deng Bo,et al.Theoretical studies of metal magnetic memory technique on magnetic flux leakage signals[J].NDT&E International,2010,43:354-359.

10.16450/j.cnki.issn.1004-6801.2017.04.005

* 国家自然科学基金资助项目(51578449，51478383，51378413)；陕西省自然科学基金资助项目(2015JM5192)

2015-04-28；

2015-08-19

TH140.7； TG115.28

易术春，男，1990年9月生，博士生。主要研究方向为金属磁记忆无损检测技术的测试、分析及其应用。曾发表《建筑钢试件拉伸应力与其磁记忆效应漏磁场梯度的对应关系研究》(《西安建筑科技大学学报：自然科学版》2015年第47卷第3期)等论文。 E-mail:yscone@live.xauat.edu.cn