6维三步幂零李代数导子的刻画

苏 鹏，任 斌

（苏州科技大学 数理学院，江苏 苏州 215009）

6维三步幂零李代数导子的刻画

苏 鹏，任 斌*

（苏州科技大学 数理学院，江苏 苏州 215009）

主要研究特征不等于2的域上6维三步幂零李代数的导子代数。文中将6维三步幂零李代数分为三种类型，借助矩阵的计算，刻画了每一类型其导子的结构。

幂零李代数；基；导子

导子代数[1-3]是李代数结构理论[4-7]研究的一个重要方面，也在微分几何、理论物理等其他领域有重要应用。文献[8]得到了三维中心的二步幂零李代数导子的一个充要条件，而关于三步幂零李代数的导子代数，目前这方面的讨论还不多，笔者主要研究了特征不等于2的域上6维三步幂零李代数的导子代数。文献[9]给出了特征不等于2的域上维数小于等于6的幂零李代数的所有分类，其中6维三步幂零李代数N按其N2、N3的维数可归为三种类型，文中刻画了每一类型其导子的结构。根据这些等价条件，能较容易地刻画出N的导子代数的结构，也为进一步研究其导子代数的性质奠定了基础。

文中讨论的李代数N均是特征不等于2的域F上有限维李代数。

1 基本概念和基本结论

定义1[10]有限维李代数N称为幂零的，如果存在正整数i使得Ni=0。若N3≠0，N4=[N3，N]＝0，则称有限维李代数N是三步幂零的。

定义2[10]设N是域F上的李代数，D是N上的一个线性变换。若D满足下述条件

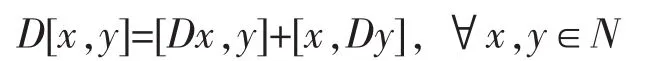
则称D是N的一个导子。记DerN={D∈gl（N）|D是N的导子}。

引理1[11]若N是一个幂零李代数，则下面两个命题等价：

（1）{x1，x2，…，xn}是 N 的一个极小生成元系；

（2）{x1+N2，x2+N2，…，xn+N2}是向量空间 N/N2的一组基。

引理 2 设{x1，x2，…，xn}为李代数 N的一组基，D是 N上的一个线性变换，则 D∈DerN当且仅当D[xi，xj]＝[Dxi，xj]+[xi，Dxj]， 1≤i，j≤n。

定理1[9]设N是特征不等于2的域F上不可分解的6维三步幂零李代数，同构意义下可分为6种：

N6，6：[x1，x2]＝x4，[x1，x3]＝x5，[x1，x4]＝x6。

定义 3 设 N 是一个三步幂零李代数，若 dimN=p+m1，dimN2=m1，dimN3=m2，则称 N 为（m1，m2，p）型的。

不可分解的 6 维三步幂零李代数 N 可分为如下三种类型：（2，1，4）型：N6，1；（3，1，3）型：N6，2（ε）；N6，3，N6，4，N6，6；（3，2，3）型：N6，5（ε）。

2 主要结果

下面将得到每一类型的6维三步幂零李代数导子的一个充要条件。这里所讨论的李代数N均是不可分解的6维三步幂零李代数。

设{x1，x2，x3，x4，x5，x6}为 N 的一组基，若 D 是 N 上的一个线性变换，则有

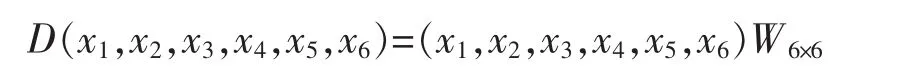
2.1 （2，1，4）型的导子

设 N 是一个（2，1，4）型的，则 N 有一个极小生成元系{x1，x2，x3，x4}。 设{x5，x6}是 N2的一组基，{x6}是 N3的基，于是有 5×5 的反对称矩阵 E=（Eij），F=（Fij）使得[xi，xj]=Eijx5+Fijx6， 1≤i，j≤5。 当 i＝5 或 j＝5 时，Eij＝0。 记 E1＝（Eij）4×4，F1＝（Fij）4×4。

定理2 设N是一个（2，1，4）型的，N的一个线性变换D是导子的充要条件是D对应的矩阵

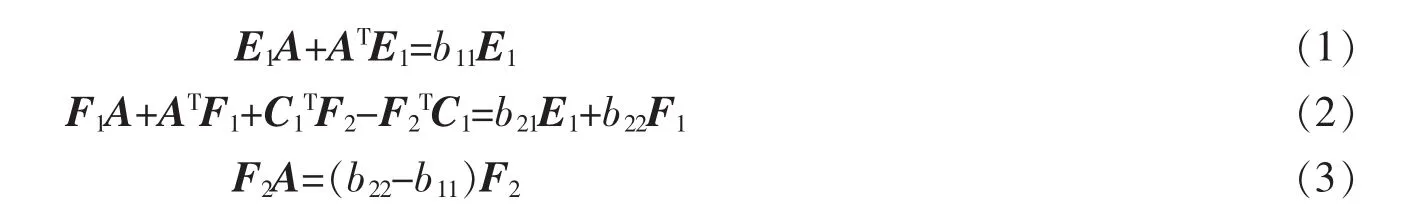
这里 C1＝（a51，a52，a53，a54），F2=（F51，F52，F53，F54）。

证明 必要性 因为 D（x5）∈N2，D（x6）∈N3，所以

由于D是N的一个导子，则有

显然，等式（4）等价于等式（5）、（6）同时成立

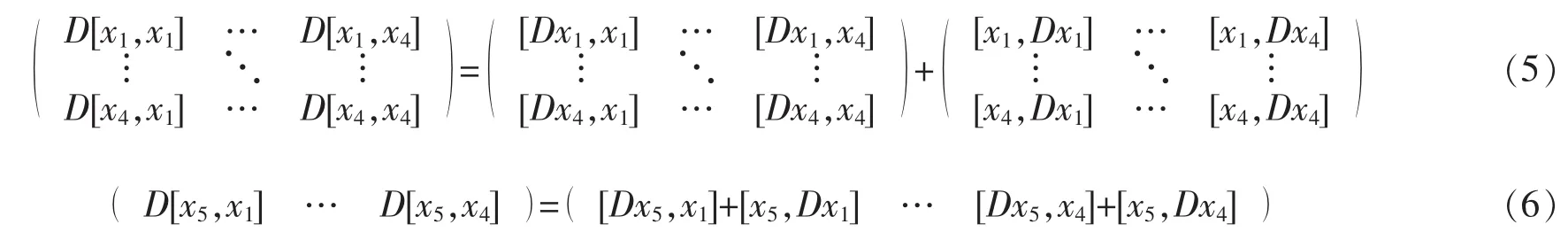
下面将由等式（5）、（6）推出必要性成立，证明如下：

因为[xi，xj]=Eijx5+Fijx6，所以

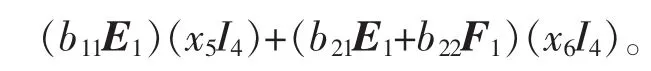
同理可得

故得（5）式右边=（E1A+ATE1）（x5I4）+（F1A+ATF1+C1TF2-F2TC1）（x6I4），所以可得等式（1）、（2）成立。

由等式（6），有 D[x5，xj]＝[Dx5，xj]+[x5，Dxj]，1≤j≤4，注意到

充分性 由必要性的证明过程易证等式（4）成立。由引理2知，D是N的一个导子。

2.2 （3，2，3）型的导子

设 N 是一个（3，2，3）型的，则 N 有一个极小生成元系{x1，x2，x3}。 设{x4，x5，x6}是 N2的一组基，{x5，x6}是 N3的一组基，于是有 4×4 的反对称矩阵 E=（Eij），F=（Fij），J=（Jij）使得

当 i＝4 或 j＝4 时，Eij＝0。 记 E1＝（Eij）3×3，F1＝（Fij）3×3，J1＝（Jij）3×3。

定理3 设N是一个（3，2，3）型的，N的一个线性变换D是导子的充要条件是D对应的矩阵

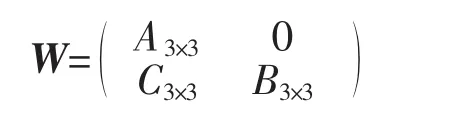
这里 C1＝（a41，a42，a43），F3＝（F41，F42，F43），J2=（J41，J42，J43）。

定理的证明与定理2的证明类似，这里略。

2.3 （3，1，3）型的导子

设 N 是一个（3，1，3）型的，则 N 有一个极小生成元系{x1，x2，x3}。 设{x4，x5，x6}是 N2的一组基，{x6}是 N3的基，于是有 5×5 的反对称矩阵 E=（Eij），F=（Fij），J=（Jij）使得

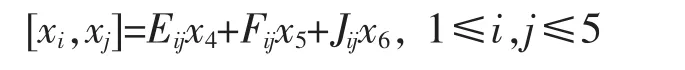
当 i＝4，5 或 j＝4，5 时，Eij＝Fij＝0。 记 E1＝（Eij）3×3，F1＝（Fij）3×3，J1＝（Jij）3×3。

定理4 设N是一个（3，1，3）型的，N的一个线性变换D是导子的充要条件是D对应的矩阵

定理的证明与定理2的证明类似，这里略。

通过以上讨论，得到了每一类型的6维三步幂零李代数N的导子的一个充要条件。根据这些等价条件，能较容易地刻画出N的导子代数。例如利用定理4可较容易地刻画出（3，1，3）型的四种李代数的导子代数，结果如下

[1]范素君，周檬，崔丽娟.幂零李代数的导子代数的结构[J].河北师范大学学报（自然科学版），2009，33（5）：567-569.

[2]巫永萍.5维幂零李代数的导子代数的结构[J].大学数学，2012，28（5）：76-79.

[3]WU Mingzhong.The derivaion algebra of Qnfiliform Lie algebra[J].Chin Quart J Math，2013，28（3）：397-401.

[4]SEELEY C.7-dimensional nilpotent Lie algebra[J].Trans Amer Math Soc，1993，335：479-496.

[5]REN B，ZHU L S.Classification of 2-step nilpotent Lie algebras of dimension 8 with 2-dimensional center[J].Comm Algebra，2011，39：2068-2081.

[6]YAN Z L，DENG S Q.Completable two step nilpotent Lie algebras of type（2，p）[J].Linear and Multilinear Algebra，DOI：10.1080/03081087.2013.780605.

[7]REN B，ZHU L S.Quasi Qnfiliform Lie algebras[J].Algebra Colloquium，2011，18（1）：139-154.

[8]潘林辉，任斌.（3，p）型二步幂零李代数导子的一个充要条件[J].苏州科技学院学报（自然科学版），2014，31（3）：10-13.

[9]WILLEM A DE GRAAF.Classification of 6-dimensional nilpotent Lie algebras over fields of characteristic not 2[J].Computational Algebra，2007，309（2）：640-653.

[10]苏育才，卢才辉，崔一敏.有限维半单李代数简明教程[M].北京：科学出版社，2008.

[11]SANTHAROUNANE L.Kac-Moody Lie algebra and the classification of nilpotent Lie algebra of maxial rank[J].Cannad J Math，1982，34：1215-1239.

Characterization for derivation of three step 6-dimensional nilpotent Lie algebras

SU Peng，REN Bin*
（School of Mathmatics and Physics，SUST，Suzhou 215009，China）

In this paper,we studied the derivation of three step 6-dimensional nilpotent Lie algebras over the fields that characteristics are not 2.We classified the algebras into three types and characterized the structure of the derivation of each type by the calculation of matrix.

nilpotent Lie algebra；base；derivation

O512 MR（2010）Subject Classification：17B05；17B30；17B40

A

2096－3289（2017）03－0025－05

责任编辑：谢金春

2015－12－16

国家自然科学基金资助项目（11271056）

苏 鹏（1989-），女，山西朔州人，硕士研究生，研究方向：代数方向。

*通信作者：任 斌（1964-），男，教授，博士，硕士生导师，E-mail：renbin1964@163.com。