地下水对地基承载力和浅基础沉降的影响

高会贤，史 萍，2，3

(1.山东理工大学 建筑工程学院，山东 淄博 255049； 2.山东省土木工程防灾减灾重点实验室，山东 青岛 266590； 3.山东科技大学 土木工程与建筑学院，山东 青岛 266590)

地下水对地基承载力和浅基础沉降的影响

高会贤1，史 萍1，2，3

(1.山东理工大学 建筑工程学院，山东 淄博 255049； 2.山东省土木工程防灾减灾重点实验室，山东 青岛 266590； 3.山东科技大学 土木工程与建筑学院，山东 青岛 266590)

采用OptumG2有限元软件，分析不同水位埋深对地基承载力和浅基础沉降的影响.研究发现，随着水位的降低，黏聚力和内摩擦角愈大，地基极限承载力愈大，基础沉降愈小.水位埋深较小时黏聚力和内摩擦角对地基承载力和基础沉降的影响较大，随着水位埋深的增大，影响逐渐减小；对于同一水位埋深，黏聚力和内摩擦角愈大，其对地基承载力和基础沉降的影响愈小；相对于内摩擦角而言，黏聚力对地基承载力和基础沉降的影响大.

黏聚力；内摩擦角；承载力；沉降；有限元法

近年来，伴随我国大规模的基础设施建设，地基强度问题引发的工程事故呈上升趋势.国内外学者已经对承载力理论公式和地基承载力确定方法等方面进行了探索[1]，分析了土体基本特性[2-6]、基础形式和尺寸[7-8]、埋深[9]等对地基承载力的影响，而现行规范对地基承载力的计算过程没有考虑地下水位变化的影响.实际在我国北方地区，地下水被大量开采，区域地下水位逐年下降，地下水位变化导致地基承载力不足或基础沉降过大等问题引起的工程事故屡见不鲜，因此分析水文地质条件变化对建筑物地基承载力的影响至关重要.

本文拟应用数值分析方法分析不同水位工况下不同抗剪强度指标对地基承载力和浅基础沉降的影响.

1 有限元分析

对于求解复杂岩土工程问题，有限元方法是强有力的工具.OptumG2是一款集极限分析和有限元分析于一身的岩土分析软件，由世界上首屈一指的有限元分析研究机构OptumCE开发.此软件具有高效的图形交互界面，可以创建各种复杂的有限元模型，为每种实体材料指定相应的排水条件，采用极限分析法计算岩土体破坏时极限荷载的严格上限值和下限值，采用弹塑性法分析正常使用状态和施工阶段状态的各种特性.

1910年，Mohr提出一个假设：当材料某个平面上的剪应力τn达到某个极限值时，材料发生屈服.这也是一种剪应力屈服条件，但是与Tresca屈服条件不同，Mohr假设的这个极限值不是一个常数值，而是与该平面上的正应力σn有关，它可以表示为τn=f(c,φ,σn).上式中，C是土的黏聚力，φ是土的内摩擦角，这个函数关系式可以通过实验确定.一般情况下，材料的内摩擦角随着静水压力的增加而逐渐减小，因而假定函数对应的曲线在σn-τn平面上呈双曲线或抛物线或摆线。但在静水压力不大的情况下，屈服曲线常用φ为定值的直线来代替，它可以表示为

τn=c+σntanφ

(1)

式(1)称为Mohr-Coulomb屈服条件.

2 材料力学参数及计算模型

本模型中地基土为饱和黏土，选择Mohr—Coulomb准则作为岩土材料本构模型，各参数取值见表1.

表1 本构模型所用参数

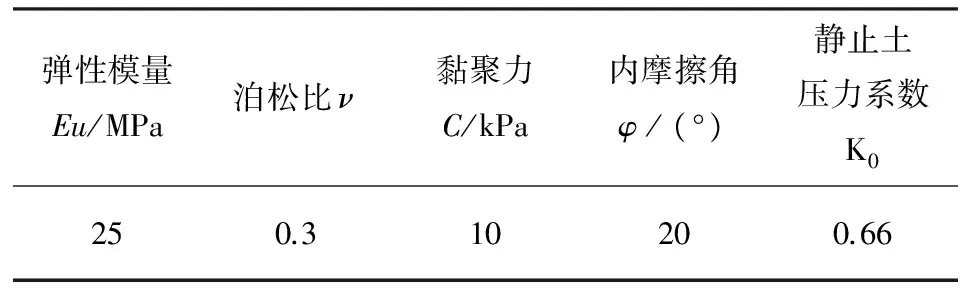
弹性模量Eu/MPa泊松比ν黏聚力C/kPa内摩擦角φ/(°)静止土压力系数K0250．310200．66

分别考虑不设置水位工况、在室外地面及室外地面以下1.5m、2.5m、3.5m、4.5m高度定义静水位等各种工况，对于设置水位的工况，采用线性水力模型.基础采用刚性材料模拟，其重度为24kN/m3，基础底面宽度为3m，基础埋深2m，边界条件选择“标准边界条件”，基础上部施加偏心荷载，创建的几何模型如图1所示.

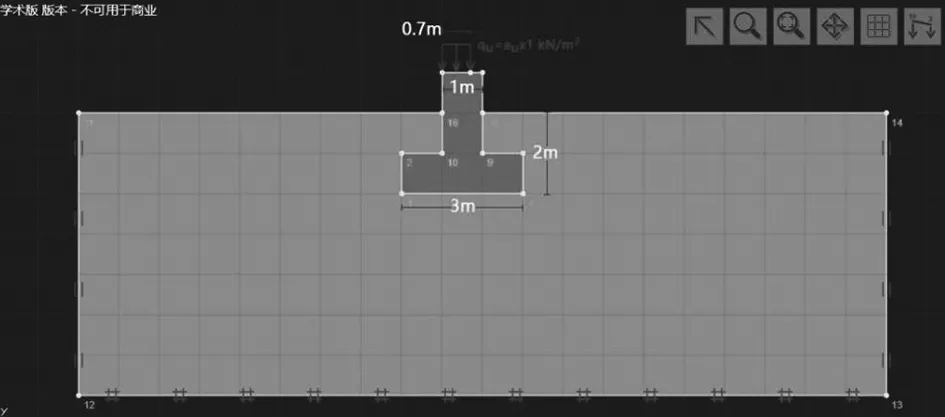
图1 几何模型图

3 数值分析

3.1 地基承载力分析

采用极限分析得到地基承载力，分析时区分长期和短期条件，为了得到不同单元数的影响大小，“单元数量”分别设置为 1000、2000、4000，其计算结果分别为：

qu=697.4kN/m3±4.3%，

qu=695.8kN/m3±2.5%，

qu=696.8kN/m3±1.6%.

由以上三个式子可知，虽然网格单元数量从 1000 上升至 4000，计算误差减小了近 3 倍，但是计算平均值的差异只有 1%.在有限元分析中，平均值相对于上限解和下限解的误差往往夸大了平均值的真实误差，真实值相对于上限解和下限解的误差总是趋于相同，这使得平均值往往更接近真实值.

3.2 基础沉降分析

假设荷载作用在基础上的速度足够快，那么需要考虑不排水条件，然后保持荷载作用不变，直到超静孔隙水压力完全消散.因此，整个分析中既要考虑短期条件，又要考虑长期条件，两个工况阶段均采用1000 个 6节点高斯单元和 3 步自适应迭代，图 2中给出了相应的变形计算结果.可以注意到，主要的变形均发生在短期工况阶段， 即相对于瞬时变形而言，固结效应对变形的影响相对较小.

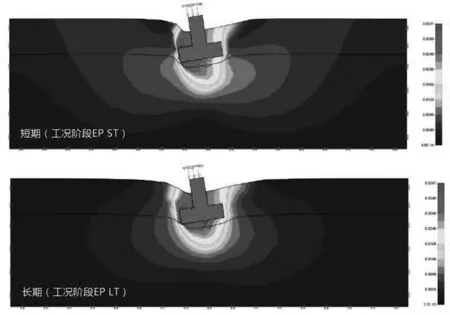
图2 基础的位移矢量图(变形放大系数为30)

4 结果分析

查询工程地质手册[10]，本文将地基土的黏聚力取值范围定为5kPa～55kPa，内摩擦角的取值范围定为5°～45°.选用两个量化指标来评价水位深度和黏聚力、内摩擦角对地基承载力的影响，其一是沉降比(settlement ratio,SR)，定义为不同工况的基础最大沉降量与无水位时基础最大沉降量的比值，计算公式如下：

式中：S为不同工况的基础最大沉降量，S0为无水位时基础的最大沉降量，如果SR小于1.0，说明该工况的基础沉降量比无水位时的基础沉降量小.

另一个指标是承载力比(bearing capacity ratio,BCR)，定义为不同工况的地基承载力与无水位时地基承载力的比值，计算公式如下：

式中：q为不同工况的地基承载力，q0为无水位时地基承载力.BCR越接近1.0，水位对基础承载力的影响越小.

土体黏聚力和内摩擦角对地基承载力和基础沉降的影响分析如图3—图6所示.

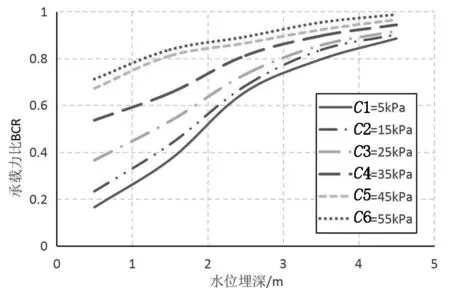
图3 黏聚力对承载力比的影响

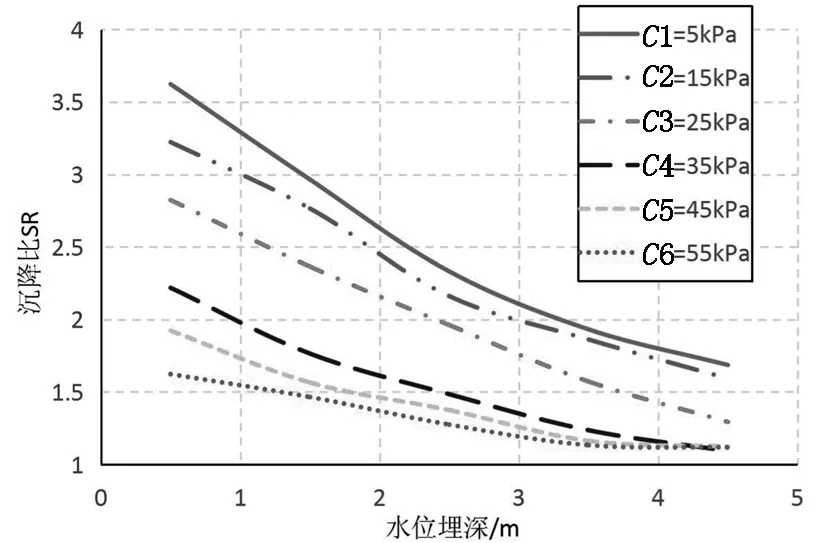
图4 黏聚力对沉降比的影响

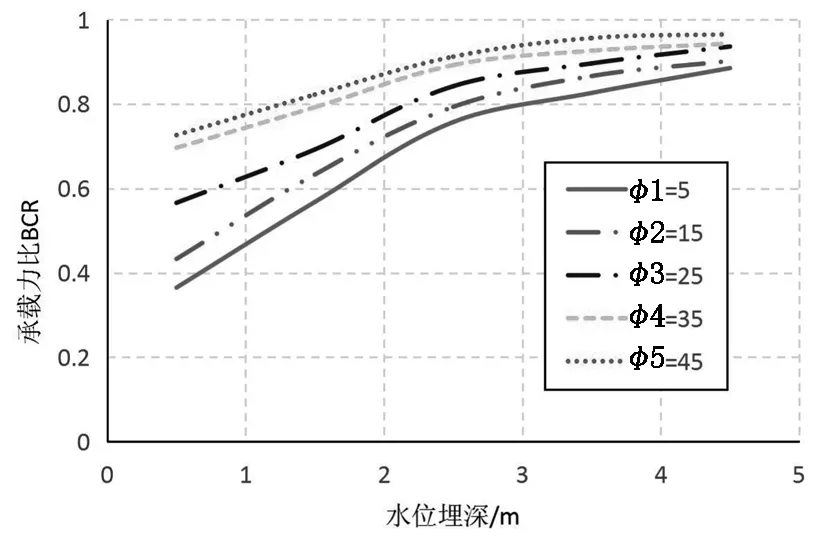
图5 内摩擦角对承载力比的影响

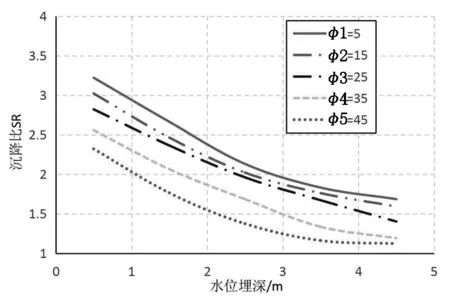
图6 内摩擦角对沉降比的影响

由图3和图5可得，水位埋深从0到4.5m 变化过程中，随着黏聚力和内摩擦角的增大，地基极限承载力逐渐增大.水位埋深较小时黏聚力和内摩擦角对地基承载力的影响较大，随着水位埋深的增大，影响逐渐减小.对于同一水位埋深，黏聚力和内摩擦角愈大，其对地基承载力的影响愈小.产生以上现象的原因是：在水位下降过程中，孔隙水压力减小导致有效应力增大，土体抗剪强度增大使得地基承载力增大. 当土体黏聚力和内摩擦角增大到一定程度时，土体的抗剪强度较大，此时地基承载力不会受太大影响.

由图4和图6可得，随着黏聚力和内摩擦角的增大，基础沉降逐渐减小.水位埋深较小时黏聚力和内摩擦角对基础沉降的影响较大，随着水位埋深的增大，影响逐渐减小.对于同一水位埋深，黏聚力和内摩擦角愈大，其对基础沉降的影响愈小.这是因为，随着黏聚力和内摩擦角的增大,地基破坏的控制标准由地基强度转为基础变形.黏聚力为5kPa、15kPa、25kPa和内摩擦角为5°、15°时的地基破坏时，基础两侧的地表土有明显挤出，地基破坏贯通到地表，此时的基础变形仍然能够满足要求，为整体剪切破坏的特征；当黏聚力增大到35Pa、45kPa和内摩擦角为25°时，基础两侧的地表隆起减少，地表土挤出不明显，此时基础的沉降很大，破坏是由基础的变形控制的；当黏聚力增大到55kPa、内摩擦角为45°时，基础两侧小范围内的地表土发生沉降，地基破坏未发展到地表.

相对于内摩擦角而言，黏聚力对地基承载力和基础沉降的影响大.

5 结论

采用集极限分析和有限元分析于一身的岩土分析软件OptumG2对无水位和不同水位埋深时的地基承载力和浅基础沉降进行数值分析，得出以下结论：

(1)在有限元分析中，设置的网格单元数量越多，计算误差越小，但是相对于平均值的差异只有 1%，而且平均值更接近真实值.

(2)基础的变形主要发生在短期工况阶段，即相对于瞬时变形而言，固结效应对变形的影响相对较小.

(3)黏聚力和内摩擦角越大，地基极限承载力越大.随水位埋深的增大，其对地基承载力的影响影响逐渐减小.而且，对于同一水位埋深，黏聚力和内摩擦角愈大，其对地基承载力的影响愈小.

(4)黏聚力和内摩擦角越大，基础沉降越小.随水位埋深的增大，其对沉降比的影响逐渐减小.对于同一水位埋深，黏聚力和内摩擦角愈大，其对基础沉降的影响愈小.

(5)相对于内摩擦角而言，黏聚力对地基承载力和基础沉降的影响大.

[1]马庆宏.浅基础地基承载力研究进展[J].防灾减灾工程学报,2014，34(增):120-128.

[2] 阮怀宁.广义极限平衡理论在地基与边坡稳定分析中的应用[J].水利学报,1996(4)：46-56.

[3] GRIFFTHS D V, FENTON G A, MANOHARAN N. Bearing capacity of rough rigid strip footing on cohesive soil: probabilistic study[J]. Journal of Geotechnical and Geo-environmental Engineering ,2002 ,128(9)：743-755.

[4] 徐干成,李成学,刘平.各向异性和非均质地基土上浅基础的极限承载力[J].岩土工程学报,2007(2)：164-168.

[5] AZAMI A,PIETRUSZCZAK S,GUN P. Bearing capacity of shallow foundations in transversely isotropic granular media[J]. International Journal for Numerical and Analytical Methods in Geomechanics,2010,4(8)：771-793.

[6]BENMEBAREK S,REMADNA M S, BENMEBAREK N.Numerical evaluation of the bearing capacity factor N of ring footings[J].Computers and Geotechnics ,2012(44)：132-138.

[7] LOUKIDIS D,SALGADO R.Bearing capacity of strip and circular footings in sand using finite elements[J]. Computers and Geotechnics,2009,36(5)：871-879.

[8] 杜佐龙,黄茂松,秦会来.基底宽度对承载力系数N_γ的影响分析[J]. 岩土工程学报,2010(3)：408-414.

[9] CHOUDHURRY D, SUBBA K.Seismic bearing capacity of shallow strip footings embedded in slope[J]. International Journal of Geomechanics,2006,6(3)：176-184.

[10]工程地质手册编委会.工程地质手册[Z].4版.北京:中国建筑工业出版社，2006.

(编辑：姚佳良)

Study on bearing capacity and settlement of shallow foundation with underground water

GAO Hui-xian1，SHI Ping1，2，3

(1. School of Architecture Engineering， Shandong University of Technology, Zibo 255049， China； 2. Key Laboratory of Civil Engineering Disaster Prevention and Mitigation， Qingdao 266590， China； 3. College of Architecture and Civil Engineering， Shandong University of Science and Technology， Qingdao 266590， China)

The influence of different underground water on shallow foundation is investigated. The result proves that with the lower water level, the ultimate bearing capacity of foundation is bigger and the settlement is smaller with the cohesion and internal friction angle increasing. When the water level is low, the cohesion force and internal friction angle of foundation greatly influence the bearing capacity and foundation settlement. However, with the water level increasing, the influence is smaller. As the same water level, the more cohesion and internal friction angle, the smaller effect of bearing capacity and foundation settlement .Relative to the friction angle, the cohesion forcegreatly influence the bearing capacity and foundation settlement.

cohesion force；friction angle；bearing capacity；foundation settlement；finite element method

2017-03-06

山东省土木工程防灾减灾重点实验室开放基金项目(CDPM2013KF02)

高会贤，男，jgxyhx@126.com； 通信作者：史萍, 女, shiping0813@163.com

1672-6197(2017)06-0022-04

TU443

A