混凝土收缩徐变效应对含叠合梁段混合梁斜拉桥主梁受力行为的影响
唐继舜,李海岗,陈远久,田 欣
(西南交通大学 土木工程学院,四川 成都 610031)
混凝土收缩徐变效应对含叠合梁段混合梁斜拉桥主梁受力行为的影响
唐继舜,李海岗,陈远久,田 欣
(西南交通大学 土木工程学院,四川 成都 610031)
以某双塔混合梁斜拉桥为工程背景,利用桥梁专业软件Midas/Civil建立了全桥三维有限元模型;对比分析了在成桥阶段混凝土收缩徐变作用对斜拉桥主梁内力行为的影响.分析结果表明:混凝土收缩徐变效应对叠合主梁弯矩的影响较大,使其发生了内力重分布,对正弯矩具有削峰作用,造成负弯矩值有较大的增加,对混凝土主梁影响较小;收缩徐变效应对主梁轴力及剪力的影响均较小;混凝土的收缩徐变效应对叠合梁的受力影响较大,使叠合梁中钢梁与混凝土桥面板之间应力发生重分布,靠近钢-混凝土结合段处的混凝土主梁应力改变较大,其余位置改变量不明显.
混合梁;斜拉桥;叠合梁;收缩徐变;受力行为
混凝土在空气中凝固和硬化过程中,体积减小的现象称为收缩,通常认为混凝土收缩是由凝胶体本身收缩和混凝土因失水产生的体积收缩组成[1].混凝土徐变是由于水泥石凝胶体在长期荷载作用下的黏性流动或滑移,同时吸附在凝胶粒子上的吸附水因荷载应力而向毛细管渗出.徐变是在应力作用下产生的,而收缩的产生则与应力无关,收缩徐变变形的特点是早期发展迅速,后期发展缓慢.因此收缩徐变影响着混凝土的各方面性能,如导致混凝土开裂和降低其耐久性[2].混凝土收缩、徐变使得混凝土结构的变形随着时间而发生较大的变化,而当这些变形发生在超静定结构中时,在多余约束处会产生多余的约束力,从而也就产生了次内力,这就是混凝土收缩和徐变的影响力[3].
混合梁斜拉桥是指斜拉桥的主梁有两种不同的材料组成,主跨的梁体为钢材,边跨的梁体为混凝土梁材料[4-6].在大跨桥梁结构中,通常对主跨的主梁有一定的刚度要求,因此主跨主梁采用叠合梁形式,则形成含有叠合梁段的混合梁斜拉桥.
由于混凝土收缩徐变效应可导致结构的变形增加、预应力损失以及内力重分配,因此对含叠合梁段混合梁斜拉桥结构的分析中需要重视混凝土收缩徐变效应.对收缩徐变进行准确分析,找出主梁在收缩徐变效应下内力的变化规律和变化趋势,这对保证该类斜拉桥的结构安全和正常使用具有重要的意义[7].
1 工程概况
该斜拉桥为双塔混合梁斜拉桥(280m+572m+198m).主桥结构型式为双塔、双索面、密索体系斜拉桥.主梁为纵向半漂浮体系,主跨跨径为572m,两岸边跨跨径分别为280m和198m.北岸为辅助通航孔区,南岸不受通航影响,因此南岸边跨布置3个辅助墩.主桥全长1050m,该桥总体布置如图1所示.主跨及北岸边跨主梁采用双纵肋叠合梁,钢主梁为工字形断面,叠合梁中心梁高3.5m.叠合梁主横隔板标准间距为13.5m,主横隔板间设置次横隔板,间距为4.5m.南岸边跨主梁采用双纵肋混凝土主梁,中心梁高3.5m.叠合梁和混凝土主梁结合部采用钢-混凝土过渡段连接,结合部位于中跨侧距离南岸索塔10.725m处.混凝土主梁采用C60等级的混凝土,钢梁采用Q370qD结构钢.
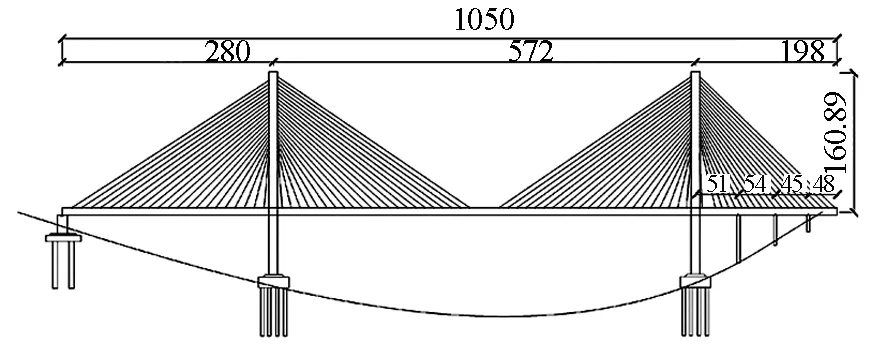
图1 主桥总体布置图(尺寸单位:m)
2 有限元模型
论文采用大型桥梁通用软件Midas/Civil建立全桥空间有限元模型(图2),主梁采用单主梁模式,斜拉索采用索单元,叠合梁采用施工阶段联合截面法[8];桥面板采用预制拼装,并且预制板在拼装之前存放6个月,拉索锚固区采用现浇;混凝土材料的收缩徐变系数曲线以10000d为终值;依据实际施工步骤,该桥共划分152个施工阶段.对于交界墩,在实际支座的位置建立上下两个节点,节点之间采用弹性连接,弹性连接刚度按支座的实际刚度输入.有限元模型中单元编号见表1.
表1 全桥有限元模型主梁分布

单元号叠合梁混凝土梁1-8283-249250-311主梁分布北岸边跨主跨南岸边跨

图2 全桥空间有限元模型
3 有限元分析结果
3.1 对主梁轴力的影响
根据全桥有限元模型的计算结果,主梁在成桥阶段开始和成桥后10000d两个时间点的轴力值如图3所示.
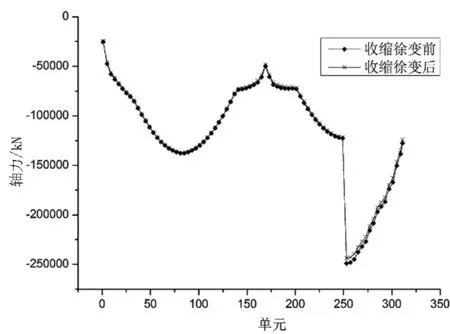
图3 成桥阶段不同时刻主梁轴力值
由图3可以看出:斜拉桥的最大轴力值均发生在南岸桥塔处,成桥阶段收缩徐变对主梁的轴力值影响较小,对叠合梁段的影响相对更小.各控制截面两个时刻的轴力值对比见表2.
表2 成桥阶段主梁控制截面收缩徐变前后轴力对比
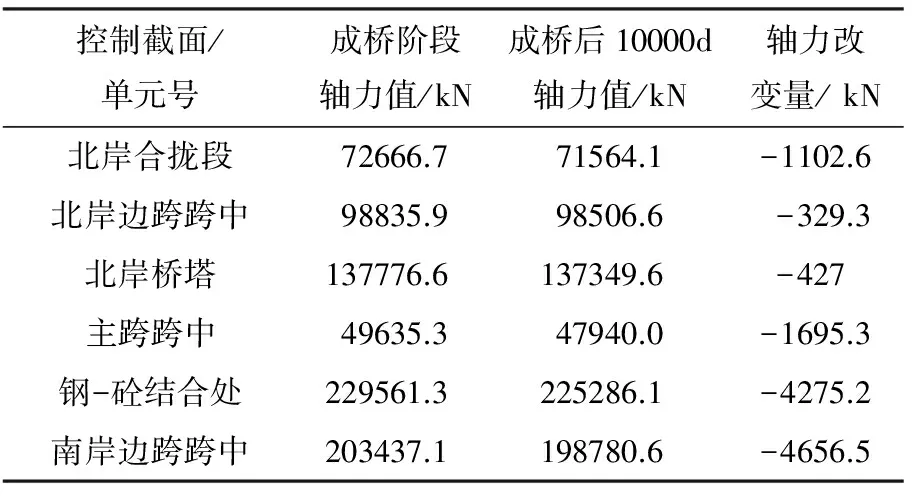
控制截面/单元号成桥阶段轴力值/kN成桥后10000d轴力值/kN轴力改变量/kN北岸合拢段72666.771564.1-1102.6北岸边跨跨中98835.998506.6-329.3北岸桥塔137776.6137349.6-427主跨跨中49635.347940.0-1695.3钢-砼结合处229561.3225286.1-4275.2南岸边跨跨中203437.1198780.6-4656.5
3.2 对主梁弯矩的影响
根据全桥有限元模型的计算结果,主梁在成桥阶段开始和成桥后10000d两个时间点的弯矩值如图4所示.

图4 成桥阶段不同时刻主梁弯矩值
由图4可知,成桥阶段混凝土收缩徐变对叠合梁主梁弯矩值的影响较大,而对混凝土主梁的弯矩值影响相对较小.不同时刻叠合梁主梁最大正弯矩均发生在北岸边跨靠近交界墩处,混凝土收缩徐变发生后,在靠近南北桥塔处叠合梁的弯矩值符号发生改变,且产生的负弯矩值比较大,最大负弯矩值为-45785.7kN·m;叠合梁主梁正弯矩有所减小,且正弯矩峰值减幅达到33.9%,也就是混凝土收缩徐变效应对叠合主梁产生了内力重分布,因而对正弯
表3 成桥阶段主梁控制截面收缩徐变前后弯矩对比

控制截面/单元号成桥阶段弯矩值/kN·m成桥后10000d弯矩值/kN·m弯矩改变量/kN·m北岸1/4边跨76428.350522.6-25905.7北岸边跨跨中40173.44175.0-35998.4北岸桥塔9645.7-38858.7变号主跨跨中47496.224824.7-22671.5钢-砼结合处22582.86-4156.89变号南岸边跨跨中-5341.8-3888.8-1453.0
矩具有削峰的作用.成桥阶段混凝土收缩徐变效应对各控制截面的弯矩值见表3.
3.3 对主梁剪力的影响
根据全桥有限元模型的计算结果,主梁在成桥阶段开始和成桥后10000d两个时间点的剪力值如图5所示.
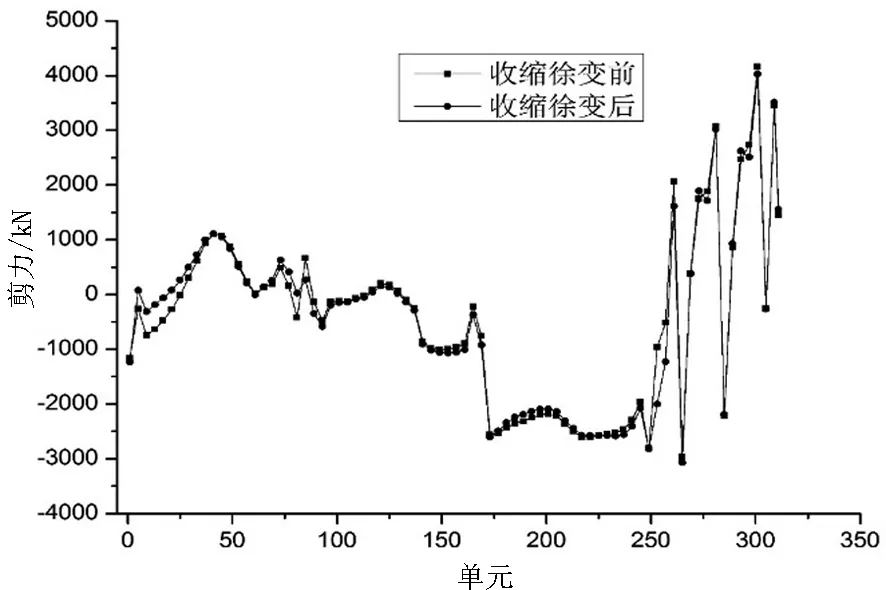
图5 成桥阶段不同时刻主梁剪力值
由图5可知,成桥阶段混凝土收缩徐变对主梁剪力值影响较小.成桥阶段最大剪力值为6609kN,混凝土收缩徐变完成后最大剪力值为6503kN,主梁的最大剪力值均发生在南岸桥塔钢-混凝土结合段处,控制截面剪力值见表4.
表4 成桥阶段主梁控制截面收缩徐变前后剪力对比

控制截面成桥阶段剪力值/kN成桥后10000d剪力值/kN剪力改变量/kN北岸合拢段717.51069.5351.6北岸边跨跨中2082.52094.912.4北岸桥塔-2961-3354.1393.1主跨跨中52.1-115.1变号钢-砼结合处-6609-6503106南岸边跨跨中3460.53454.6-5.9
3.4 叠合梁应力分析
叠合梁中钢主梁与混凝土桥面板在成桥阶段开始和成桥后10000d两个时间点的应力变化情况见图6、图7及表5、表6.

图6 成桥阶段不同时刻钢梁应力值
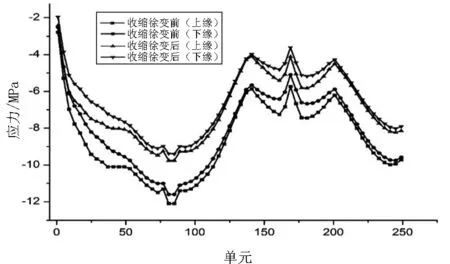
图7 成桥阶段不同时刻混凝土桥面板应力值
由图6、图7及表5、表6可知,成桥阶段混凝土的收缩徐变效应未使混凝土桥面板出现拉应力,混凝土桥面板的最大压应力出现在北岸桥塔处;在主跨跨中以及北岸边跨交界墩处,钢主梁下缘出现拉应力,拉应力数值较小;钢主梁的上下翼缘的压应力均有所增加,压应力最大增幅达到232.6%,位于北岸桥塔处;而混凝土桥面板的压应力均减小,最大减幅为29.4%,位于主跨跨中.由此可知:在混凝土的收缩徐变作用下,叠合梁截面发生了应力重分布[9-10].
表5 成桥阶段钢主梁收缩徐变前后应力值对比
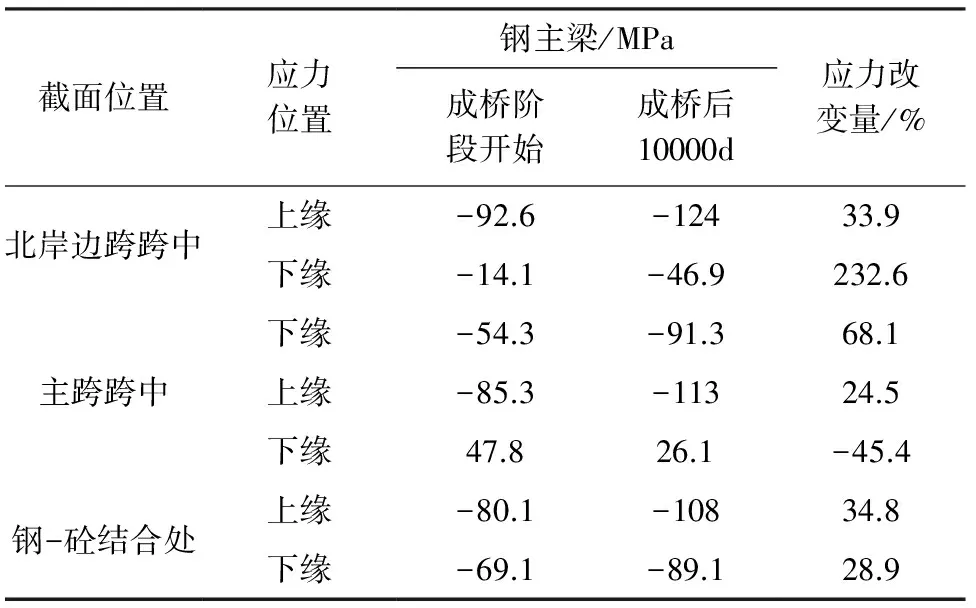
截面位置应力位置钢主梁/MPa成桥阶段开始成桥后10000d应力改变量/%北岸边跨跨中上缘-92.6-12433.9下缘-14.1-46.9232.6主跨跨中下缘-54.3-91.368.1上缘-85.3-11324.5下缘47.826.1-45.4钢-砼结合处上缘-80.1-10834.8下缘-69.1-89.128.9
表6 成桥阶段混凝土桥面板收缩徐变前后应力对比

桥面板/MPa控制截面位置应力位置成桥阶段开始成桥后10000d应力改变量/%北岸边跨上缘-10.3-8.2-20.4下缘-9.4-7.6-19.2北岸桥塔上缘-11.7-9.2-21.4下缘-11.3-9.0-20.4主跨跨中上缘-5.8-4.1-29.3下缘-5.1-3.6-29.4钢-混凝土结合处上缘-9.7-8.2-15.5下缘-9.6-7.9-17.7
3.5 混凝土主梁应力分析
混凝土主梁在成桥阶段开始和成桥后10000d两个时间点的应力变化情况见图8及表7.

图8 成桥阶段不同时刻混凝土主梁上缘应力值
由图8及表7可知,成桥阶段混凝土的收缩徐变效应使混凝土主梁的上翼缘应力有所降低,靠近钢-混凝土结合段处的影响比较大,最大降幅13.2%;在靠近钢-混凝土结合段处的混凝土主梁下翼缘应力增加,最大增幅32.5%,其余位置均有所降低,混凝土收缩徐变效应对南岸辅助墩位置处混凝土主梁下翼缘应力没有明显的影响.
表7 成桥阶段混凝土主梁收缩徐变前后应力值对比

混凝土主梁/MPa控制截面位置应力位置成桥阶段开始成桥后10000d应力改变量/%钢-混凝土结合处上缘-8.8-7.7-12.5下缘-6.8-9.032.4南岸桥塔上缘-7.6-6.6-13.2下缘-5.6-7.025南岸辅助墩上缘-6.5-6.3-3.1下缘-6.0-6.00南岸辅助墩上缘-5.6-5.4-3.6下缘-4.5-4.50
4 结论
由以上分析可以得出,成桥阶段混凝土收缩徐变效应对该斜拉桥主梁的受力状态有较大的影响,具体影响规律如下:
(1)混凝土后期收缩徐变效应对主梁的轴力值影响较小,主梁的轴力改变量不大.
(2)混凝土后期收缩徐变效应对叠合梁主梁弯矩值的影响较大,而对混凝土主梁的弯矩值影响相对较小,混凝土的收缩徐变效应对叠合主梁产生了内力重分布.
(3)混凝土后期收缩徐变效应对主梁剪力值影响较小,主梁的剪力改变量不大.
(4)混凝土后期收缩徐变效应造成了钢主梁与混凝土桥面板之间发生了内力重分配,钢主梁的应力增加,最大增幅232.6%,桥面板的应力有所减小,最大减幅29.4%.收缩徐变效应使钢主梁压应力增加,设计时应重视腹板及下翼缘的稳定问题.
(5)靠近钢-混凝土结合段处混凝土主梁的下翼缘应力增加,最大增幅32.5%,在辅助墩处混凝土主梁下翼缘应力改变量较小;上翼缘应力均有所降低,靠近钢-混凝土结合段处最大减幅为13.2%.
(6)混凝土后期收缩徐变效应对混凝土主梁受力的影响相对较小;对叠合梁主梁受力影响较大.
通过对比分析在成桥阶段混凝土的收缩徐变效应对该斜拉桥主梁内力的影响规律可知:混凝土后期收缩徐变效应对混凝土主梁受力的影响相对较小;对叠合梁主梁受力影响较大.相关研究结论可为同类桥梁的设计、施工及成桥后的研究分析提供重要的参考,设计和施工中应采取相应的措施减少混凝土的后期收缩徐变,保证该类斜拉桥的结构安全和正常使用.
[1]李乔. 混凝土结构设计原理[M]. 北京:中国铁道出版社,2010.
[2]郑军. 混凝土收缩徐变对斜拉桥受力性能的影响[J].太原科技大学学报,2013(1):68-73.
[3]姚玲森. 桥梁工程[M]. 北京:人民交通出版社.2008.
[4]姚康宁.大跨度混凝土斜拉桥运营阶段混凝土收缩徐变影响研究[D].长沙:长沙理工大学,2006.
[5]李忠平,侯登高,吕凯.钢-混凝土混合梁桥设计[J].市政技术,2015(5):48-50.
[6]柴加兵. 钢混叠合梁桥设计与分析[J].北方交通,2015(1):29-32.
[7]李小锋,宋景涛. 收缩徐变效应对混凝土斜拉桥内力状态影响分析[J].上海公路,2015(3):40-42.
[8]葛俊颖. 桥梁工程软件midas Civil使用指南[M].北京:人民交通出版社,2013.
[9]李法雄,王晓夫,黄厚卿,等. 钢-混凝土组合梁斜拉桥收缩徐变影响[J].公路交通科技,2013(10):54-60.
[10]陈亮,邵长宇. 结合梁斜拉桥混凝土收缩徐变影响规律[J].桥梁建设,2015(1):74-78.
(编辑:姚佳良)
Effect of concrete shrinkage and creep effection on the main girder′s mechanic behaviors of hybrid girder cable-stayed bridge with superposed beam
TANG Ji-shun,LI Hai-gang,CHEN Yuan-jiu,TIAN Xin
(School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,China)
The 3D finite element model of a hybrid beam cable-stayed bridge with double pylons located in china is established. Compared with the concrete beam, the effect of shrinkage and creep of concrete on the superposed beam is studied during finished state. And it turns out that the effect of shrinkage and creep of concrete on the superposed beam is much larger than the concrete beam as it leads to bending redistribution and curving pare peak that the negative bending increased. While, it has little effect on the axial force and shear force. Consequently, the stress of superposed beam is redistributed and the stress change of concrete segments near the steel-concrete composite structure is much larger while the others′ is slight.
hybrid girder;cable-stayed bridge;superposed beam;shrinkage and creep;mechanic behaviors
2016-11-29
唐继舜,男,tjstjs1963@163.com
1672-6197(2017)06-0067-05
U448.27;U448.38
A

