基于改进PSO算法的含分布式电源的配电网优化

张丽馨，刘 伟

(山东理工大学 电气与电子工程学院，山东 淄博255049)

基于改进PSO算法的含分布式电源的配电网优化

张丽馨，刘 伟

(山东理工大学 电气与电子工程学院，山东 淄博255049)

为了对含分布式电源的配电网进行规划，提出了考虑配网实际运行约束下以配电网网络损耗、电压偏移及DG投资运行成本为目标函数的多目标优化模型.采用基于Levy Flights的粒子群优化算法对所构造模型进行优化，并对33节点配网系统进行仿真.结果表明所建模型是合理的，改进的PSO算法对求解含DG的配电网多目标优化问题是有效可行的.

分布式电源；配电网；多目标优化；PSO算法；Levy Flights

分布式电源(DG)分布在用户侧，是满足用户需求并支持配网运行的环境兼容型独立发电系统[1].DG并入配电网，能够降低配网网损，提高电力系统灵活性、可靠性及其稳定运行能力[2].但与集中式大电网相比，大量DG并网不仅会改变系统的潮流分布与运行方式，增大配网保护电流，还会造成线路过电压，降低电能质量[3].在解决DG并网问题上，国内外学者多以有功网损为目标函数进行配网的单目标优化[4]，无法兼顾配电网电压偏移、DG投资运行成本等重要指标，同时忽略了多类型DG配合并网问题.基于此，本文综合考虑以电压电流分布参数、安装DG容量位置、功率平衡等为配网拓扑约束，构建计及配网网络损耗、电压偏移量及DG投资运行成本的多目标多约束优化模型[5].目前，多采用启发式算法如PSO算法解决配网规划问题，但PSO算法中粒子的“惰性”较高.为求解所建模型，本文采用改进的PSO算法，该算法能够兼顾种群各个粒子的能力，跳出局部最优，克服PSO算法搜索效率低的缺点.在33节点配网系统中，通过对DG并网前后配电网状态、单目标与多目标优化及算法改进前后的优化结果进行比较，表明所提模型及算法在实现DG并网的综合效益最大化具有一定现实意义.

1 模型构建

1.1 多类型DG的数学模型

DG并网后，其并网节点无法等效于传统节点.根据DG并网运行情况以及出力特性，可将DG并网节点分为PQ型、PV型以及PI型三种类型.根据文献[6-7]构建这三种节点类型的DG数学模型.

1.2 含DG的配网多目标函数模型

以配网网损、电压偏移量、DG投资运行成本为目标函数，构建含DG的配网多目标多约束函数模型.

1.2.1 网损目标函数模型

DG并入配电网，通过减小线路潮流流动来减小配电网网络损耗.网损函数为

(1)

式中：Ploss为网络损耗；L为系统支路数；ri为第i条支路电阻；Pi为第i条支路末端有功功率；Qi为第i条支路末端无功功率；Ui为第i条支路末节点电压.

1.2.2 电压偏移函数模型

节点电压偏移指标是表征配网系统实际运行情况的基本指标，因此以DG并网后电压偏移量为目标函数

(2)

式中：ΔU为电压偏移量；N为配电网节点数；UiN为节点额定电压.

1.2.3DG投资运行成本函数模型

DG并网后，在保证电力系统稳定的前提下，尽量使DG投资运行成本最小，故以其投资运行成本为目标函数

(3)

式中：CDG为投资运行成本；Tmax1为最大年发电时间；η为功率因数；SDG为容量；c1、c2、c3分别为投资、运维及燃料费用；r为年利率；m为使用年限.

1.2.4 多目标归一化函数模型

将网损目标函数、电压偏移函数及DG投资运行成本函数归一化，构造多目标归一化函数模型

(4)

式中：F为多目标归一化函数模型；CL为配电网网损费用；CU为电压偏移指标费用；Tmax2为最大年负荷利用小时数；c4、c5分别为单位电价及电压偏差特征指标价格；Svd为电压偏差指标；wi为权重系数.

1.3 系统约束条件

1.3.1 节点电压约束

(5)

式中Uimax、Uimin为节点电压的上下限.

1.3.2 电流约束

Ii≤Iimax

(6)

式中：Ii为支路电流；Iimax为支路电流上限.

1.3.3 功率平衡约束

(7)

式中：PD、QD为配电网电源的有功、无功功率；PDG、QDG为并网DG的有功、无功功率；Pload、Qload为系统负荷消耗的有功、无功功率.

1.3.4 DG容量约束

(8)

式中：NDGi为第i个节点安装数量；Nimax为第i个节点允许安装最大数量；NDGT为配电网安装的总数量；NTmax为配电网允许安装的最大总数量；SDGi为第i个节点安装DG容量大小；Simax、Simin为第i个节点允许安装DG容量最大值与最小值；SDGT为配电网并网DG总容量；ST为配电网总负荷容量.

2 PSO算法的改进及其实现步骤

2.1PSO算法基本原理

PSO算法是一种通过模拟鱼群和鸟群等群居动物的简化社会行为而发展起来的启发式算法.相较于其它的启发式算法如遗传算法，PSO算法求解效率高、稳定性高，具有一定的抗干扰能力.PSO算法以其优越的全局搜索特性和快速收敛特性，在解决电力系统负荷经济分配、电网规划等问题中得到了成功的应用.

j维空间中的粒子是做随机运动的.随机初始第i个粒子的速度vi,j=(vi,1,vi,2,…,vi,j)和位置xi,j=(xi,1,xi,2,…,xi,j)，粒子通过个体最优解pi,j=(pi,1,pi,2,…,pi,j)及全局最优解gj=(g1,g2,…,gj)来更新自己的速度和位置.公式如下：

(9)

式中：w为惯性权重；c1和c2为学习因子；r1和r2为0到1之间均匀分布的随机数；t为迭代次数.

在PSO算法中，每一代种群中的粒子随当前的最优粒子在解空间中搜索，只能学习当前最优粒子的信息而忽略种群中其它粒子的信息，无法保证种群多样性，当求解复杂的多模态高维优化问题时，PSO算法易出现陷入局部最优解、求解效率降低、收敛精度不高等问题.为缓解PSO算法的上述缺点，本文提出基于Levy Flights[8]更新机制的PSO-LF算法.

2.2PSO算法的改进

PSO-LF算法是对传统PSO算法的改进.同PSO算法相一致，首先对群体粒子的位置xi,j=(xi,1,xi,2,…,xi,j)和速度vi,j=(vi,1,vi,2,…,vi,j)进行随机初始，将各粒子适应度最优的位置存放于pi,j中，将所有pi,j中适应度最优的位置存放于gj中.然后，80%的粒子采用PSO算法的更新方式，20%的粒子采用LevyFlights的更新方式，将各粒子当前适应度与其之前最优位置的适应度作比较，如果较好，更新pi,j，将当前全部pi,j中粒子适应度与gj中粒子适应度作比较，如果较好，更新gj.下面介绍Levy Flights的更新方式.

Levy随机分布通常以简化形式出现：

(10)

式中:si,j为j维空间中第i个粒子的随机步长值，在解空间中，由于LevyFlights方差的变化速度快于布朗运动方差σ2(si,j)～si,j的变化速度，因而LevyFlights比布朗运动的搜索效率还要更高.下式为LevyFlights方差

σ2(si,j)～si,j3-β;1<β≤2

(11)

LevyFlights的随机步长si,j可由下式得到

(12)

μ和v从以下正态分布中获得

μ～N(0,σμ2),v～N(0,σv2)

(13)

σμ，σv可由下式得到

(14)

式中，Γ为伽马函数.

随后，粒子将通过LevyFlights的随机步长si,j移动更新至下一个点：

xi,j(t+1)=xi,j(t)+si,j

(15)

在PSO-LF算法中，部分粒子采用LevyFlights的更新方式，能够平衡局部搜索及全局搜索的比例，提高搜索效率.群体粒子在解空间中进行更新时，部分粒子在最优值附近搜索，加快了局部更新速度；另外的粒子在距当前最优值较远的位置进行搜索，确保种群多样性，弥补了PSO算法易陷入局部最小值的不足.基于LevyFlights的PSO算法与群居动物的简化社会行为一致，在解决空间搜索问题上应用广泛，能得到高效的优化仿真结果.

2.3 改进的PSO算法在配网规划中的实现

据前文所述，将改进的PSO算法运用于配网规划中，其实现步骤如下：

步骤1 设定基本参数及系统约束.确定所采用的配网系统，输入配网系统参数；根据相关规定确定DG的个数及安装位置，输入DG参数；确定PSO-LF算法的最大迭代次数tmax,令迭代次数t=0，确定粒子个数、学习因子、惯性权重系数及退火常数，输入算法基本参数；确定节点电压、功率平衡及DG容量等约束，输入系统约束条件信息.

步骤2 随机初始化.群体粒子存在于一维空间中，粒子的位置xi定义为DG并网容量的大小，对群体粒子的位置xi和速度vi进行初始化，确定初代xi和vi.

步骤3 评价粒子适应度，确定初代最优.利用前推回代法进行潮流计算，计算目标函数值，评价群体粒子的适应度，确定初代pi和g.

步骤4PSO-LF算法在配网规划中的运用.利用随机函数rand产生0到1之间的随机数，如果随机函数rand<0.8，转步骤5，否则转步骤6.

步骤5 采用PSO算法的更新方式.用式(9)更新种群粒子的位置和速度.

步骤6 采用LevyFlights的更新方式.用式(15)更新种群粒子的位置和速度.

步骤7 更新pi.对比第t代各粒子位置的适应度与第t-1代pi中位置的适应度，若前者较好则更新pi.

步骤8 更新g.对比第t代pi与第t-1代g中位置的适应度，若前者较好则更新g.

步骤9 令t=t+1，当t=tmax+1时，算法运行tmax次，达到最大迭代次数，此时g中粒子的位置即为PSO-LF算法得到的最优位置也即此时DG并网最优容量，通过计算得到系统约束条件下的目标函数优化值，输出优化仿真结果，否则转步骤4.

PSO-LF算法流程图如图1所示.

图1 PSO-LF算法流程图

3 算例分析

本文采用33节点配网系统进行算例分析.该系统含33个节点，32条支路，基准值为SB=100MVA，UB=10kV，系统额定电压为12.66kV，系统总负荷为3715kW+j2300kvar.该系统是由JKLYJ-240架空线组成的单辐射网络，共四条分支，其中1-18分支为最长，最大线路传输容量为10.5MVA，配网网损率约为5%.

根据文献[9]的要求，10kV及以上电压等级的配网系统应接入容量为200kW以上的DG，同时限制DG并网容量不超过该并网节点的负荷容量[10]，因此，只能选择24,25,32号节点作为DG并网节点，且每个节点分别安放一个DG.因此，本文将三种类型的三个DG依次接入33节点配网系统，其中DG1为PQ型，DG2为PV型，DG3为PI型，图2为其系统拓扑图.

图2 含DG的33节点配网系统图

PSO-LF算法的基本参数设定：学习因子C1=C2=2.05；粒子个数为50；惯性权重系数w=0.5；退火常数为λ=0.5.在进行关于算法迭代次数的仿真试验时，观察到各目标函数在迭代到50次以内即可得到恒定的优化值，以此作为算法的收敛判据，同时确定算法最大迭代次数tmax=50，即该算法迭代50次得到的仿真结果即为最优结果.本文视上述三个单目标函数模型为同等重要，对各权重系数做等值处理，令w1=w2=w3=0.333.

下文将从DG并网前后配电网优化的比较、单目标与多目标优化的比较、算法改进前后优化的比较三方面进行算例分析.

3.1 DG并网前后配电网优化的比较

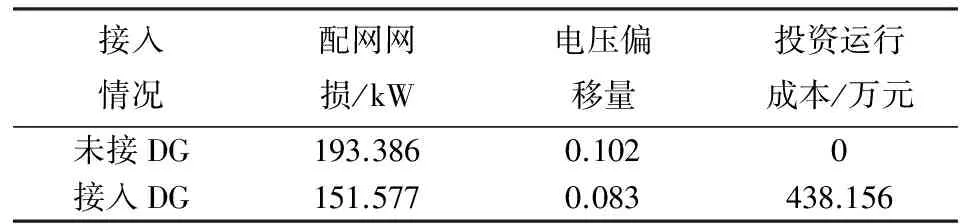
采用PSO算法对配网系统进行仿真，由表1可看出,DG并网之后，DG投资运行成本由0万元变为438.156万元，增加了配网运行成本；而配网网损及电压偏移量显著减少，分别减少了21.6%、18.6%，说明DG的合理配置对降低配网网损、降低电压偏移有一定的作用.

表1 基于PSO算法的DG并网前后的配电网单目标优化仿真结果

接入情况配网网损/kW电压偏移量投资运行成本/万元未接DG193．3860．1020接入DG151．5770．083438．156

3.2 单目标与多目标优化的比较

采用PSO-LF算法，首先对DG并网后的配网网损、电压偏移量、DG投资运行成本这三个目标函数进行优化，然后对归一化的多目标函数进行优化.优化仿真结果见表2、表3，可以看出，表2进行单目标优化，得到每个单目标函数的优化值、平均优化时间、DG1到DG3的并网容量；表3进行多目标优化，综合考虑三个指标，既可同时得到三个单目标函数的优化值，又可得到多目标函数的优化值、优化时间，还可得到DG并网容量，此容量为满足系统约束条件下的最优并网容量.多目标优化相较于单目标优化，大大缩短了优化时间，有效减少了配网网损、电压偏移量及DG投资运行成本.

表2 基于PSO-LF算法的单目标优化仿真结果

优化结果配网网损/kW电压偏移量DG投资运行成本/万元目标函数优化值135．5330．066382．853平均用时/s15．89317．93216．775DG1容量/kW350．874309．064245．776DG2容量/kW244．135299．923352．721DG3容量/kW202．337210．000207．855

表3 基于PSO-LF算法的同时考虑配网网损、电压偏移及DG投资运行成本的优化仿真结果

优化结果配网网损/kW电压偏移量投资运行成本/万元多目标函数/万元目标函数优化值122．7620．054337．862170．931平均用时/s13．791DG1容量/kW370．103DG2容量/kW329．256DG3容量/kW210．000

3.3 算法改进前后优化的比较

将PSO-LF及PSO两种算法进行对比，以验证前者的优越性.表4为PSO及PSO-LF算法的多目标优化仿真结果，由该表可知：采用PSO-LF算法，有效减小了配网网损、电压偏移量以及DG运行费用.图3为两种算法在电压偏移目标函数中的比较，由图可知，PSO算法收敛速度慢、不稳定、精度不高，易陷入局部最优，而PSO-LF算法收敛速度快且有效避免过早收敛，能及时跳出局部最小值.图4为第50次迭代后的33节点配网系统电压幅值的变化，可知PSO-LF算法改善了全网电压分布，降低了电压偏移，充分说明PSO-LF算法在解决DG并网的合理配置问题上是可行的，在求解复杂的多模态高维优化问题时是合理的.

表4 基于PSO及PSO-LF算法的同时考虑配网网损、电压偏移及DG投资运行成本的优化仿真结果

算法配网网损/kW电压偏移量投资运行成本/万元多目标函数/万元PSO137．9970．068371．113189．454PSO⁃LF122．7620．054337．862170．931

图3 PSO及PSO-LF算法在电压偏移目标函数中的比较

图4 PSO及PSO-LF算法在33节点配网系统中各节点电压的比较

4 结束语

综合考虑配电网实际运行约束条件，对含不同类型DG的配电网进行多目标优化，得到各目标函数值及DG并网的最优容量，充分说明DG并网的多目标优化对减少配网网损、DG并网成本以及降低电压偏移方面的重要意义.本文提出PSO-LF算法，改变了全局最优解的更新策略，提高了全局搜索效率.优化结果验证了PSO-LF算法收敛精度高，不易陷入局部最优，说明该算法是可行有效的.

[1]王瑶.分布式电源接入配电网的优化配置研究[D].昆明：昆明理工大学，2015.

[2]张君则.多类型分布式电源选址定容及其优化运行研究[D].北京：华北电力大学，2015.

[3]王园媛，秦文萍，李晓明.基于蚁群算法的多类型分布式电源优化配置[J].水电能源科学，2014，32(8)：161-164.

[4]庄园，王磊.分布式电源在配电网络中优化选址与定容的研究[J].电力系统保护与控制，2012,40(20)：73-78.

[5]THOMSON M，INFIELD D G. Network power-flow analysis for a high penetration of distributed generation[J]. IEEE Transactions on Power Systems，2007，22(3):1 157-1 162.

[6]卢扬，吴俊勇，郝亮亮.基于改进MOBPSO算法的含分布式电源的多目标配电网重构[J].电力系统保护与控制，2016，44(7)：62-68.

[7]刘会家，李奔，廖小兵，等.含分布式电源的配电网快速前推回代算法[J].水电能源科学，2016，34(6)：213-216.

[8]朱晓恩，郝欣，夏顺仁.基于Levy flight的特征选择算法[J].浙江大学学报(工学版)，2013,47(4):638-643.

[9]国家电网公司.Q/GDW 480-2010 分布式电源接入电网技术规定[S].北京：中国电力出版社，2011.

[10]李振.配电网中分布式电源的选址定容研究[D].南京：南京师范大学，2013.

(编辑：刘宝江)

Optimization of distribution network with distributed generation based on improved PSO algorithm

ZHANG Li-xin,LIU Wei

(School of Electrical and Electric Engineering,Shandong University of Technology, Zibo 255049, China)

Considering the operation constraints of the distribution network, a multi-objective optimal model is established by minimizing the loss of the distribution network, the voltage deviation and the DG investment operation costs. The PSO-LF algorithm is proposed to optimize the model. By using the update mechanism of Levy Flights, PSO-LF algorithm can improve the low efficiency of PSO algorithm and help jumping out of the local optimal particles. The simulation results of the 33 nodes distribution system show that the above-mentioned model is reasonable and the PSO-LF algorithm is feasible to solve the multi-objective optimization problems of the distribution network with DG.

distributed generation; distribution network; multi-objective optimization; PSO algorithm; Levy Flights

2016-11-29

张丽馨，女，18353359573@163.com； 通信作者： 刘伟，男，weikey@sdut.edu.cn

1672-6197(2017)06-0053-05

TM715

A