基于RASV模型和HMC算法的沪深300指数分析

李 荃，唐亚勇

(四川大学，四川 成都 610065)

基于RASV模型和HMC算法的沪深300指数分析

李 荃，唐亚勇

(四川大学，四川 成都 610065)

尝试使用Takahashietal．在2009年提出的RASV模型[1]，对沪深300指数的波动率进行建模分析。在确定模型参数时，使用贝叶斯统计推断，并创新性地使用结合了Gibbs抽样思想的HMC算法来模拟生成参数样本。使用的数据是2016年全年的沪深300指数一分钟高频数据，并对得到的模型参数进行了经济学意义分析。

RASV模型；贝叶斯统计推断；Gibbs抽样思想；HMC算法；沪深300指数波动率分析

一、引言

长期以来，对于波动率的估计一直都是众多研究者所密切关注的问题。由于波动性是金融市场最主要的特征之一，因此对于波动率动态的建模与分析等一系列工作变得日益重要，是进行资产定价、风险管理等金融行为的核心工作。

对于波动率的研究可以追溯到三十多年前，在那些年代，对于波动率的研究主要基于日收益率，比如GARCH模型或者SV模型。近年来，由于计算机技术的发展，日内高频收益率数据的获取变得很容易，因此研究者的目光逐渐转向如何利用日内高频收益率来对波动率进行估计。已实现波动率(Realized Volatility)就是其中一类重要研究方法。然而，由于非交易时间、微观市场噪声等因素的存在，已实现波动率对于真实波动率的估计仍存在一定的偏差，如何纠正这种偏差成为国内外研究者关注的热点问题。Takahashi et al．提出的基于SV模型的RASV模型为解决该问题提供了一种思路，该模型将日收益率和已实现波动率统一在一个模型中进行估计，尝试使用日收益率中蕴含的信息来纠正已实现波动率对真实波动率估计中的偏差。

如何对于SV类模型的参数进行有效的估计一直是一个难点问题，直到随着MCMC方法的提出和不断发展，Jacquier et al．(1994)将基于现代贝叶斯分析方法的MCMC方法引入了SV模型的参数估计中，从此MCMC方法成为研究者对于SV类模型的参数估计的主要方法[2]。此后，针对不同情况的参数估计，统计学家们开发了多类MCMC算法。其中Neal(2010)提出的HMC算法[3]利用了局部的几何结构采更快的生成建议值，对于高维分布的模拟效率有显著提高。

考虑到RASV模型中形式复杂的待估计参数，本文尝试在MH框架下结合Gibbs抽样和HMC算法，得到了适用于模拟复杂高维分布的Gibbs-HMC算法。利用Gibbs-HMC算法，对RASV模型的参数进行了模拟抽样。模拟次数为50000次，去掉10000次burn-in后，得到了40000个样本。本文将模拟抽样得到的样本的平均值作为参数估计值，并对参数估计结果做出了分析。分析结果表明，RASV模型可以比较准确的描述中国股市的统计特征。

二、RASV模型

Takahashi et al．于2009年提出了RASV模型，其核心思想是同时利用包含日内高频收益率数据信息的已实现波动率和日收益率数据来建立模型。利用日收益率中受微观市场噪音影响较小的真实波动率的潜在信息，校正己实现波动率的偏差，使得该模型对真实波动率的估计准确程度大大上升。同时，由于日收益率和已实现波动率在同一模型中的相互制约，使得研究者在使用该模型时无需额外地去计算最佳抽样频率。此外，该模型由于引进了日收益率的参数模型，最终除了得到一个真实波动率的估计之外，还可以得到日收益率的一个模拟分布，因此可以轻易地通过日收益率的模拟分布去计算VAR、预期短缺等常见金融风险测度量。

其统计结构如下所示：

y1，t=exp(ht/2)t，

t=1，2，…，T，

y2，t=ξ+ht+ut，

t=1，2，…，T，

ht+1=μ+φ(ht-μ)+ηt，

t=1，2，…，T，

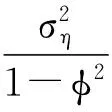
t=1，2，…，T.

其中y1，t是日收益率时间序列，y2，t则是已实现波动率序列。ht是潜在的真实波动率，参数μ表示其均值，可以衡量整个系统波动率的平均水平。参数φ则表示其一阶自相关性，用以刻画波动率的持续性效应。参数ξ是偏差校正项，用以校正已实现波动率对真实波动率估计的偏差。t、ut和ηt则是波动项，而参数ρ代表了y1，t与ht+1之间的波动相关性，用以刻画市场中可能存在的非对称效应。

三、对RASV模型的贝叶斯统计推断

贝叶斯统计推断是用以估计参数的常用方法。其基本思路是，假定要估计的模型参数是服从某一分布的随机变量，首先根据经验或者主观判断给出待估计参数的一个先验密度函数π(θ)，关于该先验分布的信息被称作先验信息：然后根据已知的样本信息给出的似然函数L(X|θ)，应用贝叶斯定理，得到待估计参数的后验密度函数P(θ|X)，进而得到后验分布。然后利用得到的后验分布的统计性质来估计参数。贝叶斯统计推断通常结合MCMC方法使用，使用MCMC方法可以由后验密度函数直接模拟得到一个符合后验分布的参数样本，然后利用模拟得到的样本的性质来估计模型参数。

为了贝叶斯统计推断时的便利性，本文首先对RASV模型进行等价变形，主要是对真实波动率做一个中心化的处理，然后将波动项标准化。

令σ=exp(μ/2),αt=ht-μ,c=ξ+μ，则 RASV模型的等价形式为：

y1，t=σexp(αt/2)t，

t=1，2，…，T，

y2，t=c+αt+σuut，

t=1，2，…，T，

αt+1=φαt+σηηt，

t=1，2，…，T，

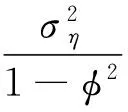
t=1，2，…，T.

接下来对上述形式的RASC模型进行贝叶斯统计推断。

首先凭经验给出参数θ1=(c,σu,σ,φ,ση,ρ)的先验分布：

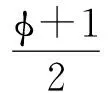
由此可以得到θ1的先验密度函数：

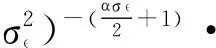
而α=(α1，α2，α3，…，αT)的先验密度函数

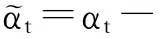
接下来计算θ1和α的似然函数L(θ1,α|y1，y2)

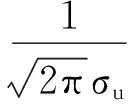
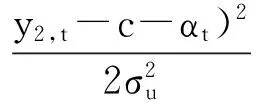
由上可以计算θ1和α的后验密度函数，本文给出的是其对数形式：lnP(θ1,α|y1,y2) =lnp(θ1,α)+lnL(θ1,α|y1,t,y2,t)

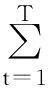
四、Gibbs-HMC算法

在t时刻，θ(t)=θ，设θ=(θd1,θd2,…θdk)，结合Gibbs抽样的HMC算法(Gibbs-HMC)生成θ(t+1)时依次更新θd1,θd2,…θdk，同时每步更新都引入一个随机变量p，其中更新θdi的步骤为：

·生成随机数p～N(0,Indi)，V～π(θdi|θ-di),r=1,其中ndi是θdi的维数，且

θ-d1=(θd2,θd3,…θdk)

θ-di=(θd1,…θdi-1,θdi+1…θdk),i=2,3…k

·依据以下映射生成建议值：

Τdi:[θ，V，p，r]→[ξ，W，p′，r′]

其中由于HMC中每一步Metropolis更新包含L步广义leapfrog迭代，设映射Τdi表示包含一步广文leapfrog迭代的更新：

Tdi:[θ，V，p，r]→[ξ，W，p′，r′]

ξ-di=θ-di

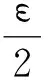
W=θdi

r′=-r

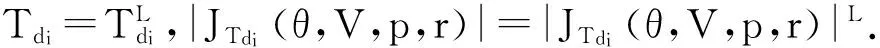
·计算接受概率：

其中|JTdi(θdi,V)|是映射Tdi的雅可比行列式在(θdi,V)点处的取值。由于Gibbs抽样和HMC算法中的映射都是自逆的，因此映射Tdi作为这两者的复合映射也是自逆的，所以|JTdi(θ，V，p，r)|=1。

同时有

π(ξ,W,p′) =π(ξdi,p′|ξ-di,W)π(ξ-di,W)

=π(ξdi,p′|θ-di,θdi)π(θ-di,θdi)

=π(ξdi,p′|θ)π(θ)

=π(ξdi,p′|π(θ)

π(θ,V,p) =π(V,p|θ)π(θ)

=π(V,p)π(θ)

于是有接受概率

=min{1,exp[H(V,p)-H(ξdi,p′)]}

五、实证分析

(一)数据处理

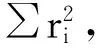
(二)应用Gibbs-HMC算法

设θ1=(c,σu,σ,φ,ση,ρ)，为了应用Gibbs-HMC算法对θ=(θ1,α)的联合后验分布进行模拟抽样，我们首先把随机向量θ分为5部分，即θ=(α,φ,(σ,ση,ρ),σu,c)，设θ(1)=α，θ(2)=φ，θ(3)=(σ,ση,ρ)，θ(4)=σu,θ(5)=c，然后依次更新θ(1)，θ(2)，…θ(5)。

(三)参数估计结果

将处理过的沪深300指数数据代入RASV模型，然后对其参数的后验密度函数应用Gibbs-HMC算法。对参数进行了50000次模拟，去掉10000次burn-in，每个参数均得到40000个样本。

参数c，σu,σ,φ,ση,ρ的样本频数直方图见图(1)

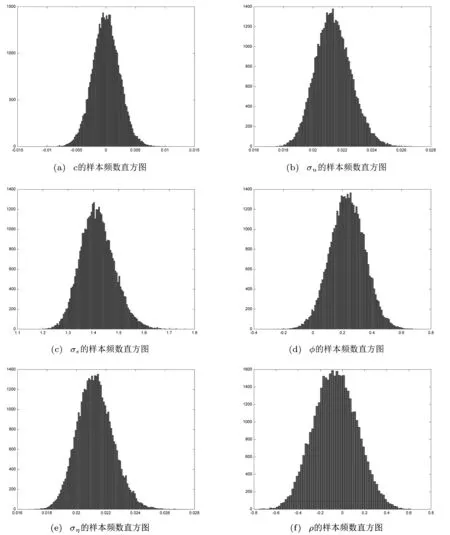
图1

取得到的参数样本的均值作为估计值，如(表1)所示。

表1

(四)参数样本的生成效率检验

首先，还是计算生成的参数样本的自相关系数，考察其收敛性。

α，c，σu，σ，φ，ση，ρ的1000阶自相关系数如下图所示(2)：

从下图中可以看出，生成的样本，自相关系数下降同样非常迅速，表明Markov链收敛到目标分布的收敛速度比较快。

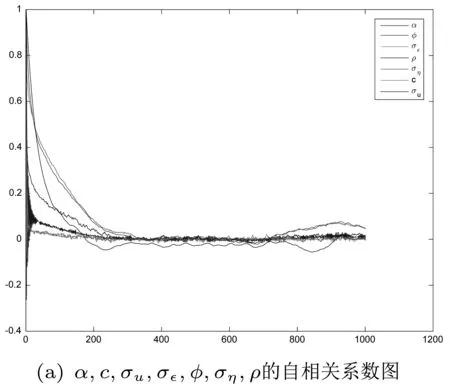
图2

同样的，我们继续计算样本的无效因子IP值，IP取值越小样本的有效性越强。

计算α，c，σu，σ，φ，ση，ρ的10000阶无效因子IF，结果如图(3)所示。

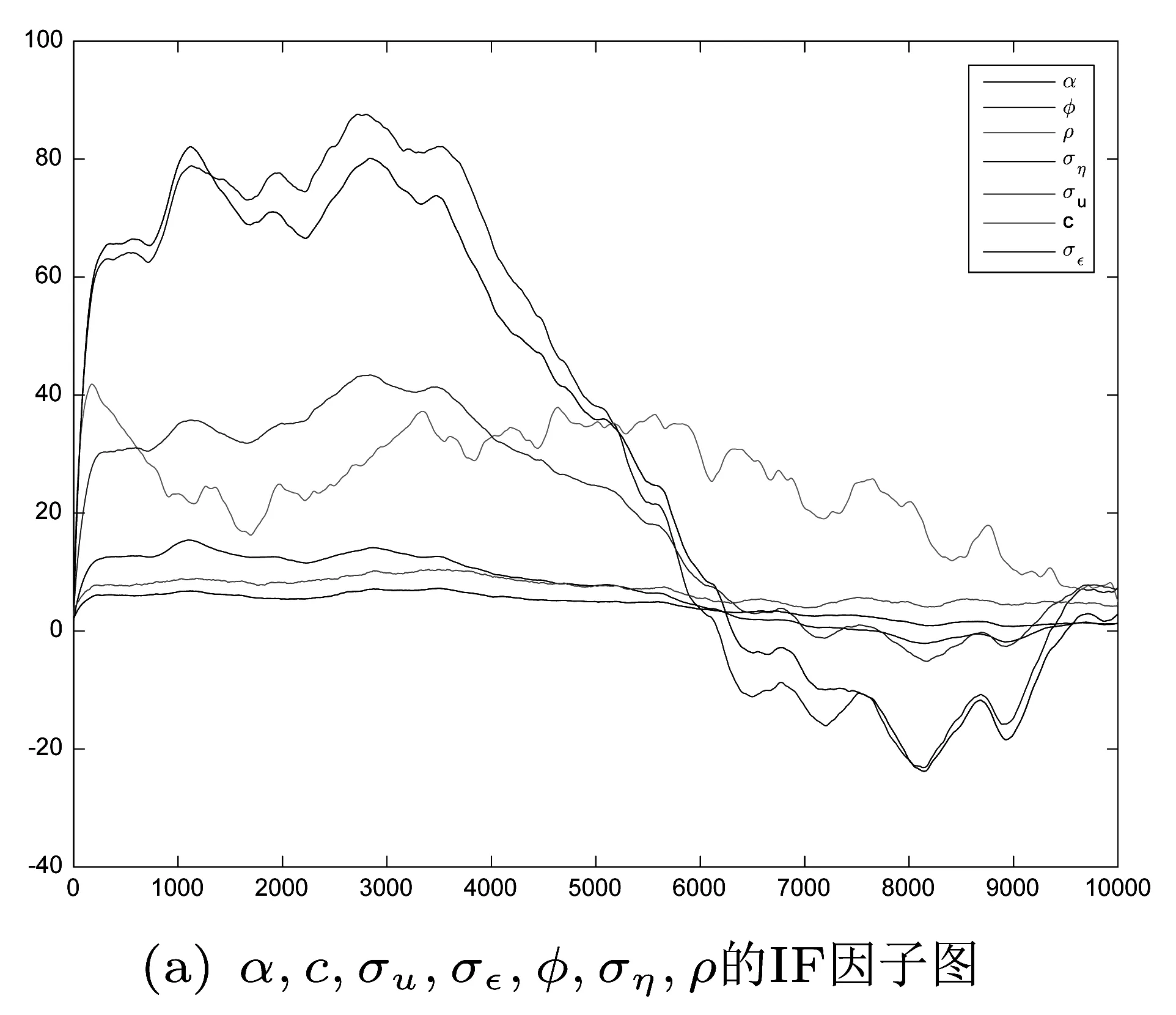
图3

可以看出，φ和ση的无效因子IF值开始较高，但最终在接近10000阶时都稳定在了0附近，说明生成的样本的有效性比较高。

(五)参数估计结果分析

参数的估计值θ′，如下表所示(表2)。

表2

由σ=exp(μ/2)，c=ξ+μ，可以反解出μ和ξ。

μ=2lnσ，

ξ=c-μ.

计算可得μ的估计值为-0.921，ξ的估计值为0.953。因此，可以得到变形前的RASV模型的参数估计值，如下表所示(表3)：

表3

其中，参数ξ的估计值反映的是沪深300指数数据中，微观市场噪声和非交易时间对已实现波动估计真实波动率时的影响。由于ξ的估计值0.953>0，说明日内1分钟高频数据得到的已实现波动率对真实波动率来说是一个偏高估计。这表明在2016年的沪深300股票市场中，已实现波动率对真实波动率估计的偏差主要来源于微观市场噪声的影响，而非非交易时间的影响，而参数ση的估计值表明了已实现波动率对真实波动率估计的扰动水平，其值为0.57。

参数μ的估计值为-0.921，反映的是沪深300指数波动率的波动水平。参数φ的估计值反映的则是波动率的持续性参数，由于其估计值0.369较高，可以看出我国2016年的股市具有较强的波动持续性。参数σu的估计值表明了沪深300指数波动率的扰动水平，其值为0.894。

参数ρ的估计值则反映了y1，t与ht+1之间的相关性。其估计值-0.052<0，说明t日收益率与t+1日的波动率之间是负相关的，因此证明我国2016年股票市场上存在非对称效应。

六、结论

本文使用了2016年1月1日至2016年12月31日的沪深300指数数据，利用RASV模型对我国股市的收益率特征进行建模模拟，其中已实现波动率数据使用了该时段的1分钟高频数据。随后使用Gibbs-HMC算法对RASV模型的参数进行了模拟抽样，模拟次数为50000次，去掉10000次burn-in后，得到了40000个样本。最后，将模拟抽样得到的样本的平均值作为参数估计值，并对参数估计结果做出了分析。分析结果表明，RASV模型可以比较准确的描述中国股市的统计特征。

[1]Takahashi M，Omori Y，Watanabe T，(2009)．Estimating stochastic volatility models using daily returns and realized volatility simultaneously．Comput Stat Data Anal 53：2404-2426.

[2]Jacquier，E.，Polson，N．G.，Rossi，P．E．(1994)．Bayesianan alysis of stochastic volatility models(with discussion)．J．Business Econom．Statist．12，371-417．

[3]Neal，R．M．(2010)．MCMC using Hamiltonian dynamics．In Handbook of Markov Chain Monte Carlo(eds S．Brooks，A．Gelman，G．Jones and X．-L．Meng)．BocaRaton：Chapman and Hall-CRC Press．

2017-05-20

李荃(1993-)，男，山东滨州人，四川大学数学硕士，从事MCMC算法及其应用研究。 唐亚勇(1974-)，男，四川成都人，博士，副教授，硕士研究生导师，主要研究方向为金融数学及应用统计学。

O24

A

1008—3340(2017)03—0084—05