带有交叉扩散项的反应扩散系统的 Turing 不稳定性

徐 瑞，田美美，徐衍聪

(杭州师范大学理学院，浙江 杭州 310036)

带有交叉扩散项的反应扩散系统的 Turing 不稳定性

徐 瑞，田美美，徐衍聪

(杭州师范大学理学院，浙江 杭州 310036)

通过研究含有 Lotka-Volterra 捕食和被捕食动力学行为的反应扩散方程的交叉扩散项来解释斑图的形成机制. 借此来说明能导致部分斑图出现的交叉耗散项在失稳机制中的重要性.在稳定区域的附近采用弱非线性分析方法来研究斑图的振幅， 得到其 Stuart-Landau 规范型振幅方程. 最后，当斑图作为行波的波前侵入区域时，可以得到 Ginzburg-Landau 规范型振幅方程，这一方程常常用来研究波的形状和波速.

交叉耗散；Turing 不稳定；振幅方程；五次 Stuart-Landau 方程；Ginzburg-Landau 方程

1 预备知识

斑图动力学是非线性科学领域内的一类重要的分支.作为一门应用科学，它的研究内容广泛地涉及物理学、力学、化学、生物学、生态学等各方面. 斑图(Pattern)是在空间和时间上具有某种规律性的非均匀宏观结构.它普遍存在于自然界中，形形色色的斑图结构构成了多姿多彩、千姿百态的世界. 因而越来越多的人将目光转向生物学领域，并用一个反应扩散模型成功地解释某些生物的体表所显现的图纹，如斑马身上的斑纹形成机理.

文章的主要目的在于研究下列反应扩散系统的斑图形成过程：

(1)

这里的U(z,τ) 和V(z,τ)，z∈Ω⊆Rn分别是捕食者和被捕食者的种群密度,R和K分别是捕食者的增长率和捕捉能力，M是被捕食者的死亡率，γ12和γ21分别是捕食和捕获效率并且Γ 是空间区域的大小. 两个种群的空间运动是由简单线性耗散项和源于假设有高密度的捕食者区域的非线性项来描述的.通过无量纲化，把系统 (1) 化为关于变量u和v的系统：

(2)

这里有

(3)

和

(4)

以下的讨论限制在一维空间Ω=[0,2π]上并运用齐次Neumann边值条件讨论以上系统.系统(2)是依赖于扩散项[1]和交叉耗散项来产生分离影响和空间生态位的一类模型[2-4].交叉扩散项是用来引入说明一类种群的密度梯度来减少另一类种群的变迁情形.这就是说，对于一大类捕食-被捕食或竞争动力学没有自动催化项的系统来看，无论扩散率是多少，经典的扩散项的扩散都是不能充分揭示斑图的形成原因：在这些情况下，交叉扩散被用来解释斑图形成机理[3,5-6].值得一提的是，交叉扩散项的引入是可以严格地通过锚定到微观世界的自相一致推导得到[7]，或从单一品种的变异和分裂推导[8-9].系统(2)中介绍该类型的交叉扩散方面已经在文[3,10-11]出现，但是在其他方面比如趋化[12]、生态学[13]、社会系统[14]、电子电路[15]、半导体中的漂移扩散[16]、化学反应[17]、等离子体中的湍流[2]、粒状材料[18]和细胞分裂的肿瘤生长[19]都已经被广泛地通过数值计算进行过研究[20-22].

第二部分，采用线性稳定性分析研究共存奇点的动力学行为，表明交叉扩散是斑图形成的重要原因之一.第三部分，通过弱非线性分析，得到三次Stuart-Landau规范型振幅方程(但是，在次临界区域，必须得到五次Staurt-Landau规范型振幅方程来研究)，以此预测形状和图案的振幅.在次临界区域，那里的线性分析没有时间的振荡规定而只有Turing模式，并且发现了数字并存与极限环图灵模式.这些发现同样证实了这一结果，即使是没有Hopf分支或波不稳定,Turing不稳定性与交叉扩散的捕食模型也可以产生时空振荡的解[23-24].在文[25-26]中也发现了振荡图灵斑图的类似模型.最后，第四部分，在空间域很大的情况下考虑空间调制斑图，即波前解的存在性，并且这些斑图模式是有次序地侵入到整个区域.

2 Turing 不稳定

在本节中, 将研究系统 (2) 的 Turing 不稳定性.易知该系统的共存非边界平衡点是(u0,v0)≡(1,r-γ), 这一平衡点当且仅当r-γ>0 时才具有生物学意义. 当它存在时, 平衡点是稳定的, 可以是一个有吸引力的节点(当 0γ+γ2/4). 显然，此时该系统不会出现 Hopf 分支.因此考虑在(u0,v0) 附近线性化该系统:

(5)

这里有

(6)

给出特征值为波数的函数色散关系如下：

(7)

这里有

(8)

不失一般性，文中假设 det(D)>0.

静态状况下的线性不稳定的空间扰动要求对于k≠0 有R(λ(k))>0.由于(u0,v0) 在动力学上是稳定的，故有 tr(J)<0, 而且tr(D)>0.因此，寻找这些当h(k2)<0 情况下的k值.若式(8)有正实部的特征根，需保证其系数异号，而此时，唯一的可能性是当h(k2)<0 时q<0，即

(9)

因此，当线性扩散项起稳定作用的时候，唯一的潜在不稳定机制是交叉扩散项的存在.令d=d21-d12，在k=kc临界条件是

(10)

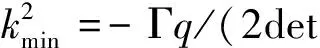
(11)

对应的临界波数是

(12)

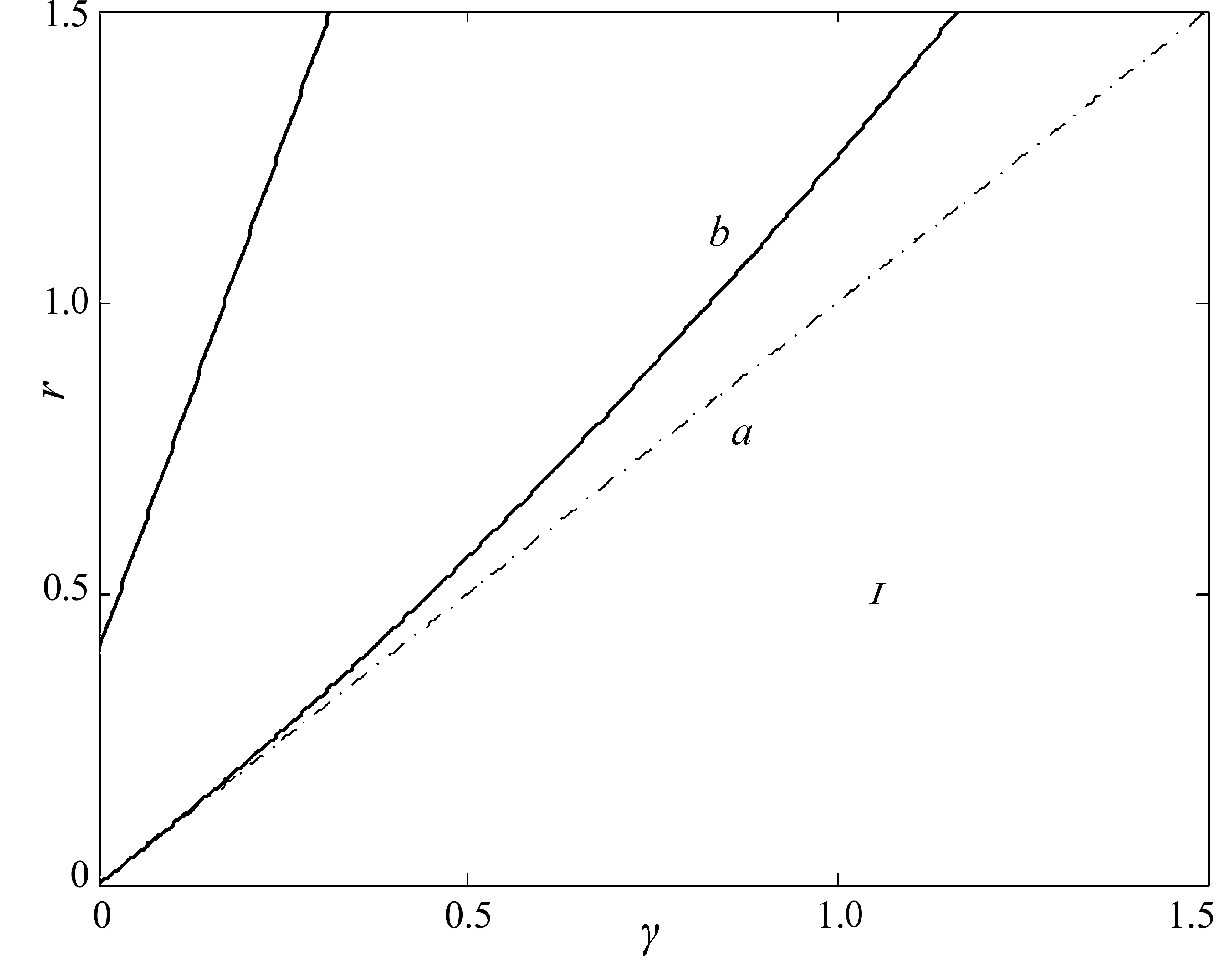
图1 当r>γ时的Turing不稳定区域Fig.1 The region for Turing instability as r>γ

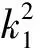
(13)

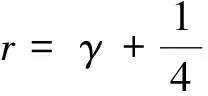
3 弱非线性分析

在本节中，将对系统(2)应用多尺度方法进行弱非线性分析.取ε2=(d-dc)/dc为无量纲化的距离阈值(threshold).为简便起见，这部分用d1代替d12、d2代替d21.

首先，引入新的尺度变换：

(14)

因此偏导数 ∂t→∂t+ε2∂T和 ∂x→∂x+ε∂X作为振荡振幅的时间尺度和空间尺度来解耦，在这个阶段，暂时忽略空间调制缓慢的可能性，这将在第五部分考虑.

分离系统的线性与非线性部分后，改写带有扰动w=(wu,wv) 的系统(2)为如下形式：

(15)

这里有一个依赖于分支参数d的线性算子Ld=ΓJ+Dd2和一个双线性算子 Qk，这里的， Qk代表了系统的非线性部分，定义为:

其中x=(xu,xv) 和y=(yu,yv).最后，公式(15)的最后两项是非线性扩散项.

按下列方式展开d1、d2和w:

因此，线性算子Ld和 Qk可以被展开为：

这里Ldc=ΓJ+Ddc2，且.将上述的展开式分别代入式(15)中并收集ε的各次项，则可以得到一系列关于wi的方程.

在O(ε) 次项中，得到线性问题Ldcw1=0，它的解满足 Neumann 边值条件，则有

由于Ldc不作用慢尺度T上，因此这里的A(T) 是在这个水平上的任意斑图的振幅. 向量ρ=(ρu,ρv) 定义到一个常数，并且能够按下列方式规范化：

(16)

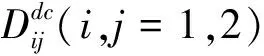
在O(ε2) 次项中，得到下列系统：

(17)

通过 Fredholm 更替原理，方程(17)有解当且仅当=0，这里的·,·是在L2(0,2π/kc) 下的标量积，且，因此

(18)

因此 Fredholm 更替条件自动满足.因此，对于线性部分，方程 (17) 得到一下满足 Neumann 边界条件的解:

这里的w2i(i=0,2) 是下列线性系统的解：

(19)

(20)

在O(ε3) 次项中得到：

(21)

这里有

因此，根据方程 (21) 的可解性条件，得到 Stuart-Landau 规范型振幅方程：

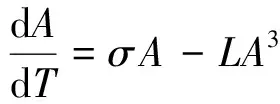
(22)

这里的系数σ和L如下：

(23)

如果d>dc，斑图在此参数区域内可形成. 容易证明系数σ总是正的.另一方面， Landau 常数L可以是正的或者负的，这取决于系统参数的值.因此 Stuart-Landau 的动力学行为可以被分为两种性质不同的情况： 超临界情况(L>0)，次临界情况(L<0). 而L作为所有参数的函数.

3.1 超临界状态

如果方程 (22) 系数σ和L都是正的，则出现超临界分支. 在这种情况下 Stuart-Landau 方程的静态平衡点是A并且解的时间渐近行为由下列方程给出:

(24)

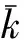
3.2 次临界状态

当L<0 时，系统出现次临界分支，在这种情况下，弱非线性展开式必须推高到五阶.因此，引入了多个时间尺度T和T1, 令

取时间导数解耦为 ∂t→∂t+ε2∂T+ε4∂T1+…， 并将d1、d2和w展开直到ε的五次项.

将展开式代入方程(15)，直到O(ε3)，将会得到和第三部分一样的方程.在O(ε3) 项，对式(21)利用可解条件=0 同样可以得到振幅方程(22)，尽管这里T的导数是偏导数.如果满足，则解是

这里w3i(i=1,2,3) 分别是下列线性系统的解：

在O(ε4) 次项：

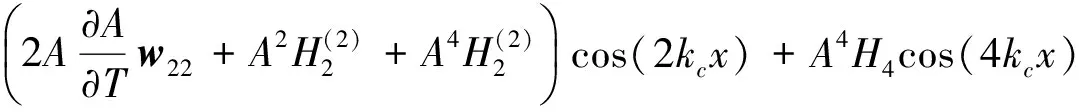
(25)

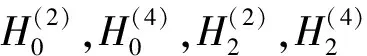
这里的w4i(i=0,…,4) 可由下列线性系统解得：

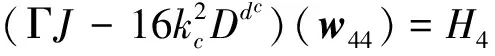
在O(ε5) 次项可得

(26)

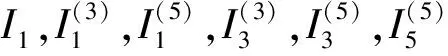
(27)

这里的系数分别是：

最后将式(22)加到式(27)，得到五次 Stuart-Landau 规范型振幅方程：

(28)

其中的系数分别是：

(29)

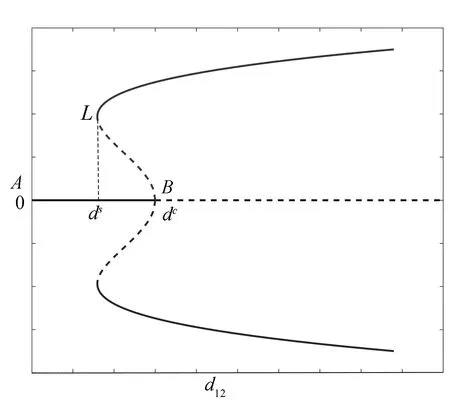
图2 次临界状态下的分支图Fig.2 Bifurcation diagram for subcritical state as <0

4 波 前

当物理区域很大时，斑图会连续地形成并以一种波前的状态侵入到整个区域. 为了描述这一现象，不得不考虑调制空间相关性的快慢程度，引入了弱非线性分析中定义的缓慢的空间尺度 (在式(14)中已有定义).随后一个确定性的算子就出现在式(15)中.在O(ε) 中，得到线性算子Ldcw1=0，这里的Ldc=ΓJ+Dd∂xx是线性算子的快部分算子.它的解是

这里的ρ由式(16)给出，A和前面的一样仍然是任意的.

在O(ε2) 次项中，得到方程

并且可解性条件自动满足，因此它的解是

这里的w2i(i=0,2)和wX1是下列线性系统的解：

在O(ε3) 次项中，可以得到：

利用可解条件得到关于振幅A(X,T) 的实 Ginzburg-Laudau 规范型振幅方程如下：

这里的σ和L由式(23)给出，耗散系数v的关系式如下：

这里的Ψ 由式(18)给出，(·,·) 是标准的标量积. 实 Ginzburg-Laudau 方程描述整个区域的入侵模式，并且它的解是一个斑图的包络解.

5 结 论

通过线性稳定性分析和弱非线性分析来说明交叉扩散是斑图形成的必要成分，进而说明即使是没有 Hopf 分支不稳定或Turing 不稳定，该模型同样可以产生时空振荡的解.从本文看，引入对偶的交叉扩散项，对 Turing 分支没有明显的影响，但是会影响 Turing 斑图发生的参数区域. 但实际上，加入对偶扩散项后，除了共存的3个奇点外，新的系统产生了至少2个新的奇点，这也说明对偶扩散项对系统的动力学行为的影响是显而易见的， 限于本文的研究内容，我们暂时不予研究， 将在随后的工作中刻画这2个新奇点引发系统产生的动力学行为.

[1] MULONE G, RIONERO S, WANG W. The effect of density-dependent dispersal on the stability of populations[J]. Fuel & Energy Abstracts, 2011, 74(74):4831-4846.

[2] DEL-CASTILLO-NEGRETE D, CARRERAS B A, LYNCH V. Front propagation and segregation in a reaction-diffusion model with cross-diffusion[J]. Physica D Nonlinear Phenomena, 2002,168-169(2):45-60.

[3] PENG R, WANG M, YANG G. Stationary patterns of the Holling-Tanner prey-predator model with diffusion and cross-diffusion[J]. Applied Mathematics & Computation, 2008, 196(2):570-577.

[4] SHIGESADA N, KAWASAKI K, TERAMOTO E. Spatial segregation of interacting species[J]. Journal of Theoretical Biology, 1979, 79(1):83-99.

[5] GAMBINO G, LOMBARDO M C, SAMMARTINO M. Turing instability and traveling fronts for a nonlinear reaction-diffusion system with cross-diffusion[J]. Mathematics & Computers in Simulation, 2012, 82(6):1112-1132.

[6] GAMBINO G, LOMBARDO M C, SAMMARTINO M. Pattern formation driven by cross-diffusion in a 2D domain[J]. Nonlinear Analysis-Real World Applications, 2013, 14(3): 1755-1779.

[7] FANELLI D, CIANCI C, PATTI F D. Turing instabilities in reaction-diffusion systems with cross diffusion[J]. The European Physical Journal B, 2013, 86(4):1-8.

[8] CONFORTO F, DESVILLETTES L. Rigorous passage to the limit in a system of reaction-diffusion equations towards a system including cross diffusions[J]. Communications in Mathematical Sciences, 2014, 12(3):457-472.

[9] GALIANO G. On a cross-diffusion population model deduced from mutation and splitting of a single species[J]. Computers & Mathematics with Applications, 2012, 64(6):1927-1936.

[10] DUBEY B, DAS B, HUSSAIN J. A predator-prey interaction model with self and cross-diffusion[J]. Ecological Modelling, 2001, 141(1):67-76.

[11] KUTO K, YAMADA Y. Multiple coexistence states for a prey-predator system with cross-diffusion[J]. Journal of Differential Equations, 2004, 197(2):315-348.

[12] KELLER E F, SEGEL L A. Model for chemotaxis.[J]. Journal of Theoretical Biology, 1971, 30(2):225-234.

[13] GILAD E, VON H J, PROVENZALE A, et al. A mathematical model of plants as ecosystem engineers[J]. Journal of Theoretical Biology, 2007, 244(4):680-691.

[14] EPSTEIN J M. Nonlinear dynamics, mathematical biology and social science[M]. Reading:Addison-Wesley, 1997.

[15] BILOTTA E, PANTANO P, STRANGES F. A gallery of Chua attractors: Part II[J]. International Journal of Bifurcation & Chaos, 2007, 17(2):293-380.

[16] LI C, ANSGAR J. Analysis of a parabolic cross-diffusion semiconductor model with electron-hole scattering[J]. Communications in Partial Differential Equations, 2007, 32(1):127-148.

[17] GAMBINO G, LOMBARDO M C, SAMMARTINO M, et al. Turing pattern formation in the Brusselator system with nonlinear diffusion[J]. Physical Review E, 2013, 88(1):042925.

[18] ARANSON I S, TSIMRING L S. Continuum theory of partially fluidized granular flows[J]. Physical Review E, 2001, 65(1):061303.

[19] SHERRATT J A. Wavefront propagation in a competition equation with a new motility term modelling contact inhibition between cell populations[J]. Proceedings of the Royal Society A, 2000, 456:2365-2386.

[20] BARRETT J W, BLOWEY J F. Finite element approximation of a nonlinear cross-diffusion population model[J]. Numerische Mathematik, 2004, 98(2):195-221.

[21] GALIANO G, GARZN M L, JÜNGEL A. Semi-discretization in time and numerical convergence of solutions of a nonlinear cross-diffusion population model[J]. Numerische Mathematik, 2003, 93(4):655-673.

[22] GAMBINO G, LOMBARDO M C, SAMMARTINO M. A velocity-diffusion method for a Lotka-Volterra system with nonlinear cross and self-diffusion[J]. Applied Numerical Mathematics, 2009, 59(5):1059-1074.

[23] MADZVAMUSE A, NDAKWO H S, BARREIRA R. Cross-diffusion-driven instability for reaction-diffusion systems: analysis and simulations[J]. Journal of Mathematical Biology, 2015, 70(4):709-743.

[24] LI A W, JIN Z, LI L, et al. Emergence of oscillatory Turing patterns induced by cross diffusion in a predator-prey system[J]. International Journal of Modern Physics B, 2012, 26(31):3847-3856.

[26] TULUMELLO E, LOMBARDO M C, SAMMARTINO M. Cross-diffusion driven instability in a predator-prey system with cross-diffusion[J]. Acta Applicandae Mathematicae, 2014, 132(1):621-633.

Turing Instability in a Predator-prey System with Cross-diffusion

XU Rui, TIAN Meimei, XU Yancong

(School of Science, Hangzhou Normal University, Hangzhou 310036, China)

The pattern formation system was explained by studying the cross-diffusion in a reaction-diffusion system with Lotka-Volterra predator-prey kinetics. It was indicated that the cross-diffusion term that leads to the emergence of spatial patterns is responsible of the destabilizing mechanism. The amplitude of patterns were studied by weakly nonlinear analysis near marginal stability, and the Stuart-Landau amplitude equation was obtained. Finally, when the patterns invaded the domain as a travelling wavefront, the Ginzburg-Landau amplitude equation which was able to describe the shape and speed of the wave was derived.

cross-diffusion; Turing instability; amplitude equation, Quintic Stuart-Landau equation; Ginzburg-Landau equation.

2017-03-20

国家自然科学基金项目 (11671114); 杭州师范大学科研基金项目 (HNUEYT) .

徐衍聪(1970—)，男，教授，博士，主要从事微分动力系统分支研究. E-mail：yancongx@163.com

10.3969/j.issn.1674-232X.2017.04.004

O175.29 MSC2010:35K57；37L15

A

1674-232X(2017)04-0360-08