由聚氧乙烯和聚4‴-酰胺基对四联苯-2,6-二甲酰对苯二胺构筑的OAO形三元嵌段共聚物在N、N-二甲基甲酰胺中的自组装结构模拟

吴红枚 ，李永成，赵 耀，王 孟，王榆元

(南华大学化学化工学院高分子材料与工程系，湖南 衡阳 421001)

科研与开发

由聚氧乙烯和聚4‴-酰胺基对四联苯-2,6-二甲酰对苯二胺构筑的OAO形三元嵌段共聚物在N、N-二甲基甲酰胺中的自组装结构模拟

吴红枚 ，李永成，赵 耀，王 孟，王榆元

(南华大学化学化工学院高分子材料与工程系，湖南 衡阳 421001)

利用耗散粒子动力学模拟方法，研究了由拉胀聚合物聚4‴-酰胺基对四联苯-2,6-二甲酰对苯二胺(A)与聚氧乙烯(PEO)组成的OAO形三元嵌段共聚物在溶剂N、N-二甲基甲酰胺(DMF)中的自组装行为，探究了共聚物浓度和链段A的长度对三元嵌段共聚物自组装结构的影响。结果表明，由聚4‴-酰胺基对四联苯-2,6-二甲酰对苯二胺(A)与聚氧乙烯(PEO)构筑的线型嵌段共聚物在溶剂N、N-二甲基甲酰胺(DMF)中的自组装将形成形态各异的球状、柱状、毛刷型以及“球刺”状胶束等结构；随着共聚物浓度的增加，球状胶束结构消失，逐渐演变为柱状以及毛刷型结构；随着链段A长度的增加，共聚物形成的球状胶束结构慢慢转变为"球刺"状胶束。

耗散粒子动力学；聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺；聚氧乙烯；嵌段共聚物；自组装

一般认为，自然界中大部分材料的泊松比都为正值，即材料在受到拉伸时，材料的横向将发生收缩。拉胀材料[1]，则与之相反，具有负泊松比效应，即受到拉伸时，材料的横向将发生膨胀，而受到压缩时，材料横向将发生收缩。这一奇特的性质现在受到越来越多跨学科的研究者的关注和重视。

拉胀高分子材料是拉胀材料家族中最重要的一个分支。关于拉胀高分子的研究目前主要集中在两个方向，一个是通过对现有材料的再次加工使得原本不具有拉胀性的材料获得拉胀性，另一个方向则是基于获得分子水平上的拉胀性这一角度出发来设计、开发和制备全新的具有拉胀性的聚合物。到目前为止，前一方向上的进展较多，已经有拉胀聚氨酯[2]、拉胀聚四氟乙烯[3]和拉胀超高分子量聚乙烯[4]等品种的报道。而在后一方向，则以计算机模拟和分子设计方面的报道居多，有拉胀苯乙炔网络[5]，拉胀聚丁二炔链网络[6]，拉胀液晶高分子[7-8]，拉胀聚三角炔网络[9]，拉胀氢键自组装高分子[10-11]和拉胀聚酰胺类聚合物[12]等的报道。这些已经报道的品种都具有分子水平上的固有拉胀性，问题在于，其中一些品种的合成极其困难至今未见有报道[5-6，9]，另外一些品种虽然它们的合成有一些进展[7-8，13]，但要么未有完整的泊松比数据[7-8]，要么合成工作尚未完善[11]，而且虽然它们都具有分子水平上的固有拉胀性，但都是局限于在分子水平上的设计或计算。对于现实中的聚合物体系来说，还涉及到加工过程中的高级结构的形成过程，聚合物的结构层次也绝不是仅仅简单地局限于分子水平上的一级结构，而是一个多层次多尺度的结构。

因此，在本文中，我们选取了一个理论上具有分子水平拉胀性的聚合物，即聚4‴-酰胺基对四联苯-2,6-二甲酰对苯二胺作为代表，采用耗散粒子动力学的方法尝试研究在介观尺度的水平上，该拉胀聚合物与PEO所构建的OAO形三元嵌段共聚物在自身理论上的良溶剂作用下的自组装行为，探究聚合物浓度以及链段长度等因素对其自组装结构演变规律的影响。

本文将DPD方法应用于拉胀共聚物在溶液中自组装的研究，有助于深入理解由拉胀基元与柔性基元所构筑的嵌段共聚物在介观水平上的自组装结构与相行为。

1 研究方法与模型构建

1.1 研究方法

耗散粒子动力学方法，是上世纪90年代初由Hoogerbrugge和koelman[14]发展起来的一种介观计算机模拟方法。DPD体系中，基本的单位是一些离散的被称为“珠子”(bead)或者“粒子”(particle)的动量载体，它们代表着真实体系中的原子或者原子簇，是一个抽象的质点，每个珠子的质量为单位质量1，其运动遵循牛顿定律，具体表达式如下：

(1)

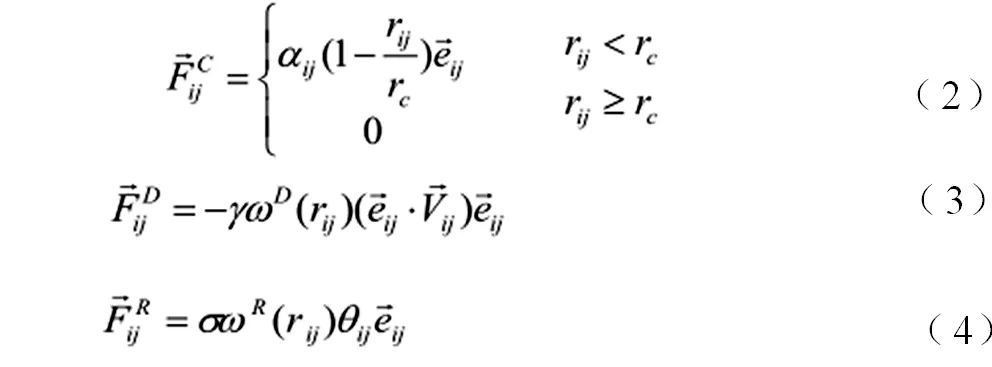
这三种力共同作用于每个珠子，从而影响珠子碰撞的结果。其中，为i粒子和j粒子之间的相互作用参数，也就是最大排斥相互作用， rc为相互作用截断半径，且，保守力是一种软作用力，体现了微观粒子局域的相互作用信息，包括键相互作用(键伸缩振动势、键角弯曲振动势、二面角扭转势以及交叉项)和非键相互作用(通常包括库仑相互作用和范德华相互作用等)，所以，在耗散粒子动力学中核心的问题就是保守力与微观系统性质之间的映射关系，如何确定DPD粒子间相互作用势，使其能够正确反映特定粗粒化级别粒子间相互作用的本质，在本文所使用的DPD模拟方法中，利用Groot和Warren[15]建立的DPD与Florry-Huggins理论之间的联系，来确定的值：

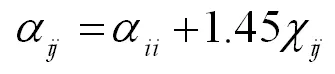
(5)

而耗散力和随机力分别起着消耗和补偿系统能量的作用， ωD和ωR是两个依赖于r的权重函数，分别描述了耗散力与随机力随粒子间距离增加而衰减的情况， γ和σ两个系数分别来描述随机力和耗散力的大小。Espanol和Warren[16]认为，耗散力和随机力必须遵循耗散-涨落定理，体系才符合正则平衡分布，即满足以下关系：

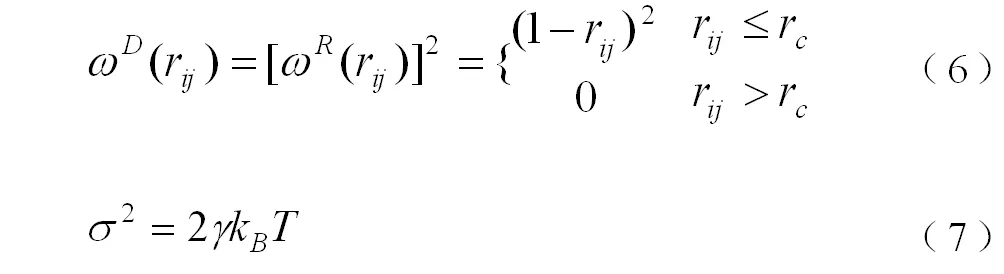
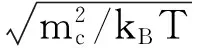
DPD方法仍然属于动力学模拟方法，动力学模拟中的一个中心问题就是如何对体系的运动方程进行积分。目前，最常用的方法是Groot和Warren提出的改进的Velocity-Verlet算法，它考虑到了耗散力与速度的相互依赖关系，在积分过程中加入一个可调参数 λ，利用粒子当前的位置、速度和力来计算下一个时刻的位置和速度，然后再用新的位置和速度计算新的力，进而修正速度，每运行一步，力就更新一次，占用的计算机内存并不多。具体的积分方法如下：

合适的 λ可以使得体系的能量飘逸降到最低，但是它的取值取决于其他模型参数，是具有经验性的，一般λ取为0.65。

另外，当DPD方法应用于高分子体系研究时，对于高分子链，除上述作用力之外，相邻链节间还需引入连接作用力，如弹簧力，可表示为：

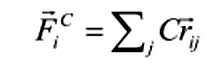
(8)

式中，C为链中粒子之间的弹性常数。

1.2 模型构建

我们选取聚4′′′-酰胺基对四联苯-2,6,-二甲酰对苯二胺为线型芳酰胺聚合物的典型代表，其结构如图1所示。对以该聚合物(Auxetic polymer，A)与聚氧乙烯(poly(ethylene oxide)，PEO)为嵌段，所构筑的OAO形三元嵌段共聚物OYAXOY在溶剂DMF中的自组装行为进行模拟研究，这里用A代表聚4′′′-酰胺基对四联苯-2,6,-二甲酰对苯二胺，O代表PEO，下标x、y分别代表对应的粗粒化粒子的数目，所构建的线型嵌段共聚物模型示意图如图2所示。

要建立一个粗粒化模型，需要确定模拟珠子的体积。每个不同的珠子代表一定数量的单体单元或溶剂分子簇，并且拥有相同的体积，这样能保证Florry-Huggins理论和DPD方法可以联系起来。通过Gaussian 09软件计算可以得到PEO重复单元，DMF单个分子以及线性芳酰胺重复单元的体积，其值分别为65Å3，100Å3，1342Å3，在模型中，用粗粒化粒子A，O以及S来分别代表芳酰胺嵌段，PEO嵌段以及溶剂分子DMF。在本文的模拟工作中，我们以1个芳酰胺重复单元定为一个粗粒化粒子A，以此推算，一个体积相当的粗粒化粒子O相当于20个PEO的重复单元，同样，一个体积相当的粗粒化粒子S包含了13个DMF分子。

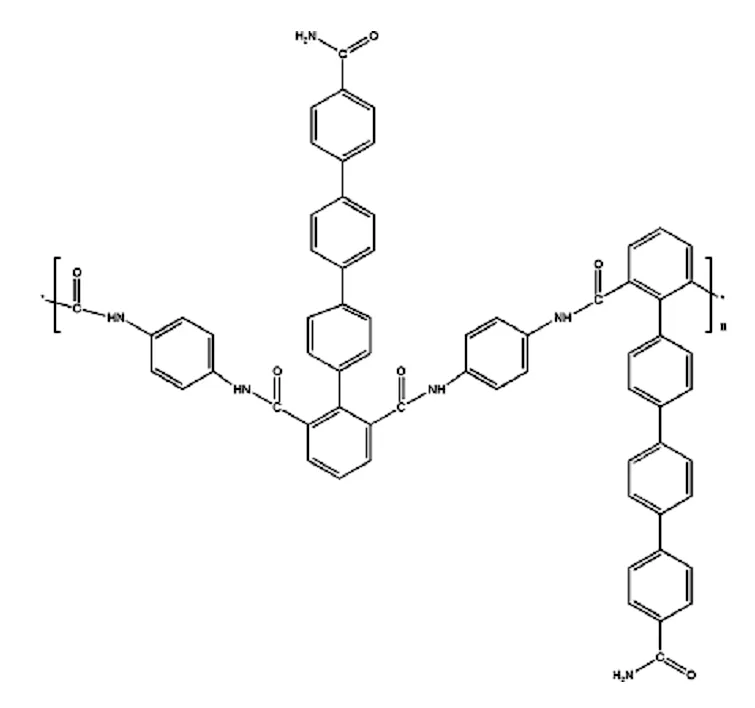
图1 聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺的结构

A：Auxetic Polymer O：PEO

我们需要确定的是粗粒化粒子间的相互作用参数。对于相同粒子间的相互作用参数，由于我们所取的体系粒子密度为ρ=3，则取αii=25，而不同粒子间的相互作用可以利用Groot和Warren建立的DPD与Florry-Huggins理论之间的联系(公式4-1)，确定αij的值。可以由以下公式得到：

(9)

式中，Vbead是体系中粗粒化粒子的体积，δi和δj是i粒子和j粒子的溶度参数，我们按照付一正[17]等人的方案，模拟计算得到。计算得到的Florry-huggins参数和相互作用参数 如表1所示。

表1 模拟中使用的相互作用参数

(b) DPD输入参数αij

2 结果与讨论

2.1 共聚物浓度的影响

在这一部分，探讨了自组装过程中聚合物浓度对线型嵌段共聚物在DMF中自组装结构的影响。以O4A4O4组成的嵌段聚合物为例，用φp代表共聚物的浓度，分别设定φp=0.05, φp=0.1, φp=0.15, φp =0.2以及φp=0.3，对这些不同浓度的嵌段聚合物在DMF中的自组装进行了耗散粒子动力学模拟。模拟所得到的结构如图3所示(为了清晰，未显示溶剂分子的图像)。其中，绿色粒子代表链段A(即聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺)，红色粒子代表链段O(即PEO)。可以看到，在聚合物浓度比较小(φp=0.05)的时候，聚合物自组装形成的聚集体是以A为核，O为壳的球状胶束结构，随着聚合物浓度的增加，聚集体逐渐由球状胶束结构继续聚集，转变为更大的球形胶束结构(φp=0.1和φp=0.15)。φp进一步增大时，聚集体逐渐转变成柱状胶束结构(φp=0.2)和毛刷型结构(φp=0.3)。这些结构的形成是聚合物-溶剂之间的界面能和柔性链段O和刚性的聚合物链段A之间的弹性拉伸势能共同作用的结果。

为了更好地描述上述自组装结构，我们计算了O粒子以及A粒子在X方向上的数密度分布，计算结果如图4所示。可以明显地看到，随着φp的增大，粒子密度分布出现了明显的不同。

(a)φp =0.05;(b) φp =0.1;(c) φp =0.15;(d) φp =0.2;(e) φp =0.3

(a) φp =0.05;(b) φp =0.1;(c) φp =0.15;(d) φp =0.2;(e) φp =0.3

2.2 链段A长度的影响

在这部分工作中，讨论了当固定共聚物的浓度为φp=0.05时，随着链段A长度的增加，嵌段共聚物的自组装结构的变化。固定链段O的长度为4，将链段A的长度增加，得到的自组装结构如图5所示(为了清晰，未显示溶剂分子的图像)。其中，绿色粒子代表链段A(聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺)，红色粒子代表链段O(即PEO)。图5的结果显示，当A嵌段的长度为4时，此时体系的自组装形成的是球形胶束结构，当A嵌段的长度增加到6个粒子时，体系自组装形成的依然是球状胶束，不过链段A长度为6的时候有向更小球状胶束转变的趋势；但当A嵌段的长度增加到8时，体系形成了哑铃型的胶束结构；当A嵌段的长度增加10和12时，整个体系形成了一种由刚硬链段彼此相连的鸟窝形骨架"刺"所支撑的软链段团聚的小球状胶束，而相比A嵌段的长度为10的球状胶束，A嵌段长度为12的球状胶束更大，数目更少。

上述自组装结构的各粒子的数密度分布图如图6所示，从图5和图6可以看出，当A嵌段长度为4、6和8的时候，聚合物形成的聚合体是以A为核，O为壳的结构；当A嵌段为10和12的时候，聚合物形成的聚合体是以O为核，A为壳的"刺"状球型结构，这很好地反映了共聚物的结构。与图6(a)、图6(b)和图6(c)中的结构不同，从图6(d)和图6(e)中我们可以发现粒子A的密度大于粒子O的密度，链段A组成的"刺"状外壳形成了类似鸟窝的骨架结构。

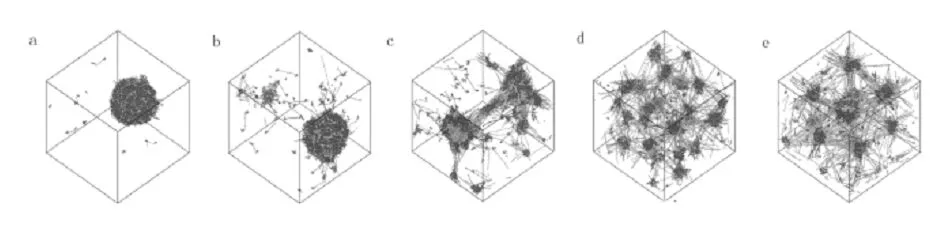
(a)O4A4O4;(b) O4A6O4;(c)O4A8O4;(d) O4A10O4(e) O4A12O4

(a)O4A4O4;(b) O4A6O4;(c)O4A8O4;(d) O4A10O4(e) O4A12O4

3 结论

通过对拉胀聚合物聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺进行耗散粒子动力学模拟，分析了聚合物浓度，链段长度对自组装结构的影响。结果表明，线型嵌段共聚物会在溶液中自组装形成球状、柱状、毛刷型以及"球刺"状胶束等结构；随着共聚物浓度的增加，球状胶束结构消失，逐渐演变为柱状以及毛刷型结构；随着链段A长度的增加，共聚物形成的球状胶束结构慢慢转变为“球刺”状胶束。

本论文首次尝试将DPD方法应用于拉胀共聚物在溶液中自组装结构形态的研究，模拟的结果显示在介观水平上拉胀共聚物在溶液中的形态事实上是非常丰富的，这一结果也揭示从分子水平上的拉胀性到宏观水平上的拉胀性之间可能因为结构上的多样性因而并非呈现一一对应的关系。

致谢：感谢合作单位东华大学材料科学与工程学院提供的软件支持。

[1] 魏 荣, 吴红枚, 李 竞,等. 拉胀高分子材料的研究进展[J]. 高分子材料科学与工程, 2013(1):183-186.

[2] Lakes R. Foam structures with a negative poisson's ratio[J]. Science, 1987, 235(4792):1038-1040.

[3] Caddock B D, Evans K E. Microporous materials with negative poisson's ratios. I. microstructure and mechanical properties[J]. Phys D: Appl Phys, 2000, 22(12):1877-1882.

[4] Alderson K L, Evans K E. The fabrication of microporous polyethylene having a negative Poisson's ratio[J]. Polymer, 1992, 33(20):4435-4438.

[5] Evans K E, Nkansah M A, Hutchinson I J. Molecular network design[J]. Nature, 1991, 353(6340):124.

[6] Baughman R H, Galvao D S. Crystalline networks with unusual predicted mechanical and thermal properties[J]. Nature,1993, 365(6448):735-737.

[7] Ren W, Mcmullan P J, Griffin A C. Stress-strain behavior in main chain liquid crystalline elastomers: effect of crosslinking density and transverse rod incorporation on "Poisson's ratio"[J]. Phys. Status, 2009, 246(9):2124-2130.

[8] 李晨光, 基于液晶共聚酯的拉胀高分子材料的设计与合成[M]. 郑州:郑州大学, 2000.

[9] Grima J N, Farrugia P S, Gatt R, et al. Connected triangles exhibiting negative poisson's ratios and negative thermal expansion[J]. Phys Soc Jpn, 2007, 76(2):5001.

[10] 吴红枚, 魏高原. 几种自组装拉胀分子网络的分子模拟[J]. 高分子学报, 2004(2):201-207.

[11] 吴 斌, 赵 耀, 吴红枚,等. 线形芳酰胺聚合物的力学性能模拟[J]. 南华大学学报(自然科学版), 2014(4):86-90.

[12] 赵 耀, 吴红枚, 黄慧君,等. 聚多联苯2,6-二甲酰对苯二胺的力学性能模拟[J]. 高等学校化学学报, 2015, 36(7):1416-1421.

[13] 吴红枚，吴 斌，王榆元,等. 2,4′′,6-三酰胺基三联苯及其制备方法和应用:CN,201410130953.X[P].2014-04-02.

[14] Hoogerbrugge P J, Koelman J M V A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics[J].Euro phy Lett, 1992, 19(3): 155-160.

[15] Groot R D, Warren P B. Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation[J]. Chem Phy, 1997, 107(11):4423-4435.

[16] Espanol P, Warren P B. Statistical mechanics of dissipative particle dynamics[J].Euro phys Lett,1995, 30:191.

[17] 付一政, 刘亚青, 兰艳花. 端羟基聚丁二烯/增塑剂共混物相容性的分子动力学模拟[J]. 物理化学学报, 2009, 25(7):1267-1272.

(本文文献格式：吴红枚 ，李永成，赵 耀，等.由聚氧乙烯和聚4′′′-酰胺基对四联苯-2,6-二甲酰对苯二胺构筑的OAO形三元嵌段共聚物在N、N-二甲基甲酰胺中的自组装结构模拟[J].山东化工，2017，46(06)：1-4.)

Simulation of Self-assembly of OAO-type Triblock Copolymers Constructed from Polyethylene oxide and Poly (p-phenylenediamine-4‴-aminocarbonyl-alt-2,6 -diformyl quaterphenyl) in N,N-Dimethylformamide Using Dissipative Particle Dynamics Method

WuHongmei*,LiYongcheng，ZhaoYao，WangMeng，WangYuyuan

(Department of Polymer Science and Engineering, College of Chemistry and Chemical Engineering, University of South, Hengyang 421001, China )

Dissipative particle dynamics(DPD)simulation was employed to examine the self-assembly behavior of linear triblock copolymers which are constructed of poly(ethylene oxide) (PEO) and Poly (p-phenylenediamine-4‴-aminocarbonyl-alt-2,6-diformyl quaterphenyl) (A) in N,N-Dimethylformamide (DMF). In this paper, we focused on the relationships between the evolution of self-assembly structure of those copolymers in DMF with increasing of the concentration of copolymers and the length of block A ,respectively. Simulations show that the self-assembly of those linear block copolymers in DMF can form various structures with different shapes such as spherical, cylindrical, brush type, and spiny ball shape micelles. With increasing concentration of copolymer, the self assembly structure will develop from spherical micelle to cylindrical micelle and then turn into brush type micelle. While with increasing length of block A, the self assembly structure will develop from spherical micelle to spiny ball shape micelle under certain concentration of copolymer.

dissipative particle dynamics；polyethylene oxide；poly (p-phenylenediamine-4‴-aminocarbonyl-alt-2,6 -diformyl quaterphenyl)；block copolymer；self-assembly

2017-02-14

国家自然科学基资助项目(21104031)

吴红枚(1975—)，女，湖南平江人，副教授，硕士生导师，主要从事高分子材料的研究。

O631.4

A

1008-021X(2017)06-0001-04