基于双因素Wang转换方法的长寿风险债券定价研究
樊 毅,张 宁,王耀中
(1.中南林业科技大学 经济学院,湖南 长沙 410004;2.湖南大学 经济与贸易学院,湖南 长沙 410079;3.湖南大学 金融与统计学院,湖南 长沙 410079)*
·金融与保险·
基于双因素Wang转换方法的长寿风险债券定价研究
樊 毅1,2,张 宁3,王耀中2
(1.中南林业科技大学 经济学院,湖南 长沙 410004;2.湖南大学 经济与贸易学院,湖南 长沙 410079;3.湖南大学 金融与统计学院,湖南 长沙 410079)*
在比较国外经典债券设计的基础上,基于离散型死亡率模型假设,设计一种可调整上触碰点的触发型长寿债券,运用带永久跳跃的APC模型和双因素Wang转换定价方法对长寿债券进行定价,实证结果表明:在不同的参数组合下的风险溢价均处在一个合理的范围,由于模型参数多、可用死亡率数据年限短,风险溢价的结果对无风险利率等参数敏感性较高。
长寿风险债券;双因素Wang转换;死亡率;定价
一、引 言
近年来,长寿风险日益严峻,学者们不断寻求和探索新的风险管理方式,并将目光集中在发达的资本市场,于是,死亡率风险证券化越来越受到关注和重视。长寿债券是一种本金或未来息票给付依赖于生存者指数的债券。不少学者对长寿债券的设计与定价进行了研究,死亡率风险证券化的概念首次在Samuel H.Cox(1998)的演讲中被提出;Blake和Burrows(2001)认为可以运用长寿债券来规避长寿风险,首次提出了基于生存概率连续性支付票息的长寿债券[1]。在风险定价方面,Wang分别于2000年和2002年在金融风险和保险风险的定价上推广运用概率分布扭曲方法[2,3]。Bauer(2010)等通过比较分析Wang转换和其他定价方法,发现Wang转换定价方法较其它方法更优[4]。Wang转换方法通过长寿风险市场价格这一参数,将实际生存率转换成风险调整后的生存率,然后用无风险利率进行贴现,从而得到长寿风险证券的公允价值[5,6]。Lin和Cox(2005)将Wang转换方法运用在长寿债券的定价上,测算得出长寿债券的市场价格[7]。在过去的几十年里,保险公司成功地将财产保险巨灾风险通过发行巨灾债券的方式转移至金融市场[8,9]。
目前,众多死亡率债券和长寿债券被设计出来并在资本市场上发行。国内方面,谢世清(2014)采用风险中性的定价方法,推导得出长寿债券的定价解析式[10]。尚勤和秦学志设计了一种长寿债券,运用Wang转换定价方法对该债券进行定价,并使用我国经验数据进行了实证研究[11,12]。胡仕强(2015)利用Lee-Carter模型和Wang转换方法,基于中国人口死亡率预测数据对长寿连接型债券进行了定价尝试[13]。尚勤(2010)从投资者视角对欧洲投资银行(EIB)和法国巴黎银行(BNP)在2004年联合发行的长寿债券从息票支付、违约风险、风险承担机制以及模型参数的不确定性等方面进行深入剖析,分析了该债券发行失败的原因[14]。国内外发行长寿债券以连续型为主,死亡率模型的使用也大多是连续型的。本文将基于离散型死亡率模型假设,设计一种可调整上触碰点的触发型长寿债券,运用带永久跳跃的APC模型和双因素Wang转换定价方法对长寿债券进行定价。
二、本金在险型长寿债券的设计思路
(一)国际经典死亡率债券的实践
国际经典死亡率关联债券以2003年瑞士再保险公司(Swiss Re)发行的死亡率债券和2004年欧洲投资银行(EIB)发行的长寿债券为代表。
Swiss Re于2003年12月发行了为期三年的死亡率巨灾债券,到期日为2007年1月1日,用来转移Swiss Re巨灾事件的死亡率风险,这是世界上第一支死亡率债券,是寿险风险证券化史上具有开创意义的尝试。该债券的面值为4亿美元,投资者按季度获得的息票设置为3个月美元LIBOR加135个基本点。本金则是无保证的,其返还依赖于五国(美国、英国、法国、意大利和瑞士)的死亡率指数。当实际死亡率指数不超过2002年基准水平的1.3倍时,本金全额返还;死亡率指数每增加0.01,本金返还减少5%;当死亡率指数超过基准水平的1.5倍时,无本金返还。瑞士再保险公司建立了一个名为Vita Capital Ltd.的特殊目的的机构(Special Purpose Vehicle,简称SPV),该死亡率债券由Vita Capital发行,Swiss Re支付保费给Vita Capital,Vita Capital在资本市场发行债券获取4亿美元的本金,并每季支付一次利息给债券投资者。本金返还率公式表示如下:
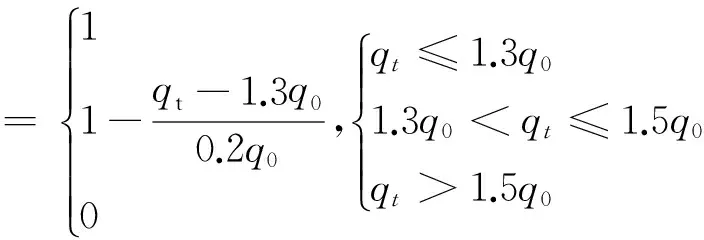
(1)
式(1)中,q0为2002年死亡率指数;qt分别代表2004年、2005年和2006年的实际死亡率,该死亡率由美国、英国、法国、意大利和瑞士等五国人口死亡率按一定权重比例决定。Beelders和Colarossi(2004)用极值理论对该债券进行估值,对死亡率进行广义帕累托分布假设[15]。Beelders和Colarossi通过计算,预测死亡率指数超过130%的可能性在33个基本点,而大于150%的机率在15个基本点,期望损失最高在22个基本点,这大大低于债券定价中支付给投资者的135个基本点,因此,该债券被认为对投资者十分有利。从市场反应来看,投资者对这种债券的确表现出极大的兴趣,对债券的主要投资人(年金基金机构)来说,该债券既提供了高利息收入,又是一个有丰厚回报的对冲长寿风险的工具,其发行取得了巨大的成功。具体结构关系如图1所示。
随后,第一次真正尝试长寿风险证券化的是2004年11月由法国巴黎银行(BNP,Business News publishing)设计、欧洲投资银行(European Investment Bank,EIB)发行的长寿债券。为了转移养老金和年金保险人的长寿风险,2004年11月,欧洲投资银行(EIB)发行了一支初始本金为5.4亿英镑,期限为25年的长寿债券。该债券与Blake和Burrows在2001年提出的经典生存债券较为相似。该债券的设计可以帮助年金计划者对冲长寿风险,利息的支付与生存者指数挂钩,生存者指数的计算基于英国政府精算署(GAD)公布的2002年65岁威尔士和英格兰男性群体实际死亡率而确定。最初的利息支付额设定为0.5亿英镑,目标群体是英国养老金基金的投资者,债券由Partner Re进行了再保险。遗憾的是,由于没有足够的市场需求,该债券在投入市场一年后被撤回。众多学者讨论了该债券发行失败的原因主要有以下几点:一是债券设计上存在缺陷,其中最突出的是存在巨大的基差风险;二是该债券具有资本要求高而风险降低少的特点,且未考虑通货膨胀因素,这使其需要占用投资机构大量资本,也使得该债券成为一种昂贵的债券;三是债券透明度不高,缺乏灵活性、投资者对长寿风险不熟悉等[16]。

图1 Swiss Re 2003年发行的死亡率债券结构图来源:根据Cowley和Cummins (2005) 资料整理。
(二)本金在险型长寿债券的设计
长寿债券的类型总的说来可以分为两大类:一是本金有风险的长寿债券。当相关的死亡率事件发生时,债券持有者可能会丧失全部或部分本金,Swiss Re死亡率债券为该类型。二是利息有风险的长寿债券(EIB/BNP长寿债券属此类型)。息票的支付随死亡率波动而变化,息票具体的变化方式又可分为利息支付是死亡率指数的连续函数(即连续型)和投资者因死亡率指数超过某一约定数值而损失的部分乃至全部利息(即触发型)两种。另外也有少数本金和利息均在险的债券类型。
不同长寿债券的构造方式不同,但它们都存在一个负责设计、发行长寿债券的特殊目的的机构(SPV)。SPV是一个以资产证券化为唯一目的的独立法律实体,在整个资产证券化操作流程中处于核心地位。通过设立SPV,实现了资产与发起人的有效隔离,它不仅是发起人和投资者之间的中介,还连接着受托管理机构、评级机构、担保机构和证券承销商等中介服务机构。SPV是资产证券化交易结构的核心和中枢。寿险公司或年金公司支付固定费用给SPV,SPV按照事先约定的死亡率指数发生情况向其支付浮动的金额,同时SPV向投资者发行债券,募得本金,定期支付给投资者固定或浮动的息票,期满按照合同约定的死亡率发生情况部分或全部返还本金给投资者。SPV现金流如图2所示。

图2 SPV现金流图资料来源:作者整理。
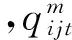
(2)

(3)
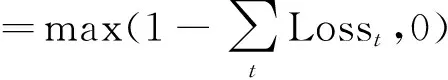
式(3)中,U是预先设定的生存者指数的最高触碰点,L是最低触碰点,Ut=min(Ut-1,St-1)。本金返还比例依赖于对中国2004—2018年死亡率的预测。 当生存者指数超过U时,本金全额返还;当生存者指数低于L时,则无本金返还。
设定L=0.6S0,U=0.9S0,S0=q0=0.00844是2003年的生存者指数。将下触碰点固定为0.6S0,上触碰点根据实际情况作出调整,比如从0.9S0调整到0.85S0,甚至0.8S0。该债券可用图3表示。

图3 长寿债券示意图
三、带永久跳跃的APC死亡率模型假设
长寿风险源于人口寿命不可预期的变化,通常用死亡率和生存率来衡量长寿风险。传统的静态死亡率模型主要用于对死亡率经验数据的拟合,一般较少用来预测死亡率。随着学者们对死亡率模型研究的逐渐深入,人们开始认识到时间变化对死亡率有重要影响,从而涌现出一批随机动态死亡率模型。
(一)Age-Period-Cohort(APC)模型
在随机模型中,影响力最大、运用最广泛的是Lee-Carter模型,随后很多学者都致力于对Lee-Carter模型进行扩展与改进。Lee-Carter(1992)初始模型如下[17]:
logm(x,t)=αx+βxkt
(4)
其中,m(x,t)为x岁的人在t时刻的中心死亡率,αx表示x岁的人死亡率对数的平均值;kt反映死亡率随时间的变化趋势;βx表示各年龄人群的死亡率对时间因子kt的敏感程度。时间因子kt通常服从带漂移的一维随机游走过程和ARIMA过程。
Lee-Carter模型的最主要特点是简单易运用,另外它也能得到比较准确的死亡率预测结果,所以被广泛运用于死亡率预测的研究中。最近几年,学者们在不断改进初始Lee-Carter模型的过程中,一系列Lee-Carter类模型被提出来,如Renshaw和Haberman(2003)模型[18]:
(5)
与死亡率相关的不仅有年龄和时间,还有出生年代效应,Renshaw和Haberman(2006)率先提出了带有出生年效应的随机动态死亡率模型[19]:
(6)
其中参数γt-x表示出生年效应,用来反映出生年t-x对死亡率的影响,虽然模型(6)对历史数据拟合较好,但是稳定性不够。于是Cairns等(2008)指出,当改变拟合模型的年龄范围时,参数估计值就相应出现较大区别,并通过进一步的研究发现,模型稳健性与似然函数的形状关系密切[20]。
Currie于2006年给出了模型(6)的精简形式,即Age-Period-Cohort模型(APC模型)。APC模型对美国历史数据有较高的拟合检验,同时还避免了模型(6)中出现的参数估计稳健性问题[21-23]。
logm(x,t)=αx+kt+γt-x
(7)
樊毅(2017年)运用中国人口死亡率数据,对Lee-Carter、APC等八个随机死亡率模型进行了比较分析,结果表明,APC模型对中国全年龄人口数据的拟合效果和预测效果也是最优的。因此,本文在长寿债券定价时,选用APC模型作为死亡率假设的基本模型①。
(二)带跳跃的APC模型
Lee和Carter(1992)用一维带漂移项的随机游走过程描述了时间效应kt。
kt+1=kt+μ+σZt+1
(8)
式(8)中,σ表示常数波动率,Zt+1表示一维独立同分布的标准正态分布N (0, 1),μ为常数漂移项。
死亡率风险证券化或长寿风险证券化的目的是用来对冲极端死亡率风险或长寿风险。在风险证券化过程中,由于极端事件导致死亡率的跳跃是一个需要考虑的因素,但现有很多研究都忽视了极端死亡率的跳跃过程,如Lee和Carter(1992)、Li和Chan(2007)在研究中将流行疾病等极端事件视为一种干扰,从而将其影响从模型中移除出去[24]。当前研究中,极少文献在死亡率风险证券化建模过程中考虑了死亡率的跳跃情况。
Cox等(2006)结合几何布朗运动和复合泊松过程,提出了连续时间下永久跳跃的死亡率模型[25],Chen和Cox(2009)在此基础上又给出了离散时间下的永久跳跃过程[26]。
kt+1=kt+μ-pm+σZt+1+Yt+1Nt+1
(9)
式(9)中,Yt+1代表t+1年发生跳跃的严重程度的独立同分布正态变量,该变量均值为m,标准差为s;Nt+1表示第t+1年发生跳跃的频率数,且独立于Yt+1。为简单起见,假定发生跳跃的次数N在某一年内最多为一次,且概率为p,N要么在概率p下取值为1,要么在概率1-p下取值为0。

(10)
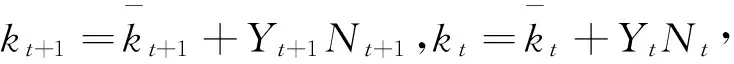
kt+1=kt+μ+σZt+1+Yt+1Nt+1-YtNt
(11)
Chen和Cox(2009)使用美国1900—2003年不同年龄段的死亡率数据计算瞬时跳跃、永久跳跃和没有跳跃三种情况下kt模型的拟合参数,结果表明,在似然比检验下,带跳跃的死亡率模型比不带跳跃的死亡率模型拟合效果更好,而带瞬时跳跃的模型比带永久跳跃的模型更加适合死亡率风险证券化。
长寿市场上的投资者主要关注的是不可预期的死亡率改善状况,这点与死亡率证券化会有很大不同。比如研发成功一种新药可以治愈某种癌症,那么,死亡率会有一个较大程度的下降,并且这种死亡率改善情况将会永久持续下去。因此,带永久跳跃效应的死亡率模型更适合应用于长寿风险证券化中。考虑到中国人口可得数据的年限较短,对加入永久跳跃后的时间因子kt模型参数估计非常困难,所以,本文借鉴Chen和Cox(2009)的研究结果来确定定价过程中死亡率模型的时间因子kt的参数值,如表1所示。

表1 带永久跳跃的kt模型的参数估计值
资料来源:Chen和Cox(2009)。
本文获取的原始数据来源于1995—2014年的《中国人口统计年鉴》与《中国2010年人口普查资料》,选取1994—2013各年度的综合死亡人数和综合平均死亡风险暴露人数数据,总计20年。以0~89岁的人作为研究对象,采取单一年龄的死亡数据,年龄上限为89岁。
四、双因素Wang转换方法和定价过程
(一)双因素Wang转换方法
Wang(2000)运用损失超越曲线来描述巨灾债券所承担的损失,即巨灾产生的损失额X超过x的概率,其概率表达式为S(x)=Pr(X>x),并在此基础上提出单因素Wang转换的变形公式[27]:
S*(x)=Φ[Φ-1(S(x))+λ]
(12)
其中,Φ是标准正态分布的分布函数。对于一个给定的损失超越曲线S(x),单因素Wang转换的目的就是通过产生一条经过变换后的损失超越曲线S*对风险进行调整。也就是说,Wang转换后的分布函数隐含了风险附加,参数λ就代表风险溢价。另外,Wang转换对原有分布进行了风险调整,并且假如原分布S服从正态分布,那么,经过Wang转换后的分布S*也服从正态分布,即μ*=μ+δλ,δ*=δ。
上述Wang转换是假定风险的概率分布S(x)是已知的,但实际上只能在有限的数据基础上去估计概率分布,所以,就存在参数的不确定性问题。
Wang(2004)运用t分布替代具有未知参数的标准正态分布,并通过下式对经验估计的S(x)进行参数不确定性调整[28]:
S*(x)=Q[Φ-1(S(x))]
(13)
其中,Q表示自由度为k的t分布,其概率密度函数为f(t;k):
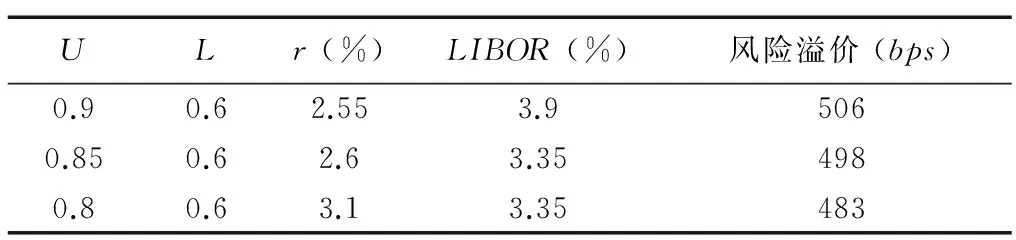
(-∞ (14) S*(y)=Q[Φ-1(S(y))+y] (15) 双因素转换模型不仅考虑了概率变换,也对参数进行了不确定性调整,其目的是用来测度巨灾债券和长寿债券的风险溢价。 (二)长寿债券其他相关假设 1.年限及运行。本债券设计年限为15年,具体设计思路见本文第二部分。 2.无风险利率。即无风险收益率,一般将一年期国债利率或者银行三个月定期存款利率作为无风险利率,投资者可以以这个利率进行无风险借贷。 3.LIBOR。银行间同业拆借利率是市场借贷利率的基础,所以,能较好地反映一项投资的基本收益。 (三)双因素Wang转换定价过程 本文在长寿债券定价实证中采用带永久跳跃的APC模型,其中时间因子kt如公式(9)所示。 由于双因素Wang转换比单因素Wang转换解释长寿市场价格更具有一致性,因此,使用双因素Wang转换分别对变量Z、Y和N进行转换,并假定Z、Y和N相互独立。令λ1、λ2和λ3分别代表与Z、Y、N三个变量相关的风险市场价,在风险调整测度Q下死亡率时间因子为: (16) Cox、Lin和Wang(2006)、Chen和Cox(2009)都基于永久跳跃的死亡率模型和λ1=λ2=λ3=λ的假设估计了瑞士再保险公司于2003年发行的巨灾债券的风险市场价,分别为0.83和0.8072。前者是基于死亡率qt的随机跳跃过程,后者是基于死亡率时间因子kt。本文将采用后者方法,针对时间因子kt的随机跳跃过程模型中的三个变量Z、Y、N分别进行转换,并假定长寿债券的风险溢价为λ1=λ2=λ3=λ。具体计算过程如下: (1)基于时间因子模型kt+1=kt+μ-pm+σZt+1+Yt+1Nt+1,模拟kt10 000次(t取2004—2018年),假定k0=-12,模型中其他参数估计值见表1。 (4)计算损失率。 设定下触碰点L=0.6S0和初始上触碰点U=0.9S0,其中,S0=q0代表2003年生存指数。固定下触碰点在0.6S0,改变上触碰点,分0.9S0、0.85S0和0.8S0三个档次。 (5)使用无风险利率,将长寿债券每期的息票和最终返还的本金贴现到2004年初,并通过以下方程计算该长寿债券的风险溢价: (17) 其中,P是长寿债券的签发规模 (比如100万元人民币),r代表无风险利率,L是12个月同业拆借利率(LIBOR),计算结果如表2所示。 表2 Wang转换下长寿债券的风险溢价 从表2可知,固定长寿债券的下触碰点为0.6S0,即若生存指数触及该点,就发生完全的长寿事件,投资者的本金将无法收回;同时将初始上触碰点设置为0.9S0、0.85S0、0.8S0三个情景,风险溢价结果分别为506个基点(即5.06%)、498个基点(即4.98%)和483个基点(即4.83%)。结果表明,随着初始上触碰点的下移,风险溢价逐渐降低。这与理论分析结论是一致的,因为初始上触碰点越低,发生首次触碰的概率就越小,投资人的本金损失率也越小,即投资风险下降,因此,长寿债券的风险溢价应该低一些。 另外,从表2也可以看到,在双因素Wang转换定价方法下,长寿债券的风险溢价对无风险利率和LIBOR的假设条件要求比较高。也就是说,无风险利率和LIBOR的微小变化都会对风险溢价的结果产生大的波动,甚至出现不合理的结果(如出现负值)。这可能是由于我国人口死亡率可用数据年限很短,而带永久跳跃的随机死亡率模型参数太多,引起模型参数不稳定,进而导致风险溢价结果的敏感性很高。 上述实证表明,双因素Wang转换对本文设计的债券和中国的人口死亡率数据敏感性较高,波动性较大。这可能是因为目前中国人口死亡率可用数据时间很短,只有20年,容易导致死亡率模型参数不够稳定,进而对定价结果产生影响。因为同样的方法用美国的人口数据定价就不会有这样的问题(见Chen和Cox, 2009),美国可用的人口数据有上百年。因此,精算师们今后对长寿债券设计和定价时,应多关注模型风险和参数风险。同时,基于模型风险的重要性,在定价实务中可以考虑通过一组模型来处理模型风险。例如,对于给定的数据,根据BIC标准给每个模型分配一个权重,然后综合计算债券的溢价。 在长寿风险日趋严峻的今天,再保险、自然对冲等传统的长寿风险转移方式所能发挥的作用受到很多局限,资本市场衍生工具这类新型的长寿风险转移方式将会发挥越来越大的作用,尤其是长寿债券,具有巨大的市场潜力。长寿债券对我国来说是个新生事物,未来其实现机制应着重从监管机制、法律机制和政府激励机制等方面展开。 首先,应认可并大力支持长寿债券业务的发展,并创新监管制度,确立与长寿债券运行相配套的政府监管边界,为长寿债券顺利运行提供条件。其次,应通过立法允许相关法人或保险人从事长寿风险债券业务。再次,政府应出台相关的法律法规,进一步完善资本市场,鼓励成熟投资者进行以套期保值和套利为目的的投资工具交易,增加资本市场长期债券的种类与份额,为死亡率指数相关金融衍生品的发行和交易创造良好的投资环境和交易平台。 注释: ① 我们倾向于离散时间的死亡率模型,主要是考虑到:(1)死亡率最多一年测算一次;(2)在定价过程中,离散时间死亡率模型相对容易被理解和执行;(3)死亡率在短期内不会有大的改善;(4)大部分年金和债券的息票都是以离散方式支付的。 [1] Blake D, Burrows W.Survivor bonds: helping to hedge mortality risk[J].Journal of Risk and Insurance, 2001, 68 (2): 339-348. [2] Wang S.A class of distortion operation for pricing financial and insurance risks[J].Journal of Risk and Insurance, 2000,67:15-36. [3] Wang S.A universal framework for pricing financial and insurance risk[J].ASTIN Bulletin,2002,32(2): 213-234. [4] Bauer D, M Börger,J Russ.On the pricing of longevity-linked securities[J].Insurance: Mathematics and Economics, 2010, 46:139-149. [5] Cairns A, Blake D, Dowd K.A two-factor model for stochastic mortality with parameter uncertainty: theory and calibration[J].Journal of Risk and Insurance, 2006b, 73: 687-718. [6] Bauer D, Ruβ J.Pricing longevity bonds using implied survival probabilities[R].Discussion Paper, University of Ulm.2006. [7] Lin Y,S H Cox.Securitization of mortality risks in life annuities[J].Journal of Risk and Insurance, 2005,72: 227-252. [8] Cummins J D, Lalonde D, Phillips R.The basis risk of catastrophic-loss index securities[J].Journal of Financial Economics, 2004,71 (1): 77-111. [9] Cummins J D, Weiss M.Convergence of insurance and financial markets: hybrid and securitized risk transfer solutions [J].Journal of Risk and Insurance 2009,76 (3): 493-545. [10] 谢世清.长寿风险证券化的理论研究动态[J].保险研究,2014(3):72-77. [11] 尚勤,秦学志.随机死亡率和利率下退休年金的长寿风险分析[J].系统工程,2009(11):56-61. [12] 尚勤,秦学志,张悦玫,胡友群.基于Copula函数和王变换的巨灾死亡率债券定价研究[J].大连理工大学学报,2012(1):139-145. [13] 胡仕强.基于Lee-Carter模型和王变换方法的长寿债券定价研究[J].商业研究,2015(10):82-88. [14] 尚勤,秦学志,周颖颖.巨灾死亡率债券定价模型研究[J].系统工程学报,2010(2):28-30. [15] Beelders O, Colarossi D.Modelling mortalityrisk with extremevalue theory: the case of Swiss Re'smortality-indexed bond[R].Global Association of Risk Professionals, 2004. [16] Biffis E, Blake D.Keeping some skin in the game: how to start a capital market in longevity risk transfers [J].North American Actuarial Journal, 2014, 18(1):14-21. [17] Lee R D,Carter L R.Modeling and forecasting US mortality[J].Journal of the American StatisticalAssociation, 1992, 87:659-675. [18] Renshaw A,Haberman S.Lee-Carter mortality forecasting with age-specific enhancement[J].Insurance: Mathematics and Economics,2003,33: 255-272. [19] Renshaw A,Haberman S.Cohort-Based extension to the Lee-Carter model for mortality reduction factors [J].Insurance: Mathematics and Economics, 2006, 38:556-570. [20] Cairns A, Blake D, Dowd K.Modeling and management of mortality risk: a review[J].Scandinavian Actuarial Journal, 2008,23:79-113. [21] CairnsA, Blake D,DowdK,Coughlan G.D,Epstein D,Ong A,BalevichI.A quantitative comparison of stochastic mortality models using data from England & Wales and the United States[J] North American Actuarial Journal, 2009,13: 1-35. [22] Dowd K,Cairns A,Blake D,Coughlan G.D,Epstein D,K halaf-Allah M.Evaluating the goodness of fit of stochastic mortality models [J].Insurance: Mathematics & Economics, 2010a, 47: 255-265. [23] Dowd K,Cairns A,Blake D,Coughlan G.D,Epstein D,K halaf-Allah M.Backtesting stochastic mortality models: an ex-post evaluation of multi-period-ahead density forecasts [J].North American Actuarial Journal, 2010b, 14:281-298. [24] LiS H, W.S Chan, The Lee-Carter model for forecasting mortality, revisited [J].North American Actuarial Journal, 2007,11(1): 68-69. [25] Cox S H, Lin Y,Wang S.Multivariate exponential tilting and pricing implications for mortality securitization[J].Journal of Risk and Insurance, 2006, 73(4): 719-736. [26] Chen H,Cox S H.Modeling mortality with jumps: applications to mortality securitization [J].Journal of Risk and Insurance, 2009, 76: 727-751. [27] Wang S.A class of distortion operation for pricing financial and insurance risks [J].Journal of Risk and Insurance, 2000,(67): 15-36. [28] Wang S.Cat bond pricing using probability transforms[J].In special issueson insurance and the state of the art in cat bond pricing,2004, 278:19-29. (责任编辑:宁晓青) Pricing Longevity Bonds Using Two-factor Wang Transform Approach FAN Yi1,2,ZHANG Ning3,WANG Yaozhong1 (1.CollegeofEconomicsandTrade,HunanUniversity,Changsha,Hunan410079,China; 2.CollegeofEconomics,CentralSouthUniversityofForestryandTechnology,Changsha,Hunan410004,China; 3.CollegeofFinanceandStatistics,HunanUniversity,Changsha,Hunan410079,China) Based on the assumption of discrete mortality model and comparison of foreign classic bond, we design a longevity bond with adjustment-upper trigger point and price the longevity bond by using the APC model with permanent jumping and double-factor Wang transform.The empirical results show that risk premiums are all in a reasonable range under different combination of parameters.The result of risk premium is sensitive to the parameters such as risk-free interest rate because of using the multi-parameters model and lack of the available mortality data. longevity risk bond;two-factor wang transform;mortality;pricing 2017-01-14; 2017-03-08 湖南省社会科学基金项目(11YBA343、14YBA093)、湖南省情与决策咨询项目(2012BZZ29)、湖南省教育厅优秀青年项目(17B286)、中南林业科技大学青年基金重点项目(2012ZD05)、国家社会科学基金项目(17BJL048). 樊毅(1983—),女,湖南常德人,湖南大学经贸与贸易学院博士研究生,中南林业科技大学经济学院讲师,研究方向:风险管理与保险。 F840.65 A 1003-7217(2017)04-0032-07

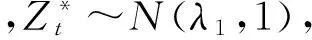
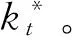
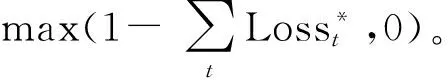
五、结论与建议
——买房还息的小技巧

