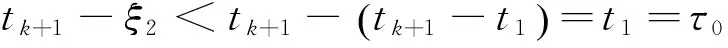基于不均匀网格的分数阶微分方程差分格式及系数性质

刘彦芝

(吕梁学院 数学系，山西 离石 033001)

·数学研究·

基于不均匀网格的分数阶微分方程差分格式及系数性质

刘彦芝

(吕梁学院 数学系，山西 离石 033001)

非均匀网格；梯形公式；隐差分格式

分数阶微分方程产生于一些反常扩散模型，具有深刻的物理背景和丰富的理论内涵，可广泛应用于科学和工程的各个领域.当前，对分数阶微分方程的研究已引起众多学者的广泛关注[1-4].与经典的整数阶微分方程相比，分数阶微分方程具有非局部性、遗传性等特征，因而对其进行深入理论研究并建立行之有效的差分格式仍较为困难.

本文考虑如下非线性分数阶初值问题:

(1)

为保证方程(1)解的存在唯一性，我们假定f关于第二个变量满足Lipschitz条件，即

1 差分近似

将方程(1)化为Volterra积分方程[1]：

(2)

(3)

其中

2 主要结论

引理1[5]如果α>0,k为非负整数，τi≤τi+1,j=0,1,…,k,则由(4)式定义的系数ωj,k+1有如下估计成立：

证明：j=0 时，利用中值定理，得

其中tk+1-t1<ξ1<ξ2

所以

若α≥1,则

若0<α<1,

当j=1,2,…,k时，由(4)得

其中，tk+1-tj+1<ξ3<ξ4

(5)

其中，tk+1-tj<ξ6<ξ5

(6)

若α≥1，由(5)(6)得

若0<α<1，由(5)得

同理可得

所以有

当j=k+1时，

综上得证.

由于解非线性问题需要用到Gronwall不等式，文献[5]中对Gronwall不等式进行了改进，要求系数满足特定条件，而这正是引理1所证明的结论，为后续证明差分格式的稳定性及收敛性提供了前提.

[1]K.Diethelm,N.J.Ford.Analysis of fractional differential equationns[J]．Math.Anal.Appl，2002(2).

[2]K.Diethelm,N.J.Ford.Detailed error analysis for a fractional Adams method[J]．Numerical Algorithms，2004(36).

[3]C.P.Li,F.H.Zeng.Finite difference methods for fractional ddifferential equations[J]．Comput.Math.Appl，2009(58).

[4]刘发旺，庄平辉，刘青霞.分数阶偏微分方程数值方法及其应用[M].北京：科学出版社，2015.

[5]C.P.Li,Q.Yi,A.Chen，Finite difference methods with non-uniform meshes for nonlinear fractional differential equations[J]．Journal of Computational physics，2016(316).

[6]M.Stynes,E.Riordan,J.L.Gracia，Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation[R]．北京：北京计算科学研究中心，2016.

2017-02-08

吕梁学院青年基金项目(ZRQN201521).

刘彦芝(1985-)，女，山西柳林人，助教，研究方向为计算数学.

O151

A

2095-185X(2017)02-0001-03