悬臂梁式动力吸振器多频减振研究

周荣亚

（陕西铁路工程职业技术学院，陕西 渭南 714000）

悬臂梁式动力吸振器多频减振研究

周荣亚

（陕西铁路工程职业技术学院，陕西 渭南 714000）

将悬臂梁作为动力吸振器附加在振动主结构上来达到振动抑制的目的，数值计算分析表明悬臂梁式动力吸振器具有多频减振特性。按照模态理论建立基于悬臂梁的具有集中参数的等效复式动力吸振器模型，悬臂梁的每一阶模态作为一个自由度的弹簧质量系统，把悬臂梁每阶模态的有效模态质量和等效模态刚度作为每一自由度弹簧质量系统的集中质量和刚度。用悬臂梁式动力吸振器的附加动刚度验证等效复式动力吸振器模型的正确性。将悬臂梁式动力吸振器附加在主梁末端，调谐悬臂梁式动力吸振器的前4阶模态达到对主悬臂梁的多频减振效果，证实了悬臂梁式动力吸振器多频减振特性。

振动与波；悬臂梁；复式动力吸振器；有效模态质量；多频减振

振动是人们在生产生活中不可避免的现象，振动的存在使得工业生产设备产生疲劳破损，影响设备的精度，甚至缩短设备寿命。同时由于振动的存在又会形成噪声问题，降低人们生活质量。于是减振降噪成为科学研究的一大领域，形成了隔振、阻尼减振、动力吸振等多个技术研究方向。

动力吸振器由Frahm在1909年首先发明[1]，直到现在的百年发展时间内有了大量的研究成果。动力吸振器的研究大致经历了从单自由度到多自由度、从离散到连续、从单一参数调谐到多参数联动调谐的发展过程[2]。目前，单自由度和多自由度动力吸振器应用于连续体来进行宽频减振仍然是研究的热点。El-Khatib等人将单自由度动力吸振器附加在梁上来抑制梁中弯曲波的传播[3]。

D.J.Thompson研究了用基体梁上连续分布的单自由度动力吸振器抑制梁中宽频弯曲波传输的特性[4]。Cheng Yang等将多个单自由度动力吸振器附加于平面矩形薄板，研究动力吸振器宽频带减振特性[5]。

动力吸振器已有很多实际工程应用案例，例如轨道交通领域，许多动力吸振器产品被开发应用于轨道以及车轮等，达到了非常好的减振降噪效果。悬臂梁式动力吸振器由于结构简单、工程适用性强，成为研究的热点[6]。王彦琴等用功率流的方法研究变截面悬臂梁式动力吸振器作用在矩形薄板上的宽带减振机理，从减振效果上证实了悬臂梁式动力吸振器由于模态丰富，在每阶模态处均有动力吸振器的效果，但是用功率流的方法并没有把悬臂梁式动力吸振器的复式动力吸振器动力学参数识别出来[7]。

到目前为止，悬臂梁被设计成动力吸振器时仍然被视作具有单自由度特性。悬臂梁本身提供等效弹性元件和等效质量元件，或者将悬臂梁末端附加质量块，仅将悬臂梁等效为弹性元件。张针粒等提出悬臂梁式动力吸振器的分布质量模型，以悬臂梁式动力吸振器的固有频率为评判指标讨论了分布质量模型的优越性[8]。

文中将悬臂梁式动力吸振器等效为具有多频吸振特性的复式动力吸振器，引入悬臂梁多阶模态，根据模态理论识别出悬臂梁各阶模态的等效动力学集中参数，以悬臂梁根部的附加动刚度为评判指标验证等效模型的正确性。最后将悬臂梁式动力吸振器附加到主结构上，用有限元法求解振动响应，证实了悬臂梁式动力吸振器的多频减振特性。

1 等效复式动力吸振器模型

图1为悬臂梁式动力吸振器连接的示意图及等效弹簧质量振子模型。

图1 悬臂梁式动力吸振器示意图

如图1(a)所示，悬臂梁式动力吸振器与主结构连接时通常成对使用，从而避免了悬臂梁对主结构的弯矩作用。悬臂梁的长设为l，截面为矩形，其宽和高分别设为br、hr，悬臂部分的长度为lr。悬臂梁根部与主结构固连部分的长度为ls=2(l-lr)。

目前，悬臂梁的等效振子系统通常是单自由度的，如图1(b)所示；其中等效振子质量mr是悬臂段质量的0.605倍，悬臂段lr的其余部分质量与固连部分质量ms共同构成了m0。实际上，图1(b)所示的等效单自由度弹簧质量振子系统也是悬臂梁式动力吸振器的一个近似等效模型，该等效模型只是应用了悬臂梁的第1阶模态，然而在实际振动过程中包含了悬臂梁的多阶模态，因此需要将悬臂梁等效为复式的弹簧质量振子系统才能更准确描述悬臂梁式动力吸振器的振动行为。

考虑悬臂梁的多阶模态，将图1(a)所示的悬臂梁振子等效为如图1(c)所示的等效复式动力吸振器系统，该等效过程就是要找到悬臂梁第i阶模态的等效质量mri和等效刚度kri。地震力学的研究中常将建筑物等效为悬臂梁，在用模态叠加法计算建筑物受到大地激励的振动响应时用到有效模态质量，其具有质量的量纲，用有效模态质量所占总质量的百分数来判断计算所用的模态阶数通常会得到准确的结果。

在研究中，将悬臂梁式动力吸振器每一阶模态的有效模态质量作为该阶模态的等效质量也会取得精确的等效模型。下面来说明有效模态质量。按照有限元的方法将悬臂梁离散为多自由度振动系统。在外激励作用下，多自由度振动系统的振动方程可以表示为

式中M、C、K分别表示系统的质量阵、阻尼阵和刚度阵，X、F分别是位移列阵和力列阵。

令φ为特征向量矩阵，则为第i阶模态的广义质量。

当悬臂梁根部受力方向是沿着悬臂梁横向方向y轴时，第i阶模态的模态振型参与因子γi为

第i阶模态的有效模态质量为

有效模态质量有质量的量纲，并且各阶有效模态质量的总和为系统的总质量。在单一的方向上也满足这个关系，即

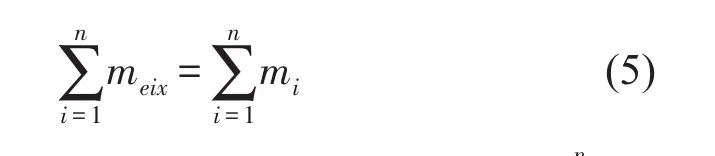
式中n表示系统为n自由度，x表示在x方向表示系统总质量。

对于一根连续欧拉梁，有效模态质量的定义为

式中n表示第n阶模态，ρ(x)表示梁单位长度的质量即梁的线密度，Yn(x)是质量正则化的特征向量。

对于悬臂梁振子，其等效复式振子的第i阶等效质量mri=me,i，容易求得悬臂梁振子的固有频率为ωri，则有kri=mriωri2。只考虑悬臂梁前四阶模态，其等效复式动力吸振器的每1阶等效质量如表1所示。

表1 等效质量

2 等效模型验证

悬臂梁式动力吸振器对主结构的动态力效应用由悬臂梁通过根部连接位置输入到主结构中的动刚度Dr来描述。在这一部分通过对比悬臂梁及其等效复式动力吸振器输入到主结构中的动刚度来评价等效复式模型的正确性，如果等效模型是正确的，其动刚度应该和悬臂梁的动刚度是一致的。

悬臂梁式动力吸振器与主结构固连部分的动刚度是

式中ms=ρrArls,其中,ρr为悬臂梁的密度,Ar为悬臂梁振子的横截面面积。需要说明的是，在实际工程应用中通常将一根梁中间部分用螺栓等连接件与主结构连接,当连接件的质量较大不能忽略时，ms应当包含螺栓等连接件的质量。文中涉及的理论分析模型和样件的连接件质量很小，所以为了简便，连接件的质量忽略不计。

悬臂梁lr段输入到主结构中的动刚度是

图1(c)所示的等效复式动力吸振器模型中，固连到主结构中的质量m0=ms，该部分的附加动刚度为

等效复式动力吸振器第i阶弹簧质量振子系统的附加动刚度

并联的弹簧质量振子系统的总动刚度为各个单自由度弹簧质量振子系统的加总和。如果将悬臂梁的前n阶模态等效为复式弹簧质量振子系统，则等效复式动力吸振器系统的附加动刚度为

设定悬臂梁式动力吸振器的材料和尺寸参数如表2所示，将悬臂梁式动力吸振器及其等效复式动力吸振器的附加动刚度进行对比，如图2所示。

表2 悬臂梁式动力吸振器参数

在0～800 Hz频率范围内，悬臂梁式动力吸振器共有3阶振动模态，其对应的附加动刚度在每1阶模态频率处出现一个峰值。等效复式动力吸振器的附加动刚度与悬臂梁式动力吸振器的附加动刚度有相同的峰值频率，但是等效复式动力吸振器的附加动刚度的量值有偏差，这是因为模态截断使得只有有限阶模态被引入等效复式动力吸振器附加动刚度的计算当中。当等效复式动力吸振器包含的模态数增加时，其附加动刚度的值也越接近于准确值。也就是图2中De,n的n增加时，De,n的值越接近于准确值Dr。

图2 悬臂梁式动力吸振器附加动刚度

3 悬臂梁式动力吸振器多频减振分析

利用悬臂梁的多阶模态来形成复式动力吸振器可以达到多频减振效果。但是要将悬臂梁的多阶模态频率调谐到多个目标减振频率上并不容易，因为对于恒定截面的悬臂梁，其每阶固有频率都有一定的倍率关系。这也是大家往往只针对悬臂梁的第1阶模态进行等效形成单自由度动力吸振器的原因。只应用悬臂梁的第1阶模态固然便于调整参数进行设计，但是这不可避免地忽视了悬臂梁式动力吸振器高阶模态对减振效果的影响，同时不利于在悬臂梁式动力吸振器中增加更多的阻尼效果，因为在悬臂梁表面粘贴阻尼是增加悬臂梁式动力吸振器阻尼的一般方法，但是敷设阻尼材料后，悬臂梁的高阶模态产生更多的模态变形，从而在高阶模态处悬臂梁式动力吸振器能获得更大的阻尼。

将悬臂梁式动力吸振器附加在一根主悬臂梁上，调整悬臂梁式动力吸振器的参数使其达到对主梁的多阶模态振动抑制效果，验证悬臂梁式动力吸振器的多频减振特性。主悬臂梁的密度和弹性模量分别为ρ=7 850 kg/m3，E=200 Gpa，其尺寸设定为1 200 mm×36 mm×36 mm；悬臂梁式动力吸振器的尺寸设定为200 mm×36 mm×1 mm，材料参数设置与主悬臂梁相同。将悬臂梁式动力吸振器附加在主悬臂梁的末端，无固连长度，如图3所示。

图3 振动响应求解设置

利用Ansys有限元软件计算其振动响应。计算时在主梁距离固定端300 mm处沿着主梁的横向方向施加0～800 Hz、幅值为1 N的简谐激励。在主梁的一侧均布6个振动响应拾取点，间隔为200 mm。求解0～800 Hz范围内振动响应，将6个响应点的振动加速度值的算术平均值与未加动力吸振器时对应的振动响应对比，分析悬臂梁式动力吸振器的减振效果，如图4所示。

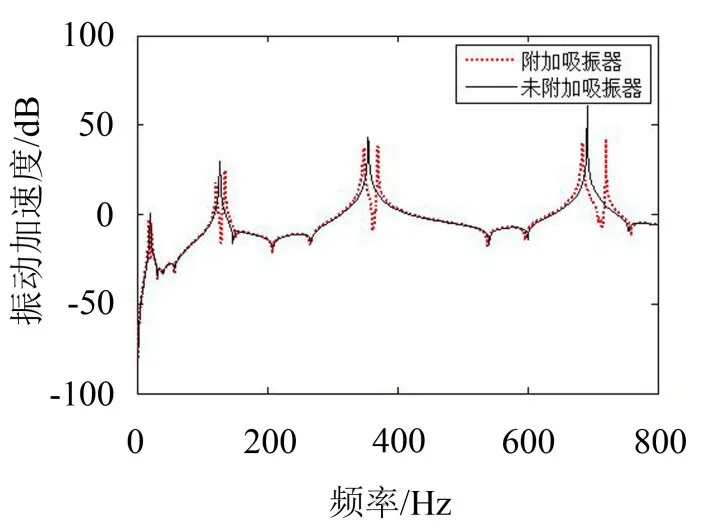
图4 悬臂梁式动力吸振器多频减振效果

在0～800 Hz范围内，未附加悬臂梁式动力吸振器的主梁的振动响应出现了4个峰值，4个峰值处的频率即是各阶模态频率。对附加的悬臂梁式动力吸振器的尺寸进行特定的设定，可以将其各阶频率调谐到与主悬臂梁各阶模态频率一致，这样悬臂梁式动力吸振器实际上是以复式动力吸振器的形式对主梁起到吸振的作用。图4中可以明显看到，附加悬臂梁式动力吸振器后，在主梁的各阶模态上均有动力吸振效果。前3阶模态上，悬臂梁式动力吸振器的吸振效果达到5 dB，在第4阶模态上，吸振效果高达28 dB。

4 结语

建立悬臂梁式动力吸振器的等效复式动力吸振器模型，根据模态叠加理论，精确确定复式动力吸振器模型中各个单自由度吸振器的集中质量和等效刚度。以悬臂梁通过根部输入到主结构中的附加动刚度为评判指标验证了等效复式动力吸振器模型的正确性。将悬臂梁式动力吸振器应用于主梁结构，通过参数调整达到多频减振效果，证实悬臂梁式动力吸振器的多频减振特性。在实际悬臂梁式动力吸振器减振参数设计中，文中的复式动力吸振器模型能够提供精确的参数量值，进行精确的调谐。

[1]FRAHM H.Device for damping vibrations of bodies:U.S.patent,989958[P].1909,3576-3580．

[2]刘耀宗，郁殿龙，赵宏刚，等.被动式动力吸振技术研究进展[J].机械工程学报，2007，43(3)：14-18.

[3]EL-KHATIB H M,MACE B R,BRENNAN M J.Suppression of bending waves in a beam using a tuned vibration absorber[J].Journal of Sound and Vibration,2005,288:1157-1175.

[4]THOMPSON D J.A continuous damped vibration absorber to reduce broad-band wave propagation in beams[J].Journal of Sound and Vibration,2008,311:824-842.

[5]CHENG YANG,DEYU LI,LI CHENG.Dynamic vibration absorbers for vibration controlwithin a frequency band[J].Journal of Sound and Vibration,2011,330(8):1582-1598.

[6]CAVACECEA M,VITAB L.Optimal cantilever dynamic vibration absorbers by Timoshenko beam theory[J].Shock and Vibration,2002,11(3):199-207.

[7]王彦琴，盛美萍，孙进才.变截面梁式动力吸振器的宽带吸振机理[J].振动工程学报，2004，17(4)：473-476.

[8]张针粒，李强，刘记心，等.悬臂式动力吸振器的分布质量模型[J].噪声与振动控制，2014，34(5)：38-41.

Vibration Reduction Effect of Cantilever Type Vibration Absorbers in Multi-frequency Band

ZHOU Rong-ya
（Shanxi Vocational Technical Institute of Railway Engineering,Weinan 714000,Shanxi China）

Cantilever type dynamic vibration absorbers can be attached to the principal structure to suppress vibration effectively.Numerical analysis shows that the cantilever type absorbers have multi-band vibration reduction characteristics.In this paper,the equivalent multiple spring-mass oscillator system model of the cantilever type dynamic vibration absorber is established according to the modal superposition theory.Each mode of the cantilever type dynamic vibration absorber is treated as a single DOF spring-mass oscillator system.The effective modal mass and effective modal stiffness of each mode are treated as the lumped mass and stiffness of the equivalent multiple spring-mass oscillator system.The correctness of the multiple spring-mass oscillator system model is verified by dynamic stiffness test of the cantilever type absorber.Finally,the cantilever type dynamic vibration absorber is attached to the end of the principal beam,and the first 4 modes of the absorber are found to reach the effect of multi-band vibration reduction.

vibration and wave;cantilever beam;multi-DOF vibration absorber;effective modal mass;multi frequency vibration reduction

TB535.1

：A

：10.3969/j.issn.1006-1355.2017.04.039

1006-1355(2017)04-0197-04

2017-02-01

周荣亚（1988－），男，山东省临清市人，工学硕士，主要研究方向为振动噪声控制。

E-mail:zryrongya@163.com