绳系拖曳离轨模型及脉冲喷气控制策略的可行性
刘新建,郑杰匀
(国防科学技术大学航天科学与工程学院,长沙 410073)
绳系拖曳离轨模型及脉冲喷气控制策略的可行性
刘新建,郑杰匀
(国防科学技术大学航天科学与工程学院,长沙 410073)
在空间绳网的绳系组合体拖曳变轨运动控制中,系绳张力控制策略需要有一套卷扬机构及张力检测控制装置,将增加机构的质量、复杂度和成本,并降低操作可靠性。提出仅利用拖船飞行器上的三轴正交喷嘴控制策略,可同时实现拖曳离轨中的相对运动控制和系统质心的轨道控制,而系绳张力只作为约束,推导了组合体拖曳离轨的三维空间运动动力学模型,给出了一种准霍曼拖曳离轨控制方法,完成了同步轨道废弃目标拖曳离轨方案的初步可行性仿真验证,并给出了拖曳过程的喷气力、燃料消耗量指标,可供空间绳网研究参考。
空间绳网;绳系组合体;拖曳离轨动力学;脉冲喷气控制
0 引言
过去,国内外对绳系卫星的动力学与控制研究较多[1-12], 但近年来,空间绳网成为空间碎片清理领域的一个热门研究方向,如欧空局的Roger项目[14]。绳网展开捕获锁紧目标后,任务星(拖船)、目标与系绳成为了组合体。绳系组合体与绳系卫星系统的不同之处在于:1)绳系组合体的目标通常是大型空间碎片或者废弃失效卫星,而绳系卫星为合作目标;2)绳系组合体的系绳长度较短,为几十米至上百米,而绳系卫星的系绳长达几十千米;3)绳网碰撞收口空间目标之后,初始状态发生瞬间变化,尤其是绳网锁紧目标连成一体后对任务星的相对角速度是任务星拖曳变轨任务主要的初始干扰源,绳系卫星系统的任务主要是释放和回收卫星;4)绳系组合体要求有主动变轨,控制至给定的轨道高度离轨,而变轨力严重影响组合体之间的相对运动,可能导致不允许的碰撞和缠绕现象发生,所以绳系组合体拖曳变轨问题是绳网应用的另一重要研究方向。
绳系组合体的动力学研究主要考虑2维轨道面内的运动,如Liu等[14]建立了绳系组合体轨道面内运动的2维动力学模型,但3维空间运动动力学模型的研究不足;绳系组合体的控制研究也借鉴绳系卫星,主要开展了轨道面内系绳张力的稳定控制问题,但系绳张力控制策略需要有一套卷扬机构及张力检测控制装置,增加了空间绳网机构的质量、复杂度和成本,并降低了操作可靠性。国内外对绳网组合体拖曳离轨控制的其他研究文献不多,而且对拖曳离轨的能量需求没有给出具体的参考结果。
如果单纯利用拖船飞行器上的三轴正交喷嘴同时实现拖曳离轨中的相对运动控制和系统质心的轨道控制,则非常有意义。本文先建立绳系组合体拖曳离轨运动的空间运动动力学模型,然后给出一种脉冲控制策略及方法,最后以同步轨道碎片清理的拖曳离轨为背景完成仿真算例,探讨能量需求和可行性。
1 绳系组合体拖曳离轨运动的空间运动动力学模型
1.1 系统描述
为研究控制策略,首先需要研究组合体轨道运动与相对质心转动的系统动力学。考虑由目标S1、拖船S2及连接两者的系绳组成的空间绳系离轨系统,如图1所示。作如下基本假设:地球视为均质球体,完全中心引力场;目标和拖船视为集中质点,忽略系绳的质量;系绳不能抗压也不能抗弯,系绳有纵向的弹性和阻尼;只考虑系统面内的轨道转移,由安装在拖船上的推力器实现。
假设系统质心运动的升交点赤经Ω、轨道倾角i变化忽略不计,沿体坐标系x1轴的推力大小为F,相对轨道坐标系的姿态角3-2-1 Euler角俯仰、偏航和滚动角α、β、γ表示。系统的轨道运动用地心距r、极角u和垂直轨道面的横向位移z来描述;描述系统相对运动的参数有:目标和拖船的距离d、系绳的面内摆角θ、面外摆角φ。
引入以下3个坐标系:
1)地心惯性系O-XYZ,原点为地心O,三轴方向上的单位矢量分别为I、J、K,其中X轴指向春分点r,Z轴垂直于赤道面指向北极,Y轴由右手法则确定。
2)轨道坐标系S0-xyz,原点为系统质心S0,三轴方向上的单位矢量分别为i、j、k,其中x轴由O指向S0,y轴在轨道面内垂直于x轴并指向运动方向,z轴由右手法则确定。
目前工伤保险医疗费是鉴定后单位提供病历发票,社保机构手工录入人工审核后发放。发生工伤就近(非定点)治疗、伤情需市外转诊、工伤职工异地居住需要就医、旧伤复发治疗等情况还需单位填表申请,审核后才可以就医。现行的医疗费审核和结算方式周期长,延误了就医时间,增加了单位和个人垫付费用的负担,审核落后与先进的医疗水平脱轨,不利于医生救治。部分老工伤人员长期以伤养病,造成医疗资源浪费工伤基金流失。

1.2 动力学方程组
设S1、S2的质量分别为m1、m2,则系统总质量为m=m1+m2。设S1、S2到S0的距离分别为d1、d2,则
(1)

由表6可知:应用聚丙烯纤维微表处养护维修技术,相比于普通纤维微表处多了1.1元/m²的原料成本,普通微表处技术每平方成本约为15元/m²,聚酯纤维微表处相比于普通微表处增加成本7%,但极大地提高了路面的使用寿命,具有较高的经济效益。
(2)

通过开展教育培训、文化下乡等实践活动,构建终身教育体系,地方高校可以通过农村基础教育、多种形式的教育培训、文化下乡等实践活动来帮助农民扩展知识,开阔视野,提高文化生活质量,进而更新农民观念,促进传统农民向新型农民的转变,改进村风村貌,促进农村民主化发展,弘扬当地先进文化,加强精神文明建设,最终全面提升农村文化建设水平。
(3)
对于平面内的轨道运动,有
(4)
由刚体动力学知,体轴系的旋转角速度为
(5)
(6)
综上可得动能表达式为
(7)

(8)
以同步轨道空间碎片清理为例,研究将其包裹收口后拖曳到高于同步轨道300km高度的坟墓轨道,然后切断系留绳离轨的准霍曼变轨控制策略。
(9)
1)防碰撞:整个离轨过程目标和拖船不得小于某个安全距离限,如图2中的L0。
应当注意此为理想情况,实际上由于飞行器处于一个未知的开放环境当中,往往会存在某方向的自然风,在这个自然风的影响下,飞行器会处于一个不平衡状态,可能会引起定向漂移或者失控,因此需要通过改变相应电机转速来引入一个反向分量去平衡这个自然风所引起的偏移量[18]。
(10)
定义广义坐标为q=(r,u,z,d,θ,φ)T,设Qr、Qu、Qz,Qd、Qθ、Qφ分别是与坐标r、u、z、d、θ和φ相对应的广义力,由虚功法计算广义力,推导过程详见参考文献[18],得
(11)
如果用体轴上的三轴喷嘴脉冲开关力来实现组合体的拖曳离轨控制,则对应轨道坐标系中的轨控开关力分量为Fx、Fy、Fz,上述方程中广义力的相关项只需用
Fcosαcosβ=Fx
Fsinαcosβ=Fy
-Fsinβ=Fz
替换即可,显然开关力有正、负、零3档。
综上所述,对于人格障碍患者而言,综合性护理干预具有有效性,可改善患者临床症状,纠正其不良行为,促使其早日融入社会。
取Lagrange函数为L=K-Ug,应用第2类Lagrange方程,然后舍去d/r2阶以上小量项,整理得到绳系组合体系统的空间运动方程组
(12)
式中,前3个方程描述的是系统质心的轨道运动,后3个方程描述的是系统相对运动,显然为非线性方程组。
2 绳系拖曳离轨的控制策略
2.1 拖曳变轨的安全约束
2.观察组和对照组患者手术并发症发生情况比较:观察组CP患者术后感染2例,无肠胀气、疼痛、出血及穿孔等并发症发生,其手术并发症发生率为1.4%;对照组CP患者术后出现并发症16例,其中肠胀气3例、疼痛5例、出血3例、穿孔2例、感染3例,并发症发生率11.6%。观察组CP患者手术并发症明显低于对照组,差异有统计学意义(P<0.05)。
针对拖曳离轨过程防碰撞、防断裂、防缠绕要求,需要设定基本的安全约束。
评选全国食药监管系统先进集体和先进工作者,是一件盛事,经过严格的推荐单位自审、省级初审、全国复审,经本单位、省级范围公示,候选名单“汇总速递”到北京。2016年12月21日~27日经国家总局网站在全国范围内公示,最终评出了45个全国食品药品监督管理系统先进集体、23个先进工作者。本刊在新年伊始,向广大读者隆重推出!榜样的力量是无穷的。先进集体和先进个人的闪亮登场,将成为新时代食药监人的楷模、全系统的标杆,也成为激励我们砥砺前行的动力。为了人民群众的食药安全,让我们向“双先”看齐,在新的一年努力工作,奋力疾奔。

组合体拖曳变轨过程中,通过安装在拖船飞行器上的相对测量设备(如雷达)保持对目标的连续跟踪观测,以获取目标的相对飞行状态。
总而言之,农村拥有广阔的天地,拥有丰富的教育资源。在农村幼儿园教育教学中,教师应当充分利用大自然中的各种资源,充分利用农村丰富的乡土资源,为幼儿营造一个良好的区域活动开展环境,保证幼儿的个性发展,促进农村幼教事业的不断进步。
2)防绷断:要求系绳张力不超过可承受的最大拉力。
3)防缠绕:当系绳处于松弛状态时,由于目标自身无动力,不能进行轨道控制,可能出现系绳与目标发生缠绕的现象,为此拖船要根据目标的相对飞行状态,进行相对转动控制,防系绳缠绕。
2.2 拖曳变轨策略及方法
虽然类似的看法并没有从这位牧马人车主的言谈举止中流露出来,但我也能体会到他从一开始接触到这辆全新梅赛德斯-AMG G 63 先型特别版时的些许抵触已经逐渐被主驾驶席上舒适、柔软且带有丰富按摩功能的designo Nappa真皮材质座椅所征服。如此说来,牧马人和G级越野车之间虽然拥有不少相似的进化历程,但至少在乘坐舒适性方面,全新G级越野车座椅的文明程度明显更高,当然选购的代价也更大。
变轨过程如图3所示:绳系组合体在地球静止轨道C1的A点产生速度冲量Δv1,转移到椭圆轨道E,它的近地点是A点,经过半个椭圆轨道周期,在椭圆的远地点B点产生速度冲量Δv2,使组合体满足进入坟墓轨道C2的状态要求。
根据轨道动力学理论得到总的所需特征速度增量为
(13)
其中,μ为地球引力常数,r1、r2分别为静止轨道C1、坟墓轨道C2的半径。
假设r1=42164km,r2=(42164+300)km,计算得所需霍曼脉冲变轨的特征速度增量仅为ΔvΣ=10.9m/s,但绳系组合体同步轨道准霍曼拖曳至300km坟墓轨道远没有霍曼变轨双脉冲简单,因为拖曳防碰撞和防缠绕产生的喷气力会使最终的轨道为小偏心率椭圆轨道,大致过程如下:
然而,大量调研发现,异步电动机负荷其实对10 kV配电网线路重合闸成功率影响不大。主要原因为目前工业电动机大多采用接触器进行投切,对于常见型号的接触器来说,当其电压跌落至45%~55%UN时,接触器将出现低压脱扣释放,延长释放时间为15~40 ms。由此可见,当重合闸时间整定在秒级时,负荷电动机早已经脱扣,无法提供短路电流和冲击电流,不会影响重合闸成功率。
第Ⅰ阶段:前期加速段,当绳网抓捕处于同步轨道的废弃目标后(假设处于近地点),拖船需要运动至同步轨道的V-bar方向,即将面内摆角控制在与地心矢径垂直的90°附近。如图3所示,面外摆角在0附近,然后对初始面内摆动角速度进行限制,期间喷气力也需控制相对运动,防碰撞、防缠绕,稳定后再施加切向脉冲推力,以提升组合体质心轨道的远地点高度,满足要求后停止加速。
第Ⅱ阶段:准霍曼自由转移阶段,完成约12小时轨道转移,期间喷气力只进行相对运动控制,避免碰撞和缠绕。
第Ⅲ阶段:离轨阶段,拖船运动至远地点,再次施加切向力,提升近地点高度,当满足要求后关闭喷嘴,并切断系绳使废弃目标进入坟墓轨道,完成离轨。期间除进行轨道控制之外,也需要进行相对运动的防碰撞、防缠绕控制。第Ⅲ阶段与第Ⅰ阶段的控制过程是相似的。
南北朝时期王微所著《叙画》、梁元帝所著《山水松石格》对“远”也有着各自的描绘。“远”在《叙画》中被描述成了“目有所极,故所见不周。于是乎以一管之笔,拟太虚之体……”[11]294。《山水松石格》记载:“造化为灵。设奇巧之体势,写山水之纵横。”[12]261到唐代王维提出“远人无目,远树无枝,远山无石”[13]32的“远人”、“远树”、“远山”的“三远”说;到五代荆浩又扩充到六“远”,“远山无皴,远水无痕,远林无叶,远树无枝,远人无目,远阁无基”[13]53。
2.2.1 变结构解耦控制律

d1=η2d,d2=η1d
现代化灌区作为一项重要的惠民工程,对工程总承包单位的综合实力具有一定的要求。通过投标等形式,筛选综合能力比较强的工程总承包单位完成灌区的建设,对保障工程建设质量是至关重要的。
(14)
则含非线性解耦的相对运动变结构控制律为
(15)
其中,ε、λ、k均为3×3正定对角阵,A1、A2是与相对运动方程中对应的非线性补偿解耦项。
患者均展开腹彩超多普勒超声的检查,同时进行诊断结果、手术病理证实的比较,选择GE型LOGIQP5与多普勒超声诊断仪进行,对探头频率进行选择时,需要按照2~9MHz标准进行[2]。患者以平卧位、侧卧位状态,保证膀胱充盈。选择彩色多普勒超声探头置于患者腹壁,在对患者胎儿和羊水进行了解后,对胎盘边缘、子宫颈间关系进行了解。在对探头方向进行相应调整后,引导患者正确进行体位变化,仔细观察胎盘边缘和子宫颈内关系,以便于进行有效诊断与分类。最后进行胎盘间隙与胎盘实质、周边血流的观察,同时掌握胎盘植入情况[3]。
为节省燃料,假设开关极限环阈值参数设置稍大点,为δd=5,δθ=2°,δφ=2°
2.2.2 增设缓冲环节
仿真发现,由于凯芙拉系绳虽然只有很小的直径(如2mm),但材料的弹性模量为120Gpa,为增强拖曳开关控制稳定性,需要在拖船任务星与系留绳的连接处串接一缓冲软弹簧,以降低系绳张紧的连接刚度,即拖船脉冲喷气力由缓冲弹簧再传递到系绳拉动目标。
3 数值仿真验证与分析
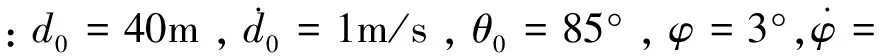
具体控制流程:绳网收口后100s内抑制初始干扰引起的相对运动,即相对接近速度为0,相对距离为30m;面内角度为90°,相对角速度为0。100s~190s,沿切向加速,完成系统霍曼转移的第一个速度增量,以提升远地点高度大于300km。190s~400s,为变结构开关控制,再次抑制切向加速对相对运动的干扰,之后进入准霍曼椭圆自由转移阶段,12h之后的某个时刻进行切向加速,提升近地点高度,当距离同步轨道300km后,切断系绳。仿真结果如下。
第Ⅰ阶段如图5所示,图6和图7中的各小图给出了全程3阶段约12h仿真结果。
图6中表明,实现了近地点离同步轨道300km,远地点离同步轨道419km的拖曳离轨控制,总的燃料只要22kg左右,面内摆角、面外摆角、相对距离均在期望值附近来回稳定小幅振荡,系绳张力小于150N。图7为三轴喷气力和燃料消耗曲线。
总的燃料消耗为22kg,具体组成为:第Ⅰ阶段消除初始相对状态误差的轴向防碰撞燃料为7.5kg,防缠绕面内摆角控制燃料为1.2kg,面外摆角控制燃料为1.2kg,将近10kg,占全过程的一半,所以初始状态误差的影响较大;第Ⅱ阶段,主要为拖曳控制,防碰撞燃料为4kg,面内防缠绕控制为3.0kg,面外摆角控制为0.6kg;第Ⅲ阶段,防碰撞燃料为4.5kg,面内防缠绕为0.05kg,面外摆角控制为0.01kg。
由仿真算例可以看出,准霍曼拖曳离轨过程是稳定可控的,50%的燃料消耗量约11kg用于拖曳过程的防碰撞、防缠绕控制。但如果喷气力较小,只有50N,数值仿真是不稳定,所以脉冲喷气拖曳控制稳定的必要条件是喷气力不能过小,具体与绳系组合体的质量、初始扰动有关,可经数值仿真确定。
4 总结
推导了空间绳网应用中绳系组合体的拖曳离轨空间运动动力学模型,提出了准霍曼拖曳离轨的脉冲控制策略和方法,给出了拖曳非线性系统系统稳定控制的措施(增设缓冲弹簧及保证足够的喷气力)和同步轨道拖曳离轨的燃料消耗量,各控制参数由数值仿真决定。
[1] Cartmell M D, McKenzie D J. A review of space tether research[J]. Progress in Astronautical Sciences, 2008, 44(1):1-21.
[2] Heinen G, Smith F, Santangelo A, et al. An orbit transfer vehicle utilizing an electrodynamic tether[J]. Astronautical Sciences Meeting & Exhibit, 2000, 6(64):75-77.
[3] Kmnar K, Pradeep S. Strategies for three dimensional deployment of tethered satellites[J].Mechanics Research Communications, 1998, 25(5):543-550.
[4] Steindl A, Troger H. Optimal Control of Deployment of a Tethered Subsatellite[J]. Nonlinear Dynamics, 2003, 31(3):257-274.
[5] 王维. 绳系卫星的动力学与控制[D]. 北京:清华大学,2009.
[6] 文浩. 绳系卫星释放和回收的动力学控制[D].南京:南京航空航天大学, 2008.
[7] 朱仁璋. 速率控制下的空间系绳的伸展[J].中国空间科学技术,1991, 11(4):50-55.
[8] 黄奕勇,杨乐平. 改进的绳系卫星系统距离速率控制律[J].上海航天,2007, 24(3):30-33.
[9] 顾晓勤. 圆及椭圆轨道释放绳系子星的方法研究[J].空间科学学报,2002, 22(3):282-288.
[10] 顾晓勤. 绳系卫星释放及工作态动力学分析[J].空间科学学报,2002,22(2):154-162.
[11] 崔乃刚,刘墩. 基于椭圆轨道的绳系卫星伸展及释放过程仿真研究[J].哈尔滨工业大学学报,1996, 28(4):117-122.
[12] 于绍华. 空间系留卫星系统动力学与控制[J].宇航学报,1992, 13(2):87-94.
[13] ROGER-Team. RObotic GEostationary Orbit Restorer ROGER Phase A Executive Summary. 2003,10.
[14] Liu H T, Yang L P. An investigation on tether-tugging de-orbit of geostationary satellites[J]. Science China Technology,2012,55(7):2019-2027.
[15] 王道吉. 绳网展开动力学与拖曳变轨研究[D]. 长沙:国防科学技术大学,2012.
[16] 刘新建,刘海涛,王道吉. 绳网展开动力学研究报告[D]. 长沙:国防科学技术大学,2012.
[17] 刘新建,郑杰匀. 绳网组合体拖曳变轨动力学与控制研究报告[D].长沙:国防科学技术大学,2014.
Modeling of Tug Deorbit and Feasibility of Pulse Jet ControlStrategy for Tether-Combined System
LIU Xin-Jian Zheng Jie-Yun
(College of Astronautical Science and Engineering, National University of Defense Tech., Changsha 410073, China)
For the motion control of tug deorbit of a tether combined system of rope net in space, tether tension control needs a set of windlass, tension force measurement and control, which will increase the weight, complexity and cost, and decrease operation reliability. It has been put forward that the 3-axis orthogonal nozzles fixed in tug vehicle can be used to simultaneously realize relative motion control between tug boat and target, and centre-of-mass control of system orbital motion, but tether tension is only restricted, the three dimensional space motion dynamic model of combined system has been deduced, a quasi-Hohmann tug deorbit method has been given and verified to be feasible by numerical simulation with an example of geostationary tug deorbit, and jet force and fuel consumption has been given, which may be referential for the research of space net.
Space net; Tether combined system; Tug deorbit dynamics; Pulse jet control
2017-03-18;
2017-04-21
刘新建(1966-),男,博士,主要从事飞行器设计与控制研究。E-mail:lxjxyy@126.com
V433
A
2096-4080(2017)01-0013-08

