液氢空化流动特性研究

王国玉，陈泰然，黄 彪，潘俊屹

(北京理工大学机械与车辆学院，北京 100081)

液氢空化流动特性研究

王国玉，陈泰然，黄 彪，潘俊屹

(北京理工大学机械与车辆学院，北京 100081)

对液氢空化流动的实验数据进行了统计分析，数值计算了大范围温度变化下液氢空化流动的变化特征。结果表明采用的数值计算方法计算结果与实验数据吻合良好。随着温度变化，液氢空化流动存在两种空化行为。当温度低于转捩温度时，空化行为的变化受液/汽密度比控制，空穴面积随温度的增加而增加；当温度高于转捩温度时，空化行为的变化热力学效应控制，空穴面积随温度的增加而减小。空化数和来流速度越大，转捩温度越高。

液氢；空化流动；转捩温度

0 引言

航空航天事业的高速发展对运载工具的推力、功率密度和可靠性提出了越来越高的要求，液体火箭发动机正是当前大运载的主力军。由于发动机元件的设计受到尺寸和重量的限制，提高推力就需要尽可能提高涡轮泵的功率密度，这对涡轮泵的空化性能提出了严苛的要求，空化条件也一直是涡轮泵设计的主要限制条件之一[1]。常温水体中的空化相变过程通常被假设为等温过程[2]。然而，由于热流体较小的液/汽相密度比和相变过程中显著的温度变化，等温假设对于热流体空化而言则不再成立[3]。液体火箭发动机所用的液氢和液氧等燃料就是典型的热流体。研究表明[4]，诱导轮内部液氢的非定常空化流动显著影响诱导轮的性能，同时液氢空化的热力学效应影响显著，从而改变了诱导轮内部的流动特征。更加精确地描述强热力学效应作用下液体火箭发动机燃料的空化流动特性对液体火箭发动机的性能提升具有重要意义。

液氢和液氧等低温流体的空化流动实验研究[5]，对设备要求较高，花费较大，且危险系数高。目前只有NASA的研究人员Hord[6]在1973年做了最为完整的针对液氢和液氮的空化流动实验，该实验对认识低温流体的空化流动特征提供了重要参考，也一直是发展数值计算方法的验证指标。近年来，随着计算机水平的提高，空化流动的数值计算方法发展迅速。空化模型在空化流动的数值计算中扮演着重要的角色，计算中通常假设汽液混合相为均质，然后利用正压状态方程模型或相间质量传输方程模型来模拟两相区域内的变化。在正压状态方程模型中，混合物的密度由状态方程确定，即混合区密度是压力与温度的函数。Rapposelli等[7]基于正压状态方程模型计算了液氮和液氧绕对称回转体和二维翼型的空化流场，利用正压方程来计算空化流中的密度场，无法捕捉到斜压矩的产生，尤其是没有考虑相间质量传输，无法解释空化过程的对流和输运，因而无法反映相变造成的热力学效应的影响机制。相间质量传输方程模型根据蒸发和凝结源项来调节空化区域的质量传输，可以真实反映由于相变造成的当地温度的变化。Hosangadi等[8-9]基于相间质量传输模型，在全流场内求解了能量方程，并耦合了流体介质物质属性的变化，预测的绕翼型的压强和温度与实验结果吻合良好。Utturkar等[1]采用基于界面捕捉空化模型来捕捉空化区域的变化，结果证明，翼型头部温度与实验吻合较差。

空化流动是一种强烈的湍流流动，因此湍流模型的选择对于模拟空化流动尤为重要。现有的基于雷诺时均化(RANS)的湍流模型存在对空化区域湍流黏性过预测的问题[10-12]，无法准确预测空化流动的非定常发展过程。近来发展的大涡模拟(LES)则可以很好地预测空化流动的非定常行为，但对计算资源要求较高[13-15]。因此，在现有湍流模型的基础上发展了一系列混合模型，如基于密度修正的湍流模型(DCM)[11-12]、局部时均化湍流模型(PANS)[16]和滤波器湍流模型(FBM)[17]。

虽然国内外研究人员已经对液氢等低温流体的空化流动特征开展了大量的实验研究工作，但由于实验条件限制，对于大范围温度变化条件下(尤其在三相点附近温度)液氢的空化流动特性的变化还不十分清楚。

本文首先对Hord[6]完成的液氢绕轴对称回转体的空化流动实验数据进行了统计处理，分析了在不同温度、速度和空化数下空穴变化的特征。然后应用基于传热修正的相间质量传输模型和大涡模拟湍流模型，在求解连续方程、动量方程、质量输运方程的同时耦合能量方程，计算了液氢绕轴对称回转体的空化流动。通过与实验数据对比验证了数值计算方法的准确性，然后计算了大范围温度变化条件下液氢空化流动的变化特征，为解决工程中诱导轮内部低温介质的空化问题提供了重要参考。

1 控制方程及数值计算方法

1.1 控制方程

均质多相流假设下空化流动的基本控制方程包括连续性方程、动量方程、能量方程和质量方程，在笛卡儿坐标下可以表示为：

(1)

(2)

(3)

(4)

ρm=ρl(1-αv)+ρvαv

(5)

μm=μl(1-αv)+μvαv

(6)

其中，ρm为混合密度,ρl和ρv分别为液相和汽相的密度,U为速度,p为压力,μm为混合黏度,μl和μv分别为液相和汽相的动力黏度,μtur为湍流黏性系数,f为质量分数,Lev为蒸发潜热,h为比焓,Prtur和Prlam分别为湍流和层流普朗特数,αl和αv分别为液相和汽相的体积分数.

方程(4)中的m+和m-分别表示凝结和蒸发源项. 基于传热修正的相间质量传输模型可以表示为[3]：

(7)

(8)

(9)

其中，M为摩尔质量,Rv为气体体积常数,T为当地温度，pv为饱和蒸汽压.C1= 0.13，C2= 0.01 为经验系数，该经验系数已在绕水翼和收缩扩张流道内的空化流动计算中得到验证[3,20-21]，因此本文直接采用。气泡半径rb根据单泡壁面传热过程推导而来[3]，其中,Lev为蒸发潜热,t∞为参考时间(根据特征长度和流动速度计算而来), ΔT为当地温度变化,λl为液相热扩散率,Cl为液相比热容。

字际关系指字与字因来源或使用场景而产生的关系，包括古今字、异体字、繁简字关系等。古代汉语与现代汉语中的字际关系不尽相同，同一个字记录的词语也有所不同。古代汉语中两个音义不同的字，在现代汉语中可能“归并”为同一个字。如“后”与“後”，在古代汉语中迥然有别，但在现代汉语中“後”被废除，“后”一身而兼二义。整理古籍时，我们不能拿现代汉字的文字体系来对应古代汉字的文字体系。特别是繁体字整理本，应尽量保留古籍的用字原貌，不能对古籍用字妄加臆改，或者对字际关系视而不见。

1.2 大涡模拟湍流模型

本文采用大涡模拟对湍流进行处理，控制方程如下：

(10)

式中亚格子应力τij定义如下：

τij=UiUj-UiUj

(11)

采用Smagorinsky 模型[18]对亚格子应力进行处理

(12)

其中，Sij为大尺度应变量张量，亚格子黏性νSGS通过以下方法处理

(13)

本文中计算域与边界条件设置与Hord[6]实验保持一致，考虑到计算的经济性，将轴对称回转体模型简化为二维，计算域及边界条件如图1(a)所示。本文所采用的二维计算域存在一定误差，但其可行性已在相关文献中得到验证，并不影响本文对液氢空化流动特性的分析[22-23]。为了更准确地反映空化流动细节特征并满足大涡模拟计算要求，如图1(b)在回转体近壁面周围进行了网格加密，并确保近壁面第一层网格的y+值在1左右，满足壁面函数的要求。边界条件采用速度入口和压力出口并在边界处设置了温度和相分布，流动区域上下边界为自由滑移壁面条件，回转体表面采用绝热、无滑移壁面。

为了验证计算网格，图2给出了349B工况[6]下实验数据与不同网格计算得到的温度和压力对比图，边界条件与Hord实验[3]保持一致。从图中可以看出，本文采用的数值计算方法能基本描述液氢绕对称回转体流动中温度和压力分布，与实验数据基本一致。在空穴产生的区域内，温度和压力降低，在空穴溃灭的区域，温度略有升高，这与热力学效应对空化的影响效果是一致的。图中显示两种网格数值计算结果与实验均比较接近，因此在后续的计算中采用网格数较小的网格进行计算，网格总数为1.1×105。

2 结果与讨论

2.1 液氢非定常空化流动特征

为直观显示液氢空化流动的非定常演化过程，图3给出了考虑热力学效应和等温条件下空穴发展过程，两种条件下均以0.2tcycle(tcycle为空化发展周期)为时间间隔来展示动态演化过程。从图中可以明显看到，两种条件下的空穴均为附着型空穴，均在回转体前缘生长并逐渐向后发展，最后发生脱落。然而，在不同条件下，液氢非定常空化流动的特征也存在很大不同。在考虑热力学效应条件下，空穴内部大部分区域的气体含量少于55%，最大能达到80%；而在等温条件下，空穴内大部分区域的气体均达到了90%，最大为95%，且等温条件下的空穴面积明显更大。结合图2(a)可以看出，在考虑热力学效应条件下，液氢蒸发吸热使得当地温度降低，从而改变了当地液氢的物质属性，当地饱和蒸汽压降低意味着当地空化数的升高。说明热力学效应抑制了液氢空化的发展，这是液氢空化较常温水体空化最显著的区别。进一步分析可以看出，在考虑热力学效应条件下，空穴内外的温度梯度和压力梯度均明显减小，空穴变得模糊，发展的尺度和程度均比等温条件有所减小。显然，耦合了能量方程的算法更能真实反映液氢空化过程，与实验结果更为吻合。

2.2 温度变化对液氢空化流动的影响

上文分析了热力学效应对液氢空化流动的显著影响，接下来通过对Hord[6]完成的实验数据进行统计处理，分析在不同温度、速度和空化数条件下空穴变化的分布。图4给出了基于实验数据拟合得来的不同来流条件下的空穴长度分布，图中黑点为实验数据点。每幅图中的数据均保证了相近的来流速度，从而得到在相同来流速度条件下不同空化数和温度对空穴长度的影响。图4(a)和图4(b)中空穴面积的变化呈现相同的规律，在同一来流温度下，空化数越大则空穴长度越小；在空化数相等的情况下，温度越高则空穴长度越小。这与上文讨论的热力学效应带来的影响是相符的。随着来流速度进一步提高，如图4(c)和图4(d)所示，空穴长度的整体变化基本保持不变。然而，在来流温度为22.5K附近，出现了随着温度增加空穴长度不变甚至增加的区域，这就出现了所谓的“反热力学效应”区域。液氢空化流动中的“反热力学效应”现象与高温水体中观测得到的结果一致[3,19]，然而此前并未报道过。

为了进一步分析温度变化对液氢空化流动的影响，本文通过数值计算得到了不同流动条件下的空化流动变化。图5给出了空化发展10个准周期内无量纲空穴平均面积随温度的变化。从图5(a)中来流速度U∞=63.9m/s的工况可以看出，在该工况下空穴面积随着来流温度增加单调减小；而对于来流速度U∞=90m/s的工况，空穴面积随着来流温度增加出现了先增后减的变化过程。结合高温水体的分析结果[3]和液氢的物质属性变化，认为当液氢的温度接近其三相点时，空化的热力学效应并不十分显著，此时液/汽相的密度比主导了空化的行为。随着温度的增加，液/汽相密度比逐渐减小，空穴内部的小气泡直径变小，空穴形态变得模糊，空穴内部的小碎泡以更快的速度聚合并向下游移动，从整体上造成了空穴面积的增加。随着温度的进一步增加，液氢空化的热力学效应显著增加，液相蒸发吸热使得当地温度降低，空穴区域内温度的降低使得液相的饱和蒸汽压降低，饱和蒸汽压降低意味空化更难发生，这就是空化热力学效应抑制空化发展的基本过程。因此，对于σ∞=0.38，U∞=90m/s的工况，空化行为转变的转捩温度在16K左右。进一步分析空穴面积在大空化数下的变化(如图5(b)和图5(c)所示)，可以发现空化数越大，则转捩温度越高，说明空化数越大空化热力学效应越弱。对比不同速度下空穴的变化可以发现，来流速度增加使得空化流动惯性力增加，从而削弱了热力学效应对空穴的影响。因此，在相同空化数下，来流速度越大，转捩温度越高。

本文的研究工作为诱导轮的设计研制工作提供了重要参考。工程中应该根据诱导轮的性能需求，合理设置液氢温度、入口压力、流量和诱导轮转速的分配，避免诱导轮的运行工况在转捩温度附近运行。

3 结论

本文首先对液氢绕轴对称回转体的空化流动实验数据进行了统计处理，分析了在不同温度、速度和空化数下空穴变化的特征。然后应用基于传热修正的相间质量传输模型和大涡模拟湍流模型，在求解连续方程、动量方程、质量输运方程的同时耦合能量方程，计算了大范围温度变化条件下液氢空化流动的变化特征，本文主要结论有以下几点：

1)本文采用的数值计算方法计算结果与实验值吻合良好，能够较准确地预测液氢绕回转体空化流动的非定常演变过程，准确反映热力学效应对液氢空化流动的影响。

2)随着温度的变化，液氢空化流动存在两种不同的空化行为，空化行为转变所对应的温度为该工况下的转捩温度。当温度低于转捩温度时，空化行为的变化受液/汽相的密度比控制，空穴面积随着温度的增加而增加；当温度高于转捩温度时，空化行为的变化热力学效应控制，空穴面积随着温度的增加而减小。

3)在其他流动条件不变的前提下，空化数和来流速度越大，则转捩温度越高。

4)工程中应根据诱导轮的性能需求，合理设置液氢温度、入口压力、流量和诱导轮转速的分配，避免诱导轮在转捩温度附近运行。

[1] Utturkar Y, Wu J, Wang G, et al. Recent progress in modeling of cryogenic cavitation for liquid rocket propulsion[J].Progress in Astronautical Sciences, 2005, 41(7): 558-608.

[2] 张博,王国玉,黄彪,等.云状空化非定常脱落机理的数值与实验研究[J].力学学报,2009, 41(5):652-658. Zhang Bo, Wang Guo-yu, Huang Biao, et al. Numerical and experimental studies on unsteady shedding mechanisms of cloud cavitation[J].Chinese Journal of Theoretical and Applied Mechanics,2009,41(5):652-658(in Chinese).

[3] Chen T, Huang B, Wang G.. Numerical study of cavitating flows in a wide range of water temperatures with special emphasis on two typical cavitation dynamics[J].International Journal of Heat and Mass Transfer, 2016, 101: 886-900.

[4] Hosangadi A, Ahuja V, Ungewitter R J, et al. Analysis of thermal effects in cavitating liquid hydrogen inducers[J].Journal of Propulsion and Power, 2007, 23: 1225-1234.

[5] Franc J, Rebattet C, Coulon A. An experimental investigation of thermal effects in a cavitating inducer[J].Journal of Fluids Engineering,2004, 126: 716-723.

[6] Hord J. Cavitation in liquid cryogenics[R].III-Ogive, NASA-CR-2242,1973.

[7] Rapposelli E, d’Agostino L. A barotropic cavitation model with thermodynamic effects[C].Fifth International Symposium on Cavitation, Osaka, Japan, 2003: 1-9.

[8] Hosangadi A, Ahuja V. Numerical study of cavitation in cryogenic fluids[J].Journal of Fluid Engineering,2005,127:267-281.

[9] Hosangadi A, Ahuja V, Ungewitter R J, et al. Numerical study of a flat plate inducer: comparison of performance in liquid hydrogen and water[C].Proceedings of the 42ndAIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Sacramento, CA, United States,2006:7210-7222.

[10] Reboud J L, Stutz B, Coutier O. Two phase flow structure of cavitation:experiment and modeling of unsteady effects[C]. 3rdInternational Symposium on Cavitation (CAV1998), Grenoble, France, 1998.

[11] Coutier-Delgosha O, Fortes-Patella R, Reboud J L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J].Journal of Fluids Engineering,2003, 125 (1):38-45.

[12] Huang B, Dudoin A, Young Y L. Physical and numerical investigation of cavitating flows around a pitching hydrofoil[J].Physics of Fluids, 2013,25 (10): 102109.

[13] Wang G, Ostoja-Starzewski M. Large eddy simulation of a sheet/cloud cavitation on a NACA0015 hydrofoil[J].Applied Mathematical Modelling,2007, 31 (3):417-447.

[14] Ji B, Luo X W, Arndt R E A, et al. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil[J].International Journal of Multiphase Flow,2015,68: 121-134.

[15] Huang B, Zhao Y, Wang G. Large eddy simulation of turbulent vortex-cavitation interactions in transient sheet/cloud cavitating flows[J]. Computers & Fluids, 2014, 92 (3) :113-124.

[16] Ji B, Luo X, Wu Y, et al. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil[J]. International Journal of Multiphase Flow, 2013, 51(5):33-43.

[17] Wu J Y, Wang G Y, Shyy W. Time-dependent turbulent cavitating flow computations with interfacial transport and filter-based models[J].International Journal for Numerical Methods in Fluids,2005, 49 (7): 739-761.

[18] Smagorinsky J. General circulation experiments with the primitive equations[J].Monthly weather review, 1963, 91(3): 99-164.

[20] Liu S, Li S, Zhang L, et al. A mixture model with modified mass transfer expression for cavitating turbulent flow simulation[J].Engineering Computations,2008,25 (4): 290-304.

[21] Liu D M, Liu S H, Wu Y L, et al. A thermodynamic cavitation model applicable to high temperature flow[J].Thermal Science, 2011, 15(suppl. 1):95-101.

[22] Zhu J, Zhao D, Lu X,et al. Interactions of vortices, thermal effects and cavitation in liquid hydrogen cavitating flows[J].International Journal of Hydrogen Energy, 2016, 41(1):614-631

[23] Long X, Liu Q, Ji B. Numerical investigation of two typical cavitation shedding dynamics flow in liquid hydrogen with thermodynamic effects[J].International Journal of Heat and Mass Transfer,2017, 109: 879-893.

Characteristics of Hydrogen Cavitating Flows in a WideRange of Free-stream Temperature

WANG Guo-yu, CHEN Tai-ran, HUANG Biao, PAN Jun-yi

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

In this paper, the experimental data of liquid hydrogen cavitating flow are statistically analyzed, and the characteristics of liquid hydrogen cavitating flow under a wide range of temperatures are numerically investigated. The results show that the calculated results are in good agreement with the experimental data. As the temperature changes, there are two kinds of cavitation behavior in liquid hydrogen. The change of the cavitation behavior is dominated by the liquid/vapor density ratio when the temperature is lower than the transition temperature, and the cavity area increases with the increasing temperature. When the temperature is higher than the transition temperature, the thermodynamic effects dominate cavitation behavior, and the cavity area decreases with the increasing temperature. Moreover, the transition temperature increases with the increasing cavitation number and free-stream velocity.

Hydrogen; Cavitating flows; Transition temperature

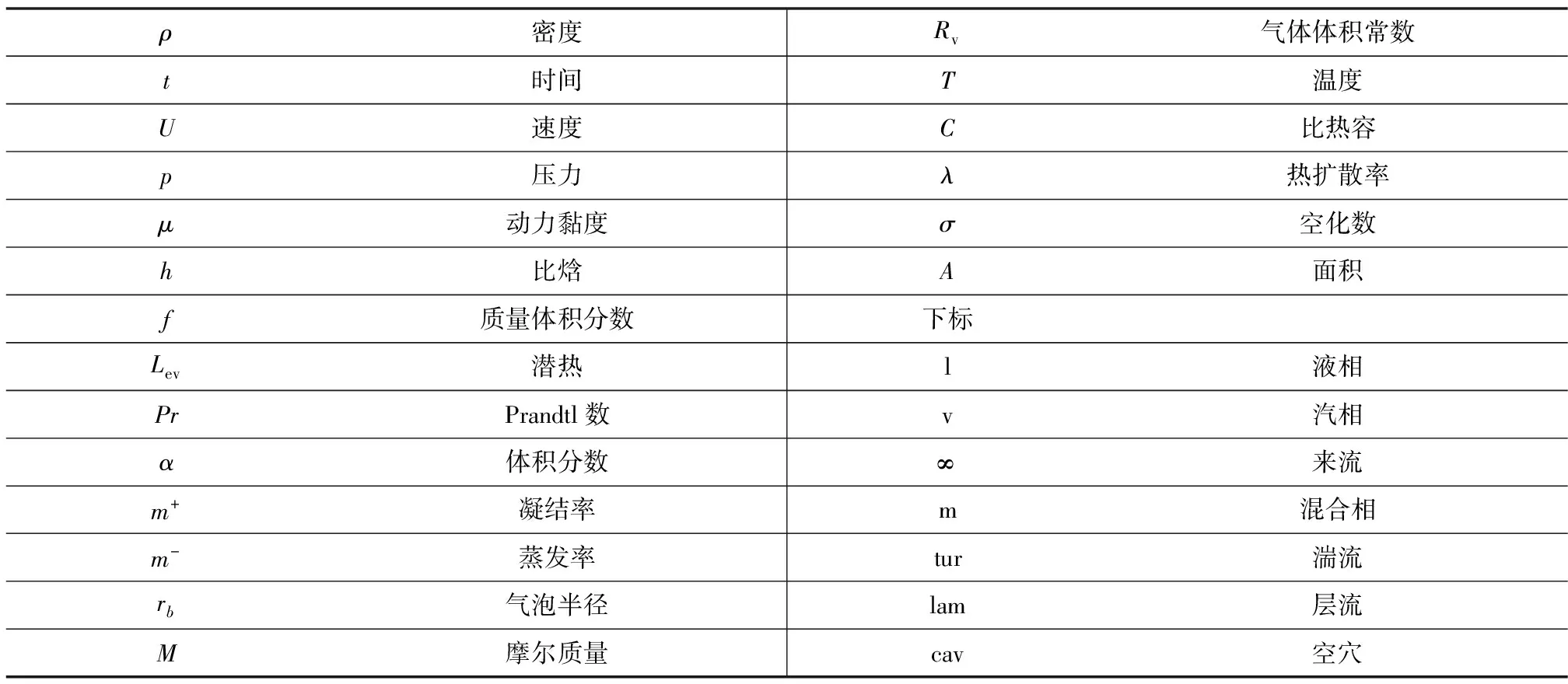
符号表

2017-03-16；

2017-04-21基金项目：国家自然科学基金(51479002)

王国玉(1961-)，男，教授，博导，主要从事空化与水动力学研究。E-mail:wangguoyu@bit.edu.cn

V419

A

2096-4080(2017)01-0027-07