弹性体运载火箭建模及控制器设计
韦常柱,琚啸哲,张 亮,崔乃刚
(哈尔滨工业大学航天学院,哈尔滨 150001)
弹性体运载火箭建模及控制器设计
韦常柱,琚啸哲,张 亮,崔乃刚
(哈尔滨工业大学航天学院,哈尔滨 150001)
考虑运载火箭飞行过程中的弹性振动特性,对运载火箭进行全量动力学建模以及控制器设计。首先将运载火箭考虑为一维梁模型并建立全量动力学模型,分别引入自适应滤波姿态控制算法和H2范数鲁棒增益调度控制算法设计控制器。仿真结果表明:在考虑舵机非线性情况下两种控制方法均能够满足精度要求,在具有较大外部扰动情况下,鲁棒增益调度控制算法相较于自适应滤波算法具有较强的鲁棒性。
运载火箭;刚弹耦合;自适应滤波;H2范数鲁棒增益调度控制
0 引言
运载火箭作为当代航天活动中不可或缺的运载工具,其控制系统性能是影响发射任务成功与否的关键性因素。由于运载火箭自身具有大长细比、箭体结构强度不高、箭体固有频率较小等特点,因而呈现出明显的弹性特征。在无控飞行过程中,较大振幅的弹性振动不仅会对运载火箭结构和内部仪器产生破坏,而且弹性振动信号也将通过传感器影响刚体控制器的控制精度,同时气弹耦合和刚弹耦合等问题也将对运载火箭的姿态运动稳定性产生重要影响,从而导致发射任务失败[1]。因此,弹性振动抑制技术是大长细比运载火箭控制系统设计中的一项极为关键的技术。
国内外针对弹性体运载火箭的姿态控制系统设计方法已有了一部分研究成果。为实现弹性运载火箭的高精度姿态控制,王青等[2]提出了一种新型的2阶滑模变结构控制方案,并利用超螺旋算法推导了控制律。周军等[3]将鲁棒状态观测器应用到运载火箭姿态稳定控制中,通过对复合干扰的观测补偿,实现了抗干扰的姿态控制器设计。赵小平等[4]基于自适应鲁棒控制方法设计了重型运载火箭的姿态控制器,讨论了对弹性振动的抑制作用,并利用参数投影技术解决了自适应控制器在工程中的可实施性问题。基于滑模控制策略,王子瑞[5]设计了运载火箭三通道姿态滑模控制器,并利用扩张状态观测器实现了外部复合扰动的观测和补偿,通过仿真验证了控制器的有效性。Choi等[6]结合自适应频率辨识方法和传统的PID控制算法设计了自适应姿态控制器,实现了对弹性振动的抑制和姿态的稳定控制。
本文针对弹性运载火箭的姿态控制问题,基于一维梁模型建立了运载火箭的全量动力学模型,分别设计了基于SMM[7]频率辨识的自适应姿态控制器和H2范数鲁棒变增益调度控制器。最后针对两种控制方法分别进行仿真分析,验证两种控制方法的有效性以及鲁棒性,比较了两种方控制方法的优缺点。
1 运载火箭全量动力学建模
运载火箭一般具有较大的长细比、较小的结构质量/燃料质量比等特征,所以结构强度较弱,在外力作用下极易产生弹性振动。如果火箭的弹性振动不能很快衰减,而是等幅振荡甚至发散,不仅会使箭体结构强度受到破坏,而且对姿态稳定极为不利。因此,需要首先开展弹性运载火箭的全量动力学建模,为后续控制提供基础。
针对运载火箭的整体弹性变形特征,通常采用两端自由的空间一维梁模型来模拟,其弹性振动一般只考虑梁扭转振动、俯仰方向的弯曲振动和偏航方向弯曲振动,对应的广义坐标形式的振动微分方程为:
(1)

基于弹性振动方程可推导获得运载火箭全量动力学模型如下所示:
(2)
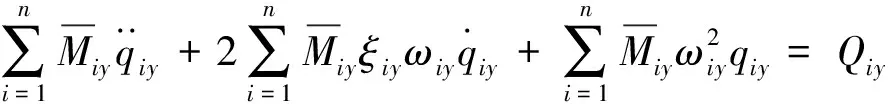
(i=1,2,…,n)
(i=1,2,…,n)
(3)
2 弹性运载火箭控制器设计
针对运载火箭飞行过程中存在的弹性振动抑制问题,在对全量动力学模型进行小扰动线性化的基础上,分别设计自适应滤波控制器和H2范数鲁棒变增益调度控制器。
2.1 运载火箭小扰动线性化模型
由于运载火箭全量动力学模型为一组多维非线性、变系数微分或代数方程,无法直接用于稳定性分析和姿态控制系统设计,因此需要基于小扰动线性化方法。首先将弹性运载火箭全量动力学模型进行泰勒展开,忽略其运动状态小量,即可以获得三通道独立的线性化模型。
以俯仰通道为例,线性化模型如下所示:
(4)
2.2 自适应滤波控制器设计
自适应滤波控制方法结合了PID控制算法和自适应滤波算法,在一般刚体PID控制基础上通过自适应频率辨识的陷波器对弹性振动信号进行补偿,从而对低阶弹振频率附近进行相位校正,实现稳定控制。
自适应滤波控制结构如图1所示,其控制器的输出信号在经过陷波器处理后送至执行器,而陷波器则通过自适应频率辨识算法调节自身的陷波频率,因此具备处理一定频率范围内振动信号的能力。
2.2.1 刚体PID控制器设计
运载火箭刚体PID控制器需要根据标准弹道特征点处小扰动线性化后的刚体动力学模型进行设计。以俯仰通道为例,由公式(4)可得,在忽略弹性振动方程和发动机摆动惯性力及力矩条件下有:
(5)
经过拉普拉斯变换,可得传递函数如式(6)所示:
(6)
令
(7)
则俯仰通道控制系统结构为:
利用根轨迹方法可对PID参数进行设计,然后通过线性插值实现对全主动段飞行弹道上的刚体稳定控制。
2.2.2 自适应陷波器设计
火箭弹体的弹性振动对姿态稳定控制系统的影响主要是通过安装在弹体上的陀螺敏感元件引入的,姿态角敏感器和姿态速率陀螺测量关系表达式为:
(8)
可见,进入控制系统并引起控制性能变化的即为弹性振动信号,因此设计自适应陷波器滤除弹振信号是十分必要的。
假设待处理的信号具有如下形式:
(i=1,2,…,m)
(9)
为了辨识待处理信号的ωi值,可以采用如下形式的滤波器:
将y(n)作为滤波器的输入信号,问题可转化为寻找参数ai的一个优化过程,即当ρ→1时,有:
因此,滤波器的输出ε(n)→e(n),从而实现对多个频率正弦信号的滤波。滤波器系数采用Steiglitz-mcBride方法进行辨识,该算法能够在理论上证明其解的收敛性且收敛迅速,计算量小,基本迭代过程如下:

es(n)=g(n-Δ+1)+ρ2mg(n-2m-Δ+1)-
λ=λrλ+(1-λr)λ∞
ρ=ρrρ+(1-ρr)ρ∞
(10)
至此,自适应滤波器已经设计完毕,基本框图如下所示:

2.3H2范数鲁棒变增益调度控制器设计
变增益调度控制器在一般设计过程中需要划分工作区间,选择大量的特征点进行控制器设计,并通过插值方式实现全局控制。此设计方法在工程上应用较多,但全局稳定性和鲁棒性难以得到保证。考虑算法的计算复杂度和全局稳定性,选择了鲁棒变增益调度控制算法进行控制器的设计。
首先将运载火箭小扰动线性化动力学模型表述为如下形式:
z(t)=Cx(t)
(11)
其中,h、v为参变量。系统矩阵A(h,v)随着参变量变化而变化,C矩阵为对角单位矩阵。此时,动力学模型为以h、v为变参量的参数依赖LPV模型,经过简单转化即可变为多胞形系统。
为了消除控制系统的稳态误差,对动力学模型进行变形,引入x(t)的积分量作为附加状态量[10],此时增广动力学模型变为:
(12)
其中,
考虑系统存在外部扰动w(t),外部扰动的输入矩阵取为E1。以扰动向被调输出的输入输出传函的H2范数作为控制器的性能指标。引入如下定理[11]:
针对如下所示的多胞形系统
z(t)=Cx(t)+Du(t)
首先设计全状态反馈控制律u=Kx,如果所有多胞形顶点处的状态空间系统均满足以下线性矩阵不等式:
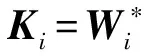
Trace(Z)<γ2
(13)
基于上述定理,使用LMI工具箱对不等式组(13)进行求解,则H2范数鲁棒增益调度控制器即可完成设计。
3 仿真分析
3.1 自适应陷波控制器仿真结果与分析
基于小扰动线性化模型首先进行刚体PID控制器设计与仿真,在不考虑弹性振动情况下对运载火箭30s主动段飞行过程进行控制仿真,以俯仰通道为例,仿真结果如下所示:
从图4可以看出,在不考虑弹性振动情况下,刚体PID控制器能够进行很好的姿态控制,仿真过程中最大姿态跟踪误差小于2°,且稳态跟踪误差小于0.1°,控制性能良好,验证了在不考虑弹性振动情况下刚体PID控制器的有效性。
考虑运载火箭弹性振动,将弹振信号加入运载火箭模型中,选择第30s飞行特征点进行分析,仍采用刚体控制器,单位阶跃输入信号作用下系统的跟踪误差曲线如图5所示。
从图5中可以看出,在不引入陷波器时,仅仅依靠刚体控制器无法有效控制运载火箭的弹性振动,姿态角始终存在小幅抖振现象,可能会给运载火箭结构带来难以预料的破坏。
为了抑制弹振信号,基于SMM算法设计自适应陷波器,SMM算法的初始参数设置为:
λ=0.7,λr=0.99,λ∞=0.995
ρ=0.7,ρr=0.99,ρ∞=0.995
κ=1
P(1)=κI
h(n)=g(n)=0
选取第30s飞行特征点进行分析,引入陷波器后单位阶跃输入信号作用下系统跟踪误差曲线如图6所示。
从图6可以看出,引入陷波器后,姿态角抖振消失,证明了自适应陷波器能有效滤除运载火箭飞行过程中的弹振信号。
3.2 鲁棒变增益调度控制器仿真结果与分析
利用LMI工具箱对多胞形顶点的鲁棒增益调度控制器进行求解。对方案弹道飞行包线高度极限值和速度极限值对应的4个顶点分别求取反馈矩阵K1、K2、K3、K4。基于凸分解原理对反馈矩阵进行线性组合并进行仿真,仍以俯仰通道为例,非线性舵条件下鲁棒增益调度控制结果如图7所示。
从图7可以得出,在不考虑外部扰动以及结构不确定性情况时,鲁棒增益调度控制作用下运载火箭飞行过程中俯仰姿态跟踪误差小于2°,且稳态跟踪误差小于0.1°,能对程序角实现很好的跟踪。
3.3 鲁棒变增益调度控制器仿真结果与分析
考虑飞行过程中大气环境复杂,为模拟真实飞行环境,在仿真过程中对气动力和气动力矩附加15%的随机扰动,以俯仰通道为例,两种控制器的仿真结果如图8所示。
分析图8可知,在存在较大外部扰动情况下,鲁棒增益调度控制器仍然能够实现较高精度的姿态跟踪,程序角跟踪误差小于2°;而自适应滤波控制器作用下运载火箭难以保证对程序姿态角的有效跟踪,相对于无扰动和结构不确定情况下控制性能有所降低,体现了鲁棒增益调度控制器比自适应滤波控制器具有更强的鲁棒性和抗扰性。
综合比较两种控制方法,在不考虑外部大扰动情况下,两者均可以满足弹性运载火箭的飞行控制精度要求;但是在应对外部大扰动时,鲁棒增益调度控制方法的鲁棒性更好。同时需要注意的是,在两种控制方法线下实现过程中,增益调度控制方法不需要对大量特征点进行线性化,计算复杂度低;线上实现过程中,增益调度方法仅需要对顶点反馈矩阵进行线性组合,工程应用性强。
4 结论
本文针对运载火箭飞行过程中弹性振动较为突出的特点,对运载火箭进行全量动力学建模,引入自适应陷波控制算法和鲁棒增益调度控制算法进行控制器设计。仿真结果表明,两种算法均能实现高精度的弹性运载火箭控制,在考虑大扰动情况下,鲁棒增益调度算法仍然能够满足运载火箭控制精度要求,展现了良好的鲁棒性。
[1] 孟中杰, 闫杰. 弹性高超声速飞行器建模及精细姿态控制[J]. 宇航学报, 2011, 32(8):1683-1687.
[2] 王青, 王昭, 董朝阳. 一种基于二阶滑模的柔性运载火箭姿态控制[J]. 系统仿真学报, 2009, 21(7):2006-2009.
[3] 周军, 水尊师, 葛致磊. 基于鲁棒状态观测器的运载火箭姿态控制系统设计[J]. 航天控制, 2012, 30(2):11-16.
[4] 赵小平. 基于自适应H_∞的重型运载火箭姿态控制方法研究[D]. 哈尔滨:哈尔滨工业大学, 2012.
[5] 王子瑞. 大推力运载火箭姿态控制的研究[D]. 武汉:华中科技大学, 2013.
[6] Choi H D, Bang H. An adaptive control approach to the attitude control of a flexible rocket[J]. Control Engineering Practice, 2000, 8(9):1003-1010.
[7] 刘昆, 孙平. 固体运载器姿态控制系统自适应滤波器设计[J]. 国防科技大学学报, 2010, 32(5):44-48.
[8] Zhu B L, Yang S X, Hu Y. Analysis of the elastic coupling between the control and body of a spinning rocket having high length to diameter ratio[J]. Journal of Beijing Institute of Technology, 2004, 24(7):587-591.
[9] Punchalard R. Mean square error analysis of unbiased modified plain gradient algorithm for second-order adaptive IIR notch filter[J]. Signal Processing, 2012, 92(11):2815-2820.
[10] Sun C, Huang Y, Qian C, et al. On modeling and control of a flexible air-breathing hypersonic vehicle based on LPV method[J]. Frontiers of Electrical and Electronic Engineering, 2012, 7(1):56-68.
[11] 俞立.鲁棒控制[M]. 北京:清华大学出版社,2002.
The Modeling and Controller Design forAeroelastic Rocket Launcher
WEI Chang-zhu, JU Xiao-zhe, ZHANG Liang, CUI Nai-gang
(Department of Aeronautics, Harbin Institude of Technology, Harbin 150001,China)
Modeling and controller designing for rocket launcher was carried out considering its elastic characteristic during the flight. Firstly a full variable dynamic model for the launcher was established based on the one dimensional beam, An adaptive filtering attitude controller and aH2norm robust gain-scheduled controller were introduced. Simulation results show that the both controllers perform well without neglecting actuators’ nonlinear characteristic, and the latter is of more robustness against large outer disturbance.
Elastic vibration; Full variable dynamic model; Rigid-elastic coupling; Adaptive filtering;H2norm Robust gain-scheduled control
2017-04-13;
2017-04-25基金项目:“上海市优秀学科带头人计划”资助项目(14XD1423300)
韦常柱(1982-),男,博士,哈尔滨工业大学航天学院副教授,主要从事飞行器制导与控制研究。E-mail:weichangzhu@hit.edu.cn
V448
A
2096-4080(2017)01-0021-06

