基于序列凸优化的高超声速滑翔式再入轨迹快速优化
赵党军,梁步阁,杨德贵,时 伟
(中南大学航空航天学院,长沙 410083)
基于序列凸优化的高超声速滑翔式再入轨迹快速优化
赵党军,梁步阁,杨德贵,时 伟
(中南大学航空航天学院,长沙 410083)
针对具有热流、动压、过载以及多个禁飞区约束的再入轨迹优化问题,提出采用序列凸优化方法快速求解。利用归一化时间作为自变量解决终端时间自由问题,并引入辅助控制变量以减少序列优化结果中的高频振荡,在此基础上,通过线性化、离散化和非凸约束的凸化处理,将非凸非线性优化问题转化为二阶锥规划(Second Order Conic Programming, SOCP)问题,然后采用凸优化求解算法快速求解。数值优化结果与对比验证表明该方法能快速高效求解多约束条件下的再入轨迹优化问题,且计算效率和性能均优于传统的非线性规划方法。
序列凸优化;再入轨迹优化;无损凸化;二阶锥规划
0 引言
升力式高超声速飞行器具有速度高、突防能力强等优点,近年来受到了国内外各相关领域的密切关注,出现了大量的研究成果[1]。与现有的亚声速/超声速飞行器相比,高超声速飞行器在近空间的稠密大气层内进行长时间、远距离飞行,其飞行轨迹必须满足热流、动压、过载等方面的约束。另外,考虑到敌方反导系统的探测、追踪以及拦截威胁,在飞行轨迹中还应考虑禁飞区约束,以避开敌方部署反导系统的区域。因此,飞行器轨迹规划是一个典型的强约束条件的动态优化问题[2]。
到目前为止,求解该类问题的方法总体来说可以分为两类:直接法和间接法[3]。所谓间接法主要源于庞特里亚金极大值原理,在状态变量基础上扩展协态变量获得哈密顿边值问题(Hamiltonian Boundary Value Problem, HBVP),通过一系列复杂的解析推导计算获得轨迹优化的解[4-5],这也使HBVP问题的求解异常复杂。为避免复杂的解析推导计算,间接法应运而生。间接法将无限维动态优化问题通过参数化技术转化为有限维的非线性规划(Nonlinear Programming, NLP)问题,然后通过序列二次规划(Sequential Quadratic Programming, SQP)[6]方法求解,如广泛使用的谱方法[7-10]就属于典型的间接法。目前,已经有一些较成熟的基于间接法的轨迹优化软件包可供使用,如GPOPS[9]、GPOCS[11]等。然而,SQP方法无法保证收敛速度,也无法保证必然获得全局最优解。在实际使用过程中,基于SQP方法的轨迹优化,对于初值异常敏感,且优化速度较慢。
与一般NLP方法相比,凸优化方法具有多项式时间复杂度,收敛速度快,且具有独特的理论优势——定义域内必然收敛,因此受到青睐。特别是在20世纪80年代,随着快速求解凸优化问题的内点法出现之后[12],凸优化方法开始进入很多工程优化领域。最近凸优化方法也开始用于求解轨迹优化这类复杂的非线性动态优化问题。文献[13-15]主要研究了带动力软着陆的轨迹优化问题,提出无损凸化处理方法,将非凸问题转化为凸优化问题,从而利用对偶内点法快速求解。类似于序列二次规划方法,Liu等给出了求解一般非凸非线性最优问题的序列凸优化算法[16],该算法采用轨迹线性化、离散化措施将非线性动态约束转化为凸约束,同时为保证线性化系统对原非线性系统的有效近似,增加了可信域约束。在此基础上,Liu将该方法用于再入轨迹优化之中[17]:在速度-攻角剖面已知条件下,以能量为自变量对原问题进行转化以避免终端时间自由问题;同时将热流、动压以及过载约束转化为速度-高度边界约束,在此基础上利用序列凸优化算法进行迭代求解获得再入最优轨迹。但以能量为自变量时,在飞行高度较高时,能量变化不显著,导致在高度大于65km时的轨迹无法进行离散化并优化。
针对上述问题,提出以归一化时间作为自变量,并选择泛化升力系数和倾侧角作为控制量,同时考虑多禁飞区约束,对高超声速飞行器再入轨迹优化问题的序列凸优化方法做出进一步改进:同时优化泛化升力系数和倾侧角两个控制变量,避免能量为自变量的缺陷。数值优化结果表明,本文所提方法是行之有效的。
1 问题描述
1.1 CAV再入运动模型

基于上述假设和关于泛化升力系数的定义,建立再入飞行器无量纲运动方程为[2]:
(1)
(2)
1.2 约束条件
再入过程中,CAV轨迹需满足一系列约束以保证飞行器安全。总体来说飞行约束分为等式约束和不等式约束。
(1)等式约束
根据事先确定的飞行器起点位置和目标位置,形成如下等式约束:
Φ[x(t0),x0]=0,Ψ[x(tf),xf]=0
(3)
值得注意的是,很多时候只指定了终端状态中的部分状态,如只规定了终端时的位置,也有可能只是规定了上下限,于是形成了不等式约束。
(2)不等式约束
不等式约束主要包括关于热流、动压和过载的约束
(4)
(5)
(6)
ρ=ρ0e-βReh
(7)
其中,h=(R-Re)/Re无量纲高度。为方便后续处理,对式(4)~式(6)进行归一化处理,得
≤03×1
(8)
其中,

(9)
除上述不等式约束外,施加于控制量上的限制也应考虑:倾侧角σ通常限制于某些特定区间(如[-π/3,π/3])以保证飞行稳定性;泛化升力系数λ因气动特性有所限制,因此有如下关于控制变量的约束
(10)
1.3 优化问题描述
综合考虑上述CAV运动模型以及相关约束条件,以时间最优为指标,CAV再入轨迹优化问题可以描述为
subject to: (2),(3),(8),(9),(10)
2 序列凸优化算法
2.1 问题重新描述

此外,若直接选择倾侧角σ和泛化升力系数λ作为控制变量,则会出现如文献[17]指出的控制量高频抖动现象,对飞行稳定不利,因此引入新的辅助控制变量,令
u1=λcosσ,u2=λsinσ,

(11)
控制约束可以改写为
(12)
同时,应保证式(13)的等式约束成立。
(13)
至此,问题 P0′与下面的问题P1等价。
P1:mint(1)
(14)
(15)
(16)
(17)
(18)
(19)
其中,(·)′=d/dτ,τ∈[0,1],约束(17)为不等式约束(8)和(9)的一般形式。问题P1中的指标函数J=t(1),表示为扩展状态t在终端时刻τ=1时的大小,即tf。显然,问题P0中的Lagrange项转化为问题P1中的Mayer项,成为一个线性函数,从而使得问题P1满足SOCP问题对于指标函数为凸函数的要求,且问题P1的解必然是问题P0的解。
2.2 线性化

(20)
为保证线性化系统式(20)合理逼近原系统式(15),状态及控制偏差应限制于可信域内,即
(21)
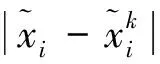
2.3 凸化处理
问题 P1中,路径约束式(17)和控制约束式(18)和式(19)都是非凸的,为使问题能用凸优化方法求解,必须对这些非凸约束进行凸化处理。
2.3.1 路径约束的凸化处理
路径约束式(17)中包含m个不等式约束,即
(22)

(23)
2.3.2 控制约束的凸化处理
由于辅助控制变量的引入,增加了关于控制量的等式约束式(19),显然该约束非凸,对其进行松弛处理,即将等式约束放宽为不等式约束
(24)

2.4 离散化

(25)
其中,j=0,…,N。重新排列并合并相同项,得
(26)
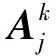
经过上述线性化、凸化以及离散化处理后,问题P1的最优解可以通过求解下面序列优化问题P2来进行求解。
P2:mint(1)
(27)
(28)
(29)

(30)
(31)
0≤u3≤4
(32)
-tan(σmax)u1≤u2≤tan(σmax)u1
(33)
(34)
其中,τ∈[0,1],(i=1,…,m,k=1,2,…)。可以证明经松弛处理后问题P2的解是原问题P1的解(参见文献[17])。
2.5 序列凸优化算法
显然,问题P2是SOCP问题,其目标函数为线性的,且各约束或者为线性函数,或者为二阶锥约束形式。如果选择足够小的离散化步长,SOCP问题P2的解与优化问题P1充分接近。求解问题P2的序列凸优化算法流程如下:

Step3:检查下面的收敛条件是否满足
(35)

3 数值优化结果
本文以CAV为例在MATLAB环境中进行数值优化求解以验证上述算法的有效性。为方便算法实施,采用Yalmip建模工具箱[19]进行优化问题建模,利用轻量级凸优化求解算法包ECOS[20]进行SOCP问题求解。所有优化算法运行的计算机配置为: CPUi7-4790@3.6GHz, 8G内存。
表1给出了CAV任务描述,给出了任务起点和目标点的水平位置、高度,并给出了禁飞区的中心点坐标以及半径。优化过程中禁飞区次序未知,但根据算法流程步骤2中的逐点检测可以方便地施加禁飞区约束。第一个禁飞区的半径远小于CAV的转弯能力,第二个禁飞区半径则足够大。

表1 CAV任务描述

式(35)中的迭代收敛停止条件设置为δ=0.03,离散化区间Δτ=1/300,即N=300。
为对比说明本文所提方法的有效性,将序列凸优化求解结果(记为SOCP)与伪谱法求解结果(记做GPOPS)进行了对比,其中伪谱法求解主要基于开源Matlab工具箱GPOPS[21]进行。
数值求解过程中,序列凸优化SOCP经过7次迭代获得最优解,整个优化计算的CPU时间为8.918s,而GPOPS优化则需要21.109s;SOCP和GPOPS求得的最优飞行时间分别是2869.2s和3061.7s,显然,序列凸优化方法无论是效率还是性能上都要明显优于GPOPS。两种方法的优化结果如图2~图6所示。
图2为地面航迹,可以看出SOCP解和GPOPS解都满足两个禁飞区约束,但SOCP的轨迹更逼近禁飞区的边界。图3是高度曲线和速度曲线,两种方法的解均严格满足终端高度和速度约束,其中SOCP解的高度曲线变化更加平滑。两种优化方法得到的弹道倾角和航向角曲线变化趋势与幅度(如图4所示)基本保持一致,弹道倾角变化较小,航向角平滑。图5给出泛化升力系数和倾侧角曲线,整个过程均满足控制变量约束条件,但GPOPS得到的控制量抖动幅度较大,而SOCP由于引入新的控制变量进行松弛处理,抖动幅度较小。图6给出了两种方法得到的热流、动压以及过载曲线,从图中可以看出,尽管SOCP方法中过载曲线末端较大,但所有约束在整个过程中均满足给定条件。
4 结论
具有热流、动压、过载以及禁飞区约束的再入轨迹优化问题是一个强约束的非线性动态规划问题,本文通过引入归一化时间和辅助控制变量,结合轨迹线性化和无损凸化处理技术,将原问题转化为标准的SOCP问题,利用开源凸优化求解器ECOS求解,快速获得最优轨迹。归一化时间尽管增加了控制变量,但有效避免了终端时间自由所带来的离散化问题,同时也避免了以能量为自变量时无法从起始点进行离散化的缺陷。辅助控制变量的引入则在一定程度上避免了序列优化过程中容易引起的控制量高频振荡的不利因素,提高了优化解的工程适用性。数值优化结果以及对比实验结果表明,本文所提方法是一种行之有效的再入轨迹快速优化方法,计算效率和性能均优于传统的非线性规划方法。
[1] Lu P. Entry guidance: a unified method[J]. Journal of Guidance Control and Dynamics, 2014, 37(3):713-729.
[2] Jorris T R, Cobb R G.Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J]. Journal of Guidance Control and Dynamics, 2009, 32(2): 551-572.
[3] Rao A V. A survey of numerical methods for optimal control[J].Advances in the Astronautical Sciences, 2010, 135(1): 1-32.
[4] Poustini M J, Esmaelzadeh R, Adami A. A new approach to trajectory optimization based on direct transcription and differential flatness[J]. Acta Astronautica, 2015,107:1-13.
[5] Petropoulos A E, Sims J A. A review of some exact solutions to the planar equations of motion of a thrusting spacecraft[C]. NASA Jet Propolsion Laboratory Technical Reports,USA,2002.
[6] Betts J T. Very low-thrust trajectory optimization using a direct SQP method[J].Journal of Computational and Applied Mathematics, 2000, 120:27-40.
[7] Williams P.Hermite-Legendre-Gauss-Lobatto direct transcription in trajectory optimization[J]. Journal of Guidance Control and Dynamics,2009, 32(4): 1392-1395.
[8] Zhao J, Zhou R, Jin X. Reentry trajectory optimization based on a multistage pseudospectral method[J]. Scientific World Journal, 2014, 2014:1-13.
[9] Garg D, Patterson M, Darby C, et al. Direct trajectory optimization and costate estimation of general optimal control problems using a Radau pseudospectral method[J]. Computational Optimization and Applications,2011, 49(2):335-358.
[10] Chai D, Fang Y W,Wu Y L,et al. Boost-skipping trajectory optimization for air-breathing hypersonic missile[D]. Astronautical Science and Technology, 2007.
[11] Huntington G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[J]. Massachusetts Institute of Technology,2007.
[12] Andersen E D, Roos C, Terlaky T. On implementing a primal-dual interior-point method for conic quadratic optimization[J]. Mathematical Programming, 2003, 95(2): 249-277.
[13] Blackmore L,Acikmese B,Scharf D P .Minimum-landing-error powered-descent guidance for Mars landing using convex optimization[J]. Journal of Guidance Control, and Dynamics, 2010, 33(4): 1161-1171.
[16] Liu X F, Lu P. Solving nonconvex optimal control problems by convex optimization[J]. Journal of Guidance Control and Dynamics, 2014, 37(3): 750-765.
[17] Liu X F, Shen Z J,Lu P. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance Control and Dynamics (Articles in Advance),2015,39(2): 1-15.
[18] Jorris T R. Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[D]. Doctor, Engineering and Management, Air University, Ohio, US, 2007.
[19] Löfberg J.YALMIP : a toolbox for modeling and optimization in MATLAB2004[C]. Proceedings of the CACSD Conference, Taipei, Taiwan, 2004.
[20] Domahidi A, Chu E, Boyd S.ECOS: an SOCP solver for embedded systems[C].European Control Conference, Zurich, Switzerland, 2013.
[21] Garg D, Hager W W,Rao A V .Pseudospectral methods for solving infinite-horizon optimal control problems[J]. Automatica,2011,47: 829-837.
Rapid Planning of Reentry Trajectory viaSequential Convex Optimization
ZHAO Dang-Jun,LIANG Bu-Ge,YANG De-Gui,SHI Wei
(School of Aeronautics and Astronautics, Central South University, Changsha 410083, China)
A sequential convex optimization scheme is proposed for rapid solving the reentry trajectory optimization problem constrained by heat flux, dynamic pressure, normal load, and multiple no-fly zones. The normalized time is used as the independent variable to accommodate the problem of free terminal time, and auxiliary control variables are introduced to alleviate the high frequent chatter in the sequential convex optimization solution. Further, the linearization, discretization, and convexification techniques are used to convert the original concave and nonlinear optimization problem into a standard second order conic programming problem, which can be rapid solved by convex algorithms. Numerical results and comparison study reveal that the proposed method is efficient and effective to solve the problem of reentry trajectory optimization with multiple constraints, and the computational efficiency and performance of the proposed method is superior to that of the classical nonlinear programming.
Sequential convex optimization; Reentry trajectory optimization; Lossless convexification; Second order conic programming
2017-03-20;
2017-04-13基金项目:湖南省自然科学基金(14JJ3024)
赵党军(1978-),男,博士,副教授,主要从事飞行器制导与控制研究。E-mail:zhao_dj@esu.edu.cn
V411
A
2096-4080(2017)01-0034-07

