换种教学方式让 学生走出学习困境
王利芬
摘要:教学《角的度量》这节课时,教师总结出的“二合一看”量角要诀仍然解决不了学生“量角器不知如何摆放”“内外圈度数读错”等问题。此时应尝试换位思考,真正从学生的角度去寻找学生量角出错的原因,教师变身为引导者帮助学生走出学习困境。
关键词:小学数学;角的度量;错误原因;策略
中图分类号:G623.5 文献标识码:B 文章编号:1009-010X(2017)16-0024-04
《角的度量》是一节经典的操作技能课。教学这节课时,教师总是会煞费苦心总结出“二合一看”的量角要诀,可这简洁又颇得要领的要诀却仍然解决不了学生“量角器不知如何摆放”“内外圈度数读错”的问题。笔者认为,“二合一看”的量角要诀,其实是成人的偏好,学生以形象思维为主,老师抽象概括出的词语反而会增加学习的难度。我们要学会换位思考,把自己“变成小孩子”,真正从学生的角度去寻找学生量角出错的原因,并探索出相应的化解策略,换种学习方式,帮助学生走出学习困境。
一、已有的度量经验产生的负迁移
学生在学习角的度量之前,其实已经有相关的度量经验,如长度、面积的度量。测量长度、面积时“度量单位累加”的经验与测量角度本质上是一致的。但由于度量对象的特征不同,学生测量长度的经验又会对测量角度带来负面影响。例如,学生测量长度时是从尺子的0刻度线开始量的,强调的是测量物体与0刻度线对齐;而量角则从量角器的中心点开始,让角的顶点与中心点重合。这与学生原有的测量经验不同。学生受测量“从头”开始量的经验影响,在量角时则会出现将角的顶点与量角器半圆的“尖”重合的错误。
化解策略:挖掘有效的度量经验,找准学生自研量角的生长点
片段一:
(一)回顾已有度量经验
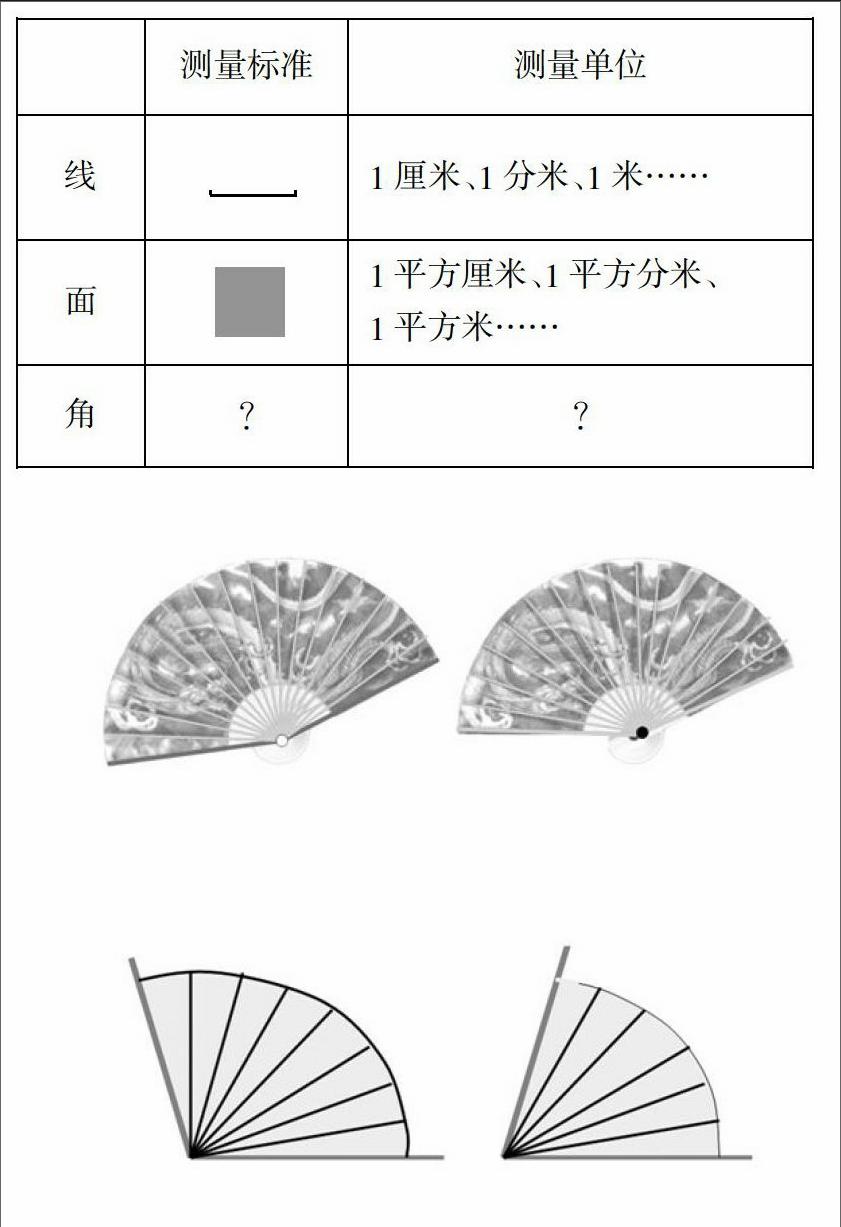
师:要想测量一个长方形每条边的長度,你会选择哪个长度单位?要测量它的面积,又会选择哪个面积单位?
师:长方形中也有角,要想测量这个角的大小,你又会用哪个单位呢?
生:我猜也是用一个小角来量的。
根据学生的回答,教师填表。
(二)自研“以角量角”
师:要比较这两把扇子上角的大小,怎么比?
生1:重叠
生2:我有个更好的办法,扇子上的折痕是一些小角,可以数一数里面的小角。
师:是呀,数小角不仅能比较出角的大小,还能知道大了多少,这个办法的确很好。(出示∠1和∠2)你还能精确比较出这两个角的大小吗?
生:能,只要有一个小角,在里面摆小角就可以。
(教师给学生提供一些小角,学生通过小组合作完成两个角的大小比较。如上图)
生:角1比角2大了2个小角。
教育家陶行知曾说“我们要以自己的经验做根,以这经验发生的知识做枝,然后别人的知识才能接得上去,别人的知识方才成为我们知识的一部分。”学生在学习“角的度量”之前已经“储备”过相关的度量经验,教师要合理选择,巧用正迁移,避免负向迁移。此环节,教师巧妙地帮助学生回顾已有的测量经验,用一小段线段单位量线段,一块面积单位量面积,引发学生类比的思维,启发学生对角的度量的猜想:角是不是也以一个小角来量角?接着教师以“比较两把扇子上角的大小”再次激活学生已有的关于量角方法的经验——重叠法。正是教师对学生已有经验的有效挖掘,找准学生新知识的生长点,学生才在交流、讨论、与操作中自发地探究出了“用小角比角”这个度量角的新方法。不仅积累了量角的经验,还为后面介绍量角器做了铺垫。
二、量角器的构造复杂,理解难度大
量角器的结构与直尺不一样。量角器呈半圆形,在课前访谈中我们发现,量角器半圆形的轮廓使相当一部分学生错误而又坚定地认为:量角器不能量角——因为量角器上有曲线,曲线不能量直线。量角器的本质是单位小角的集合,但由于量角的基本单位1。的角太小,在量角器上难以完整反映,量角器上1。的分割线去掉了大部分,只在圆周上留下一些刻度;为了使用的方便,量角器还设计了内外两圈刻度。面对如此繁多的数据,学生无所适从。再加之学生所使用的量角器“千奇百怪”,尤其是中部镂空的量角器,很难在其上准确找到“角”。
化解策略:精设助学单,驱动学生在互助互研中解读量角器的构造价值。
片段二
(一)小组互助完成助学单
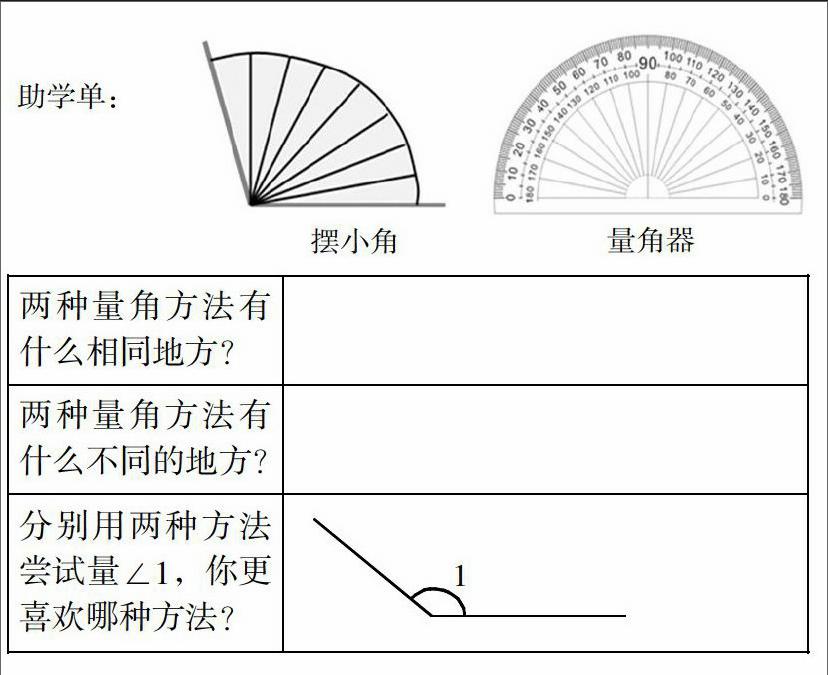
组织学生在阅读课本的基础上小组合作完成助学单:
提醒:遇到同题司以查阅数学书
(二)汇报问题一:找小角
生:我们组发现他们都有小角。都是把小角拼在了一起。
师:你在量角器上找到哪些小角?它的顶点在哪?边在哪?
学生纷纷指出各种小角。
生:我发现这些小角的顶点都是同一个,在直边的中间。
师:这个共同的顶点就叫做量角器的“中心点。”
(三)汇报问题二:认刻度
生:我们组发现量角器上有两圈数字。但我们不明白是什么意思?
生:刻度是告诉我们角的度数,刻度标着几,就是几度。
生:每一条线都标着2个刻度,到底看哪个度数呢?
生:如果角是从左边一圈的0度开始数,就看外面的,如果从右边一圈的0度开始数就看里面的度数。
师:你们能找出10°、30°、31°角吗?(生找角,并汇报)
师:量角器上没有31°,你怎么找到31°角的?
生:每一个大格被平均分成10份,所以一份就代表1°。
师:你们能指指1°角吗?感觉怎样?
生:1°角很小。
师:为什么量角器不把1°角的线画出来?
(课件同时出示:没有省略1°分割线的密密麻麻量角器和省略了1°分割线的普通量角器)endprint
生:把所有1°角标出来,太麻烦!直尺上的刻度也是这样,没有全部标。
生:如果全部标上,我们数角的度数,密密麻麻看不清楚。
(四)汇报问题三:比优劣
生:我们组喜欢量角器,摆那么多个小角很麻烦,量角器更方便。
生:如果用摆小角的方法,最后量出来是14个小角多一点。而用量角器量是145度,更精确一点。
弗雷登塔尔说“泄露一个可以由学生自己发现的秘密,那是‘坏的教学法,甚至是罪恶的”。如果学生伸手或跳一跳能摘到桃子,教师绝不要代劳。而“认识量角器”就是学生能自己摘到的桃子,教师只需要给他们提供一份精致的助学单,学生就会以助学单为跳板,自发地运用类比方法去探究、去发现、去解读量角器量角的本质与价值。整个探究过程,始终是学生通过自己阅读教材、自主尝试、小组交流讨论和全班释疑来解决学习过程中产生的错误和遇到的困难。事实证明,没有了教师手把手地教,学生不仅能摘到“桃子”,而且摘得又多又好。
三、无法还原角的形成过程
学生在测量角的度数时,只将被测量的角看作是静止的图形而非动态的过程——将角的两边孤立地量,就像量线段那样,认为只要把一条边对准尺子的起点,另一条边指着几就读几。而量角器有2圈刻度,2条0刻度线,量角时,则要思考量角器的度数与角以哪条边为起点边打开的关系,否则就会出现读错内外圈度数的错误。其实,不论是何种开口方向的角,如果都能还原成以其中任一条边作为起点,慢慢打开,而度数随之增加的动态过程,那么,度量时内外圈刻度读错的问题自当迎刃而解。
化解策略:以动制静,点拨学生把复杂问题简单化、本质化
片段三:
还原角的动态展开过程
师:屏幕上的这个角,你能想象出它在量角器上是怎样展开的吗?
生:可以看成是从右边往左边慢慢张开。也就是把右面的边视为0刻度线慢慢展开。
生:也可以看成是从左边往右边慢慢打开,把左面的边视为0刻度线慢慢展开。
按照学生所答,课件演示将角移至量角器上,让其中一边分别与左右两边的0刻度线重合,并出现一支笔,让笔尖顺着数据增加的方向慢慢移动,边移动边显示出1°、2°、5°、10°、20°……数度数,直到接近角的另一条边,将度数准确读出。
师:通过刚才的量角,你发现量角的时候要特别注意什么?
生:一定要从0刻度线开始顺着数下去。
生:其实我从量角器上任何一个度数开始数也是可以的。就像刚才60°的角,我将一条边对齐90°再往左数,数到150°的位置,就是150°减90°等于60°了。
师:刚才这种新方法好不好?
生:虽然可以算出度数,但还是很麻烦,因为要通过计算才能得出角的度数。
生:我觉得有道理,只是他将90°的边当成了0刻度线。
师:是的,这正是量角的关键,选准了起始边,确定了张开的方向,读出度数就是件容易的事了。
课件继续演示量角器上角慢慢张开至60°、90°、120°的过程。
师:比较60°与120度角张开的大小与他们的度数,你发现了什么?
生:角的一条边张开没有超过90度的中线,是个锐角,就读锐角的度数,超过90°的中线是个钝角就读钝角度数,
大数学家华罗庚说过“量起源于量,数起源于数”。此环节,教师首先引导学生将一个个静态的角由小到大在一个动态的过程中产生,引领学生在1°、2°、3°、5°、10°、20°、30°、40°……这样数的过程中确定角的度数。学生在按照开口方向数度数的过程中,只需数出一个角里面包含有几个1°角,就能确定角的度数,不用思考0刻度线在左还是在右,也不管是内圈刻度还是外圈刻度。这其实是在把复杂问题简单化、本质化,学生既免去了记住那些琐碎、复杂的量角步骤,又掌握了量角方法,并且再次感悟了量角的本质,可谓一举多得。接着,教师又调动起学生关于直角、锐角、钝角的表象,为学生树立90°直角的标杆,学生可借此标杆快速数出角的度数。这样的教学由于符合了学生的认知规律,学生学起来自然轻松、清楚。
总之,在教学“角的度量”这类操作技能课时,教师不仅需要做课堂的“掌舵者”,掌控学习方向,更需要做课堂的“隐身人”,把学生推向课前,让学生“先试后讲”,在思考、交流、傾听、争论和发现中自主学习。“自习”“自得”的知识、技能,学生的理解必然更加深刻,学生的困惑才能迎刃而解。
【责任编辑 王悦】endprint
教育实践与研究·小学版2017年6期
