全面“二胎”新政策下我国人口增长率及经济发展关联性研究
夏伟宇,朱家明
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
全面“二胎”新政策下我国人口增长率及经济发展关联性研究
夏伟宇,朱家明
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
本文以中国的人口为研究对象,预测未来2016-2020年的人口数.本文首先对数据进行预处理,其次对模型进行识别和定阶,然后再对模型作参数估计并进行诊断和检验,最后做出预测并基于预测结果对人口政策提出相应的建议.
EVIEWS;预测模型;经济发展;时间序列
1 引言
多年来计划生育这一基本国策的实施对我国的人口问题及发展问题产生的积极作用不可忽视.然而随着社会和经济的发展,我国人口面临着新的问题,如劳动力短缺、养老金困局、人口老龄化、男女性别比失调等等,一方面,这要求我们需要放开计划生育的约束;而另一方面,人口增长过快,会造成交通堵塞、就业困难、饥饿贫困、资源缺乏、环境拥挤等问题.本文以我国人口为研究对象,通过对2016-2020年人口数量的预测来分析上述问题.本文研究的目标是建立一个比较系统、有一定创新性和借鉴性的人口预测方法及其模式,提供一个人口预测的参考案例.
2 新政策实施后对未来人口的预测
2.1 模型简介
ARIMA模型,全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA),其中ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归,p为自回归项;MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数.所谓ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型.ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程.
2.2 建模步骤
ARIMA模型预测的基本程序:
2.2.1 数据预处理
根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律,对序列的平稳性进行识别.一般情况下,如果一个时间序列是平稳的,则自相关函数成指数衰减或正弦衰减,且衰减的很快,如果是非平稳的,则衰减很慢.也可以用单位根检验,判断其平稳性,对非平稳序列可以采用差分变换和对数变换对数据进行平稳化和均质化处理.
2.2.2 模型的识别与定阶
根据时间序列模型的识别规则,建立相应的模型.若平稳序列的偏相关函数是截尾的,而自相关函数是拖尾的,可断定序列适合AR模型;若平稳序列的偏相关函数是拖尾的,而自相关函数是截尾的,则可断定序列适合MA模型;若平稳序列的偏相关函数和自相关函数均是拖尾的,则序列适合ARMA模型.(截尾是指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质(比如AR的PACF);拖尾是ACF或PACF并不在某阶后均为0的性质(比如AR的ACF).
2.2.3 参数估计
进行参数估计,检验是否具有统计意义.对AR模型的参数采用最小二乘法估计,MA和ARMA模型采用迭代式的非线性最小二乘法进行估计.
2.2.4 假设检验
进行假设检验,诊断残差序列是否为白噪声,如果残差序列不能近似为一个白噪声序列,则需要再次对模型进行识别.
2.2.5 预测分析
利用已通过检验的模型进行预测分析,并与预留的实际值进行比较,得到相对误差,从而进一步判断所拟合的模型的精度.
2.3 实证分析
2.3.1 数据的收集
本文选取了1986-2015年三十年间中国人口数据[1].如表1所示.
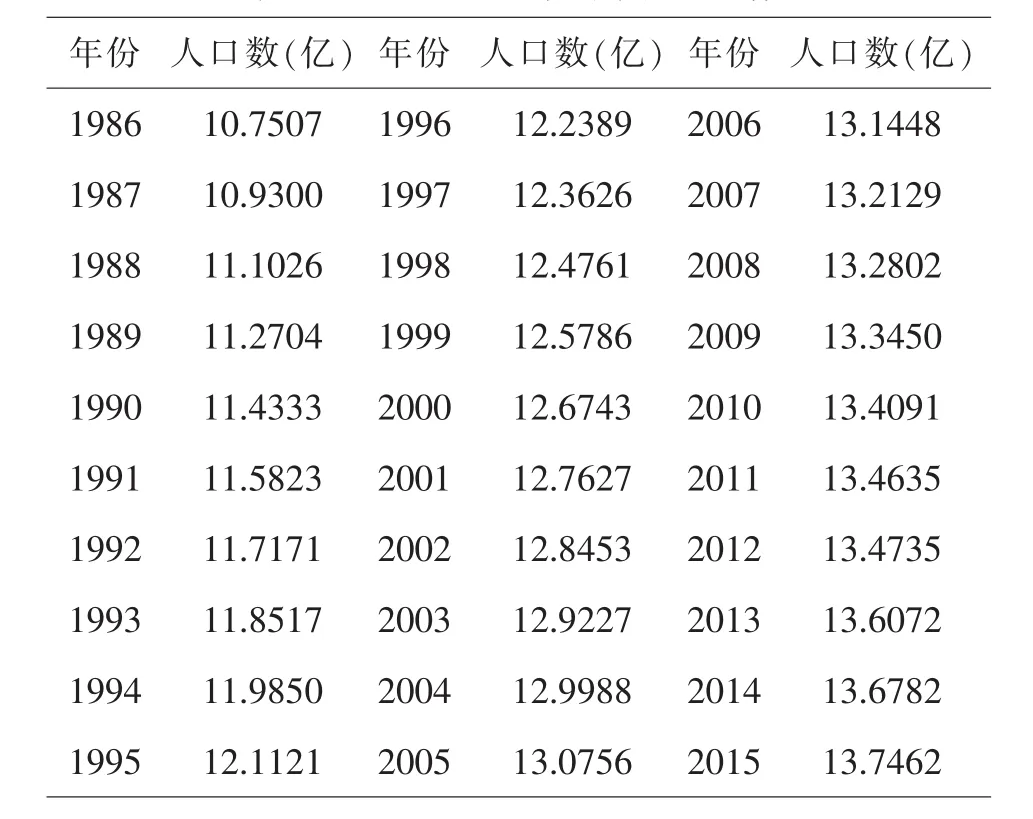
表1 1986-2015年间中国人口数
2.3.2 数据的预处理
本文使用1986-2013年的人口数据为样本,利用ARIMA模型预测未来十年的人口数,其中,2014与2015年的人口数是模型检验数据,用于和预测值进行比较,评价预测的精度.首先做出1986-2013年的中国人口时序图,将该序列命名为X,如图1所示.
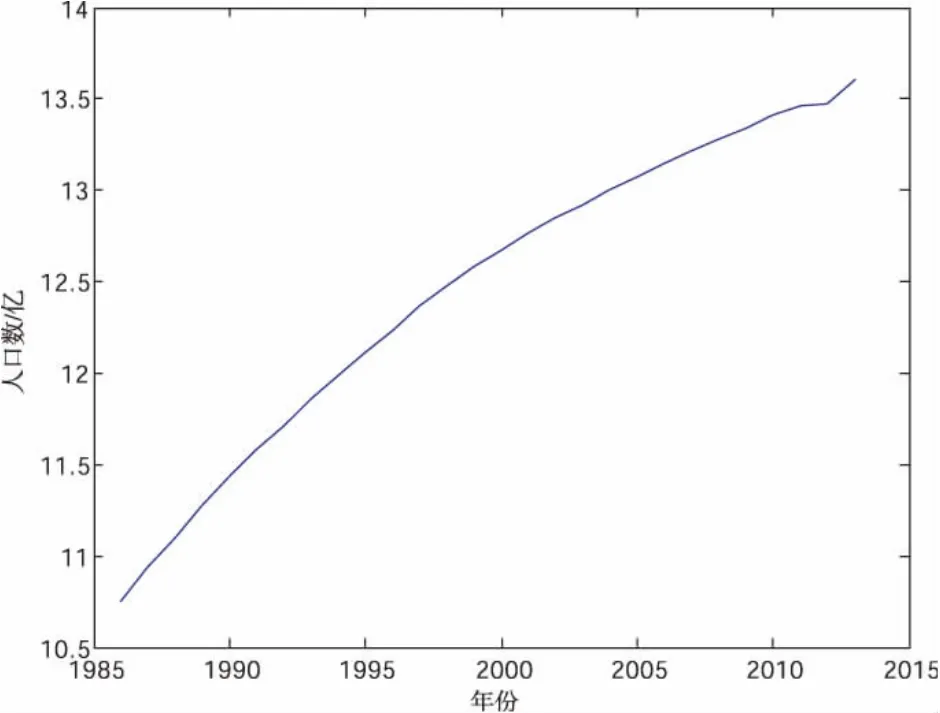
图1 1986-2013年中国人口数时序图
由时序图可以明显看出,1986-2013年中国人口呈上升趋势,因此可以初步判断该序列不平稳、方差也不平稳,因此,对该组序列作对数变换,并用Eviews做出时序图和单位根检验,如图2、3所示.
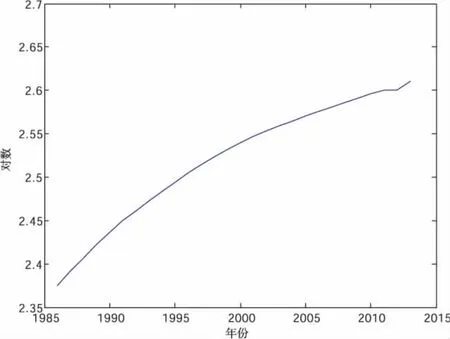
图2 1986-2013年中国人口对数的时序图
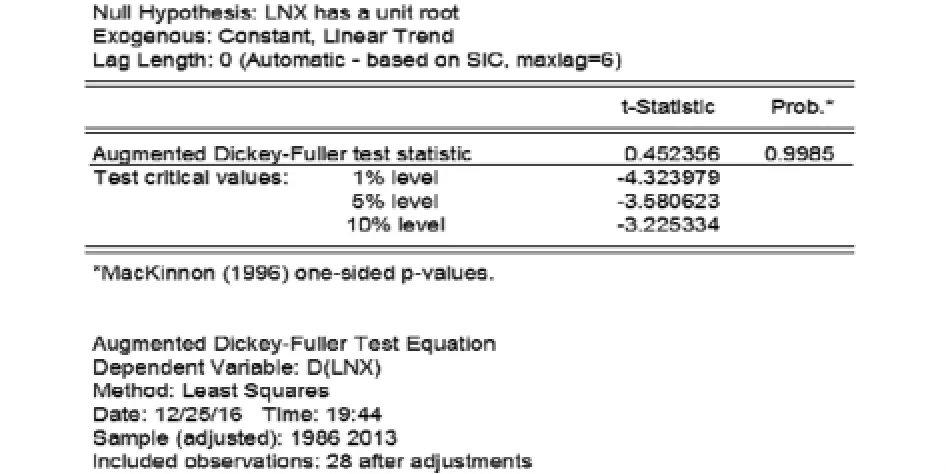
图3 单位根检验
由图2可知,中国人口的对数序列也具有明显的上升趋势,因此,该序列依旧不平稳,对该序列进行单位根检验可以发现,序列在1%、5%、10%的显著性水平下,ADF检验值为0.452356,均大于在1%、5%、10%的显著性水平下的临界值,且P值远远大于0.05并接近于1,同样也说明了序列不平稳.因此,在建立模型前,需要对模型进行平稳化处理,由于一阶差分可以消除线性趋势,二阶差分可以消除二次曲线趋势,因此,我们对序列进行二次差分,得到时序图如图4.

图4 二阶差分时序图
由图4可知,经过对原始序列的取对数、二阶差分,原始序列的趋势性已基本消除,序列呈现出较小的波动性并趋于平稳,为了进一步确定序列的平稳性,需要对其进行单位根(ADF)检验,如图5所示.
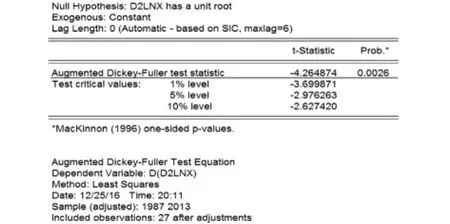
图5 单位根检验
由图5可知,序列在1%、5%、10%的显著性水平下,ADF检验值为-4.264874,均小于各显著性水平下的临界值,因此序列为平稳时间序列,能够用序列来拟合模型.
2.3.3 模型的识别与定阶
序列滞后18阶的自相关与偏自相关图如图6所示.
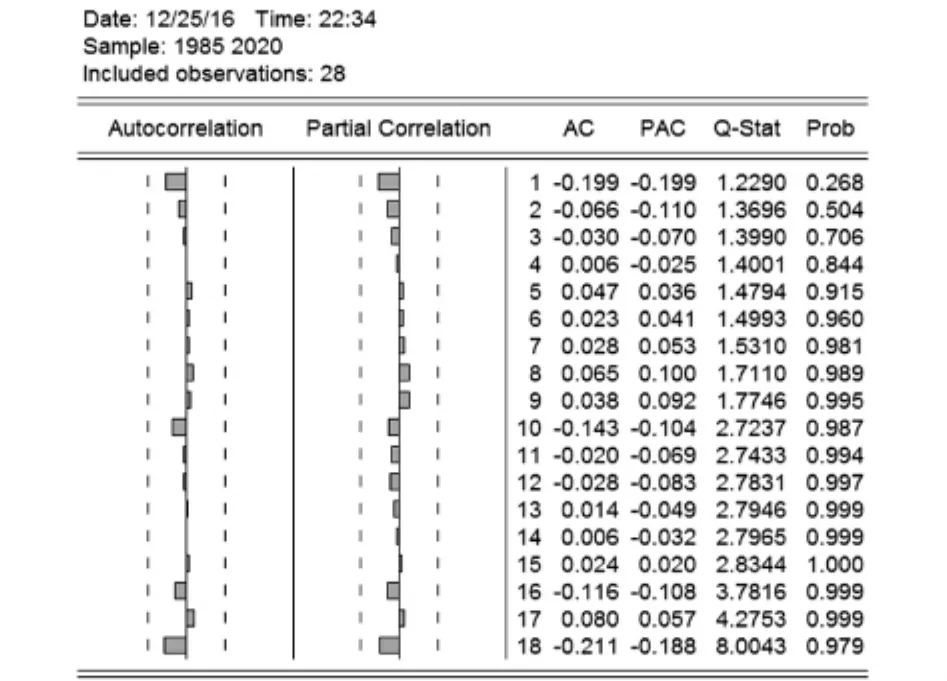
图6 自相关与偏自相关图
由图6可知,二阶差分后的序列自相关函数和偏自相关函数均呈现拖尾性,因此可以建立ARMA模型,二阶差分后的自相关函数从第2阶开始下降很大,数值不太显著,因此我们设定滑动平均系数q=2.二阶差分后的偏自相关函数也从第2阶开始下降很大,因此确定自回归系数p=2,初步建立ARIMA(2,2,2)模型.
2.3.4 模型的估计与检验
运用最小二乘估计,对序列进行ARIMA(2,2,2)拟合估计.结果如图7所示.
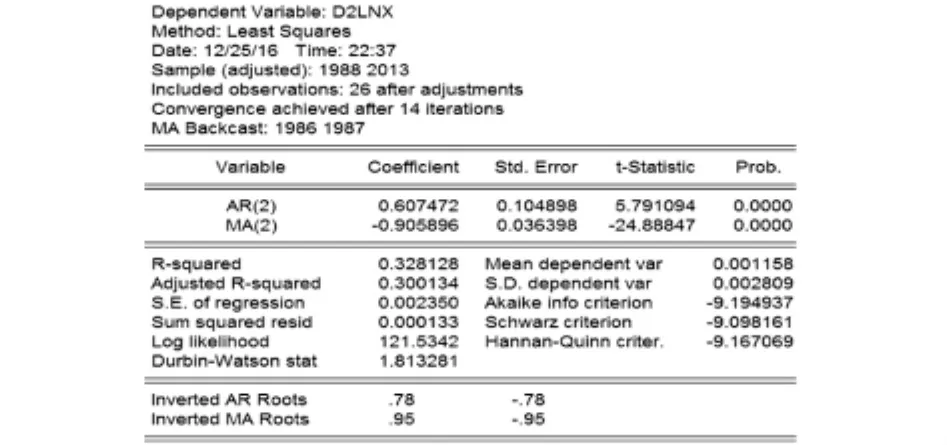
图7 ARIMA(2,2,2)拟合估计
由图7可知,拟合出的模型为疏系数模型.疏系数ARIMA(2,2,2)模型中的P值为0,因此,模型显著,认为疏系数ARIMA(2,2,2)能较好地拟合该序列.
紧接着对残差序列进行白噪声检验,根据模型ARIMA(2,2,2)对序列进行回归拟合,如图8所示.

图8 模型拟合折线图
从图8可以得到,途中的实际值和拟合值基本一致,残差序列类似于白噪声,较平稳,没有明显的趋势性,模型拟合效果较好.对残差作自相关和偏自相关图分析,如图9所示.
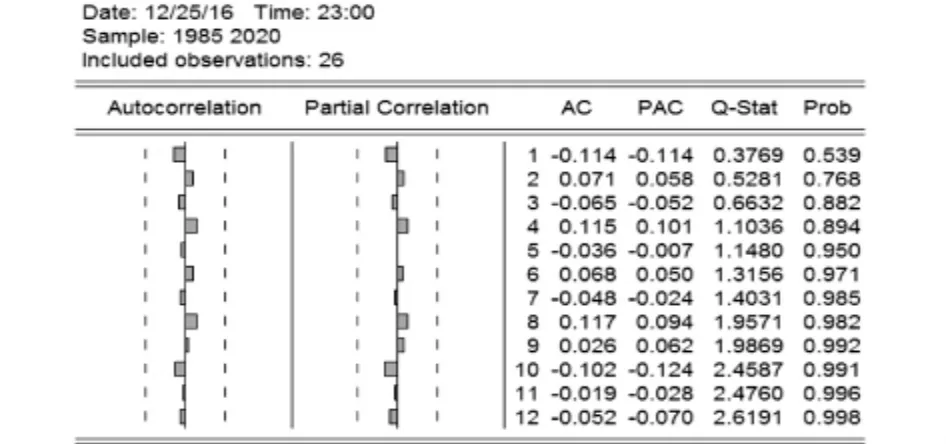
图9 残差序列的自相关和偏自相关图
由图9可知,模型的残差不存在相关序列,为进一步对模型进行检验,做出残差的单位根检验图.如图10所示.
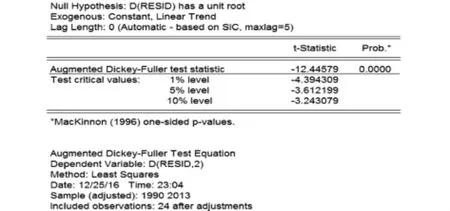
图10 残差的单位根检验图
由图10可知,序列在1%、5%、10%的显著性水平下,ADF检验值为-12.44579,均小于各显著性水平下的临界值,因此序列为平稳时间序列.
因此,最终选定ARIMA(2,2,2)模型对序列进行描述.
2.3.5 模型的预测
运用EVIEWS对拟合模型后的序列进行预测,预测从1985-2020年中国人口数,动态预测图如图11所示,静态预测图如图12所示[2].
图中实线代表的是XF的预测值,两条虚线则提供了2倍标准差的置信区间[3].实际值处于2倍标准差之内,图的右侧给的是评价预测的一些标准.由图12的预测评价标准中,可以看到,Theil不相等系数为0.002232,非常小,综合其他标准,可以得出,静态预测较动态预测效果良好[4].通过静态预测,将2014-2015年的中国人口数真实值与预测值进行比较,求出预测误差,如表2所示[5].
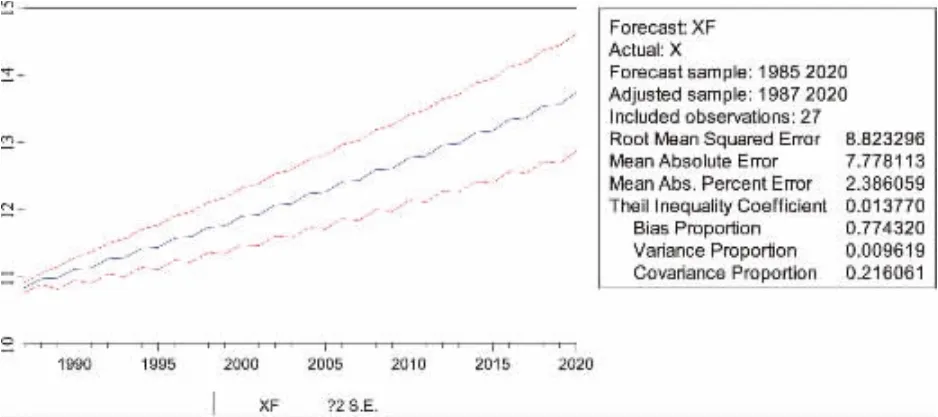
图11 模型的动态预测图
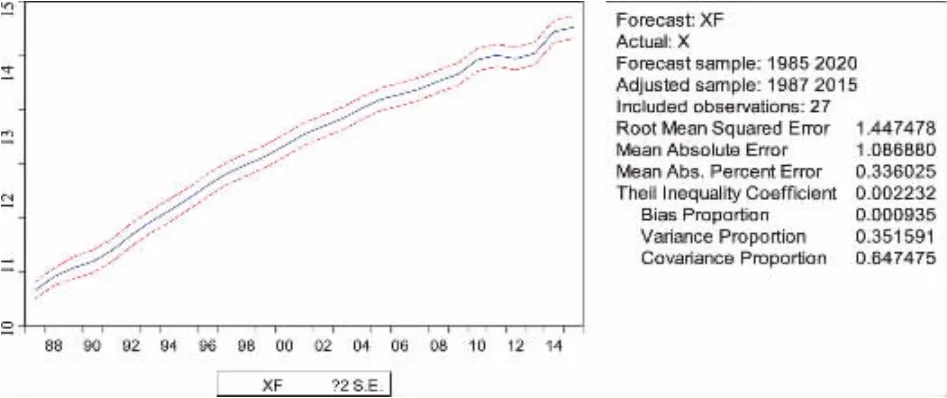
图12 模型的静态预测图
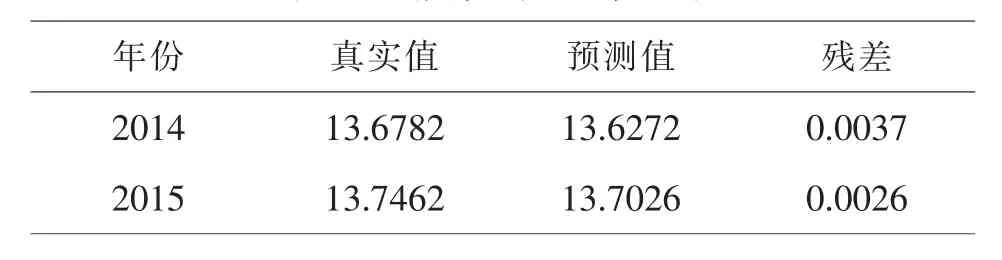
表2 真实值与预测值比较
由表2可知,残差小于0.05,预测值和实际值非常接近,模型用于短期预测效果是好的.通过动态预测对2016-2020年年底中国人口数预测,可得到图13[6].

图13 2016-2020年年底中国人口数预测(亿)
将预测值列入表中,见表3.
从预测结果可以看出,未来五年内中国人口仍将呈上升趋势.因此,实行二胎政策将促进我国经济的发展.
3 结束语

表3 2016-2020年年底中国人口预测值
通过对中国人口这一组真实数据进行时间序列分析,可得出以下结论:
3.1 运用ARIMA模型进行建模和预测,分析结果说明,用ARIMA模型对中国总人口进行建模预测是可行且可靠的,预测结果表明中国人口数在短期内仍将呈上升趋势,因此有必要采取必要的政治及经济措施来进行调控,对人口的控制起到指导作用.
3.2 在运用ARIMA模型对中国总人口预测分析的过程中,我们发现该模型对于短期预测较合理,但对于长期预测存在一定缺陷.该模型的短期预测准确度很高,预测结果的稳定性好,对数据的预测有一定的价值,是一种很好的预测短期总人口量的方法.
3.3 对中国总人口拟合的ARIMA(2,2,2)模型本身比较简单,对原始数据的要求较少,易于分析和应用.
3.4 通过对中国人口的预测可以得到对未来中国人口结构和经济发展改善的有益启示,为改善人口结构提出新的思路,并为我国将来的人口控制提供新的手段[7].
〔1〕中华人民共和国统计局.http://www.stats.gov. cn/.
〔2〕夏伟宇,朱家明,闫业铃,张海珍,陈益杨.基于新政策对芜湖人口发展的计量分析[J].贵阳学院学报(自然科学版),2017(01):72-76+85.
〔3〕李浩,杨辉.农业循环经济效率评价问题研究——基于黑龙江省2005—2012年农业经济发展数据的解析[J].黑龙江畜牧兽医,2016,(08):29-32.
〔4〕陈盼,陆卫群.ARIMA模型在区域人口预测的应用分析[J].当代经济,2016(06):111-113.
〔5〕李宝洪.循环农业经济体系的含义和建立[J].中国农业信息,2015(18):24-25.
〔6〕韩绍庭,周雨欣.多元线性回归与ARIMA在中国人口预测中的比较研究[J].中国管理信息化, 2014(22):100-103.
〔7〕人口和计划生育工作情况的总结.http://www. 5ykj.com/Article/zjbgnzzj/36942.htm.2016-12-26.
C921;O224
A
1673-260X(2017)08-0003-04
2017-06-04
国家自然科学基金(11601001);安徽财经大学国家级大学生创新创业训练计划(201610378056)

