晚自习期间学校教室资源优化配置——以宿州学院为例

杨星星

（宿州学院 数学与统计学院，安徽 宿州 234000）

晚自习期间学校教室资源优化配置
——以宿州学院为例

杨星星

（宿州学院 数学与统计学院，安徽 宿州 234000）

晚自习期间，教室资源的合理配置方案不仅可以为学生提供良好的学习环境，而且还可以为学校节约很大的一笔电力资源的支出.本文通过问卷调查估计每天上晚自习的学生人数和到每个自习区的概率以及学生对教室环境的满意度.分区考虑教室用电量和学生满意度建立0-1整数规划模型求解最优教室配置方案并应用Lingo软件对所建立最小化线性规划模型进行求解.所得的优化方案合理，结果较为可信.

教室资源优化配置；线性规划模型；Lingo软件

在大学校园里，你会发现这样一个现象：教室里空无一人，但灯是全开着的.不少大学的用电浪费可谓严重，集中体现在晚自习用电上.地球上的资源是有限的，人类的快速发展已经给环境带来严重的破坏，人与自然的矛盾愈演愈烈.拥有智慧和科技的现代人有责任也有能力做到资源节约，环境保护.资源节约并不是一个浩瀚工程，可以来自我们身边，来自我们的举手投足间.但是，仅仅靠人们的自觉性来节约资源是不够的.本文从运筹学和统计学的角度，通过建立数学模型来优化晚自习期间教室资源配置从而达到节约用电的目的.

1 问题分析

本文是针对宿州学院的自习教室提出的资源优化，自然要结合本校实际.首先，影响晚自习期间的用电量与开放的教室数量有着直接的关系.怎样做到恰好满足学生需求是解决优化配置问题的关键.教室的配置是一个滞后的行为，它依赖于学生对教室的需求量，而这样的需求量决定于上晚自习的人数，所以对上晚自习人数的预测显得非常重要.在预测了每天上晚自习人数和在保证最大满意度的情况下，合理配置教室资源.这样不仅有效的杜绝了一人一室或是无人一室的现象，还提高了晚自习教室的利用率从而达到电力资源的节约.

根据宿州学院实际情况，我校的教室分为四个区，分别是：教学楼、工科楼、逸夫楼和实验楼.而对于不同的专业选择自习的区域也是不同的，大部分的人都倾向于选择自己熟悉的环境进行学习.所以我们不能笼统的把这四个区统一到一起，然后笼统的进行教室配置，那样得到的配置方案是缺乏人文主义的.我们必须根据实际情况将晚自习的区域进行划分，在各区域内部进行优化配置达到部分用电最省进而使得整体优化达到整体用电最省.

2 基本假设

（1）全校学生上晚自习是相互独立的事件

（2）如果一个教室被使用，则教室里的灯全开

（3）假设所有的学生在选择教室时都趋于人少的地方

（4）学生到各个自习区上自习的概率是不变的

（5）每天上晚自习的概率不随时间而改变

（6）晚自习时间为T=3小时

（7）学生并不在意教室在几楼

（8）无论什么样的教室分配方案，管理人员都能接受

3 建立规划模型

我们所考虑的问题是通过预测上晚自习学生的人数，以学生人数、学生满意度和教室数量来控制和优化教室资源配置，达到用电最省.所以我们研究的是一类最小化的规划问题.目标函数是“用电量函数”，约束条件是“学生人数”，“教室数量”，“学生满意度”.

3.1 目标函数的确定

其中Zj为第j个自习区的用电量；Rji表示第j个自习区的编号为i的教室开放状况，我们设为虚你变量[3]：

Mji表示第j个自习区的编号为i的教室的灯管数目，Wji表示第j个自习区的编号为i的教室的灯管的功率，T开灯时间.

3.2 约束条件的确定

对于一个教室，校方希望充分利用.但实际上，学生往往会选择人数较少的教室自习，所以才造成少数人占用了多数的资源.本次规划实质上是在一定程度上极大地控制学生对教室资源的选择.

所以有以下约束条件：

其中mtj是时间t第j个自习区的学生人数，Sji表示第j个自习区第i个教室的座位数，t=1,2,3,4,5,6,7.

3.3 估计上自习学生人数

经调查，我校全日制在校学生有15000人，而对于大四的学生我们不予考虑，因为他们上晚自习的比率较小，不考虑他们有利于模型的简化同时又不会给结果造成损失.所以我们研究的学生人数限定在8000人.

通过问卷调查获得如下各表数据：

表1 学生到各自习区上晚自习的概率

P(L)：表示学生上自习的总概率；P(J)：表示到主教学楼上自习的概率；P(G)：表示到工科楼上自习的概率；P(Y)：表示到逸夫楼上自习的概率；P(S)：表示到实验楼上自习的概率.

表2 每天上自习的概率

M：星期一；T：星期二；W：星期三；TH：星期四；F：星期五；ST：星期六；SU：星期日.

令：

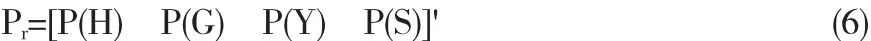
则：各教室人数为：

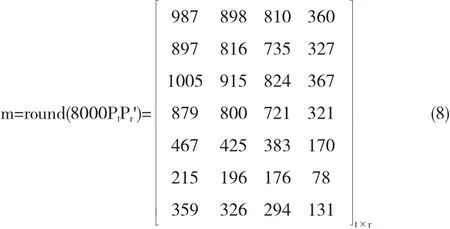
4 模型求解

建立了上述目标函数和约束条件很容易用交互式线性规划软件lingo11.0求解.经实地调查我校我的自习区教室情况如表3、4、5、6.

表3 自习区1—主教学楼教室情况调查

表4 自习区2—工科楼教室情况调查

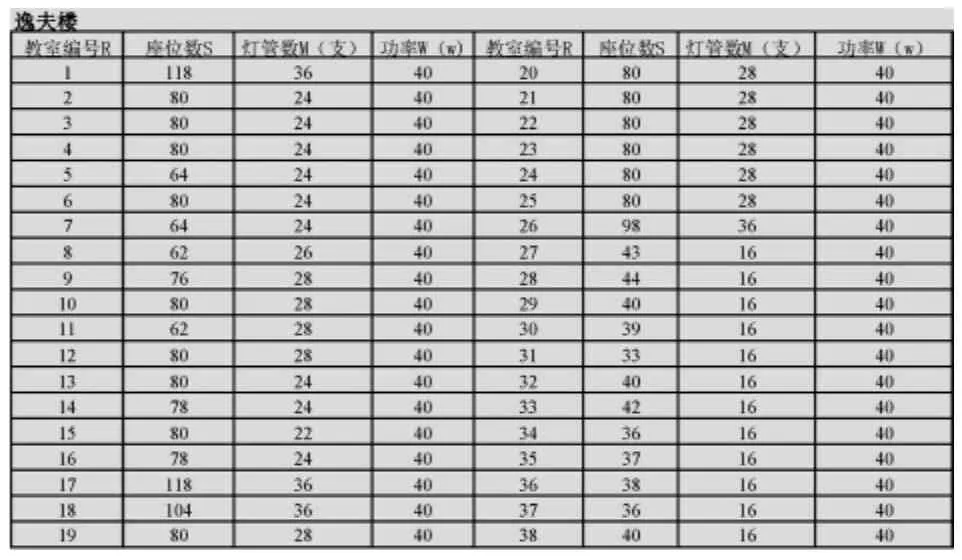
表5 自习区3—逸夫楼教室情况调查

表6 自习区4—实验楼教室情况调查

4.1 自习1区—教学楼的模型求解

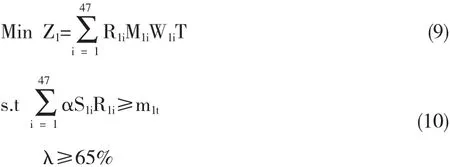
Lingo程序[4]如下：

sets:

jiaoshi/1..47/:S,R,M,W;!S:教室的座位数；R：教室的使用情况（1为使用，0为不使用）；

M:为教室的灯管数；

W为每个灯管的功率;

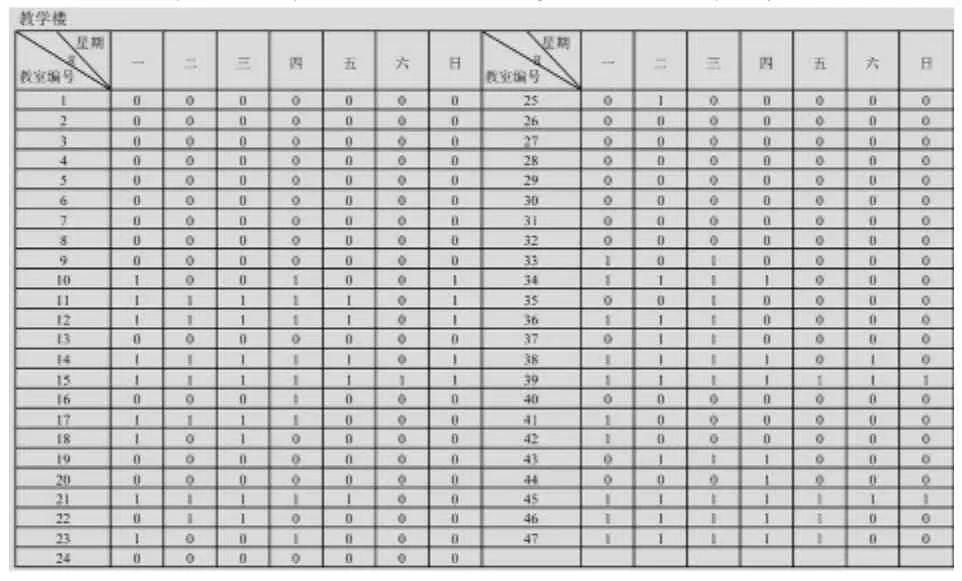
表7 自习1区—教学楼教室配置方案

4.2 自习2区—工科楼的模型求解

同上利用lingo软件求得教室开放方案整理如下：

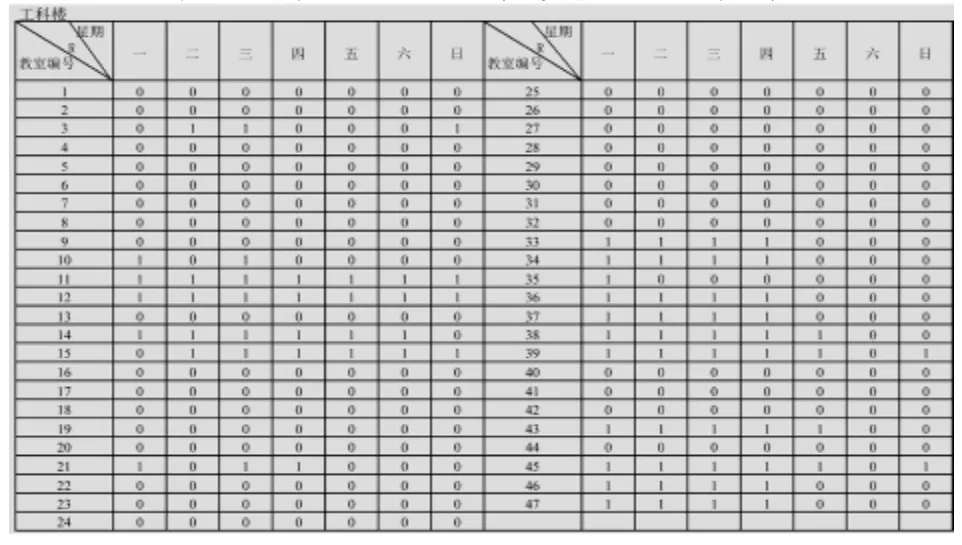
表8 自习2区—工科楼教室配置方案

4.3 自习3区—逸夫楼的模型求解

同上利用lingo软件求得教室开放方案整理如下：

表9 自习3区—逸夫楼教室配置方案

4.4 自习4区—实验楼的模型求解

同上利用lingo软件求得教室开放方案整理如下：

表10 自习4区—实验楼教室配置方案

4.5 最优用电量

对四个自习区的优化模型求解可得局部最有用电量为：

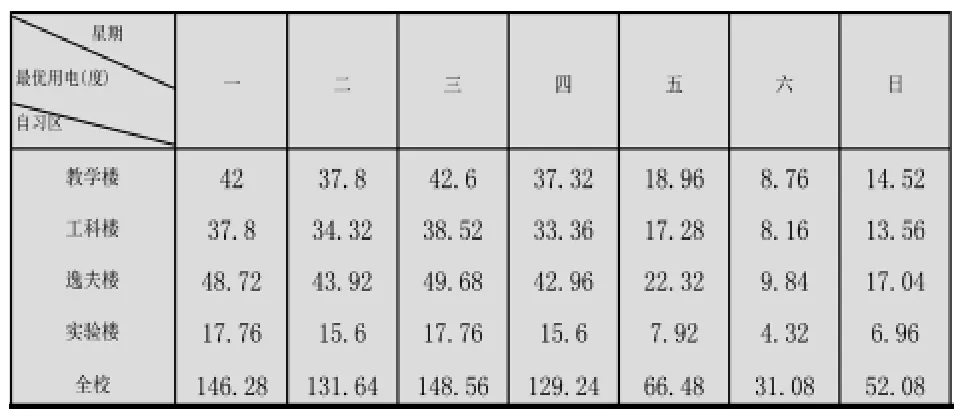
表11 各自习区及全校的最优用电量

由上表可知各个自习区每天最优用电量以及全校最优用电量，上述模型实现了由局部最优达到整体最优的目的：星期一我校晚自习期间优化后耗电量为146.28度，星期二耗电131.64度，星期三耗电148.56度，星期四耗电129.24度，星期五耗电为66.48度，星期六耗电为31.08度，星期日耗电为52.08度.

〔1〕S.P.勃雷达兰等，著，翟立林等译.应用数学规划[M].北京：机械工业出版社，1983.(Stephen P.Bradley,Arnoldo C.Hax,Thomas L.Magnanti, Applied Mathematical Programming,Addison-Wesley Publ.Co.,1977.)

〔2〕朱求长.运筹学及其应用[M].武汉：武汉大学出版社.

〔3〕庞皓.计量经济学[M].北京：科学出版社，2010.

〔4〕谢金星.优化建模与LINDOLINGO软件[M].北京：清华大学出版社，2005.

〔5〕林纯.某高校教室资源紧缺状况分析与应对[J].福建工程学院学报，2012(04).

〔6〕顾兴强,蔡小飞.高校教室资源优化配置研究[J].四川教育学院学报，2009(09).

〔7〕高友智,费佳,祝丹.关于高校教室资源管理的研究[J].中国电力教育，2007(09).

〔8〕任条娟,刘斌,孙惠荣.高校教室资源管理的问题与改革思路——以浙江树人大学为例[J].浙江树人大学学报(人文社会科学版)，2008(06).

O224

A

1673-260X（2017）08-0007-04

2017-05-05

宿州学院2015质量工程项目（201510379083）