筒体直径对旋风分离器性能的影响
袁 怡, 孙国刚, 周发戚, 孙占朋
(中国石油大学 化学工程学院 过程流体过滤与分离北京市重点实验室, 北京 102249)
筒体直径对旋风分离器性能的影响
袁 怡, 孙国刚, 周发戚, 孙占朋
(中国石油大学 化学工程学院 过程流体过滤与分离北京市重点实验室, 北京 102249)
筒体直径是影响旋风分离器效率和压降的重要结构参数。以硅微粉为原料,在保证几何结构相似的基础上,对筒体直径分别为200、300、400 mm的Stairmand型旋风分离器进行冷态对比实验,考察了不同情形下筒径对旋风分离器分离性能的影响。结果表明,旋风分离器按几何相似放大,筒径增大,在同一入口气速下,分离效率下降而压降升高;在同一处理气量下,分离效率和压降都下降。如将入口尺寸与处理气量固定,其它尺寸按几何相似放大,筒径增大则旋风分离器的分离效率增加、压降降低。进而又用几个较新的分离模型对实验进行了计算比较,发现模型计算结果与实验结果的趋势大体一致,基本上能预测筒径变化对旋风分离器分离效率与压降的影响趋势,但都不能定量计算筒径对其分离性能的影响。
旋风分离器;筒体直径;效率;压降;模型计算
旋风分离器是气-固分离过程中一种常用的设备,因其结构简单,无运转部件,适用于高温高压等条件,目前在石油、化工、冶金、能源、环境等诸多领域得到广泛应用。要将在小模型实验研究中开发出的高效旋风分离器应用到工业中去,必须经过放大设计和工业设计,但小型实验设计经过放大后其性能如何变化,迄今并无成熟的计算方法[1]。在保证几何相似的基础上,对旋风分离器尺寸放大可通过增大筒体直径来实现。一般认为:随着筒体直径的增大,旋风分离器的分离效率降低,压降升高[2]。然而,筒体直径对旋风分离器性能的影响取决于多种因素。
金有海等[3]对蜗壳式旋风分离器进行相似放大的试验研究,认为筒体直径越小,离心力场越强,从而粒子被分离的效率越高。Jin等[4]采用CFD数值模拟的方法,发现当质量流率和入口截面一定,增大筒体直径,旋风分离器的总分离效率提高,压降几乎不变,流场更稳定。袁惠新等[5]、方麒先[6]认为在入口速度一定的条件下,旋风分离器的压降随着筒径的增大而增大。刘书贤等[7]对催化裂化装置沉降器粗旋在尺寸放大后的压降进行数值模拟研究,认为尺寸放大后粗旋的压降减小。宋健斐等[8]对旋风分离器直径尺寸变化时的气相流场进行数值模拟研究,认为随着筒体直径的增大,流场流态保持相似性。迄今为止,前人虽然做了不少关于筒径对旋风分离器性能影响的研究工作,但大多集中于采用数值模拟的研究手段,且其得出的结论并不全面,很难对工程实践形成有效指导。因此,寻找筒体直径对旋风分离器性能的影响规律,就成为迫切需要解决的课题。
在本研究中,以Stairmand型旋风分离器[9]为基准模型,选择结构参数和入口气速作为变量,分别以理论模型计算及实验测量的手段考察旋风分离器几何放大后性能的变化规律,以期获得更为全面的认识,从而为旋风分离器的优化设计及工业应用提供有益参考。
1 试验装置与方法
采用Stairmand型旋风分离器为基准模型,筒径(D)分别为200 mm、300 mm、400 mm,下接料腿(L)为1500 mm,用有机玻璃制造,试验所用旋风分离器尺寸结构如图1所示。图1(a)中入口截面系数KA是1个与筒径及入口高宽有关的无量纲数[10],KA=7.85,各部分尺寸随筒径等比例变化;图1(b)中入口高×宽为144 mm×58 mm,排气管插入深度为144 mm,其他各部分尺寸随筒径等比例变化。
实验介质为常温空气,粉料为硅微粉,颗粒密度约为2600 kg/m3,采用BT-9300S 型激光粒度分布仪进行粒度分析,中位粒径为10.94 μm,粒径分布dp如图2所示。试验在吸风负压状态下操作,试验流程如图3所示,入口气速由标准毕托管测量;风量通过阀门调节;粉料从分离器入口处的加料斗人工加料,加料质量浓度为10 g/m3,通过加料时间来控制加料浓度;分离器压降用U型管测量,分离效率采用加料、收料称重法计算。分离器入口段有一定长度,使粉料和气体在分离器入口段充分混合,混合后的携尘气体经过旋风分离器的分离后由排气管排出到风机外排系统。

图1 旋风分离器结构尺寸Fig.1 Critical dimensions of cyclone separator(a) Stairmand cyclone separator with inlet cross-section coefficient KA=7.85;(b) Stairmand cyclone separator with inlet size 144 mm×58 mm
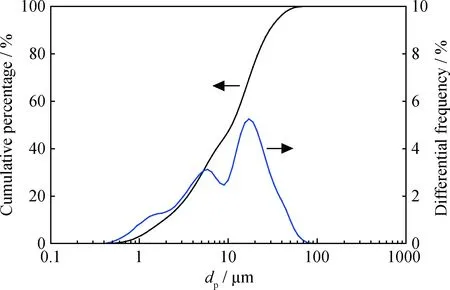
图2 实验用硅微粉粒径分布Fig.2 Experimental silica powder size distribution
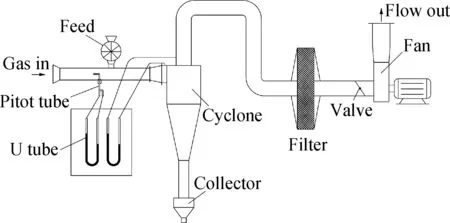
图3 实验装置示意图Fig.3 Schematic drawing of the experimental setup
2 试验结果及分析
2.1 筒体直径对旋风分离器效率的影响
采用图1(a)Stairmand型分离器,入口截面系数相同(KA=7.85),筒体直径D分别为200、300、400 mm。(1)选取10、15、20、25 m/s 4个气速,由试验得到该组旋风分离器在不同气速下的分离效率如图4所示。从图4可以看出,入口气速相同,筒径等几何尺寸等比例放大,旋风分离器分离效率降低;还可以发现,随着入口速度的增加,旋风分离器效率会出现转折点,存在1个最大效率速度,且筒径的变化对该最大效率入口速度的大小几乎没有影响。这是因为入口气速增大,离心力场增强,效率增加;当气速增大到一定值后,湍流及颗粒碰撞弹跳等导致沉积在器壁处的一些颗粒重新被卷扬起来,加上灰斗夹带增多等不利因素的综合影响,导致旋风分离器效率有所降低。(2)选取处理气量0.167 m3/s,由试验得到此时该组旋风分离器在不同筒径下的效率如图5所示。从图5可以看出,同一入口气量时,几何尺寸按同一比例放大,随着筒径增大,入口截面尺寸增大,入口气速下降,旋风分离器内离心力场减弱,从而导致分离器的分离效率降低。
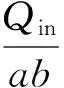
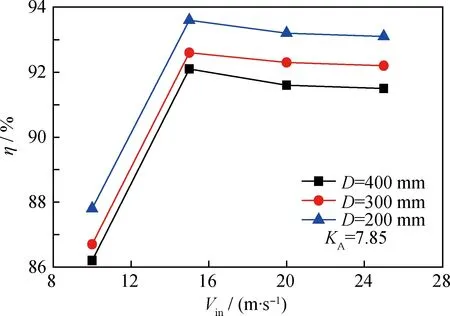
图4 分离效率(η)-入口气速(Vin)曲线(KA=7.85)Fig.4 Efficiency(η)-gas velocity(Vin) curve (KA=7.85)

图5 不同筒径(D)下的旋风分离器分离效率(η)Fig.5 The efficiency(η) of cyclone under varied cylinder diameters(D)
2.2 筒体直径对旋风分离器压降的影响
筒体直径对旋风分离器压降的影响如图6所示。从图6可以看出,当旋风分离器几何尺寸按比例放大,同一入口气速下,随着筒体直径的增加压降增大;同一处理气量下,随着筒体直径的增加压降降低;当固定入口截面尺寸大小,旋风分离器其他尺寸按比例放大,则入口气速及处理气量均相同,旋风分离器的压降随着筒径的增大而减小。

图6 不同筒径(D)下旋风分离器的总压降(Δp)Fig.6 The pressure drop(Δp) of the cyclone under varied cylinder diameters(D) (a) The same inlet velocity; (b) The same consumption flow
3 模型预测结果与分析
3.1 旋风分离器分离模型的预测结果分析
作为旋风分离器分离效率的预测模型即分离模型,从20世纪50年代以后在国内外取得广泛的研究。各研究者基于不同假设,从不同的角度阐述了各自理论,归纳起来主要有“平衡轨道”模型、“停留时间”模型以及介于两者间的混合模型。表1列出了几种近年来较具代表性的旋风分离器分离模型具体效率计算方法。

表1 旋风分离器分离效率的计算模型Table 1 Calculation model of separation efficiency for cyclones
笔者以实验测量的方法对不同筒径下的Stairmand型旋风分离器的分离效率进行了研究,分离模型也可以预测分离器的效率。在工业过程中,总分离效率通常是1个最常用的评价指标,将表1中模型预测的切割粒径或粒级效率换算成总效率,总效率是通过这样方式计算的:首先按照颗粒粒径分布划分为N个粒度级的质量组分,每个质量组分之和构成了全部颗粒质量;然后,用每个质量分数乘以该组分平均粒径下的粒级效率,所以N个粒度级组分的总和就得到总效率。数学表达式为:
(1)
式中,ηi为第i个组分的粒级效率,wi为第i个组分的质量分数。
图7为旋风分离器总效率的实验值与模型计算值对比。图7(a)、(b)分别为入口气速15 m/s及20 m/s 下,几何尺寸相似放大的旋风分离器分离效率随筒径的变化关系;图7(c)为同一处理气量下,几何尺寸相似放大的旋风分离器分离效率随筒径的变化关系;图7(d)同一处理气量下,保持入口截面尺寸大小不变,其它尺寸相似放大的旋风分离器分离效率随筒径的变化关系。将不同模型计算结果与实验结果对比,可以看出模型预测结果和实验结果随筒径变化的趋势大体上一致,但二者之间还存在一定的差距。这是因为旋风分离器内部三维强旋湍流运动的复杂性,各理论模型均为研究者们基于各自的假设,通过对其工作过程的简化而得,虽具有一定的准确性,但与实际分离过程相比,仍存在一定的局限性。

图7 旋风分离器总效率(η)的试验值与模型计算值对比Fig.7 Comparison of overall efficiency(η) between experiments and model prediction(a) Overall efficiency with inlet violet 15 m/s (KA=7.85); (b) Overall efficiency with inlet violet 20 m/s (KA=7.85);(c) Overall efficiency with consumption flow 0.167 m3/s(KA=7.85);(d) Overall efficiency with consumption flow 0.167 m3/s (a×b=144×58 mm2)
3.2 旋风分离器压降模型的预测结果分析
目前的旋风分离器压降计算公式很多是经验关联式,且多用阻力系数ξ来表达。表2列出了几种旋风分离器阻力系数的具体计算方法。
在本研究中,选择了7个经验模型来预测旋风分离器的压力损失,图8为本实验条件下不同筒体直径的旋风分离器实验压降结果与模型压降计算值的对比。从图8(a)中可知,当KA=7.85且入口气速相同时,袁怡等[21]模型计算值与试验值有相同的变化趋势且偏差较小,其余模型均忽视了筒径对旋风分离器压降的影响,总是保持一定值;从图8(b)中可知,当KA=7.85且处理气量相同时,各个模型计算值与试验值随筒径变化的趋势一致,即随着筒体直径的增加,旋风分离器压降降低;从图8(c)中可知,当入口高宽保持一定值时,除Barth等[18]模型外,其余模型预测结果与实验结果变化趋势一致,即随着筒体直径的增加,旋风分离器压降降低。

表2 旋风分离器阻力系数的计算模型Table 2 Calculation model of pressure drop coefficient for cyclones
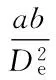
4 结 论
以Stairmand型旋风分离器为基准模型,通过实验测量和理论模型计算研究了筒体直径对旋风分离器性能的影响。
(1)分离器结构尺寸按几何相似放大,入口气速相同时,随着筒体直径的增大分离效率降低,压降升高;处理气量一定时,随着筒体直径的增大分离效率降低,压降降低。
(2)固定入口截面尺寸,其它结构尺寸按几何相似放大,即处理气量及入口气速都相同时,随着筒体直径的增大分离效率升高,旋风分离器压降降低。
(3)模型计算与实验值对比发现,近年文献中的几个较新的分离模型基本上能够预测旋风分离器分离效率和压降随筒径的变化趋势,但模型预测值都和实验结果有一定差距。
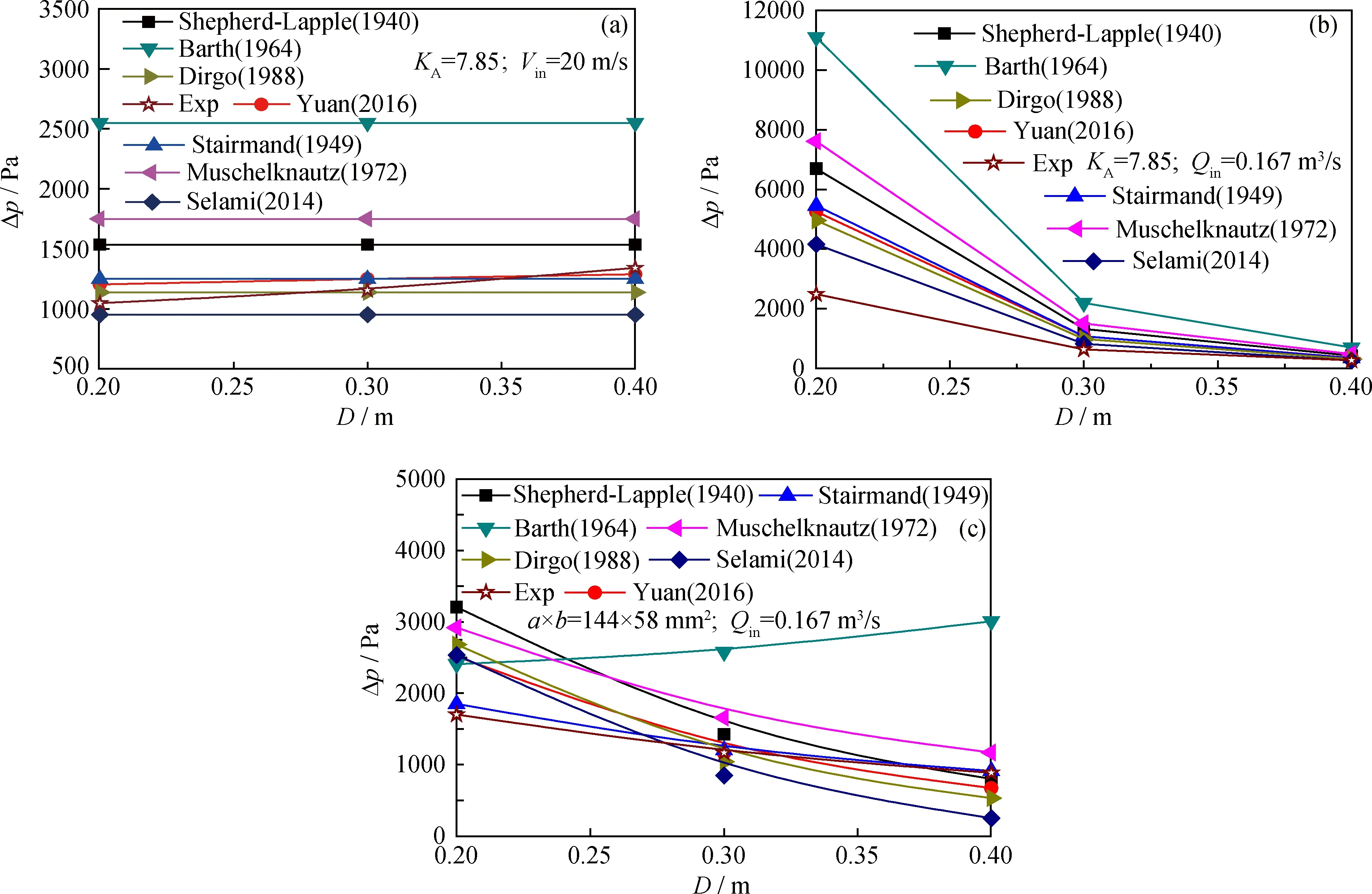
图8 旋风分离器压降(Δp)的试验值与模型计算值对比Fig.8 Comparison of pressure drop(Δp) between experimental value and model prediction(a) Pressure drop with inlet violet 20 m/s (KA=7.85); (b) Pressure drop with consumption flow 0.167 m3/s (KA=7.85);(c) Pressure drop with consumption flow 0.167 m3/s (a×b=144×58 mm2)
符号说明:
a——矩形入口高度,m;
ad——入口宽度修正系数;
a0r——平均流量宽度,m;
b——矩形入口宽度,m;
B——排尘口直径,m;
Cc——坎宁修正系数;
CD——曳力系数;
Cin——入口浓度,kg/m3;
D——分离器筒体直径,m;
De——排气管直径,m;
dp——颗粒直径,m;

Ds——摩擦面的无量纲平均直径;
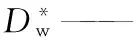
d50——切割粒径,m;
D0——筒径修正系数,D0=0.3 m;
f——含尘气流与壁面摩擦系数;
f0——纯净气流与壁面摩擦系数;
Fs——旋风分离器器壁的总面积,m2;
g——重力加速度,m/s2;
h——旋风分离器筒体高度,m;
hc——旋风分离器锥体高度,m;
H——旋风分离器总高度,m;
KA——入口截面系数,KA=πD2/4ab;
Ks——绝对粗糙度,m;
LVS——自然旋风长,m;
n——旋流的旋涡指数;
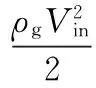
Qin——入口气体流量,m3/s;
R——分离器筒体半径,m;
Re——排气管半径,m;
Rin——入口半径,m;
Re——气体雷诺数;
r0r——颗粒轨迹的平均半径,m;
Rw——分离器筒体半径,m;
rt——内外旋流分界半径,m;

S——排气管插入深度,m;
tres——总气体停留时间,s;

Uθw——分离器器壁颗粒切向速度分量,m/s;
Ve——排气管平均轴向气速,m/s;
Vin——入口气体速度,m/s;
V0——入口平均速度,m/s;
Vθe——排气管壁面气体切向速度,m/s;
Vθw——分离器器壁气体切向速度,m/s;
wi——第i个组分的质量分数
希腊字母:
ηi——粒级效率;
η——总分离效率;
φ——惯性碰撞系数;
ζ——进口损失;
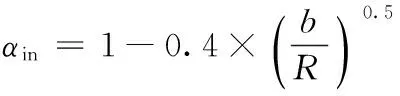
ζe——器内旋流损失;
ρg——气体密度,kg/m3;
ρp——颗粒密度,kg/m3;
ρstr——灰带密度,kg/m3;
δ——颗粒轨道半径与出口半径之比;
v——气体运动黏度,m2/s;
μg——气体动力黏度,Pa·s;
ξ——纯气流阻力系数;
ξst——纯气流阻力系数(Stairmand模型)。
[1] 时铭显, 吴小林. 旋风分离器的大型冷模试验研究[J].化工机械, 1993, 20(4): 188-189. (SHI Mingxian, WU Xiaolin. Experimental study on large-scale cold mold cyclone[J].Chemical Machinery, 1993, 20(4): 188-189.)
[2] 金国淼. 除尘设备[M].北京: 化学工业出版社, 2002: 40-41.
[3] 金有海, 时铭显. 旋风分离器相似放大实验研究[J].石油大学学报, 1990, 14(5): 46-55. (JIN Youhai, SHI Mingxian. Experimental studies on scale-up of separator cyclone[J].Journal of the University of Petroleum, China, 1990, 14(5): 46-55.)
[4] JIN W L, YANG H J, DONG Y L. Effect of the cylinder shape of a long-coned cyclone on the stable flow-field establishment[J].Powder Technology, 2006, 165(1): 30-38.
[5] 袁惠新, 李丽丽. 物性和结构参数对旋风分离器压降影响的数值模拟[J].矿山机械, 2010, 5(38): 91-94. (YUAN Huixin, LI Lili. Numerical simulation of material properties and structural parameters’ effects on pressure drop of the cyclone separator[J].Mining Machinery, 2010, 5(38): 91-94.)
[6] 方麒先. 旋风分离器结构尺寸对压降影响的实验研究[D].北京: 中国石油大学(北京), 2015.
[7] 刘书贤, 孙国刚, 时铭显. 催化裂化装置沉降器粗旋结构设计探讨[J].炼油技术与工程, 2008, 10(38): 25-30. (LIU Shuxian, SUN Guogang, SHI Mingxian. Structure design of a rough-cut cyclone in fluidized catalytic cracking disengager[J].Petroleum Refinery Engineering, 2008, 10(38): 25-30.)
[8] 宋健斐, 杨光福, 陈建义, 等. 旋风分离器内气相流场的相似模化分析(Ⅱ)尺寸参数[J].化工学报, 2010, 9(9): 2274-2279. (SONG Jianfei, YANG Guangfu, CHEN Jianyi, et al. Similarity analysis of modeling of gas phase flow field in cyclone separator(Ⅱ) Size parameters[J].CIESC Journal, 2010, 9(9): 2274-2279.)
[9] OSCAR L, SGROTT J, DIRCEU N, et al. Cyclone optimization by COMPLEX method and CFD simulation[J].Powder Technology, 2015, 277(1): 11-21.
[10] YANG J X, SUN G G, GAO C Z. Effect of the inlet dimensions on the maximum-efficiency cyclone height[J].Separation and Purification Technology, 2013, 105(1): 15-23.
[11] ZHANG R, BASU P. A simple model for prediction of solid collection efficiency of a gas-solid separator[J].Powder Technology, 2004, 147(1): 86-93.
[12] 钱付平, 张吉光, 杨丰, 等. 静电旋风分离器结构尺寸的优化设计[J].锅炉技术, 2004, 35(2): 10-13. (QIAN Fuping, ZHANG Jiguang, YANG Feng, et al. Optimization design of configuration size on electro cyclone[J].Boiler Technology, 2004, 35(2): 10-13.)
[13] ZHAO B T. Prediction of gas-particle separation efficiency for cyclones: A time-of-flight model[J].Separation and Purification Technology. 2012, 85(2): 171-177.
[14] AVCI A, KARAGOZ I. Effects of flow and geometrical parameters on the collection efficiency in cyclone separators[J].Journal of Aerosol Science, 2003, 34(7): 937-955.
[15] SHEPHERD C B, LAPPLE C E. Flow pattern and pressure drop in cyclone dust collectors cyclone without intel vane[J].Industrial & Engineering Chemistry, 1940, 32(9): 1246-1248.
[16] DIRGO J. Relationships between cyclone dimensions and performance[D].Boston: Univ of Havarad, 1988.
[17] 陈建义. 切流返转式旋风分离器分离理论和优化设计方法的研究[D].北京: 中国石油大学(北京), 2007.
[18] BARTH W, LEINEWEBER L. Beurteilung und auslegung von zyklonabscheidern[J].Staub, 1964, 24(2): 41-55.
[19] MUSCHELKNAUTZ E. Die berechnung von zyklonabscheidern für gase[J].Chemie Ingenieur Technik, 1972, 44(1-2): 63-71.
[20] DEMIR S. A practical model for estimating pressure drop in cyclone separators: An experimental study[J].Powder Technology, 2014, 268: 329-338.
[21] 袁怡, 孙国刚, 周发戚. 旋风分离器的压力降计算[J].炼油技术与工程, 2016, 46(10): 39-44. (YUAN Yi, SUN Guogang, ZHOU Faqi. Pressure drop calculation of cyclone separator[J].Petroleum Refinery Engineering, 2016, 46(10): 39-44.)
Effects of the Cylinder Diameter on Cyclone Performance
YUAN Yi, SUN Guogang, ZHOU Faqi, SUN Zhanpeng
(BeijingKeyLaboratoryofProcessFluidFiltrationandSeparation,CollegeofChemicalEngineering,ChinaUniversityofPetroleum,Beijing102249,China)
Cylinder diameter was an important structural parameter of the cyclone. In this paper, a series of laboratory cyclone model experiments were carried out to investigate the effect of the cylinder diameter on Stairmand cyclone performances.The cylinder diameter was 200 mm, 300 mm and 400 mm, and the powder was microsilica. The results showed that, according to the geometric similarity to enlarge cyclone, if the inlet velocity was the same, with the increase of the cylinder diameters, the collection efficiency of the cyclone decreased and the pressure drop increased. Moreover, if gas flow rate was the same, with the increase of the cylinder diameters, the collection efficiency of the cyclone decreased and the pressure drop decreased. As the inlet size was fixed, if enlarging other dimensions with geometric similarity, namely inlet velocity and gas flow rate remained unchanged, with the increase of the cylinder diameters, the collection efficiency of the cyclone increased and the pressure drop decreased. In addition, under the experimental conditions, the comparison between the computations of several recent performance prediction models and the experimental date, showed that the theoretical models could predict the tendency of cylinder diameter effects on cyclone performances.
cyclone; cylinder diameter; collection efficiency; pressure drop; model calculations
2016-08-02
国家自然科学基金(21276274)和国家重点基础研究发展计划“973”项目(2014CB744304)资助
袁怡,女,硕士,从事气-固分离的数值模拟及实验研究;Tel:010-89734820;E-mail:m15201106422@163.com
孙国刚,男,教授,博士,从事气-固分离及流态化工程研究;Tel:010-89734820;E-mail:ggsunbj@163.com
1001-8719(2017)04-0738-08
TQ021.1
A
10.3969/j.issn.1001-8719.2017.04.019

