基于改进人工蜂群算法的概率积分法参数反演

刘 奇，朱建军，苏军明,2，何永红,3，孙明星

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083;2.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;3.湖南科技学院 土木与环境工程学院,湖南 永州 425199)

基于改进人工蜂群算法的概率积分法参数反演

刘 奇1，朱建军1，苏军明1,2，何永红1,3，孙明星1

(1.中南大学 地球科学与信息物理学院，湖南 长沙 410083;2.中国电建集团中南勘测设计研究院有限公司,湖南 长沙 410014;3.湖南科技学院 土木与环境工程学院,湖南 永州 425199)

针对传统算法在反演概率积分法参数时易发散且难以获得全局最优解的问题，提出利用自适应人工蜂群算法反演概率积分法参数。根据该算法在求解过程中收敛速度快，获得全局最优解的特点，将参数反演问题转化为组合优化问题，建立了自适应人工蜂群算法的概率积分法预计参数反演流程，并将计算结果与实际值进行对比分析。通过理论分析与实验证明，自适应人工蜂群算法反演概率积分法参数精度高，较最小二乘法和模矢法拟合效果好，可应用于矿山开采沉陷预计。

开采沉陷；概率积分法；自适应人工蜂群算法；参数反演

基于随机介质理论的概率积分法因其理论基础坚实、易于计算机实现、应用效果好而在我国开采沉陷预计中广泛使用[1]。开采沉陷的预计精度与概率积分法参数有直接关系，因此，准确求取概率积分法参数对于提高开采沉陷预计精度很关键。目前，反演概率积分法分为直接反演[2]、实验设计方法反演到优化算法反演[3]、智能算法反演[4]。但直接反演法由于概率积分法函数的复杂性使其难以实现，且易发散；实验设计方法实验次数多，工作量大，难以实现反演软件化推广应用；优化算法对初值比较敏感，易陷入局部最优解；智能算法反演常用的是遗传算法，但是遗传算法的实现过程复杂，包括对问题进行编码和解码，而且局部搜索能力较差，容易造成早熟收敛等问题[5-6]。

针对以上方法反演概率积分法参数时存在的问题，提出将自适应人工蜂群算法(Self Adaptive Artificial Bee Colony，SAABC)引入开采沉陷预计参数反演中。人工蜂群算法(Artificial Bee Colony，ABC)是一种群集智能随机优化算法，具有原理简单、易于实现、控制参数少、鲁棒性强等特点[7]。本文首先将参数反演问题转化为组合优化问题，然后建立了基于自适应人工蜂群算法的概率积分法预计参数反演的具体流程，最后通过矿区沉降实例进行反演分析，并与最小二乘法和模矢法的拟合效果进行了比较。实验结果表明，自适应人工蜂群算法反演概率积分法预计参数精度高，证明了该方法的可行性和有效性。

1 人工蜂群算法

1.1 ABC算法简介

人工蜂群算法是土耳其学者Karaboga D提出的一种仿生智能寻优算法[8]，与粒子群算法、差分进化算法、进化算法等相似，本质都是统计优化算法，但其设置参数少，操作简单，鲁棒性高，收敛速度较快，收敛精度更高[9]。ABC算法模拟了蜜蜂的采蜜过程，通过蜂群的相互合作，转变指导搜索，在设定的参数空间中能够找到满足目标函数的最优解向量[10]。

人工蜂群算法中包括食物源、引领蜂和未雇佣蜂3个基本组成部分和两种主要的行为模式：蜜源招募蜂蜜和放弃食物源。食物源代表了优化问题解的位置，其价值用适应度来表示；引领蜂存储着某一食物源信息；非雇佣蜂负责探索和开采食物源，分为跟随蜂和侦察蜂。首先，由侦察蜂搜寻食物源，当食物源被找到之后，其返回蜂巢分享食物源的信息给其他蜂蜜，然后跟随蜂将选择某一侦察蜂找到的食物源，判断该食物源价值是否满足要求，若不满足则舍弃，此时引领蜂又会成为侦察蜂，重新寻找新的食物源，直到找到最优食物源[11]。模拟该行为的算法主要步骤如下：

1)初始化种群。根据参数范围随机产生一个原始种群。设初始解为N(N为蜜源数，也就是引领蜂和跟随蜂数)。每个解xi是一个D维的向量(D为待优化的参数个数)。

2) 引领蜂由式(1)产生新食物源，由式(2)比较当前食物源和新食物源的适应度值，以判断是否用新食物源代替当前食物源vi。

(1)

(2)

式中：j，k为随机选择的下标，k≠j；Φi,j为[-1，1]中的随机数;fi为目标函数；fit为适应度值。

3)跟随蜂依据各个蜜源的蜂蜜量来选择某一蜜源，概率选择公式如式(3)所示。同样通过贪婪选择原则选择适应度较好的作为新蜜源。

(3)

式中，pi为选择概率。

4)如果多次迭代之后引领蜂对应的食物源适应度值没有改进，则放弃当前食物源，相应的引领蜂变为侦查蜂，并由式(4)随机产生新食物源wi.j替换当前食物源。

(4)

式中，xi,j(min)，xi,j(max)分别为xi,j的下限和上限。

5)记录下目前最好食物源的适应度值及其位置。

6) 检查迭代次数是否达到终止条件，若满足终止条件，则结束程序，并输出其结果，否则执行步骤2)。

1.2 自适应人工蜂群算法

为了提高人工蜂群算法的收敛速度、运算时间、全局寻优等，很多学者提出了改进的方法。本文选用改进蜜源更新方式和跟随蜂选择引领蜂方式的人工蜂群算法，即自适应人工蜂群算法[12]。该算法是在标准人工蜂群算法的引领蜂和跟随蜂阶段，采用式(7)进行蜜源的更新，使算法能更好地跳出局部最优，提高后期搜索效率和优化性能；采用式(8)选择引领蜂，简化了算法复杂性，很大程度减少了运行时间。

(5)

(6)

(7)

(8)

式中：θi,j，μ1，μ2为随机数，Cycle为当前迭代次数，MaxCycles为最大循环次数，fit为第i位置蜜源的适应度，max(fit)为种群最大的适应度值。

在文献[13]中对SAABC算法进行了仿真实验，证明了此算法的寻优性能：收敛速度快，收敛精度高，能有效地跳出局部最优进而搜索到全局最优等。

2 自适应人工蜂群算法反演概率积分法参数步骤

2.1 问题描述

矿山开采下沉预计最常用的方法是概率积分法，其任意点M(x,y)的下沉预计模型为

(9)

其中：

(10)

(11)

(12)

(13)

(14)

(15)

(16)

式中：q为下沉系数，m为煤层厚度，α为煤层倾角，r为主要的影响半径且r=H/tanβ，β为主要影响角，H为采深，θ0为开采影响传播角。D1，D3分别为工作面倾向和走向长，s1，s2分别为下山和上山方向的拐点偏距，s3，s4分别为走向方向左边界和右边界的拐点偏距。

概率积分法预计参数主要包括：下沉系数q，水平移动系数b，主要影响角正切tanβ，开采影响传播角θ0，拐点偏移距s1，s2，s3，s4[14]。开采沉陷预计参数位移反分析就是求取概率积分法中参数，设p=[q,tanβ,s,θ0]，B为p的搜索空间(参数范围)，若地面点下沉测量值为wi，以误差平方和最小准则，则概率积分法参数的计算过程可表示为式(17)的约束优化问题，即在给定空间B中找到一个向量p0，使目标函数的值最小。

(17)

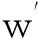
2.2 反演步骤

由2.1节可知,概率积分法参数反演就是在给定空间搜索一组解向量使目标函数值最小的组合优化问题。根据工作面上方覆岩岩性分类情况参照《规程》[15]规定设置参数p的寻优范围，由SAABC算法的原理可得基于自适应人工蜂群算法反演概率积分法参数的步骤为：①设置初始化种群数、最大循环次数等参数，根据参数p的范围生成初始种群。②计算适应度值，取适应度较优的一半为引领蜂，另一半则为跟随蜂。③引领蜂和跟随蜂分别产生新的种群并结合产生迭代种群。④计算迭代种群的适应度值并判断是否最优。如此循环直到找到最优食物源，即解向量，其具体实现流程如图1所示。

图1 自适应人工蜂群算法计算概率积分法参数流程

3 实例分析

选取钱营孜煤矿3212工作面为例，其走向长2 224 m，倾向长200 m，平均采厚3.01 m，平均开采深度661 m，煤层平均倾角为16°，覆岩岩性为中硬，煤层走向为NW。3212工作面直接揭露的断层有3个，断点34处，煤层直接顶板以灰黑色泥岩为主，工作面直接顶较软弱，局部有深灰色粉砂岩，平均厚约2.17 m；局部地段会出现伪顶泥岩，厚约0.1～0.5 m左右；区内煤系地层被第三、四系新生界松散层覆盖，松散层厚192.05～249.60 m，平均厚224.58 m，矿井总体属厚松散层，大采深地质采矿条件。在该工作面上建立了2条观测线。其中在工作面上方切眼端沿走向方向主断面布置1条半走向观测线；在工作面倾向方向近主断面上设置1条倾向观测线。

根据2.2的反演流程，在煤层上方沿走向线和倾向线共选取60个观测点，在设计算法时，根据SAABC的原理反复变换参数，经过调试分析，确定本次实验算法参数为：初始种群数为80，最大循环次数为1 500。通过获得的概率积分法参数得到该工作面地表下沉拟合曲面如图2所示，从图中可以看出拟合效果较好，能够反映地表沉陷状况，沉陷规律符合概率积分模型。

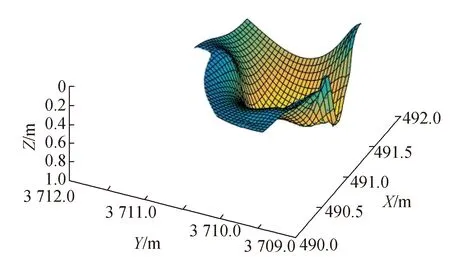
图2 预计下沉曲面

利用人工蜂群算法预计的下沉值与实测值的对比如图3所示。从图中可以看到大部分测点预计值与实测值比较接近，误差较小，证明了人工蜂群算法在反演概率积分法参数时的可行性和有效性。但从图3中可以看到测点10处实测下沉值较大，而且预计值与实测值相差较大，其原因是测点10离断层较近，受断层的影响下沉值增大，改变沉陷影响范围，此时应用常规的概率积分法预计误差较大[16]。图3中测点30至40的区域预计值小于实测值，误差较大，是因为此区域存在较厚的松散层所致，在厚松散层的影响下，开采引起的地表沉陷范围增大[17]。

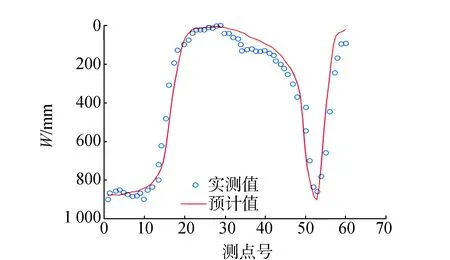
图3 下沉预计值与实测值对比

在相同的条件下，分别利用最小二乘法和模矢法计算参数，并计算出各观测线下沉值拟合中误差，3种算法的拟合中误差对比结果如表1所示，从表中可以看出自适应人工蜂群算法拟合效果优于最小二乘法和模矢法，说明自适应人工蜂群算法能有效应用于开采沉陷预计参数求取问题。

表1 观测线下沉值拟合中误差对比

4 结束语

传统方法在求取概率积分法参数时易发散且难以获得全局最优解，因此，本文提出利用自适应人工蜂群算法反演概率积分法参数。自适应人工蜂群算法控制参数少，自适应性强，能有效跳出局部最优解进而搜索到全局最优解。实验表明，采用自适应人工蜂群算法反演概率积分法参数准确可靠，较最小二乘法和模矢法拟合效果好，可用于矿山开采沉陷预计。

[1] 朱晓峻,郭广礼,方齐.概率积分法预计参数反演方法研究进展[J].金属矿山,2015,44(4):173-177.

[2] 郭广礼,汪云甲.概率积分法参数的稳健估计模型及其应用研究[J].测绘学报,2000,29(2):162-165.

[3] 葛家新.地表沉陷预计参数求取及其分析[J].矿山压力与顶板管理,2004,21(1):78-79.

[4] 于宁锋,杨化超.基于粒子群优化神经网络的概率积分法预计参数的确定[J].测绘科学,2008,33(2):78-80.

[5] 冯夏庭,王泳嘉.采矿智能系统—人工智能与神经网 络在矿业工程中的应用[M].北京:冶金工业出版 社,1994.

[6] 孙豁然,王述红,宫永军，等.大型地下硐室开挖过程位移变形智能预测[J].煤炭学报,2001,26(1):45-48.

[7] 史明霞,陶林波,沈建京.自适应遗传算法的改进与应用[J].微计算机应用,2006,27(4):405-408.

[8] 王春颖.自适应的人工蜂群算法[D].长春：东北师范大学,2012.

[9] KARABOGA D.An idea based on honey bee swarm for numerical optimization,Technical Report-TR06[R].Erciyes University,2005

[10] 王艳娇.人工蜂群算法的研究与应用[D].哈尔滨：哈尔滨工程大学,2013.

[11] TSAI P W,PAN J S,LIAO Y B,et al.Enhance artificial bee colony.The International Journal[J].of Innovative Computing,Information and Control,2009,5 (12):1-12.

[12] KARABOGA D,BASTURK B.On The Performance Of Artificial Bee Colony (ABC) Algorithm [J].Applied Soft Computing,2008,8(1)：687-697.

[13] 何鹏.人工蜂群算法研究[D].上海：华东理工大学,2014.

[14] 何国清,杨伦,凌赓娣.矿山开采沉陷学[M].江苏徐州:中国矿业大学出版社,1991.

[15] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000.

[16] 吴侃,蔡来良,陈冉丽.断层影响下开采沉陷预计研究[J].湖南科技大学学报(自然科学版),2008,23(4):10-13.

[17] 顾伟.厚松散层下开采覆岩及地表移动规律研究[D].北京：中国矿业大学,2013.

[责任编辑：刘文霞]

Parameters inversion in probability integral method based on self-adaptive artificial bee colony

LIU Qi1，ZHU Jianjun1， SU Junming1,2，HE Yonghong1,3，SUN Mingxing1

(1.School of Geosciences and Info-Physics，Central South University，Changsha 410083，China;2.Zhongnan Engineering Corporation Ltd., Changsha 410014, China;3. School of Civil and Environmental Engineering, Hunan University of Science and Engineering, Yongzhou 425199, China)

As to the problems of divergence and difficulty in optimum acquisition,a self-adaptive artificial bee colony is applied to estimating the parameters of probability integral method. It has the features of rapid convergence and achieving the global minimum. The parameter inversion problem is transformed into combination optimization problem, and then the flow of calculation parameters inversion of aim-listed probability integral method-based on the self-adaptive artificial bee colony is established. The calculated results are compared with the actual values.The result shows that the parameters of probability integral method can be precisely inversed. The fitting effect is better than least square method and pattern search method. It proves that this algorithm can be applied to the prediction of coal mining subsidence.

mining subsidence; probability integral method; self-adaptive artificial bee colony; parametric inversion

著录：刘奇，朱建军，苏军明，等.基于改进人工蜂群算法的概率积分法参数反演[J].测绘工程，2017，26(10)：18-21，29.

10.19349/j.cnki.issn1006-7949.2017.10.004

2016-09-05

国家自然科学基金资助项目(41531068；41274010；41371335)；国家973计划资助项目(2013CB733303)；国家863计划资助项目(2012AA121301)；湖南省研究生科研创新项目(150140004)；湖南省自然科学基金资助项目(14JJ2131)；中南大学中央高校基本科研业务费专项资金资助项目(2016zzts083)

刘 奇(1991-)，男，硕士研究生.

TD325

A

1006-7949(2017)10-0018-04